Решение систем линейных уравнений

1. Решение систем линейных уравнений.

УЧИТЕЛЬ : БУЛГАКОВА О.А.
МАОУ СОШ №31 Г. ТАМБОВ

2. Цель: Закрепить решение систем линейных уравнений и решение задач с помощью системы линейных уравнений.

Задачи:
Повторить решение систем графическим способом.
Закрепить решение систем методом подстановки и
методом сложения.
Продолжить развивать математическое мышление,
логику, речь.
Продолжить показывать применение математики в
других областях знаний .
Воспитывать любовь к своей малой родине.

3.

Крупное научное открытие дает
решение крупной проблемы, но и в
решении любой задачи
присутствует крупица открытия .
Двёрдь Пойа

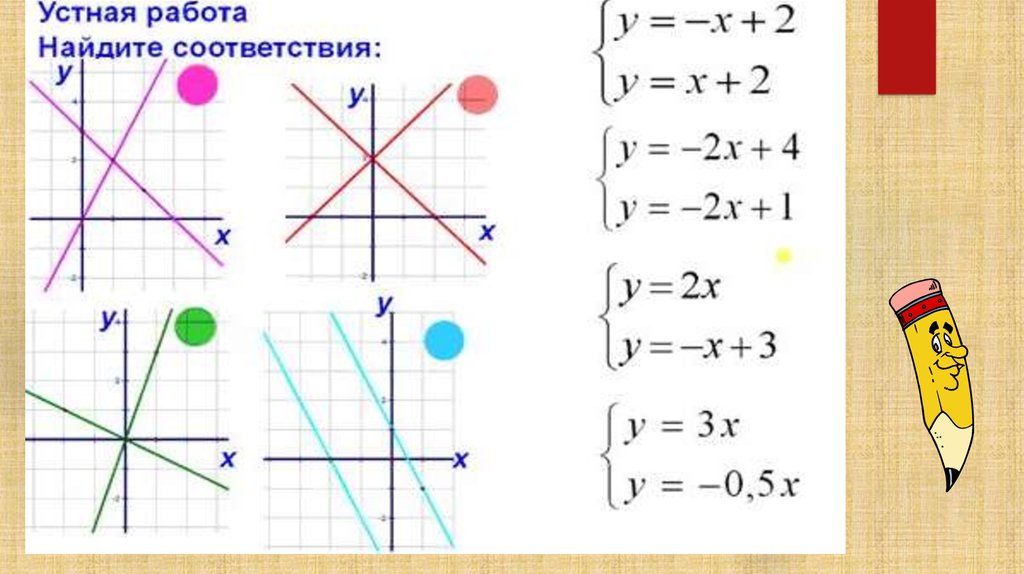
4. Из каких уравнений можно составить систему, решением которой будет пара чисел (1;0)

А. 5х+у=8
В. 2х-3у=2
Б. 4х+у=4
Г. 6х+5у=1
4х+у=4
ቊ
2х−3у=2.

5.

6. Алгоритм решения системы методом подстановки.

1. Из одного уравнения выражают одну
переменную через другую;
2. Подставляют во второе уравнение
найденное выражение;
3. Решают полученное уравнение с одной
переменной;
4. Находят соответствующее значение
другой переменной;
5. Записывают ответ.

7. Алгоритм решения системы методом сложения.

1. Уравнять модули коэффициентов при какой нибудь переменной
2. Сложить (вычесть) почленно уравнения систем.
3. Решить уравнение с одной переменной.
4. Подставить значение найденной переменной в
одно из исходных уравнение и найти значение
другой переменной
5. Записать ответ.

8. Решите системы уравнений методом подстановки.

(3;20)
(20;2)
М
О
(4;2)
(5;6)
(6;4)
Р
Ш
А
(-3;-2)
(2;3)
(3;-2)
Н
С
К

9. Решите системы уравнений рациональным методом.

(-2;1)
Р
(3;1)
А
(3;-2)
С
(2;3)
С
(-3;-2)
К
(6;4)
А
(5;6)
З
(4;2)
О
(20;2)
В
(3;-20)
О

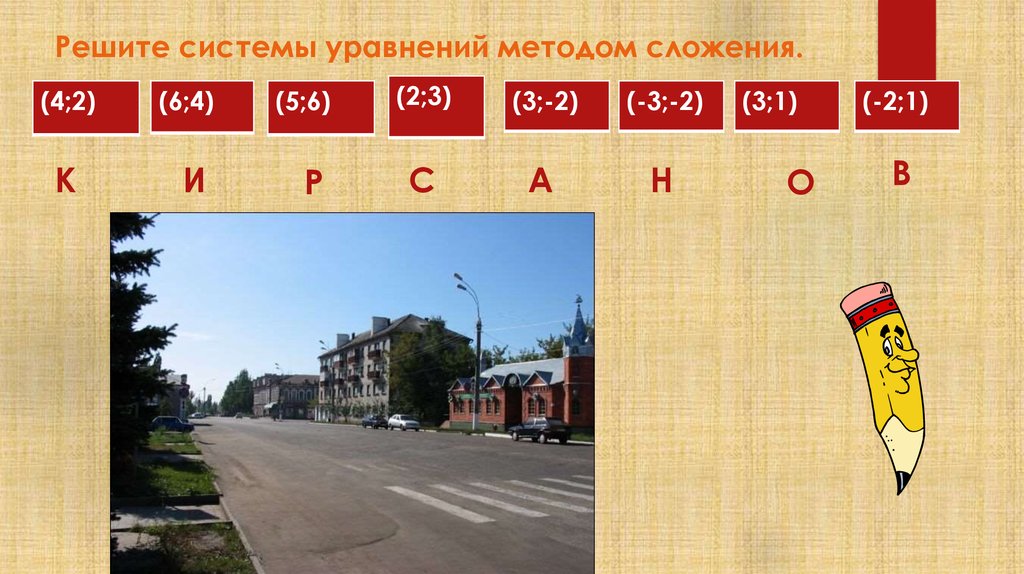
10. Решите системы уравнений методом сложения.

(4;2)
К
(6;4)
И
(5;6)
Р
(2;3)
(3;-2)
(-3;-2)
С
А
Н
(3;1)
О
(-2;1)
В

11. Решите задачу, используя для составления математической модели две переменные.

Город Мичуринск построен на
один год раньше города
Тамбова. Если сложить их
возраст то получится 755 лет.
Каков возраст городов Тамбова и
Мичуринска?

12. Решите задачу, используя для составления математической модели две переменные.

Площадь города Тамбова в
4,2раза больше площади
города Уварова тамбовской
области. Найдите площади
этих городов, если площадь
г. Уварова на 69,44 км2
меньше площади
г. Тамбова.

13. Решите задачу, используя для составления математической модели две переменные.

Путь от г. Тамбова до
г. Мичуринска по железной
дороге на 66км длиннее, чем
по шоссе .
Поезд проходит этот путь за
1час 15минут, а автомобиль
за 1час 12минут. Найдите
среднюю скорость поезда и
автомобиля, если известно,
что скорость автомобиля