Similar presentations:
Конкурсное задание «УРОК»
1.
Конкурсное задание«УРОК»
Учитель –
Комарова Светлана Эриевна,
МОУ «Усогорская СОШ с УИОП»
28 февраля 2018 года
2.
3.
4.
Производные тригонометрических функций(sin x)ˊ = cos x
(cos x)ˊ = ̶ sin x
5.
Дома: стр.333, вывод формулыпроизводной функции f(x) = sin x
6.
Жозеф ЛуиЛАГРАНЖ
1736 – 1813
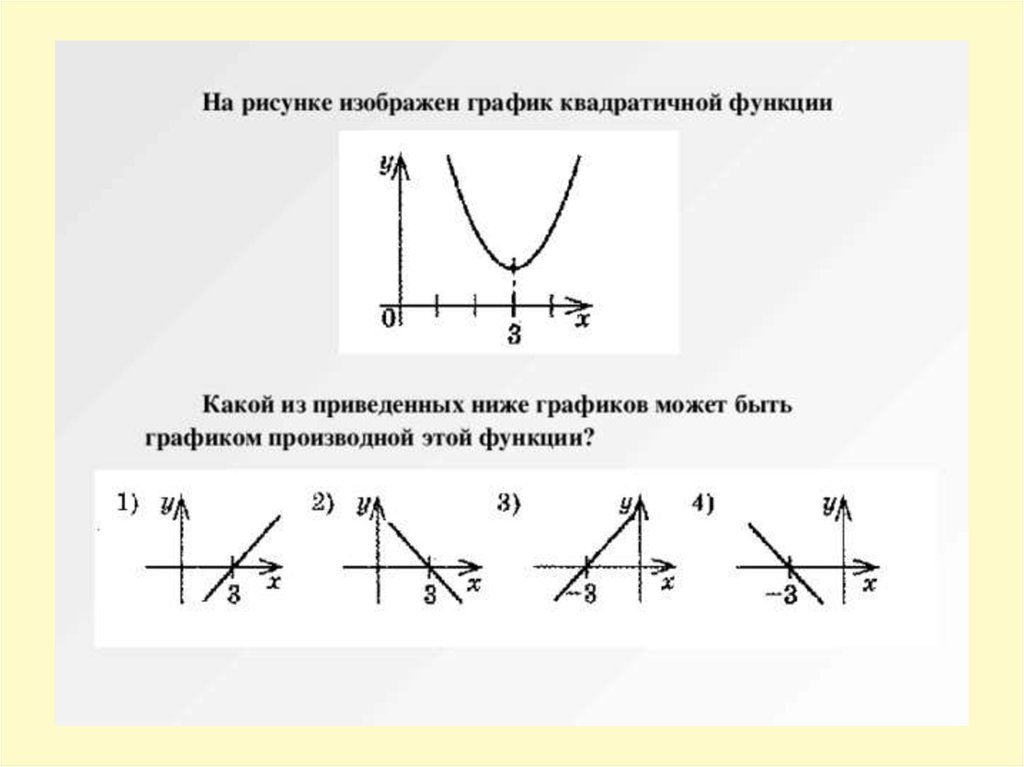
f ˊ(x)
«Я сделал своё дело… Я
никогда никого не ненавидел, и
не делал никому зла»
7.
(sin ( 2x + 1))ˊ = ?8.
Сложная функция2х + 1
(2х + 1)3
3
sin (2х + 1)
9.
Производная сложной функции(f (g(x)))ˊ = f ˊ(g(x))· (g(x))ˊ
(sin (2x + 1))ˊ =
= (cos (2x + 1)) · ( 2x + 1)ˊ =
= 2 cos (2x + 1)
10.
f(x) = 3-2x fˊ(x) = -22
gˊ(x) = 2x
g(x) = x
p(x) = sin x pˊ(x) = cos x
f(p(x) )= 3-2sin x
p(f(x)) = sin (3-2x)
2
p(g(x) )= sin (x )
g(p(x)) = (sin x) 2
11.
(f (p(x)))ˊ= (3-2sin x)ˊ= -2cos x(p (f(x)))ˊ= (sin (3-2x))ˊ=
= -2cos (3-2x)
(p(g(x)))ˊ= (sin
2
2
(x ))ˊ=2x·cosx
(g(p(x)))ˊ= ((sin x)2)ˊ=
=2sin x ·cos x
12.
Найдите производные функций:ˊ
(sin (4-5x))ˊ= - 5 cos (4-5x)
(cos (6x +
(
))ˊ= - 6 sin (6x + )
cos (2-8x))ˊ= 2 sin (2-8x)
(sin
2x
+
2
cos x)ˊ=
0
(2 sin ( - x))ˊ= - 2 sin x
13.
Самостоятельная работаНайдите производные функций:
ВАРИАНТ 1
ВАРИАНТ 2
1). (sin (2-3x))ˊ=
2). (cos (5x + 2))ˊ=
1). (sin (3+4x))ˊ=
2). (cos (7x - 3))ˊ=
3). ( sin (12x + 6))ˊ=
3). ( cos (15x - 2))ˊ=
4). (4 cos (x - ))ˊ=
4). (3 sin (x + ))ˊ=
5). (-2 sin (3x +
))ˊ=
5). (-4 cos (2x -
))ˊ=
14.
Ответы к самостоятельной работеВАРИАНТ 1
ВАРИАНТ 2
1). - 3 соs (2-3x)
1). 4 cos (3 + 4x)
2). – 5 sin (5x + 2)
2). -7 sin (7x – 3)
3). 2 cos (12x + 6)
3). – 3 sin (15x – 2)
4). – 4 sin (x -
4). 3 cos (x + )
5). - 6 cos (3x +
)
)
5). 8 sin (2x -
)
15.
Домашнее задание:1) стр.333, вывод
формулы производной
функции f(x) = sin x
2) № 42.2
16.
Производные тригонометрическихи сложных функций
Что узнали на уроке?
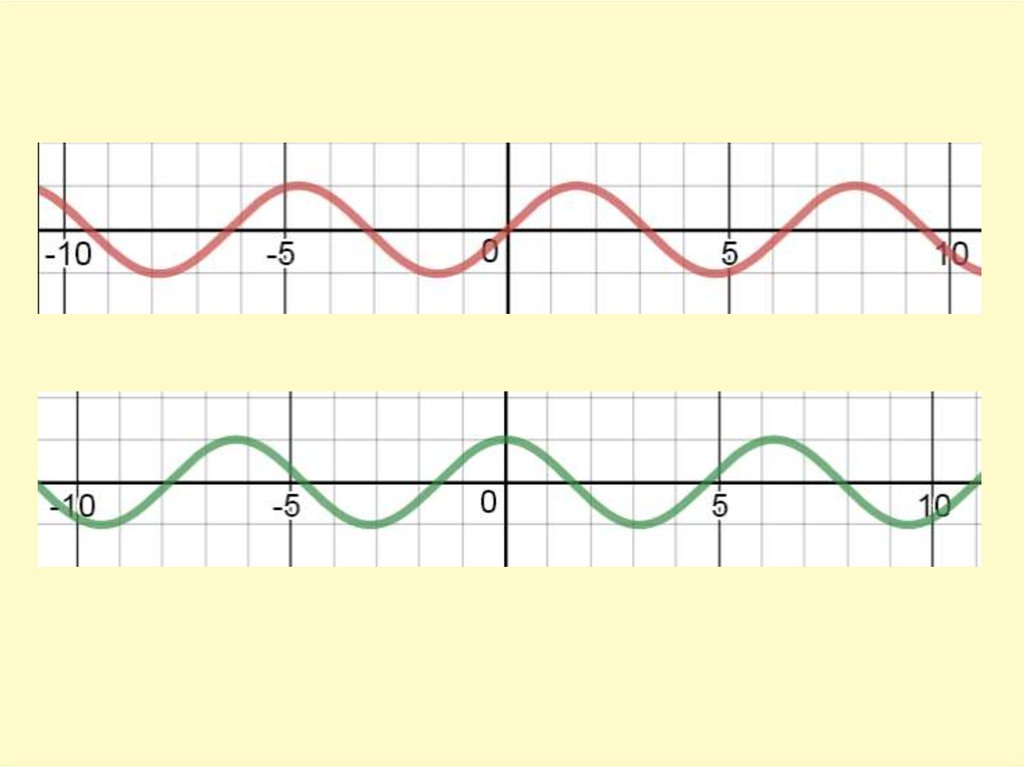
(sin x)ˊ = cos x
(cos x)ˊ = ̶ sin x
(f (g(x)))ˊ = f ˊ(g(x))· (g(x))ˊ
Чему научились?





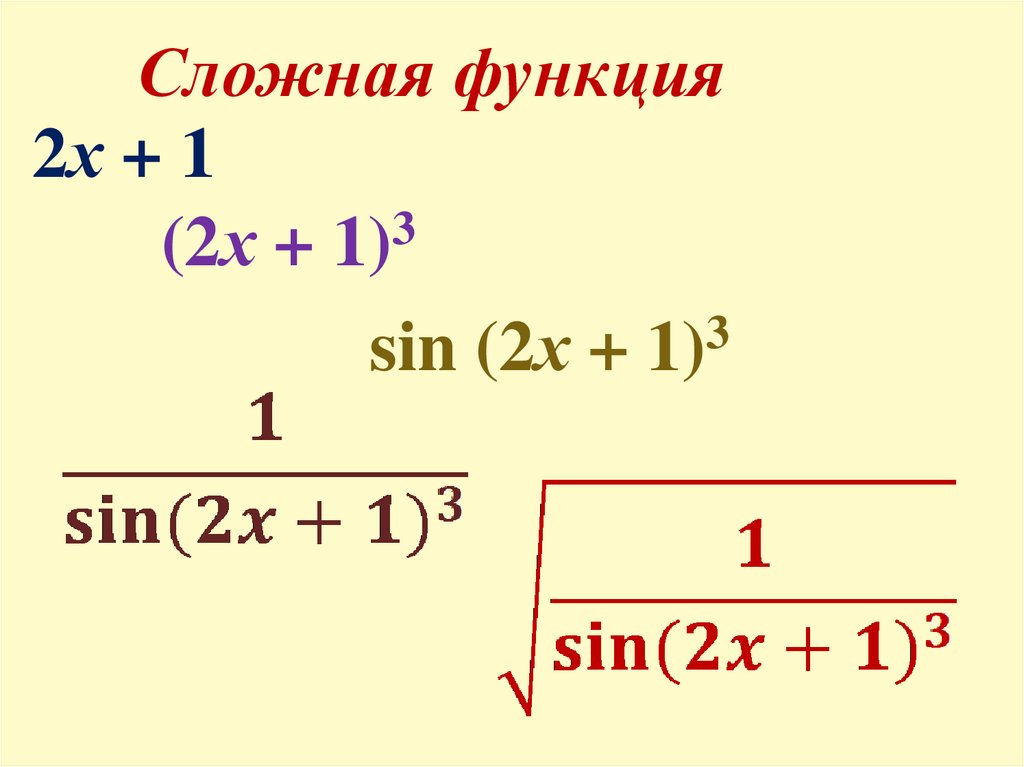

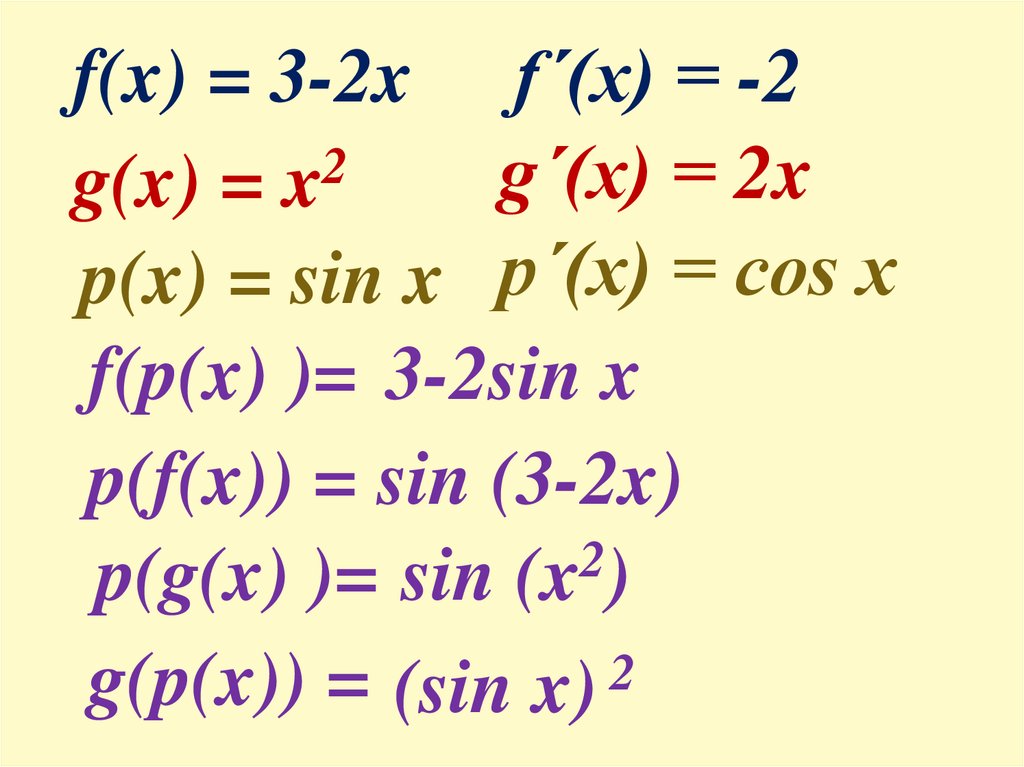
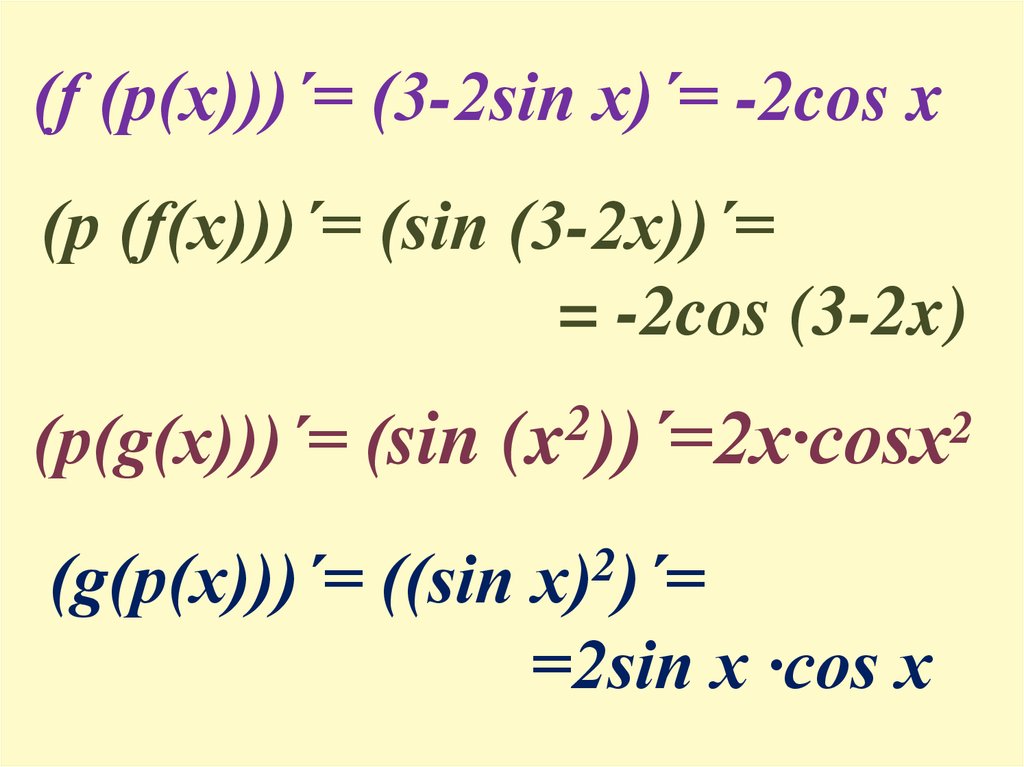





 mathematics
mathematics








