Решение простейших тригонометрических уравнений

1. Решение простейших тригонометрических уравнений

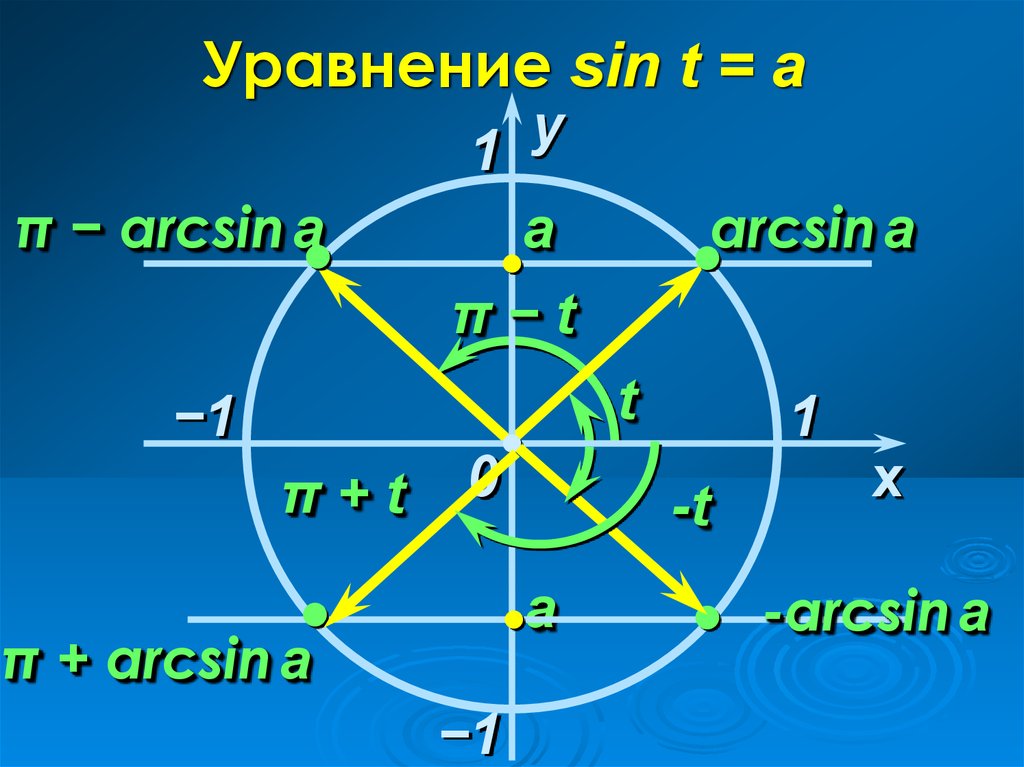
2. Уравнение sin t = а

π − arcsin a
у
1
а
arcsin a
π−t
t
−1
π+t
0
-t
а
π + arcsin a
−1
1
x
-arcsin a

3.

4.

Общее решения
данного уравнения
sin t = а
C учетом периодичности:
t = arcsin a + 2πn, n Z
t = π − arcsin a + 2πn, n Z
Объединив в одну формулу:
t = (−1)n arcsin a + πn, n Z

5.

√3
Пример 1 sin x = − 2
√3
x=
arcsin −
+ πn, n Z
2
√3
n+1
x = (−1) arcsin
+ πn, n Z
2
π
n+1
x = (−1)
+ πn, n Z
3
π
n+1
Ответ: (−1)
+ πn, n Z
3
(−1)n

6.

1 частный случай
y
1
−1
π
sin t = 0
1
0
x
0
t = πn, n Z
−1

7.

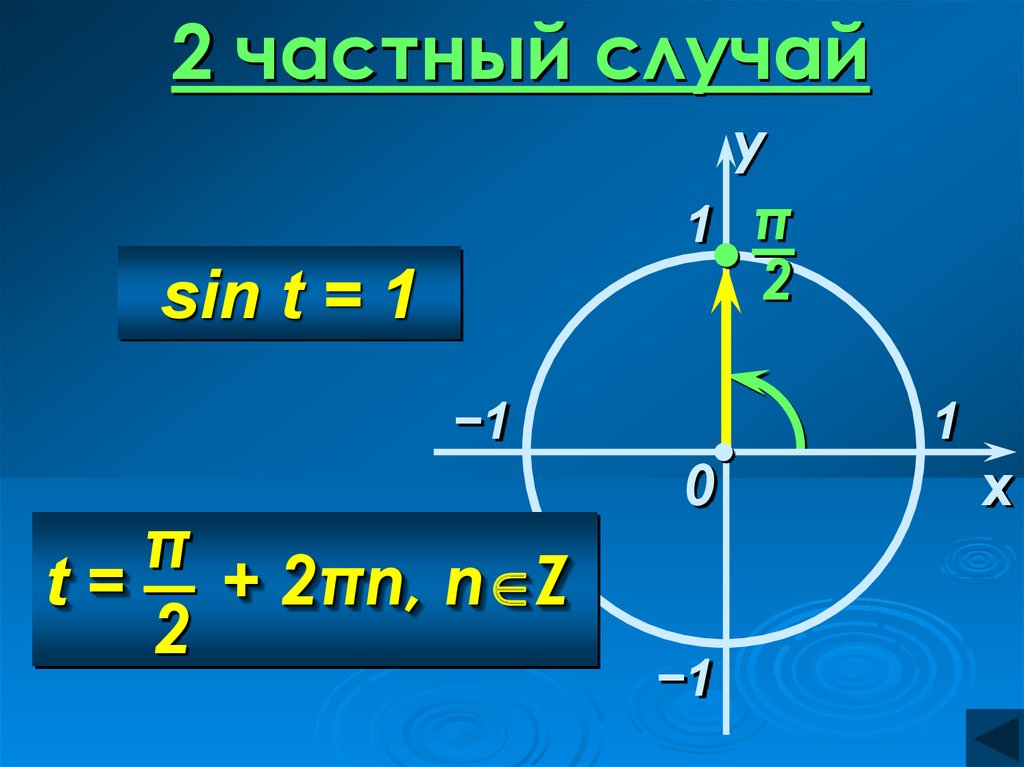
2 частный случай
y
1 π
2
sin t = 1
−1
π
t = + 2πn, n Z
2
0
−1
1
x

8.

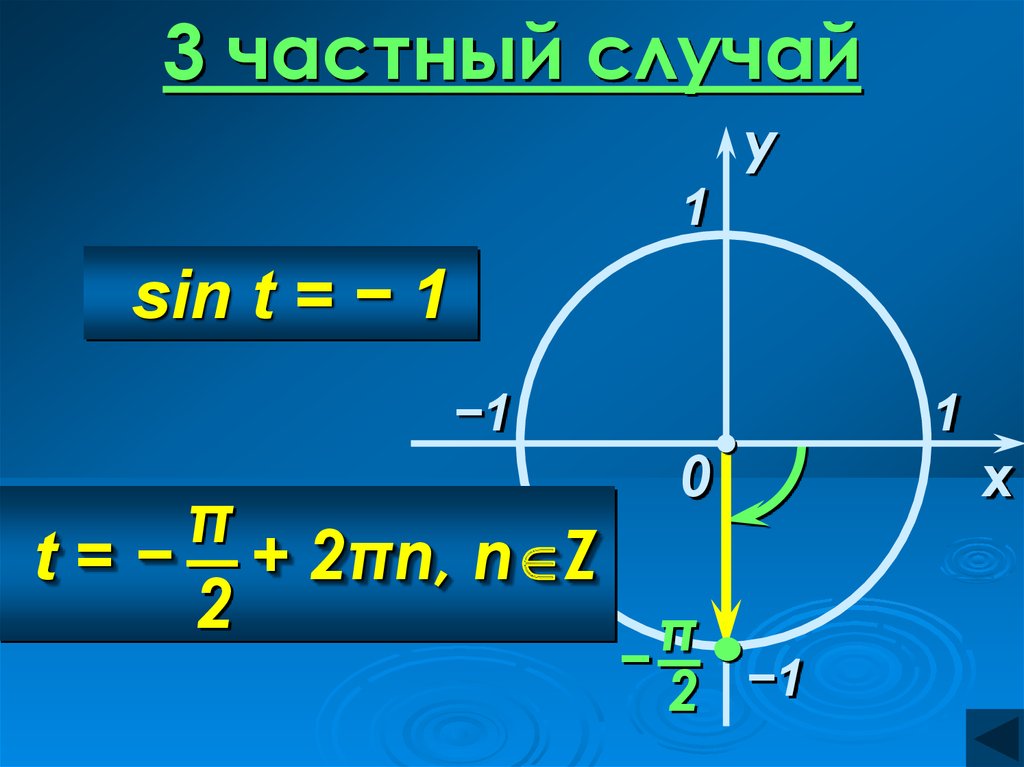
3 частный случай
y
1
sin t = − 1
−1
0
π
t = − + 2πn, n Z
−1 2
−1
π
−
2 −1
1
x

9. Уравнение cos t = а

у
1
arccos a
t
−1
0
−t
а
1 x
− arccos a
−1

10.

Общее решения
данного уравнения
cos t = а
C учетом периодичности:
t = arccos a + 2πn, n Z
t = − arccos a + 2πn, n Z
Объединив в одну формулу:
t= −
arccos
a
+
2πn,
n Z
+

11.

1
Пример 2 cos x =
2
x =+
−
x=+
−
1
arccos 2 + 2πn, n Z
π
+ 2πn, n Z
3
Ответ:
π
+ + 2πn, n Z
−3

12.

1 частный случай
y
π 1
2
cos t = 0
x
−1
0
π
−
2 −1
1
π
t = + πn, n Z
2

13.

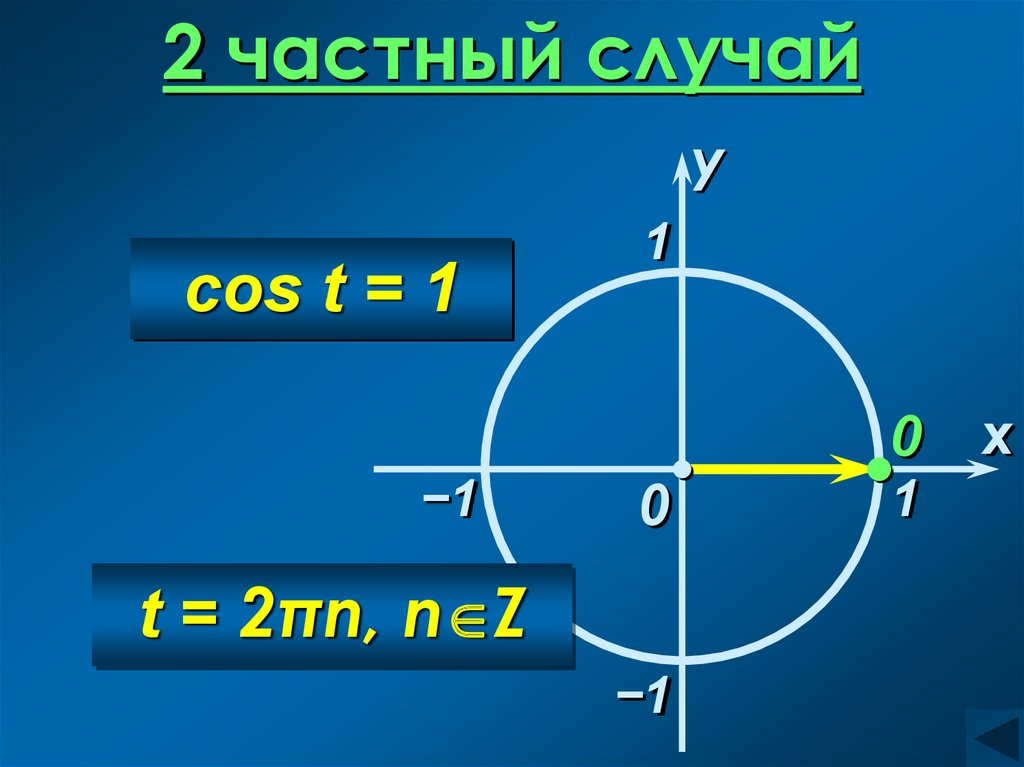
2 частный случай
y
cos t = 1
−1
1
0
t = 2πn, n Z
−1
0
1
x

14.

3 частный случай
y
1
π
−1
cos t = − 1
x
0
1
t = π + 2πn, n Z
−1