Similar presentations:
Производная и ее геометрический смысл. Урок обобщения и систематизации знаний
1. ПРОИЗВОДНАЯ И ЕЕ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Урок обобщения исистематизации знаний
учитель Валентина Васильевна Николаева
2. Проверка знаний фактического материала теории:
что такое производная?какая функция называется дифференцируемой в точке x0?
что значит продифференцировать?
какой смысл имеет производная с механической точки зрения?
какой смысл имеет производная с геометрической точки
зрения?
какой угол образует прямая с осью абсцисс:
если k>0
если k<0
если k=0
какую формулу имеет уравнение касательной?
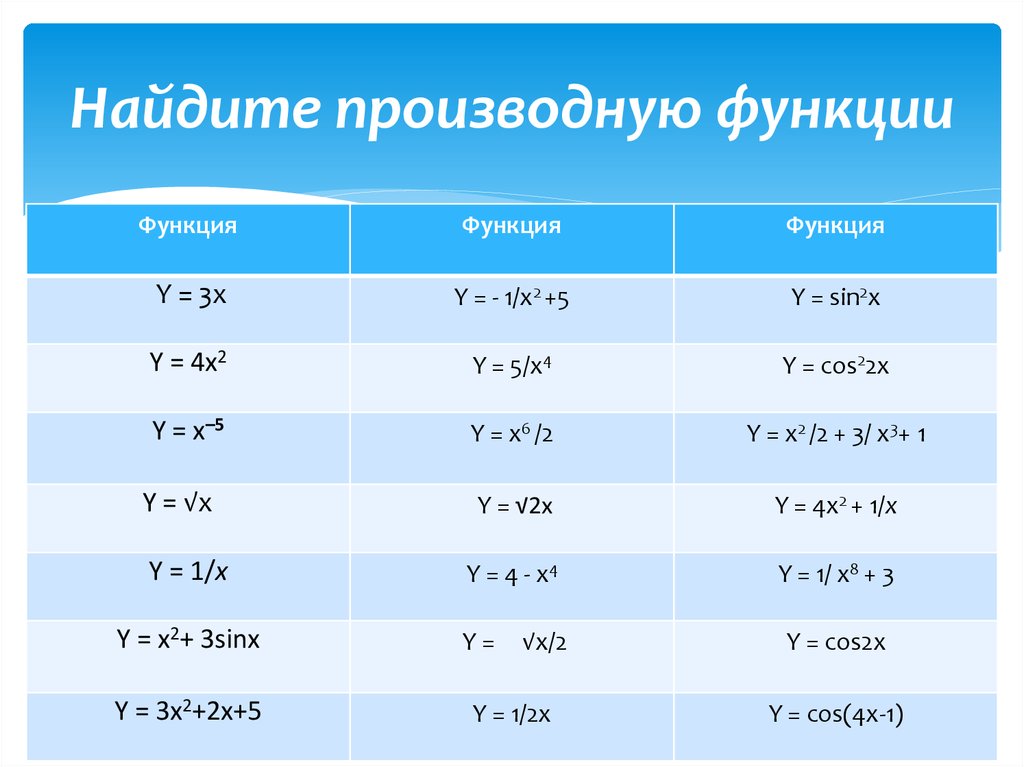
3. Найдите производную функции
ФункцияФункция
Функция
Y = 3x
Y = - 1/x2 +5
Y = sin2x
Y = 4x2
Y = 5/x4
Y = cos22x
Y = x–5
Y = x6 /2
Y = x2 /2 + 3/ x3+ 1
Y = √2х
Y = 4x2 + 1/х
Y = 4 - x4
Y = 1/ x8 + 3
Y = √х
Y = 1/х
Y = x2+ 3sinx
Y = 3x2+2x+5
Y=
√х/2
Y = 1/2x
Y = cos2x
Y = cos(4x-1)
4. Геометрический смысл производной
Найдите угловой коэффициенткасательной, проведенной к параболе
y = x2 - 7x + 10 в точке с абсциссой x0 = 4.
Найдите тангенс угла наклона касательной,
проведенной к графику функции y = 6x - 2/x в
точке с абсциссой x0 = - 1.
Найдите угол ( в градусах), образованный осью
ОX и касательной к графику функции
y = 3ex - 4x в точке x0 = 4.
5. Механический смысл производной:
Тело движется по прямой так, чторасстояние S (в метрах) от него до данной
точки М этой прямой изменяется по закону
S(t) = 2t3 - 3 t + 4 (t – время движения в секундах).
Найти скорость и ускорение в момент t = 2c.
6. ДОМАШНЕЕ ЗАДАНИЕ
глава Vlll№№ 877,878
"Проверь себя", стр. 258





 mathematics
mathematics








