Similar presentations:
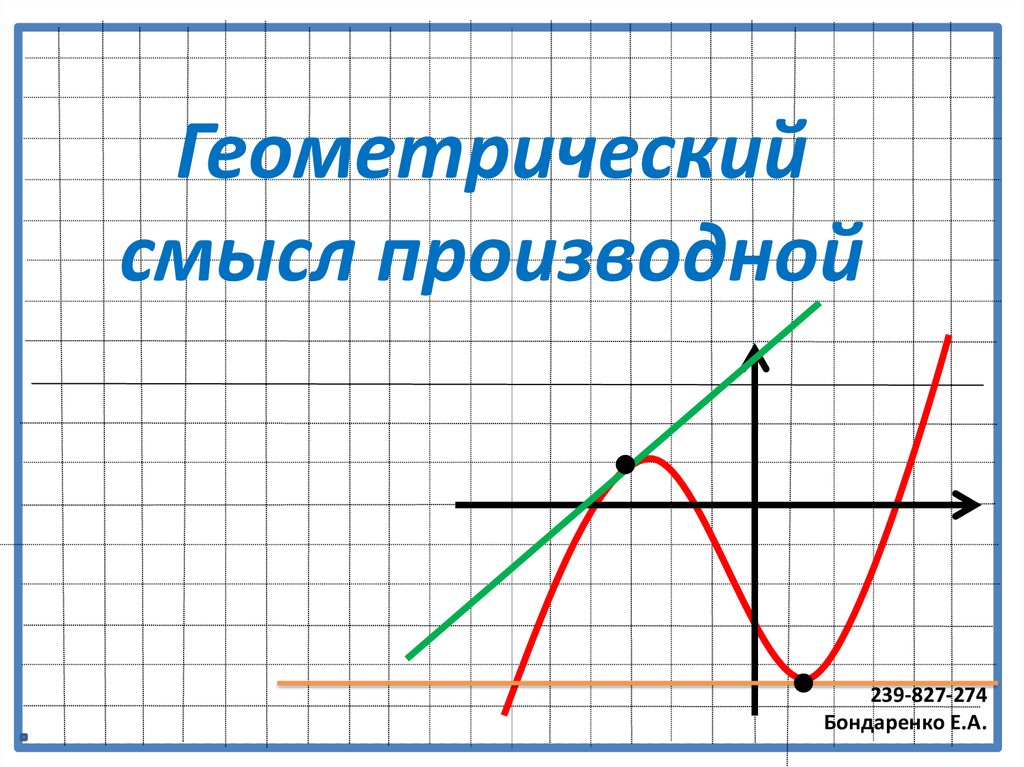
Геометрический смысл производной
1.
Геометрическийсмысл производной
239-827-274
Бондаренко Е.А.
2.
Рано или поздно всякая правильнаяматематическая идея находит
применение в том или ином деле.
А.Н.Крылов
3. Цель урока
1) выяснить, в чем состоит геометрический смыслпроизводной, вывести уравнения касательной к
графику функции
2) Развивать ОУУН мыслительной деятельности:
анализ, обобщение и систематизация, логическое
мышление, сознательное восприятие учебного
материала
3) формировать умение оценивать свой уровень
знаний и стремление его повышать,
способствовать развитию потребности к
самообразованию. Воспитание ответственности,
коллективизма.
4. Словарь урока
производная, линейная функция,
угловой коэффициент,
непрерывность, тангенсы углов
(острый, тупой).
5.
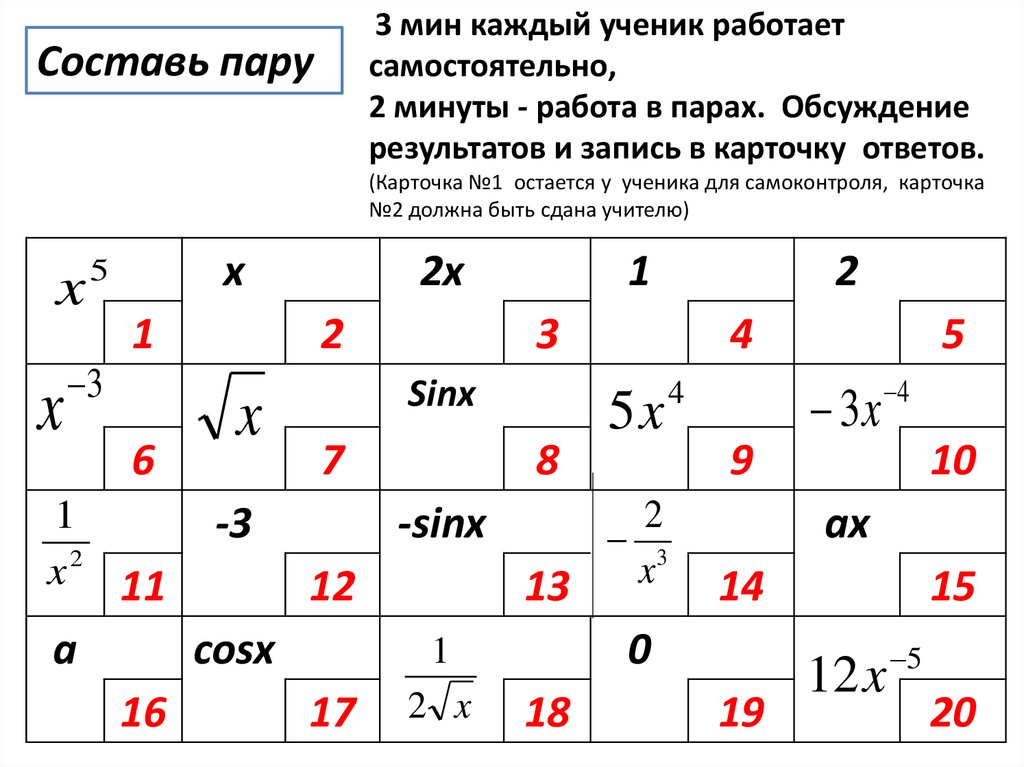
3 мин каждый ученик работаетсамостоятельно,
2 минуты - работа в парах. Обсуждение
результатов и запись в карточку ответов.
Составь пару
(Карточка №1 остается у ученика для самоконтроля, карточка
№2 должна быть сдана учителю)
x
x
х
5
3
1
6
1
x 2 11
a
2х
2
x
7
-3
8
-sinx
12
2 x
4
5x
2
3
13 x
18
5
3x
4
4
9
10
ax
14
0
1
17
2
3
Sinх
cosx
16
1
19
15
12 x
5
20
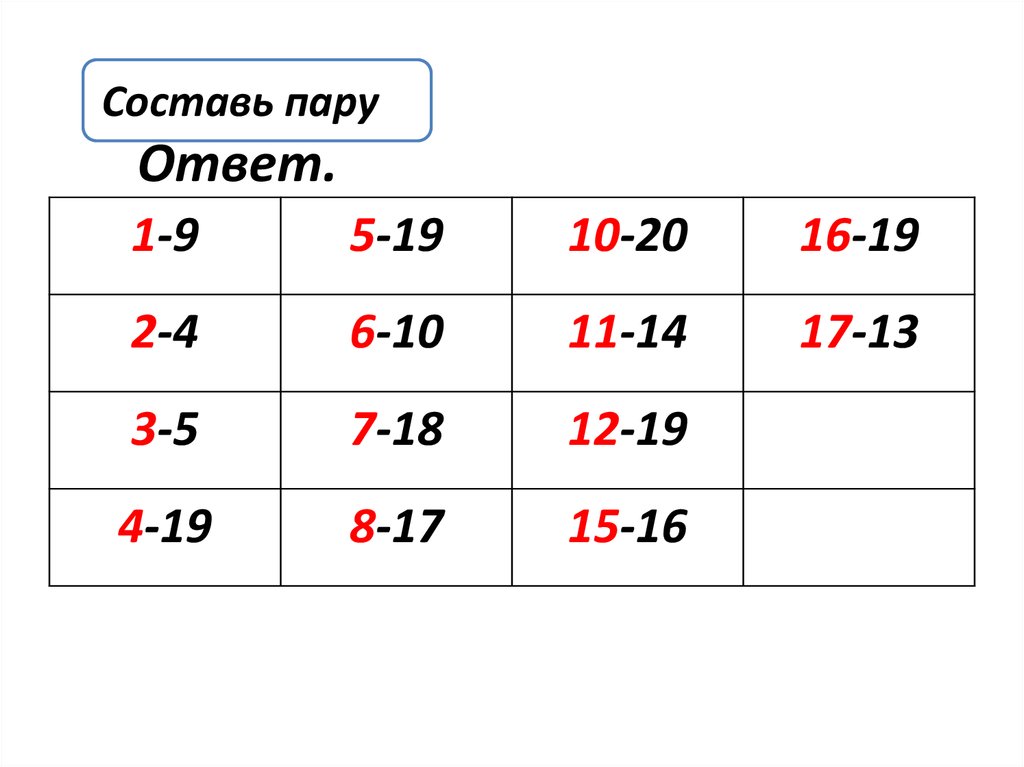
6. Ответ.
Составь паруОтвет.
1-9
5-19
10-20
16-19
2-4
6-10
11-14
17-13
3-5
7-18
12-19
4-19
8-17
15-16
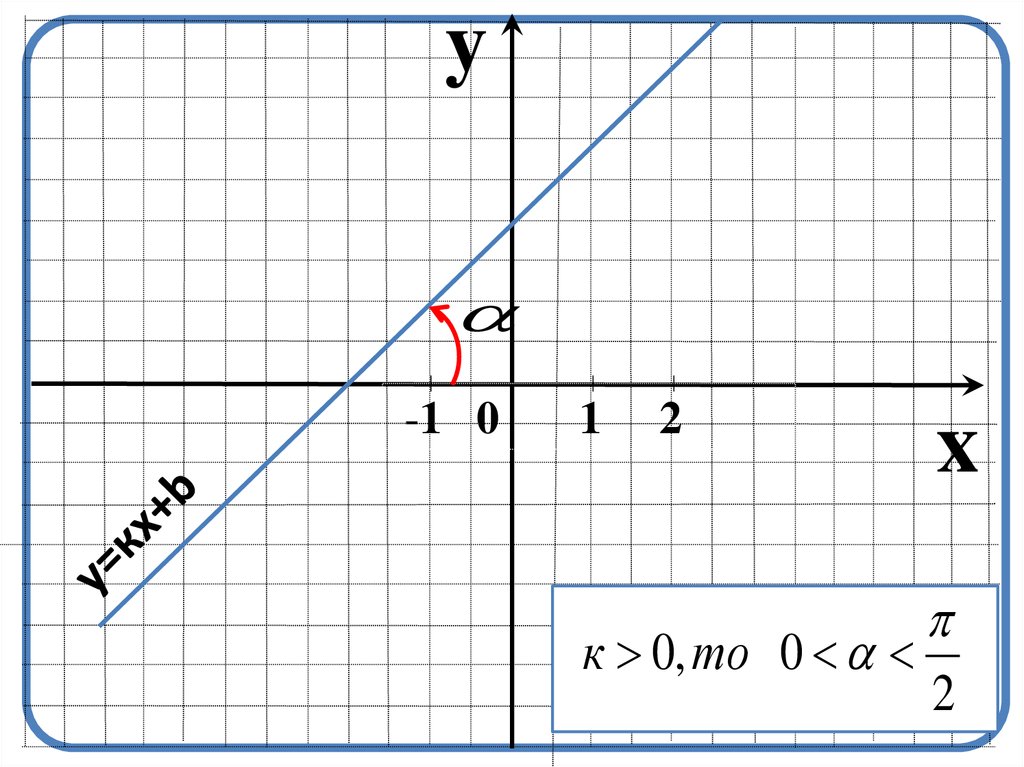
7. Определение
Функция заданная с помощьюформулы у=кх+b называется
линейной.
Число k=tg называется угловым
коэффициентом прямой.
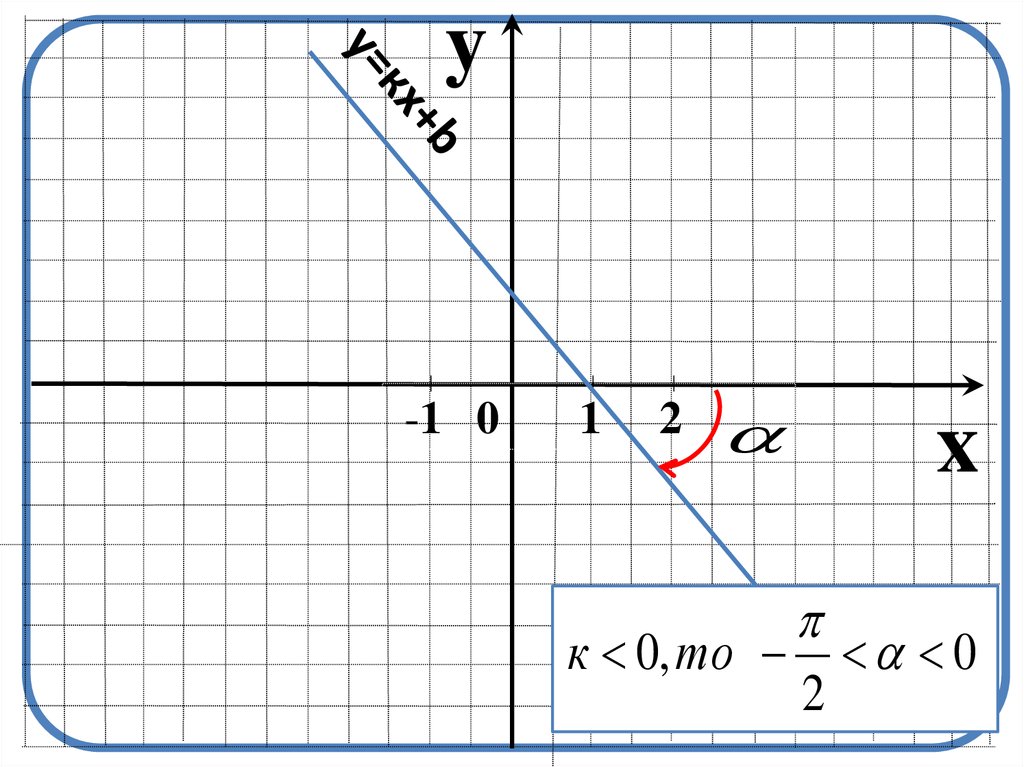
8.
y-1 0
1
2
x
к 0, то 0
2
9.
y-1 0
1
2
x
к 0, то 0
2
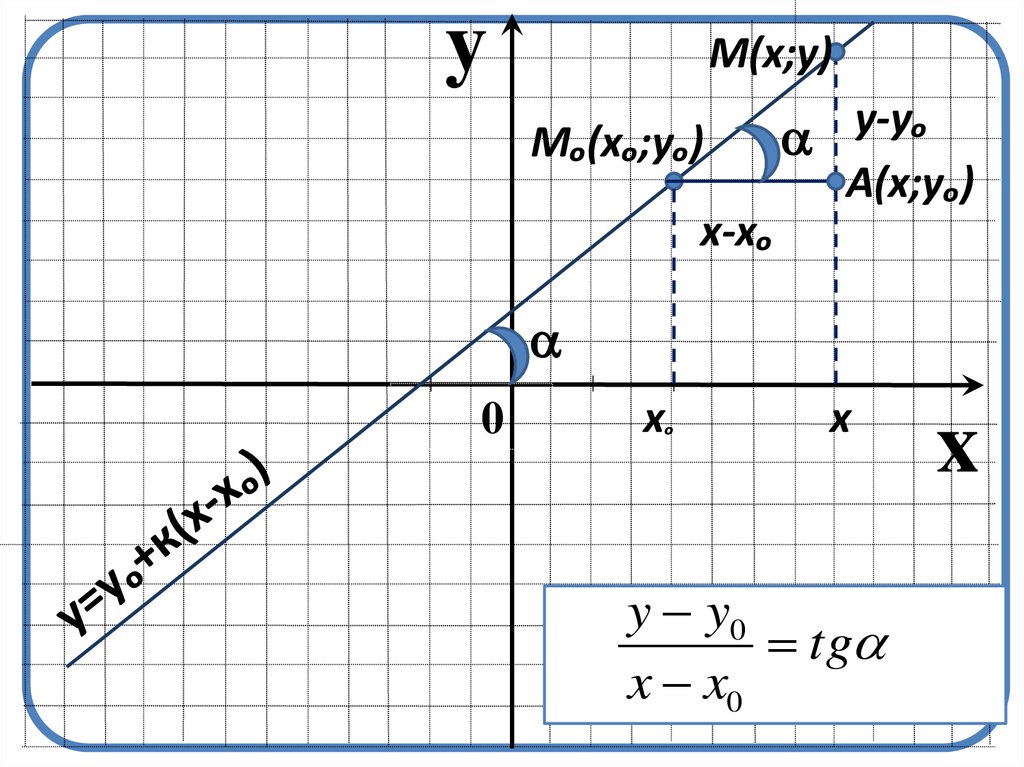
10.
yM(x;y)
Mₒ(xₒ;yₒ)
y-yₒ
A(x;yₒ)
x-xₒ
0
xₒ
x
y y0
tg
x x0
x
11.
Уравнение прямой с угловымкоэффициентом k, проходящей
через точку
(х с угловым
;у0)
Уравнение прямой 0
коэффициентом k, проходящей через точку
у=у0+k(x-x0) (1)
(х ;у )
0
0
у=у0+k(x-x0)
Угловой коэффициент прямой
проходящий через точки (х1;у1) и (х0;у0)
y1 y0
k
x1 x0
(2)
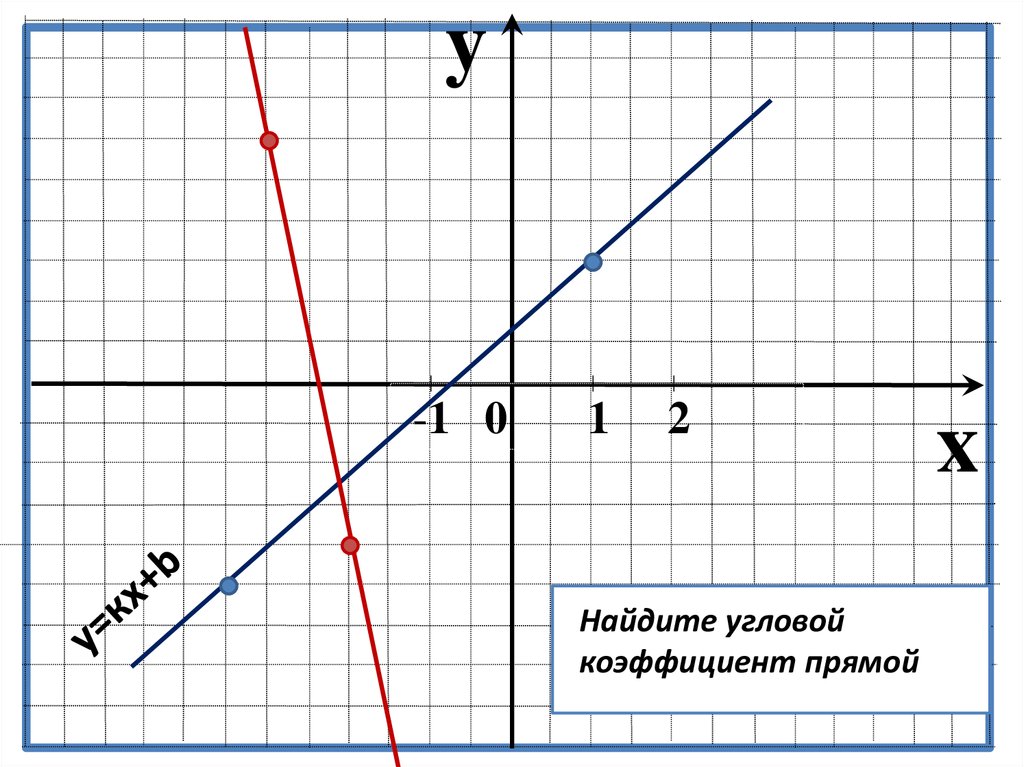
12.
y-1 0
1
2
Найдите угловой
коэффициент прямой
x
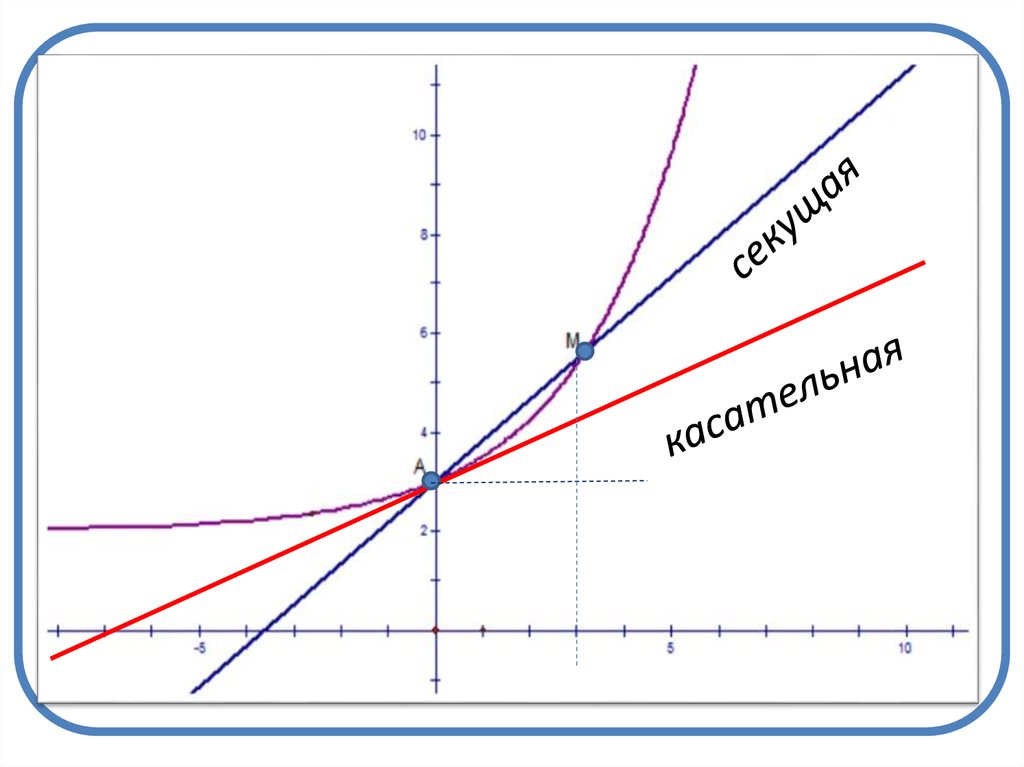
13. Определение
• Касательной к графику функцииу=f(x) называется предельное
положение секущей.
• рисунок
14.
15. Практическая исследовательская работа Геометрический смысл производной
Цель:Используя данные практической работы
определить, в чем состоит
геометрический смысл производной
Оборудование:
Линейки, транспортиры,
микрокалькуляторы, миллиметровая
бумага с построенным графиком
16. Задание
1. Постройте касательную к графику функции … в точкес абсциссой хₒ=2
2. Измерьте угол, образованный касательной и
положительным направлением оси оХ.
3. Записать =… .
4. Вычислите с помощью микрокалькулятора
tg =… .
5. Вычислите f´(xₒ ), для этого найдите f´(x)
6. Запишите: f´(x )=…. ; f´(xₒ )=….
7. Выберите две точки на графике касательной,
запишите их координаты.
8. Вычислите угловой коэффициент прямой k по
формуле k y1 y0
x1 x0
9. Результаты вычисления внесите в таблицу
17. Геометрический смысл производной
Значение производной функцииy=f(х) в точке х0 равно угловому
коэффициенту касательной к
графику функции y=f(х) в точке
(х0;f(x0))
k f ( x0 ) tg
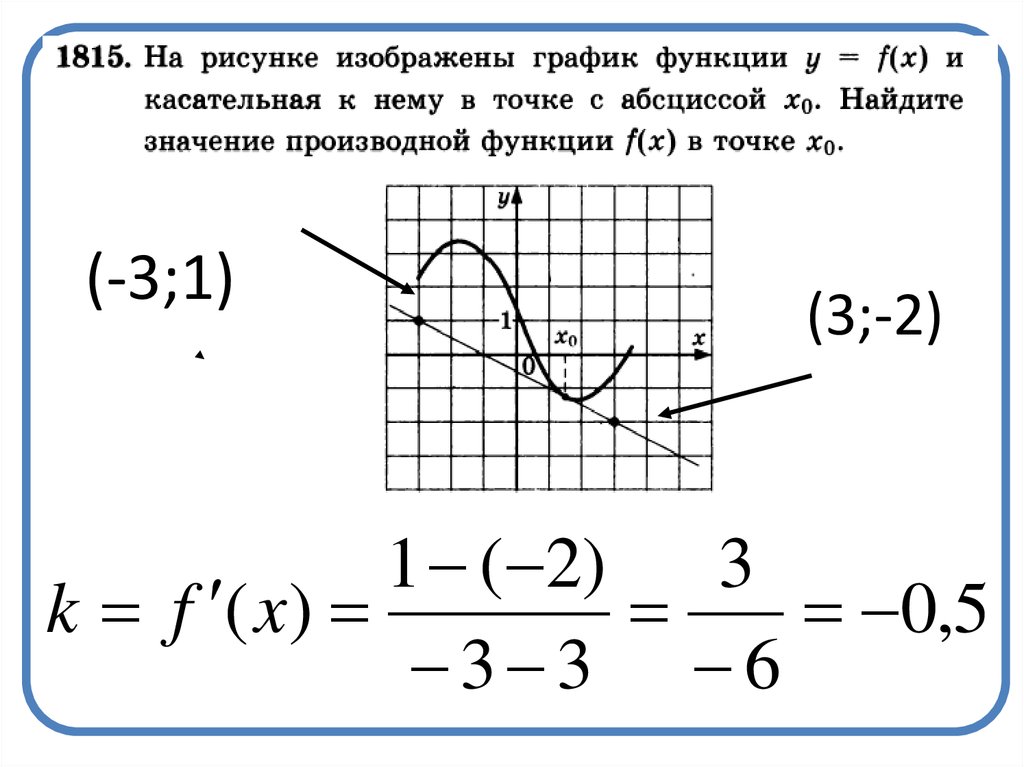
18.
(-3;1)(3;-2)
1 ( 2)
3
k f ( x)
0,5
3 3 6
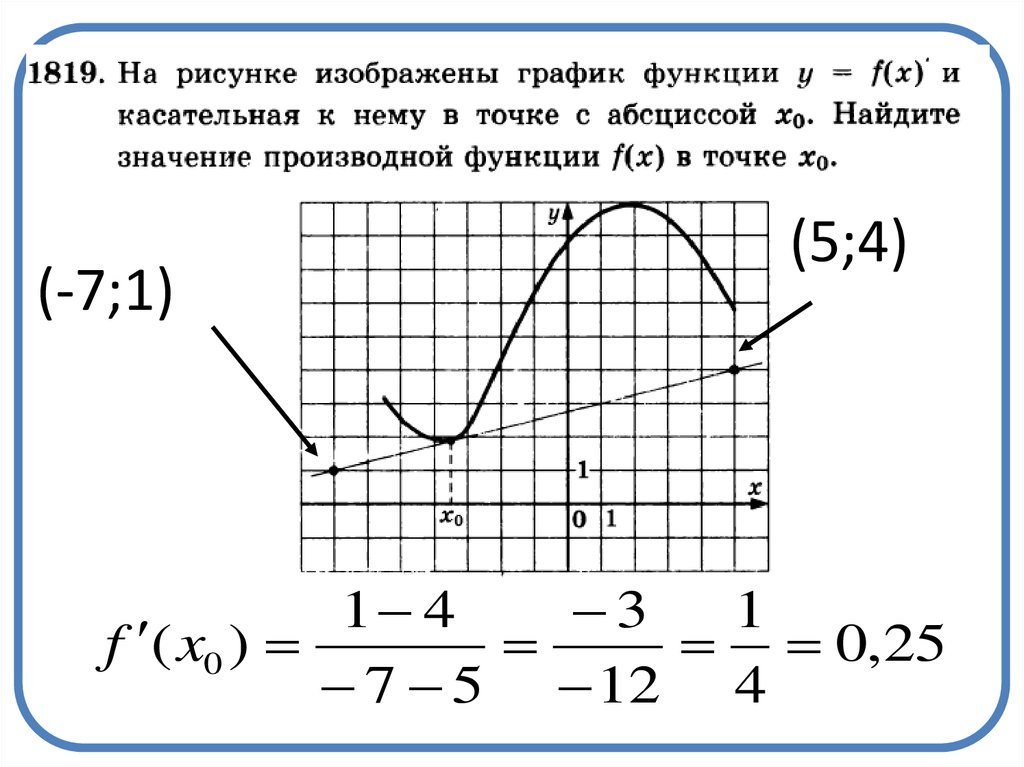
19.
(-7;1)(5;4)
1 4
3
1
f ( x0 )
0,25
7 5 12 4
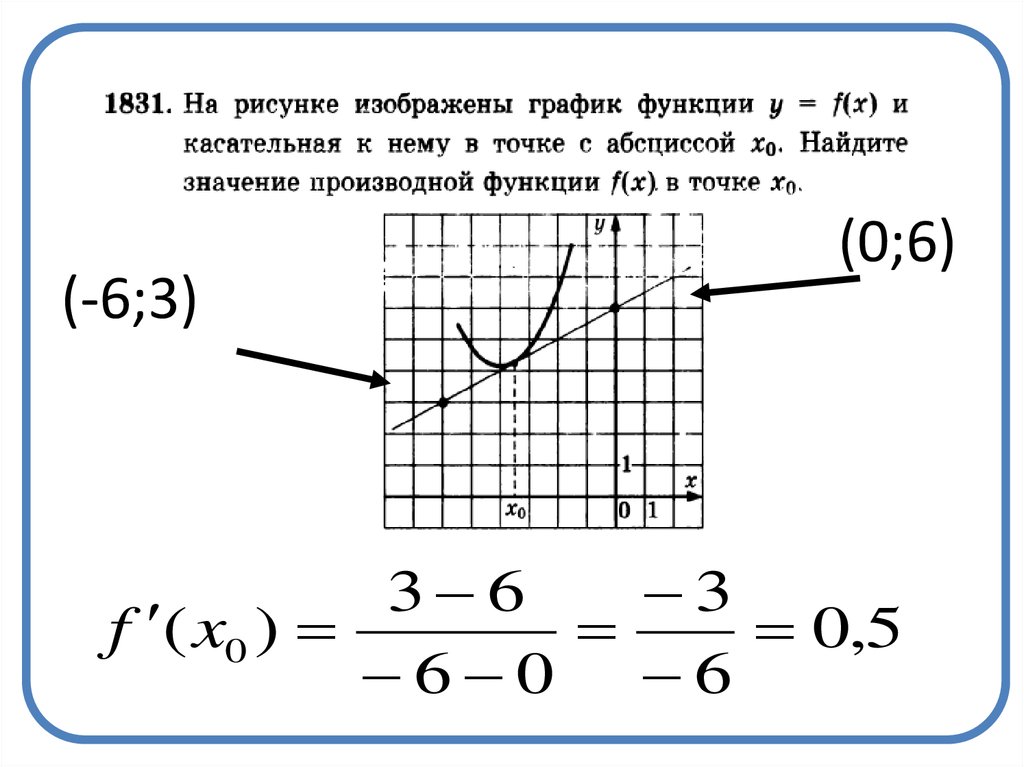
20.
(-6;3)(0;6)
3 6
3
f ( x0 )
0,5
6 0 6
21. Уравнение касательной к графику функции
1. Запишите уравнение прямой с угловымкоэффициентом k, проходящую через
точку ( х0 ; у0 )
у=у0+k(x-x0)
2. Замените k на f | ( xo ) , а у 0 на f ( x0 )
у f ( x0 ) f ( x0 )( x x0 )
|
22. Алгоритм составления уравнения касательной
1. Запишите уравнение касательной кграфику функции у f (x) в точке с
абсциссой х0 в общем виде.
2. Найдите производную функции у f (x) .
3. Вычислите значение производной
у0 f | ( x0 )
4. Вычислите значение функции в точке
у0 f ( x0 )
5. Подставьте найденные значения в
уравнение касательной
х0
23. Задача 1
Напишите уравнение касательной кграфику функции у=f(x) в точке с
абсциссой х0 .
3
2
f ( x) x x 1, x0 1.
1. y f ( x0 ) f | ( x0 )( x x0 );
2. f ( x) 3 x 2 x;
|
2
3. f | (1) 3 12 2 1 5;
4. f (1) 3;
5. y 3 5( x 1);
y 5 x 2.
24.
У меня всёполучилось
!!!
25.
26. Литература.
1. Алгебра и начала математического анализа11 класс Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М. И.
Шабунин.
2. ЕГЭ: 3000 задач с ответами по математике. Все задачи
группы В /А.Л.Семенов, И.В.Ященко, И.Р.Высоцкий и др./
3. http://prezentacii.com/matematike/116-prezentaciyageometricheskiy-smysl-proizvodnoy-v-zadaniyah-urovnyav.html (слайд 24,25)
4. Программа «Живая математика»















 mathematics
mathematics








