Решение показательных уравнений методом введения новой переменной

1.

Решение показательных
уравнений методом введения
новой переменной
Поречная Ирина Викторовна
МКОУ «Суджанская средняя
общеобразовательная школа
№2» Суджанского района
Курской области
учитель математики

2.

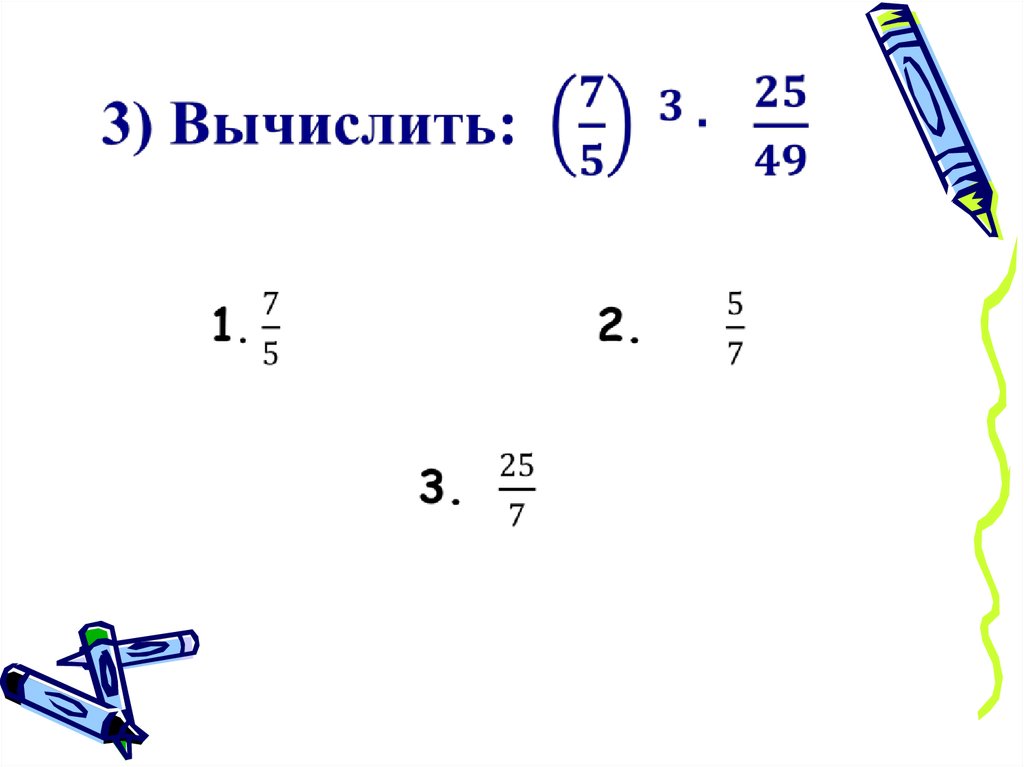
3. Тестовые задания

4.

5.

6.

4) Какое из уравнений не
имеет корней?
1. 3х+1=3
2. 6х=10
3. 3х =0

7.

5) Какое из уравнений
решено графически?

8.

9.

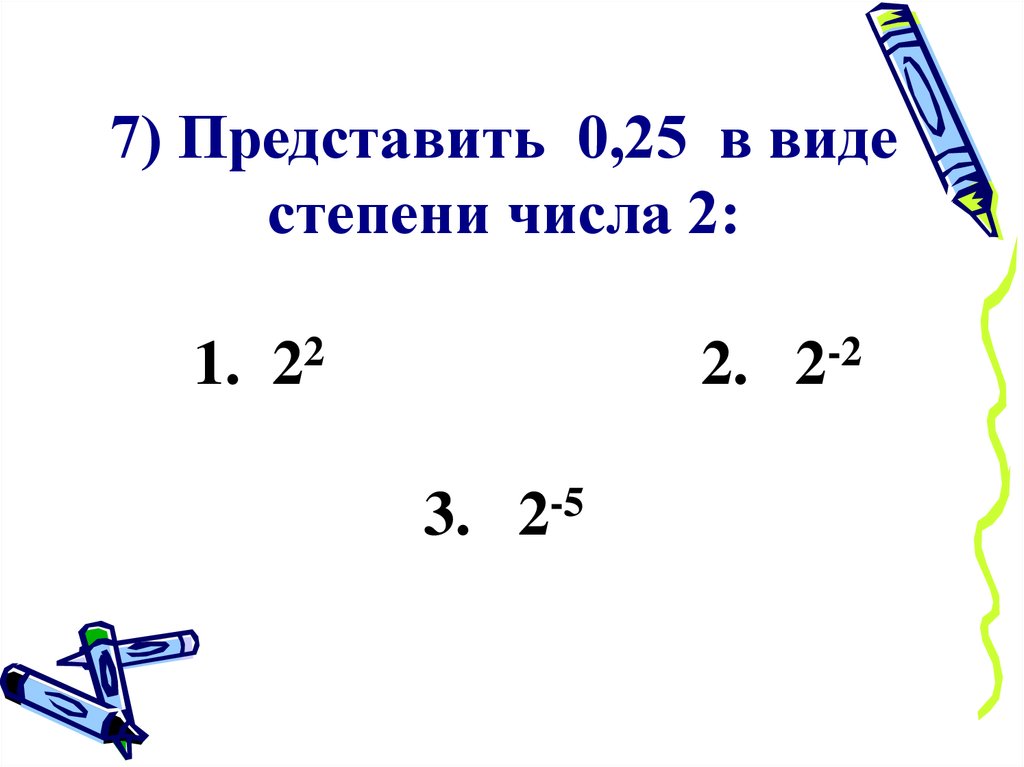
7) Представить 0,25 в виде
степени числа 2:
1. 22
2. 2-2
3.
-5
2

10.

Какие уравнения называются
показательными?

11. Тема урока: Решение показательных уравнений методом введения новой переменной

12.

9x - 4 · 3x – 45 = 0
т.к. 9x = (32)x = 32x = (3x)2,
Пусть 3x = t, где t > 0
t2 – 4t – 45 = 0
По Виета
t1 = -5
t2 = 9
3x = -5
3x = 9
решений нет
х=2
Ответ: 2

13.

2-x
2
-
x-1
2
=1

14.

15.

Метод замены переменной
применяют, если
основания степеней одинаковые
а) показатель одной степени в 2
раза больше, чем другой;
х
2x
Например: 3 – 4 · 3 – 45 = 0
б) коэффициенты при степенях
противоположны.
2-х
х–1
Например: 2
–2
=1

16.

17.

18.

19.

20.

21.

22.

23.

24. 1 группа - вынесением множителя за скобки 2 группа - заменой переменной 3 группа - делением на показательную функцию 4 группа -

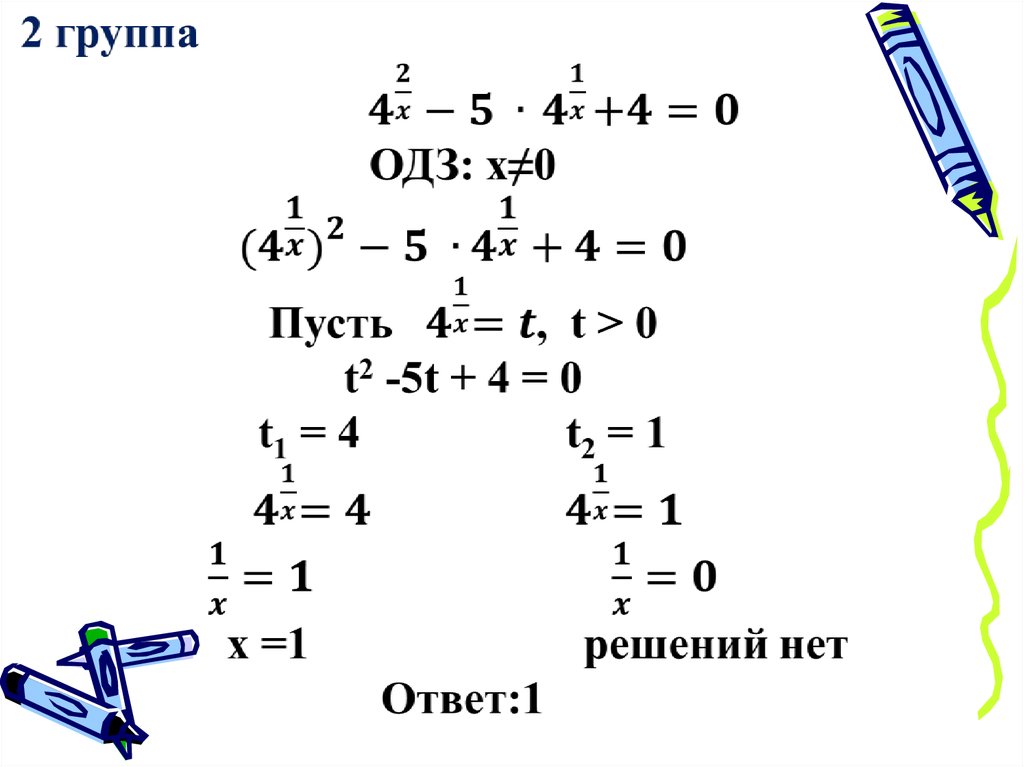
1 группа
2 группа
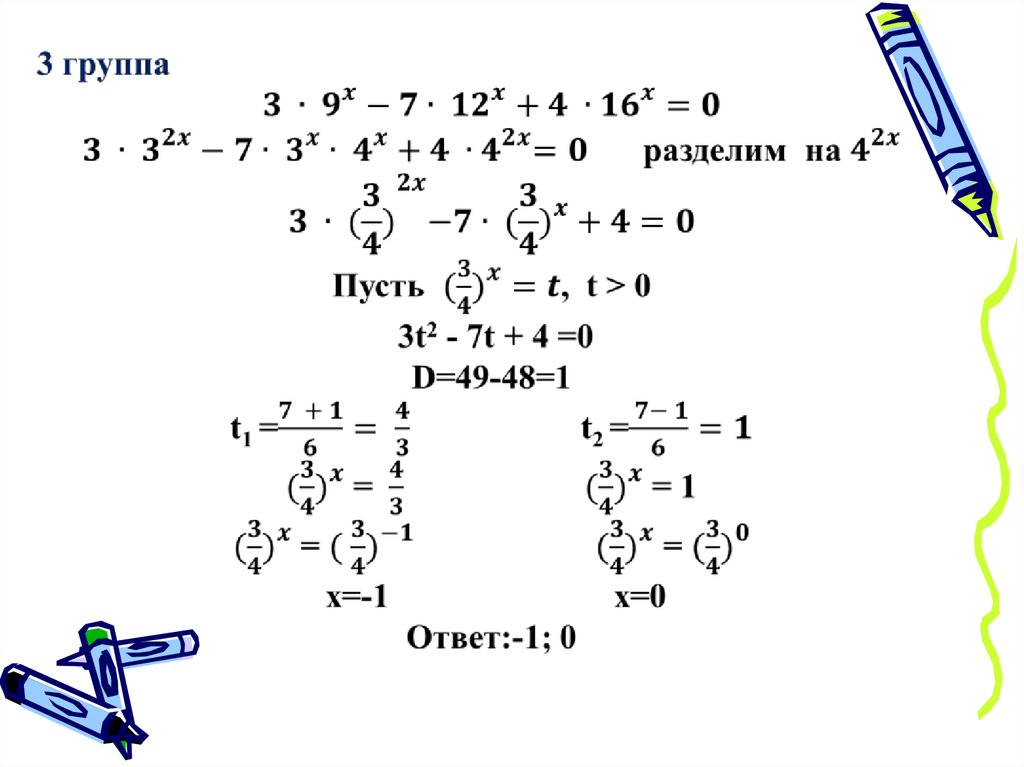
3 группа
4 группа
- вынесением множителя за скобки
- заменой переменной
- делением на показательную функцию
- уравнение, которые не имеет корней

25.

26.

Способ замены переменной
используют, если
1) основания степеней одинаковы,
но показатель ……… ……………
в 2 раза больше, чем другой;
2∙ 52x + …… + 4 = 0
2)основания степеней одинаковы,
но
коэффициенты
при
степенях ………...
4∙5х - …….. +3= 0

27.

Деление на показательную
функцию используется, если
основания степеней …………….
ax = bx
делим на ………

28.

Деление на показательную функцию
используется, в уравнениях вида
Aa2x+Baxbx+Cb2x =0.
Делим на ……., получим уравнение
вида…………………………., которое
решается с помощью замены
……….