Преобразование графиков функций

1.

Алгебра
9 класс
Автор: Егорова Раушания Леонидовна
учитель математики, высшей
квалификационной категории,
МБОУ «Гимназия №2 имени Мулланура
Вахитоваша», города Набережные Челны,
Республики Татарстан
2015г.

2. «График – это говорящая линия, которая может о многом рассказать» М.Б. Балк

Функция
– это
n
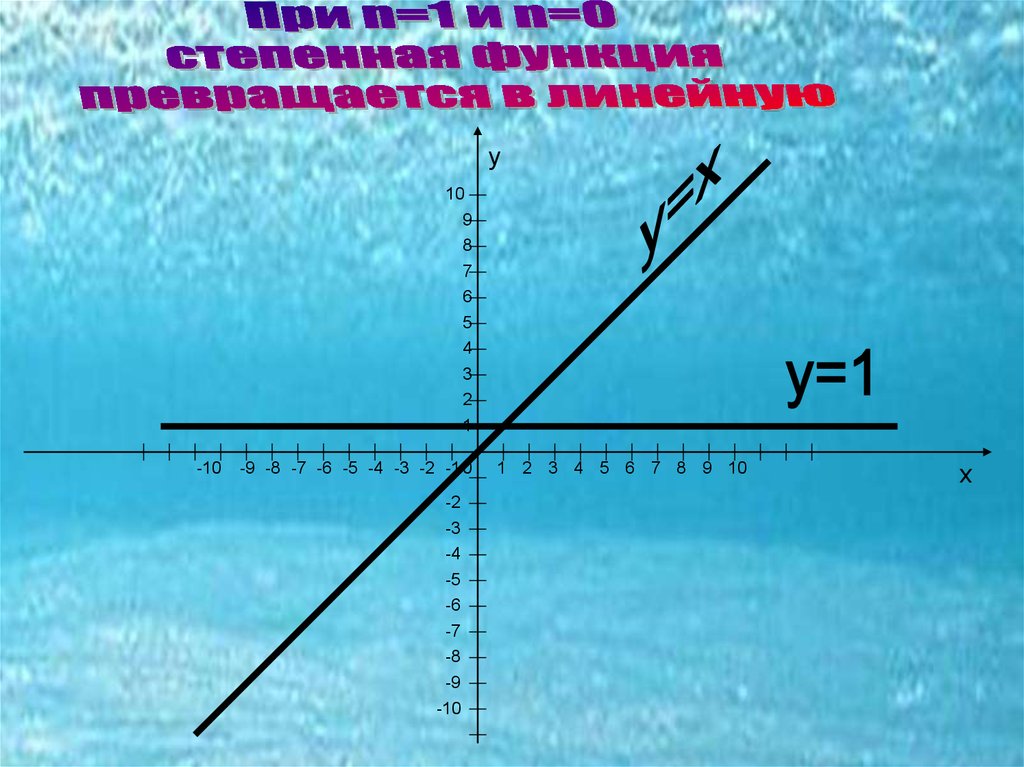
у=х
море, скрывающее в своей глубине
много тайн .
Приятного погружения!

3.

n
у=х
2
ï
3
n= -1
3
ï
4
n=2
4
ï
3
n=4
1
ï
3
n=0
1
ï
2
n=1
n=3
ï 2

4. Степенной функцией называется функция вида у=хn ,где х-независимая переменная, а n- любое действительное число, называемое

Гипербола – что это?

5.

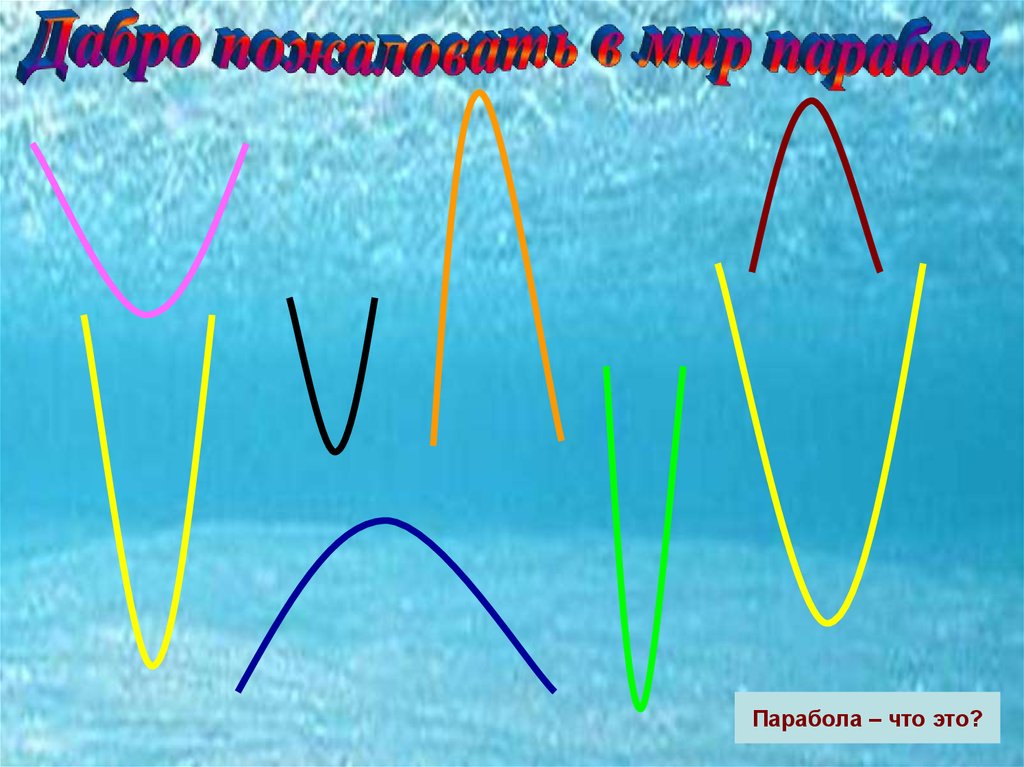
Парабола – что это?

6.

Слово «парабола» применяют часто ко всем кривым,
уравнение которых являются степенной функцией.
что это?

7. Слово «парабола» применяют часто ко всем кривым, уравнение которых являются степенной функцией.

что это?

8.

у
10
9
8
7
6
5
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

9.

Гипербола и парабола
– это кривые, получающиеся при сечении
кругового конуса (точнее – конической
поверхности) плоскостью, не проходящей
через его вершину.
Получающиеся при этом ограниченные
фигуры оказываются эллипсами, а
неограниченные – гиперболами (если секущая
плоскость пересекает обе полости конуса) или
параболами (если секущая плоскость
пересекается лишь с одной из его полостей).
Греческое слово «парабола»означает
«приложение»(так как в греческой геометрии
превращение прямоугольника данной площади у2 в
равновеликий ему прямоугольник с данным основанием
2р называлось приложением данного прямоугольника к
этому основанию); слово «эллипс» означает
«недостаток» (приложение с недостатком), слово
«гипербола» - «избыток» (приложение с избытком).

10. Гипербола и парабола – это кривые, получающиеся при сечении кругового конуса (точнее – конической поверхности) плоскостью, не

Все графики функции у=хn весьма
дисциплинированы, и действуют только по
законам.
Каждый график соблюдает свои права и
обязанности.
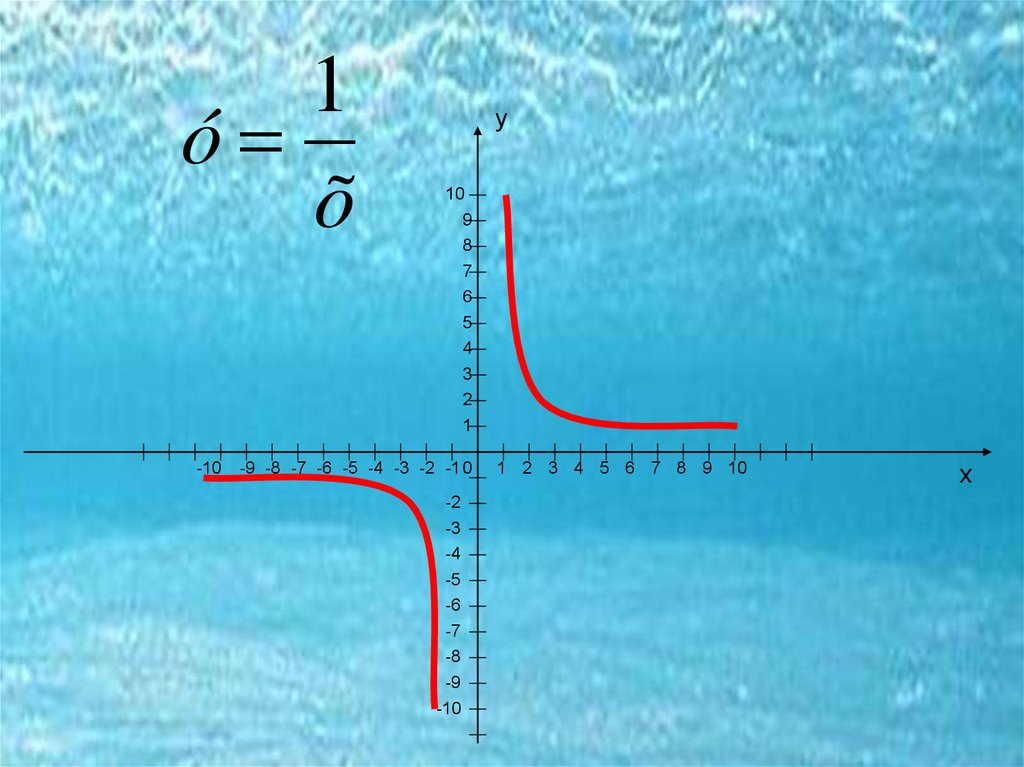
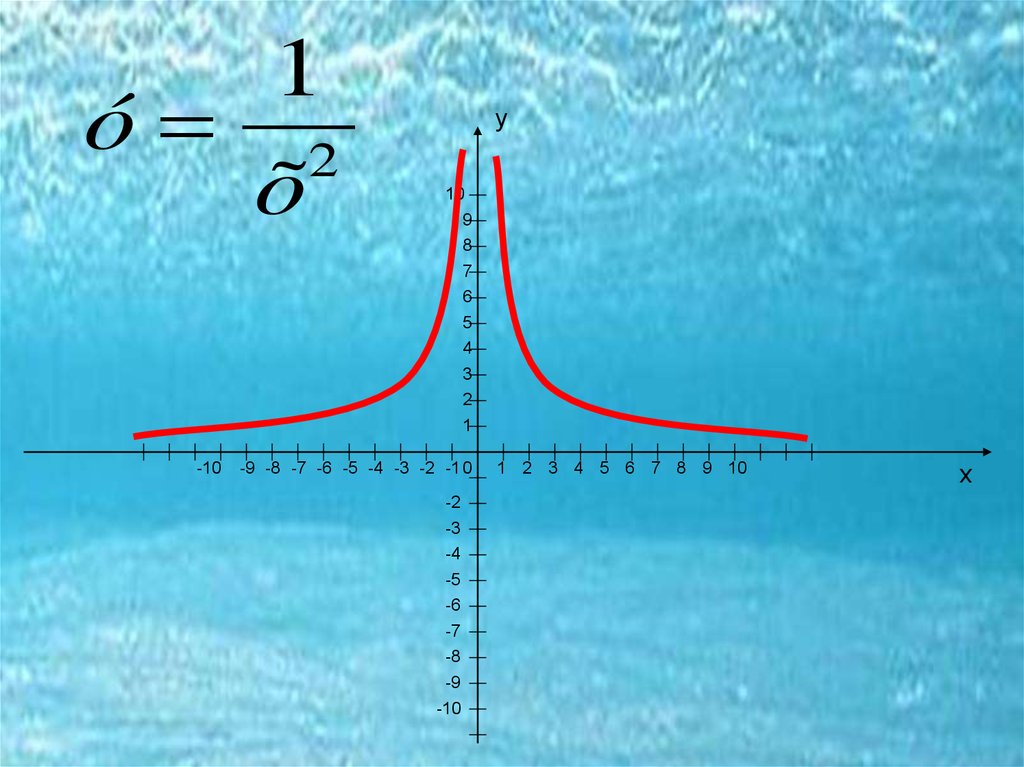
1) Если n – отрицательное целое число, то
степенная функция определяется равенством у=1/xn.
Она определена при всех отличных от нуля х. Её
график состоит из двух частей (ветвей), имеющих
асимптотами оси координат, к которым эти кривые
неограниченно приближаются.
Например

11. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

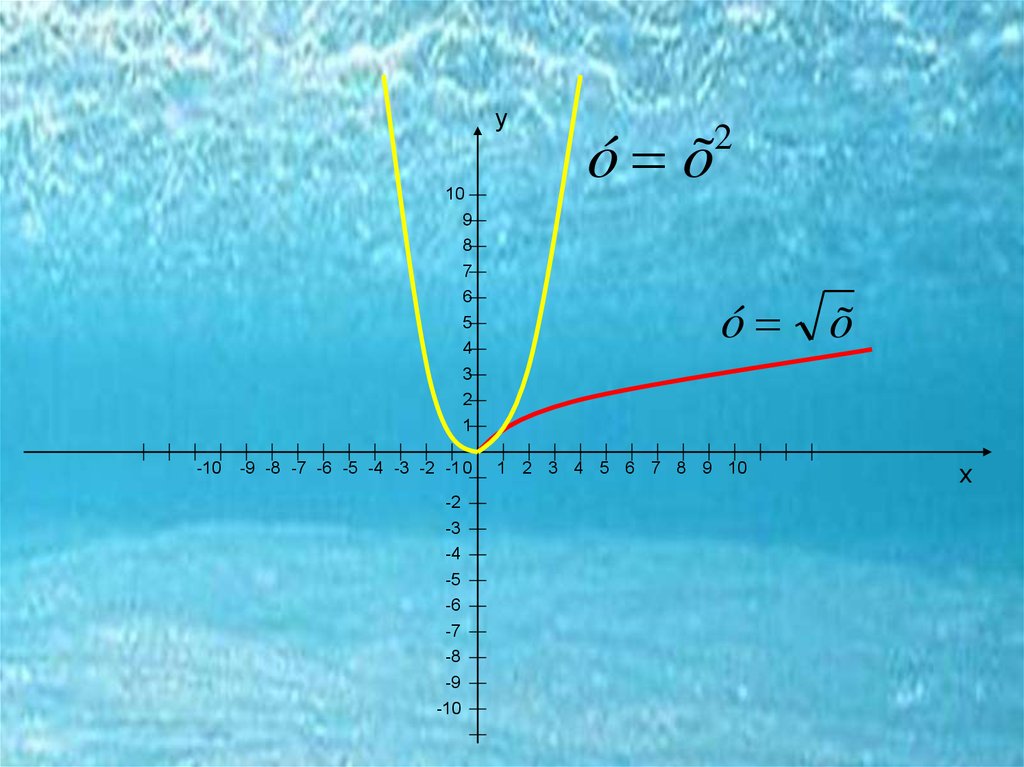
обязанности.
2) При n=1/α, где α – натуральное число, то
степенная функция определяется равенством у= õ
Она определяется, как обратная функция для
функции у=хα . При четном α функция определяется
лишь для х≥0, а при нечетном α – на всей оси
Например

12. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

13.

Все графики функции у=хn весьма
дисциплинированы, и действуют только по законам.
Каждый график соблюдает свои права и
обязанности.
3) При движении функции у=хn влево,
надо к аргументу х прибавить число в>0.
Например: у=(х+в)n
4) При движении функции у=хn вправо,
надо из аргумента х вычесть число в>0.
Например: у=(х-в)n

14. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

обязанности.
5) При движении функции у=хn вверх надо, к
значению функции прибавить число в>0.
Например: у=хn+в
6) При движении функции у=хn вниз надо, к
значению функции прибавить число в<0.
Например: у=хn+в

15. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

обязанности.
5) При необходимости перевернуть функцию
у=хn надо значение функции умножить на -1.
Например: у=-хn
6) При необходимости растянуть функцию
у=хn надо значение функции умножить на число к>1.
Например: у=кхn
7) При необходимости сжать функцию у=хn
надо значение функции разделить на число к>1.
Например: у=хn /к

16. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

обязанности.
8) При необходимости отобразить часть функции у=хn
лежащую в одной полуплоскости, относительно оси ОХ в
другую полуплоскость надо поставить знак модуля на
значение функции.
Например: у=IхnI
9) При необходимости отобразить часть функции у=хn
лежащую в одной полуплоскости, относительно оси ОY в
другую полуплоскость надо поставить знак модуля на
аргумент.
Например: у=IхIn

17. Все графики функции у=хn весьма дисциплинированы, и действуют только по законам. Каждый график соблюдает свои права и

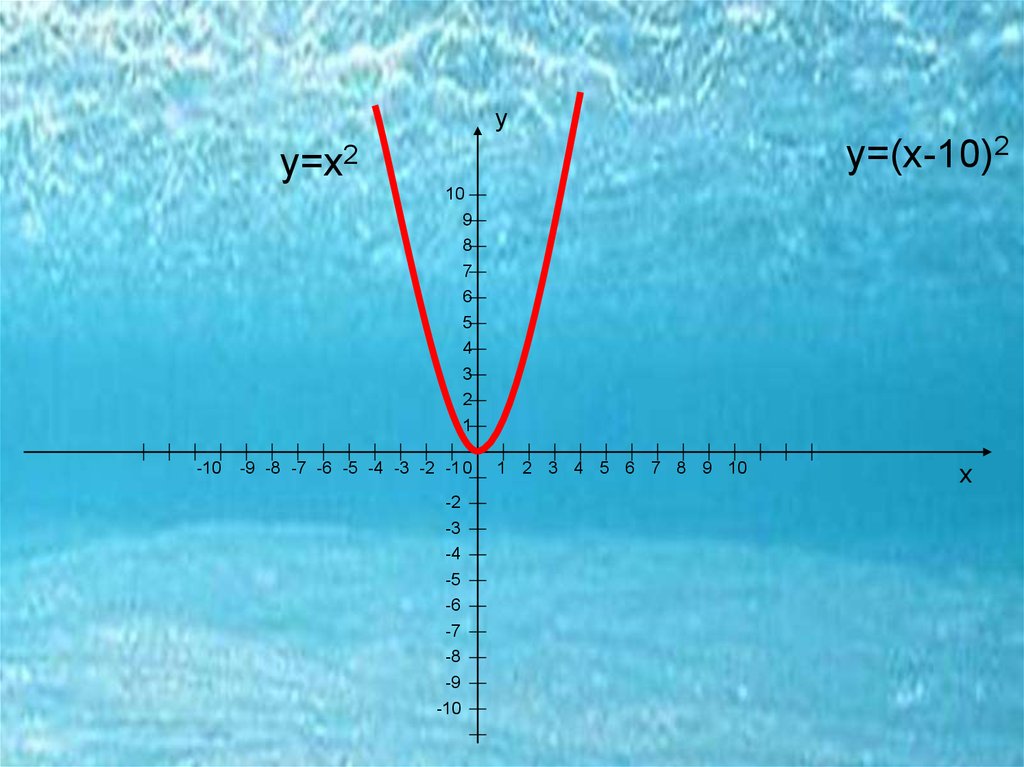
у
у=х2
у=(х-10)2
10
9
8
7
6
5
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

18. у=(х-10)2

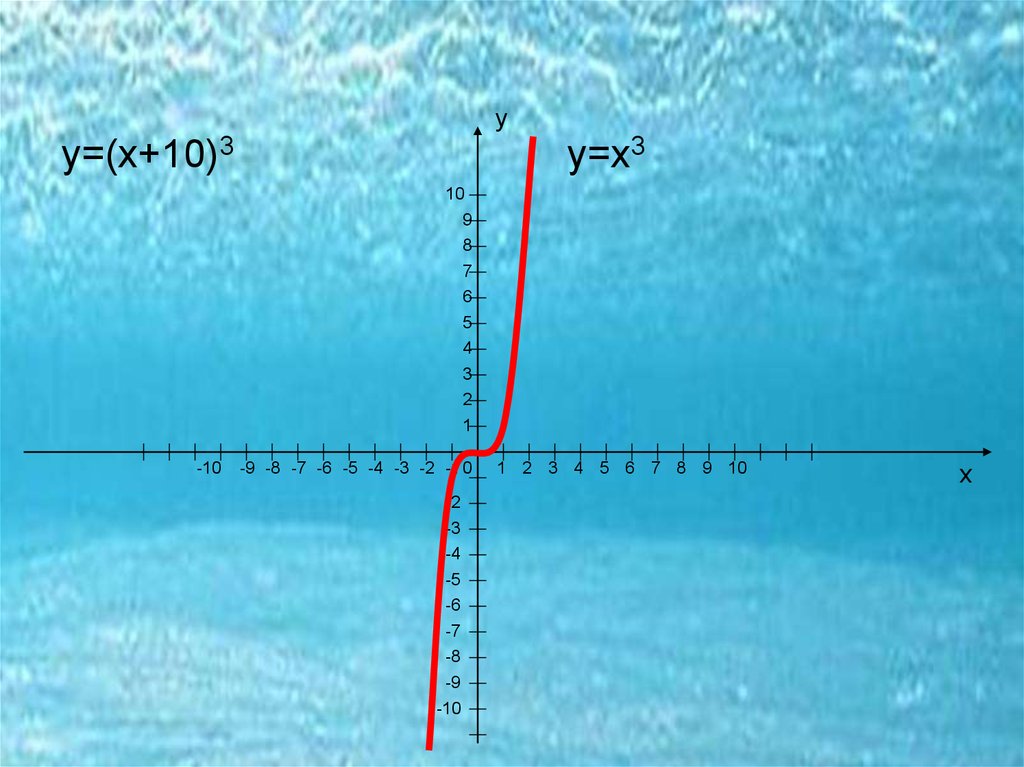
у
у=(х+10)3
у=х3
10
9
8
7
6
5
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

19. у=х3

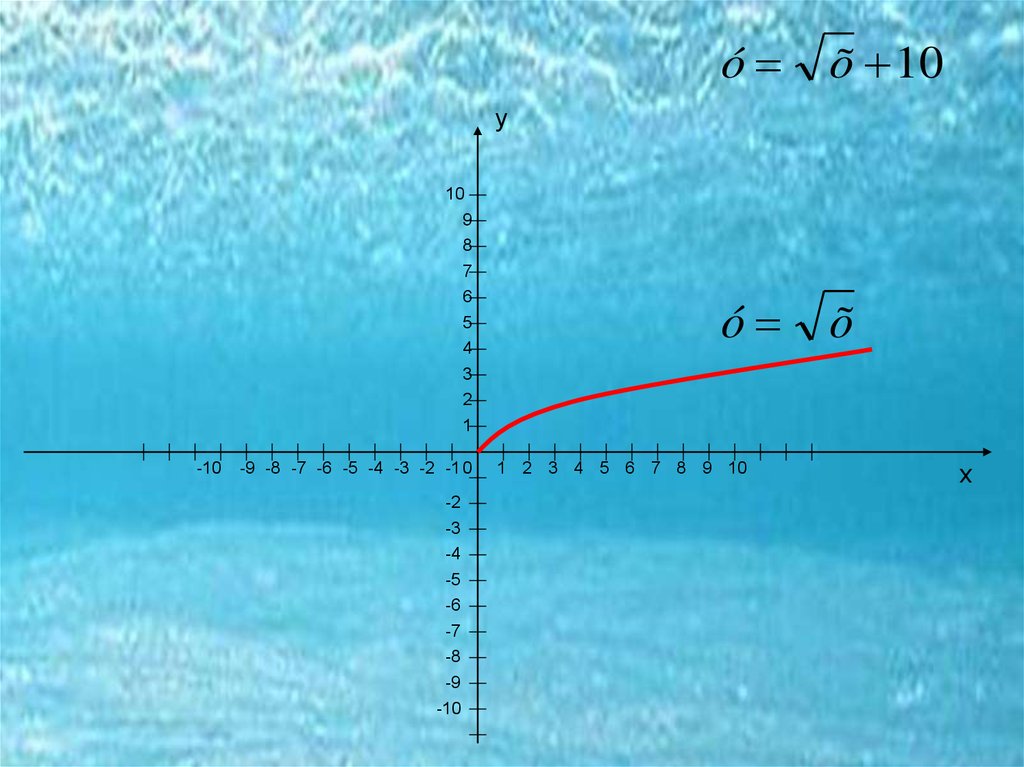
ó
õ 10
у
10
9
8
7
6
5
4
ó õ
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

20.

у
10
9
8
7
6
5
4
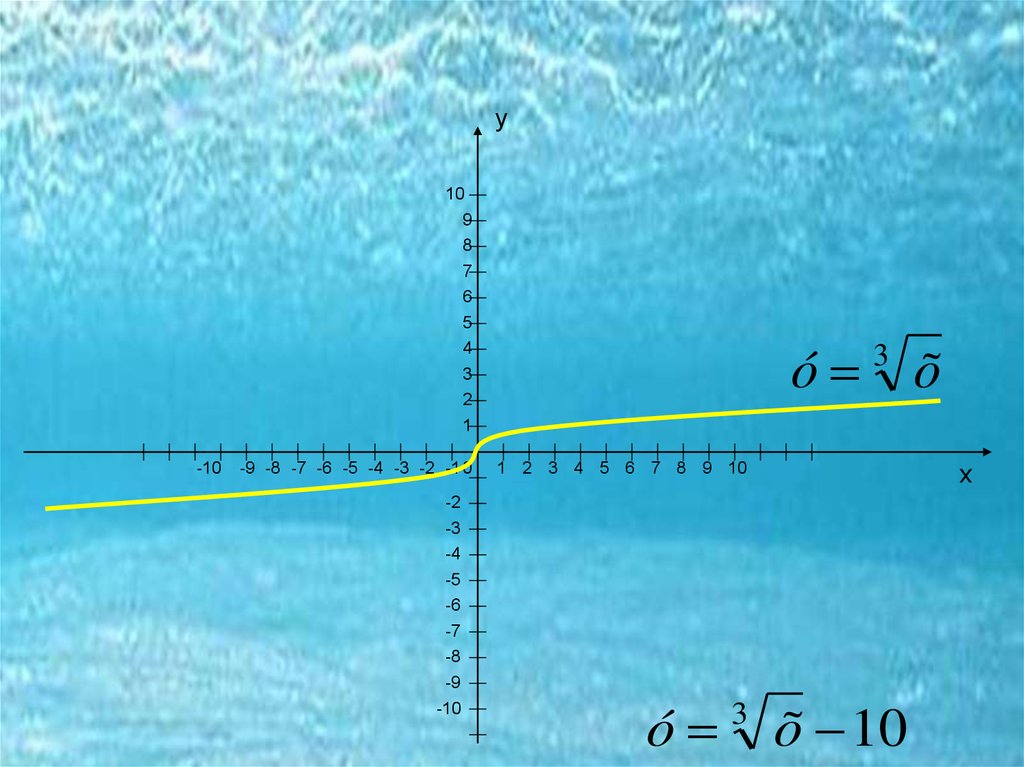
ó õ
3
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
1 2 3 4 5 6 7 8 9 10
-2
-3
-4
-5
-6
-7
-8
-9
-10
ó 3 õ 10
х

21.

у
10
9
8
7
6
5
4
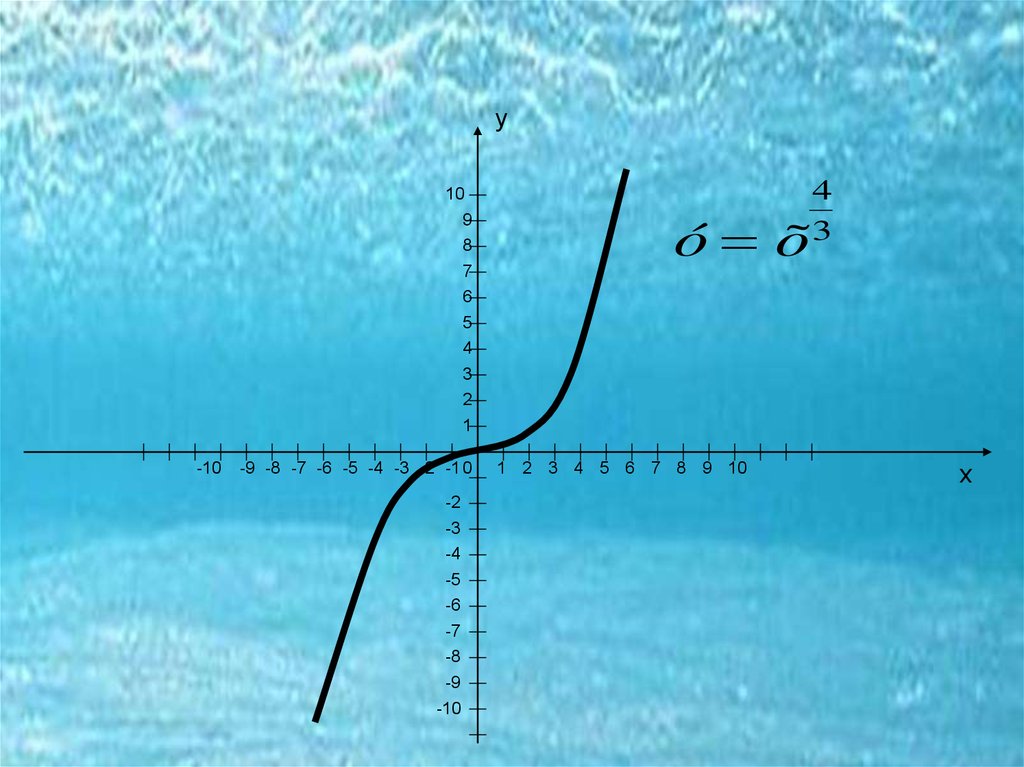
ó õ
4
3
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

22.

23.

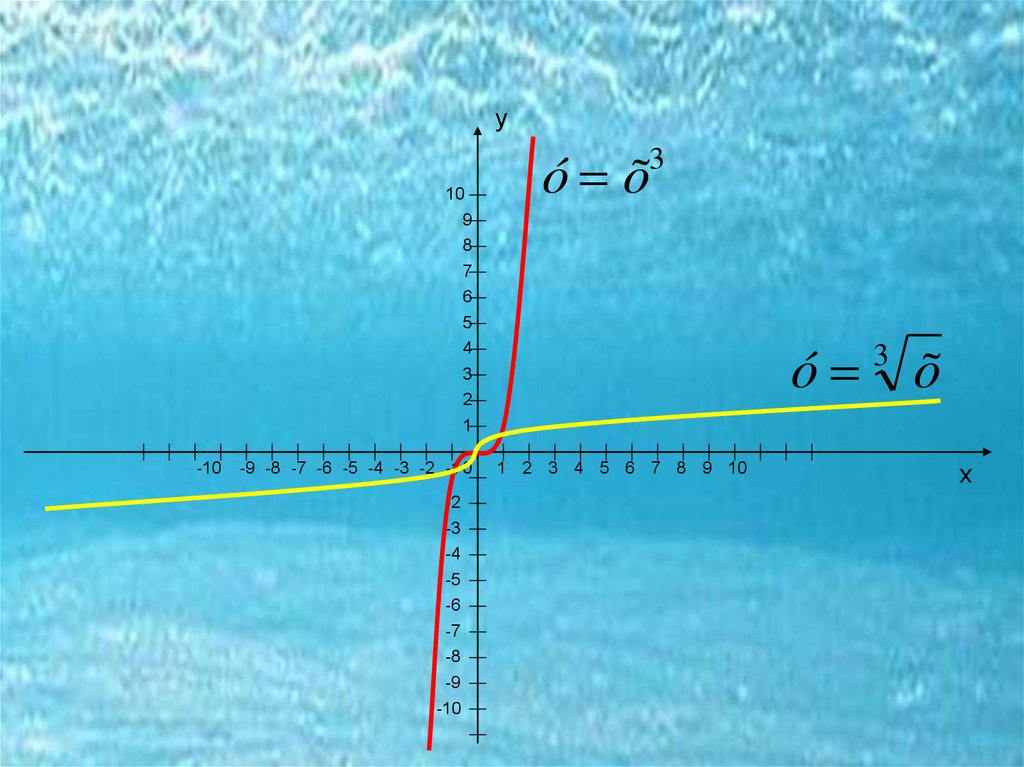
у
ó õ
3
10
9
8
7
6
5
4
ó õ
3
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

24.

у
10
9
8
7
6
5
4
ó õ
2
ó õ
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

25.

1
ó
õ
у
10
9
8
7
6
5
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

26.

1
ó 2
õ
у
10
9
8
7
6
5
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

27.

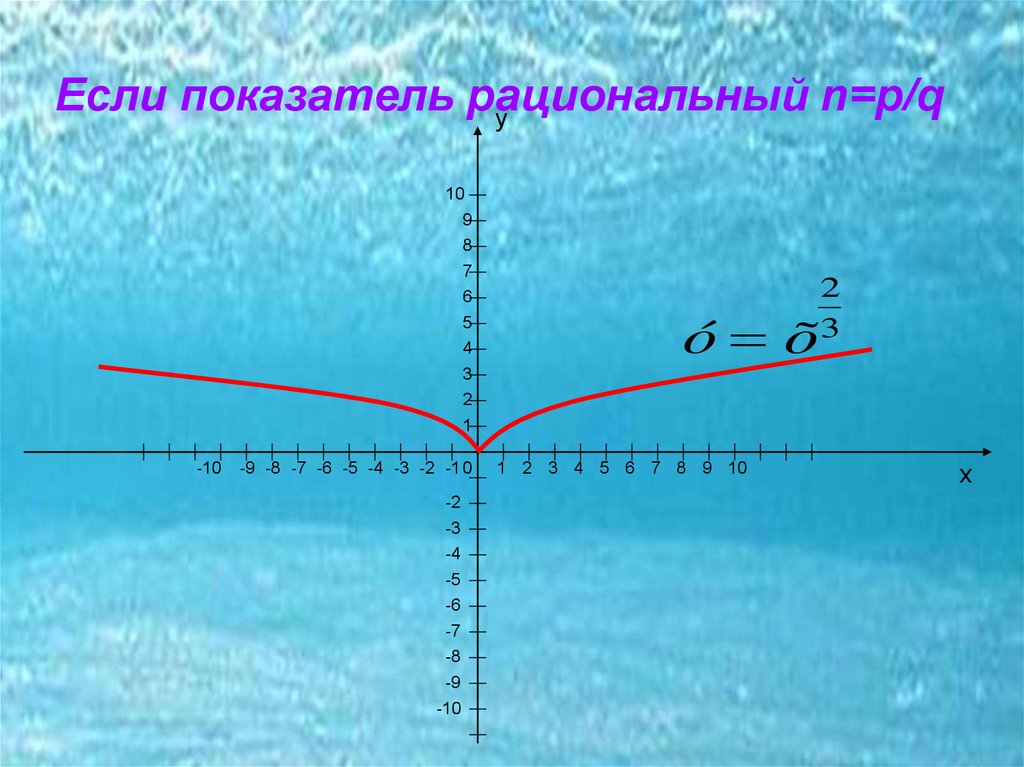
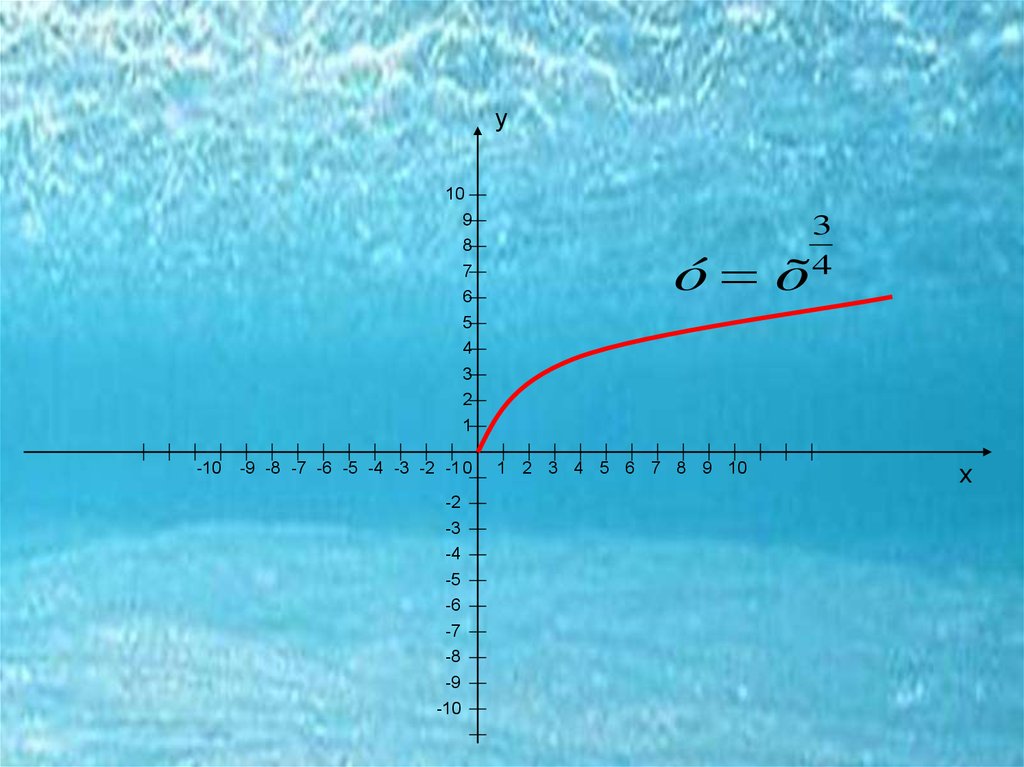
Если показатель рациональный
n=р/q
у
10
9
8
7
6
5
4
ó õ
2
3
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

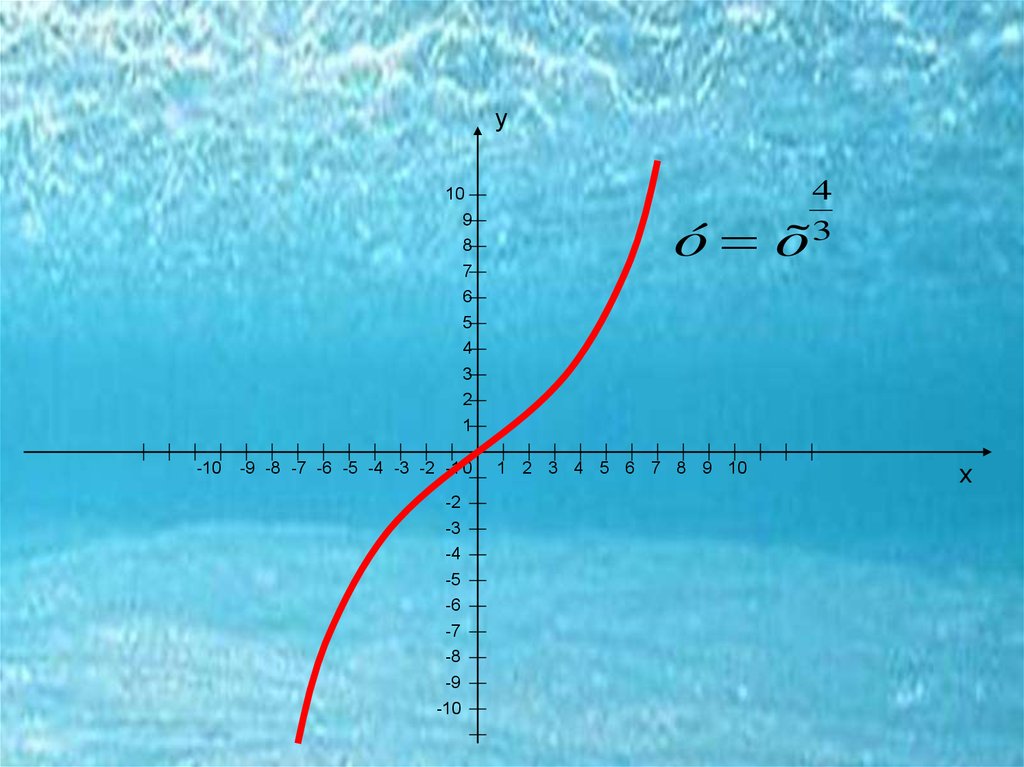
28. Если показатель рациональный n=р/q

у
10
9
8
7
6
5
4
ó õ
3
4
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х

29.

у
10
9
8
7
6
5
4
ó õ
4
3
3
2
1
-10
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
-10
1 2 3 4 5 6 7 8 9 10
х