Similar presentations:
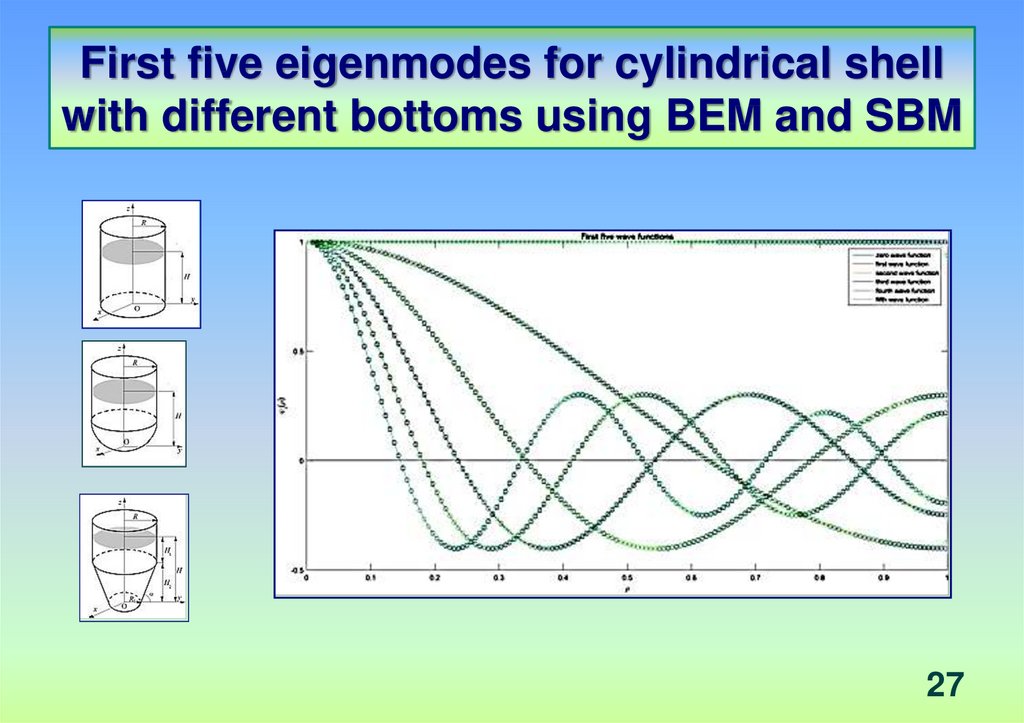
Singular boundary method in free vibration analysis of compound liquid-filled shells
1. 42nd International Conference on Boundary Elements and other Mesh Reduction Methods
SINGULAR BOUNDARY METHODIN FREE VIBRATION ANALYSIS
OF COMPOUND LIQUID-FILLED SHELLS
VASYL GNITKO, KYRYL DEGTYARIOV,
ARTEM KARAIEV,
ELENA STRELNIKOVA
V. N. Karazin Kharkiv National University
A. Podgorny Institute of Mechanical Engineering Problems
UKRAINE
1
2. A.N. Podgorny Institute of Mechanical Engineering Problems, National Academy of Sciences, Ukraine
23. CONTENTS
• Introduction and problem statement• Mode superposition method for coupled dynamic
problems
• Systems of the boundary integral equations and
some remarks about their numerical implementation
• Some numerical results
• Conclusion
3
4. A. Podgorny Institute of Mechanical Engineering Problems
• The A.N.Podgorny Institute for Mechanical Engineering Problemsof the National Academy of Sciences of Ukraine
• (IPMash NAS of Ukraine) is a renown research centre in
power and mechanical engineering.
IPMash has 5 research departments with a staff of 346 specialists (133
research workers, including one Academician and five Corresponding
Members of NAS of Ukraine; and 32 Doctors and 77 Candidates of
Science). The Institute also has a special Design-and-Engineering Bureau,
and a pilot production facility.
• Key research areas
optimisation of processes in power machinery
energy saving technologies
predicting the reliability, dynamic strength and life of power equipment;
simulation and computer technologies in power machine building
4
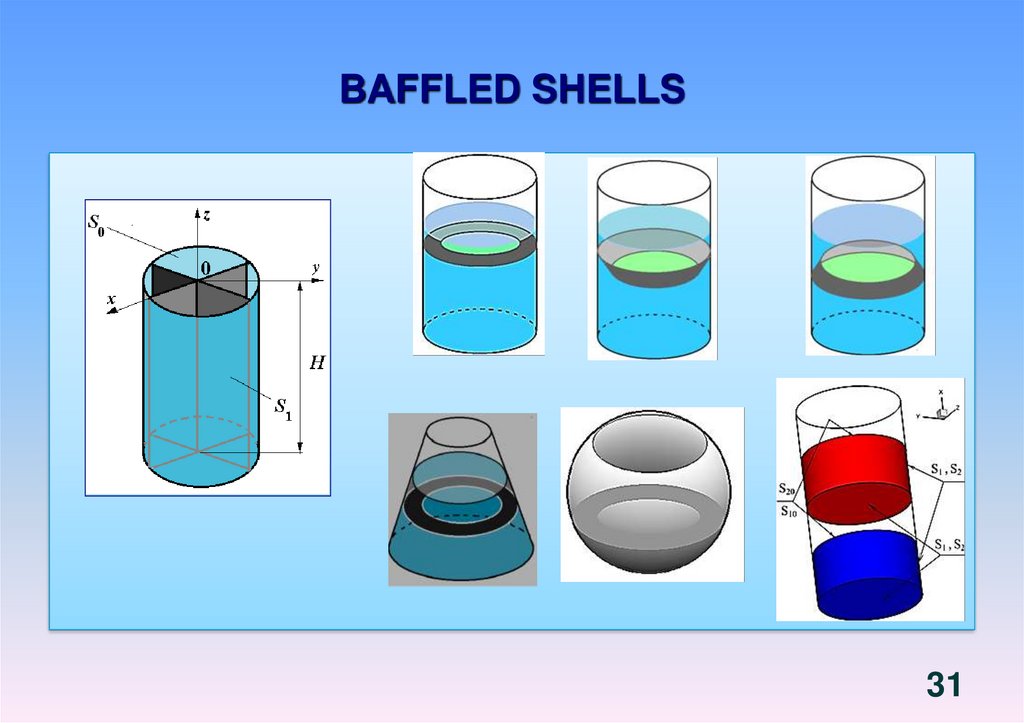
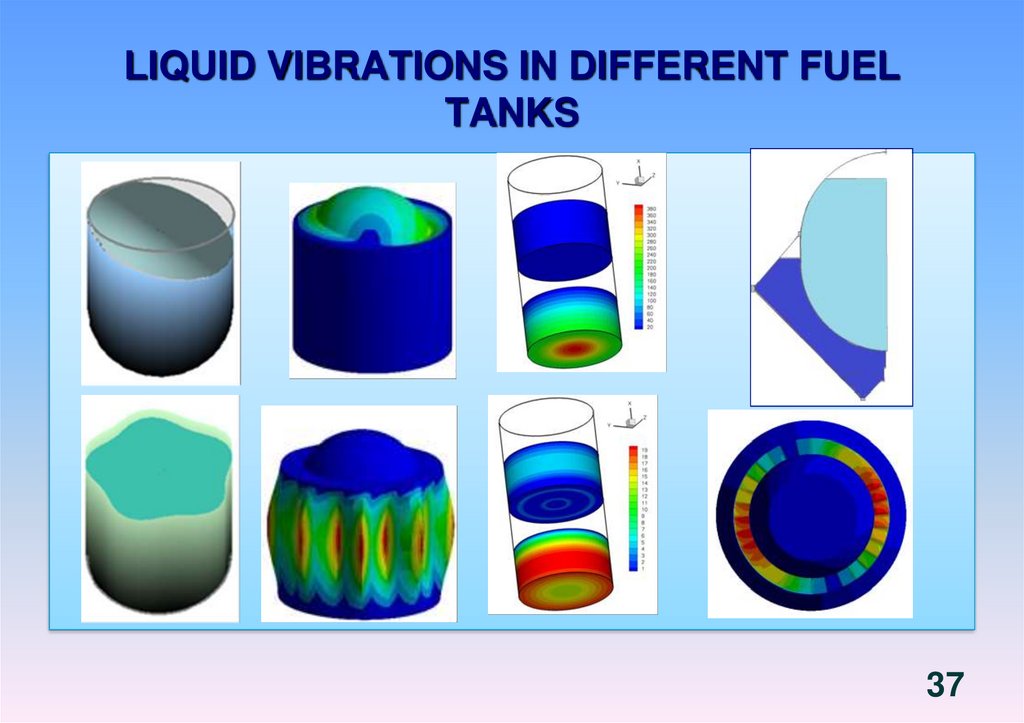
5. LIQUID FILLED SHELLS
56. PROBLEM STATEMENT
) pnL(U) M(U
0
p l
gz p0
t
• with the next set of boundary conditions relative to
w
n S1 t
n
S0
;
t
gz 0
t
s0
• w=(U,n)
• fixation conditions of the shell relative to U
• Initial conditions
x, y,0 H ; x, y,0 0
6
7. BOUNDARY CONDITIONS ON ELASTIC AND RIGID SURFACES
U , ngrad n s
; grad n s2 0
t
1
HARMONIC VIBRATIONS
7
8. MODE DECOMPOSITION METHOD FOR COUPLED DYNAMIC PROBLEMS
• Displacements are linear combination ofstructure natural modes without liquid
u
N
c u
k
k
k 1
uk are the normal modes of vibrations of the empty shell.
the first system of basic functions
Representation for velocity potential
1 2
8
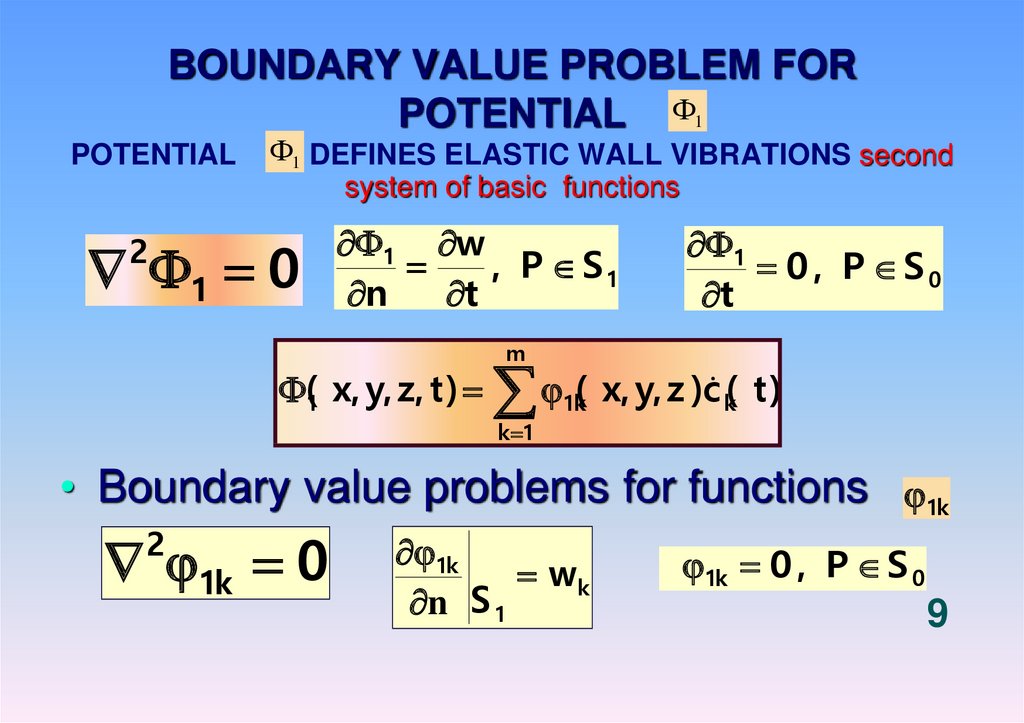
9. BOUNDARY VALUE PROBLEM FOR POTENTIAL
1POTENTIAL
1 DEFINES ELASTIC WALL VIBRATIONS second
system of basic functions
2
1 0
1 w
, P S1
n
t
(1 x, y, z, t )
1
0 , P S0
t
m
( x, y, z )c ( t )
1k
k
k 1
• Boundary value problems for functions 1k
2
1k 0
1k
wk
n S 1
1k 0 , P S 0
9
10. Boundary value problem for velocity potential third system of basic functions
Boundary value problem for velocitypotential 2
third system of basic functions
2 2 0
2
2
0 , P S1
, P S0
n
n
2
g a s t x 0
t
s0
• representation for velocity potential
2
• harmonic vibrations of liquid in rigid shell
2( x, y, z, t ) ei t ( x, y, z )
2
• 0
0 , P S1
n
2
, P S0
n g
10
11. SPRING- PENDULUM ANALOGY
(1 x, y, z, t )m
( x, y, z )c ( t )
1k
k
k 1
11
12. Three systems of basic functions
• At first we obtain the natural modes and frequencies ofstructure without liquid – the first system of basic functions
• Second, we represent the velocity potential
• as a sum 1 2 and for each component consider the
corresponding boundary value problem for Laplace equation.
• The potential 1 corresponds to the problem of elastic
structure vibrations with the liquid but without including the
force of gravity - the second system of basic functions
• The potential 2 corresponds to the problem of rigid structure
vibrations with the liquid including the force of gravity • the third system of basic functions
12
13. EIGENVALUE PROBLEM
FOR HARMONIC VIBRATIONS WE HAVE
ck t Ck exp(i t );
d k t Dk exp(i t );
aS t 0
We use the direct BEM formulation
1
1
2 P0
dS
dS
n P P0
n P P0
S
S
13
14. FIRST AND SECOND BASIC FUNCTIONS
1415. VIBRATIONS OF RECTANGULAR PLATES
h, м0,00215
0,003
0,005
air.
experiment/
calculation
Reduction
coefficient
194/197
290/280
413/458
1,57
1,27
1,23
1
Liquid
Reduction
coefficient
Liquid
experiment
BEM
112
182
360
1
1,75
1,53
1,27
106
179
305
Reduction
coefficient
1,82
1,62
1,21
MODES OF VIBRATIONS
15
16. VIBRATIONS OF SECTORIAL PLATES
Number offrequencies, Hz
frequency
liquid
air
1
2
3
4
experiment
calculation
experiment
calculation
402
416
514
714
398.2
425.0
549.7
791.0
159
277
420
161
242
300
460
MODES OF VIBRATIONS
16
17. VIBRATIOBS OF FRANSIS TURBINE
Without added liquid massesNumber of
frequency
1
2,3
4,5
6,7
8
FEM
Leningrad metal plant
Experiment
TURBOATOM
experiment
33.05
35.80
42.90
71.90
80.70
33.68
37.13
39.87
57.89
80.44
33.87
35.93
63.06
66.99
83.83
With added liquid masses
Number of
frequency
1
2,3
4,5
6,7
8
FEM
24.00
29.20
31.50
37.00
52.50
Leningrad metal
plant
Experiment
22.5
28.5
31.1
33.3
TURBOATOM
experiment
21.6
28.5
32.7
37.2
40.2
17
18. FRANSIS TURBINE MODES OF VIBRATIONS
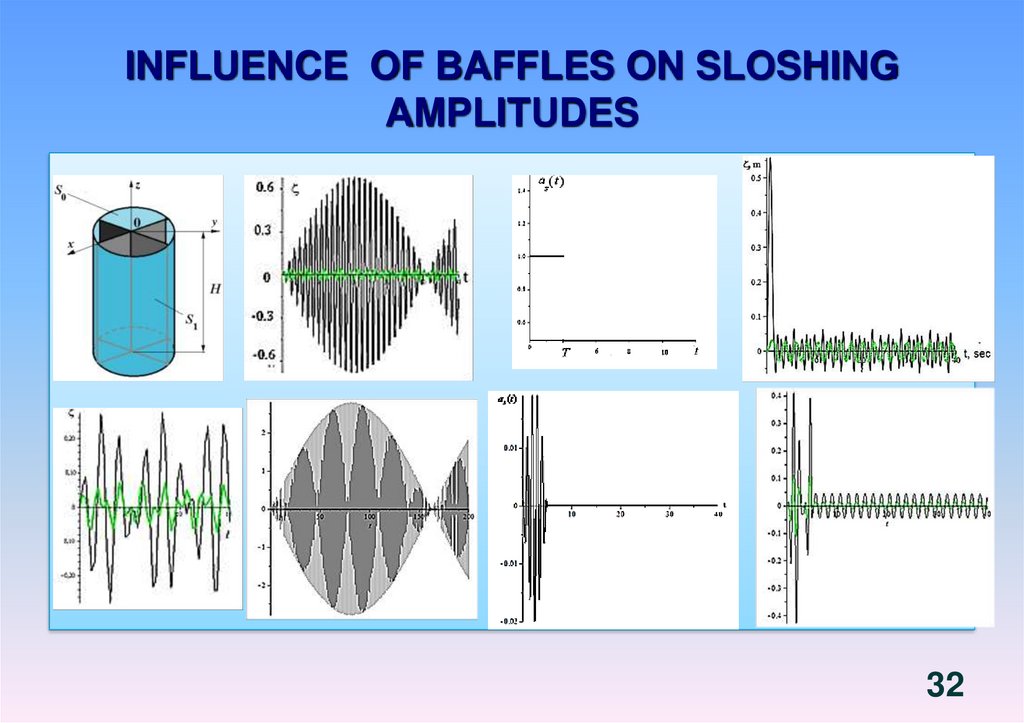
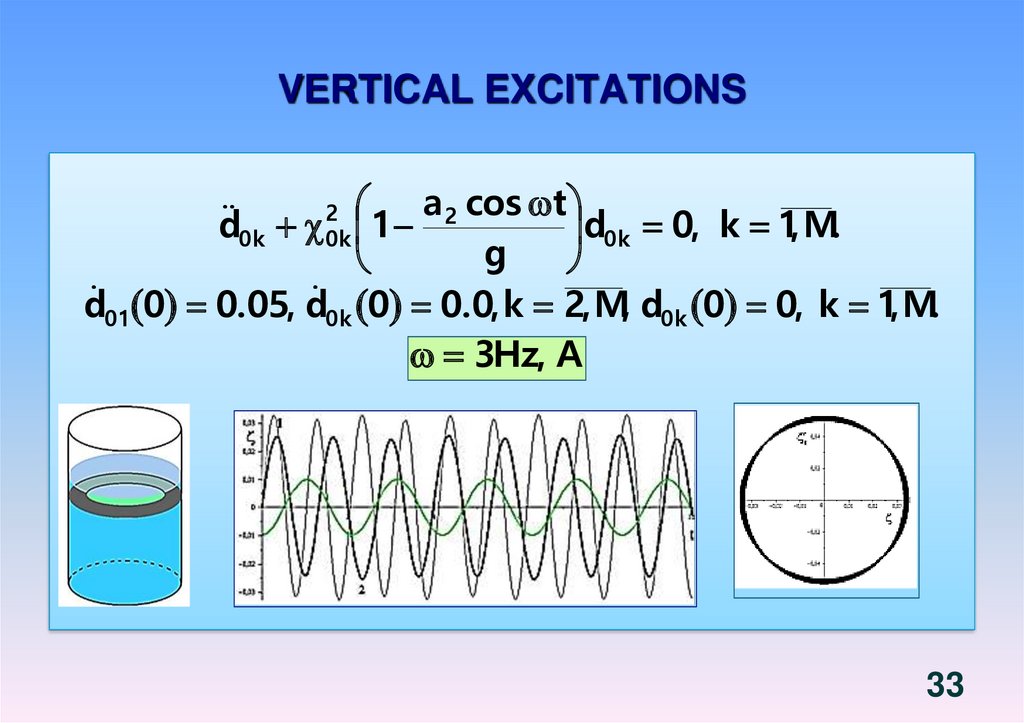
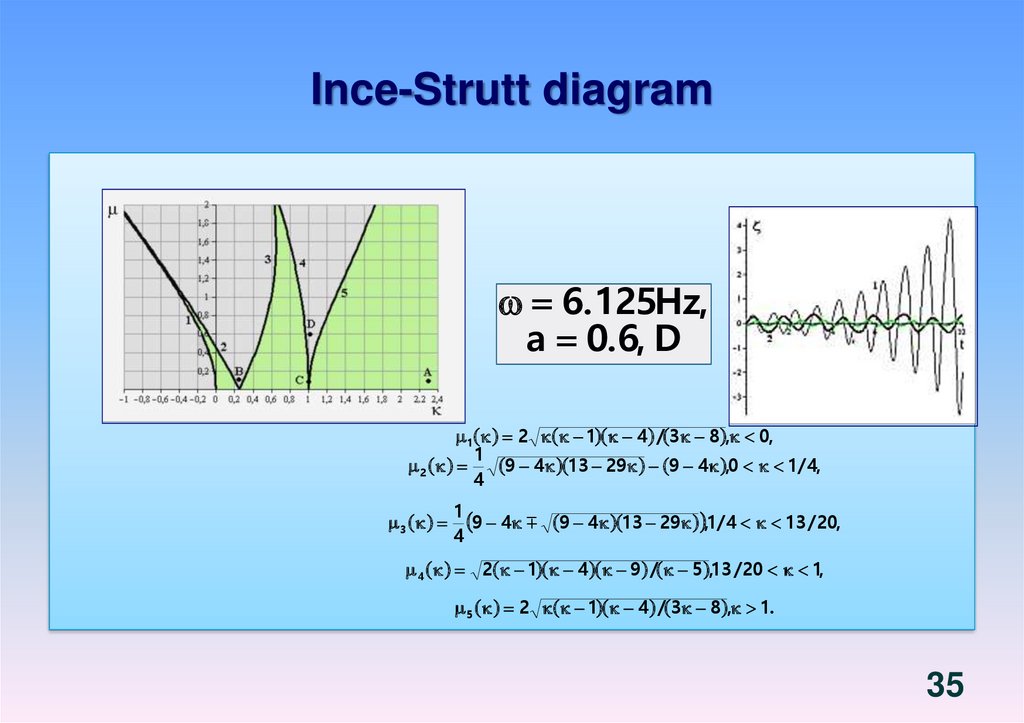
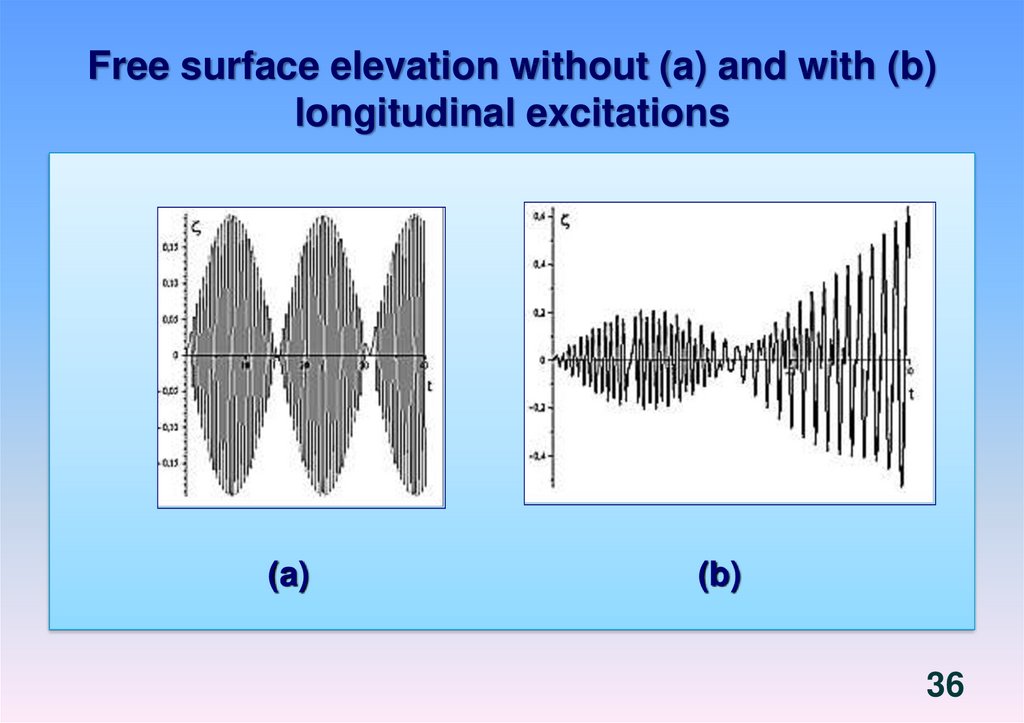
1819. Free vibrations of liquid in rigid shells. Boundary value problem. Third system of basic functions.
2 0( x, y, z, t ) ei t ( x, y, z )
0 , P S1
n
0
, P S0
z
0 , P S1
n
g 0 , P S0
2
Free vibrations
2
, P S0
n
g
19
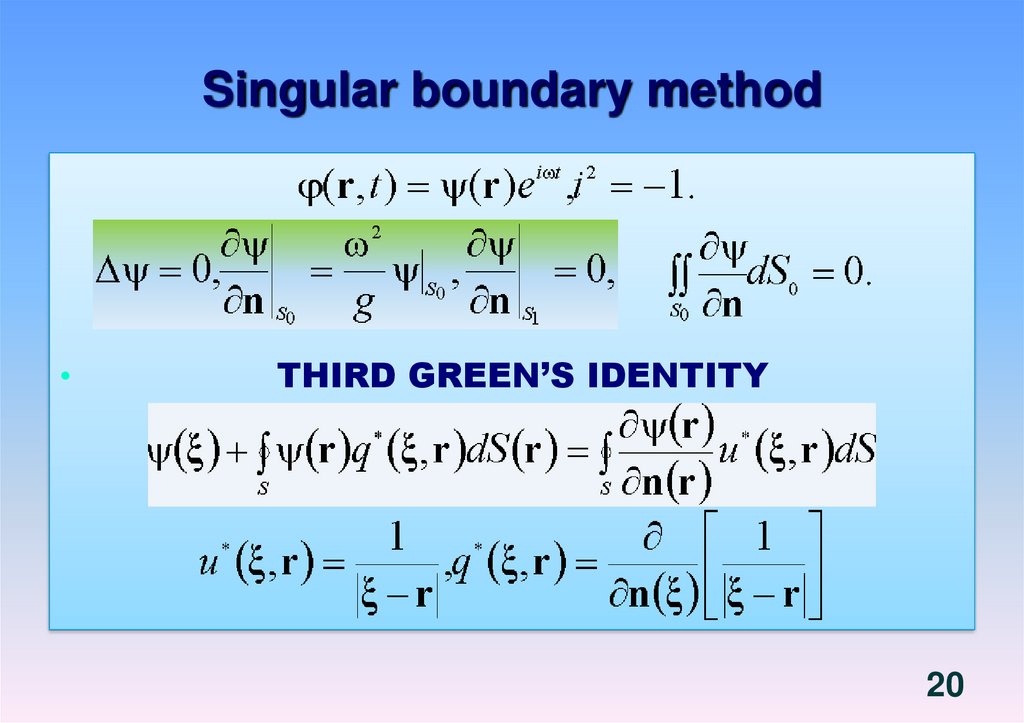
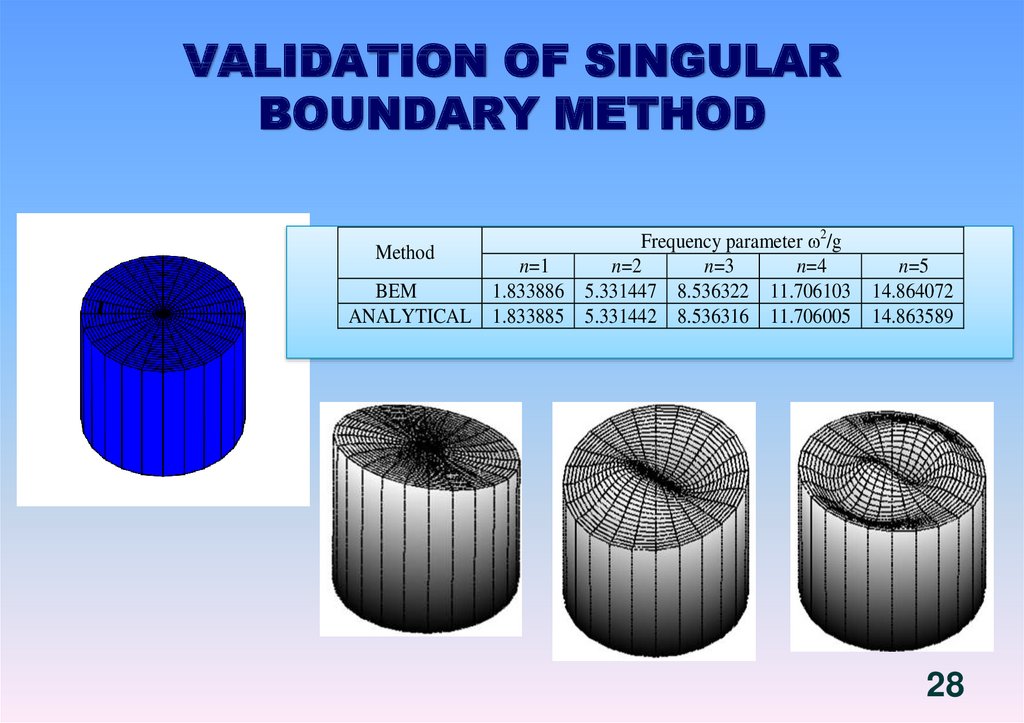
20. Singular boundary method
THIRD GREEN’S IDENTITY
20
21. ONE-DIMENSIONAL BOUNDARY ELEMENTS
2122. Singular boundary method
• We divide boundary into N boundary elements; melements belong to the free surface and others N-m
belong to the shell walls. At each boundary element
we select the collocation point




























 physics
physics industry
industry








