Similar presentations:
Свойства элементарных функций
1. Свойства элементарных функций
10Y
9
8
Алгебра
7
6
5
4
3
2
1
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0
-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
X
1
2
3
4
5
6
7
8
9 10
2. Алгоритм описания свойств функций
СВОЙСТВА ФУНКЦИИАлгоритм описания свойств функций
Область определения
Область значений
Четность
Монотонность
Непрерывность
Ограниченность
Наибольшее и наименьшее значения
Нули функции
Выпуклость
3. Рассмотрим свойства функций:
СВОЙСТВА ФУНКЦИЙРассмотрим свойства функций:
4. Свойства функции y = kx + m (k ≠ 0)
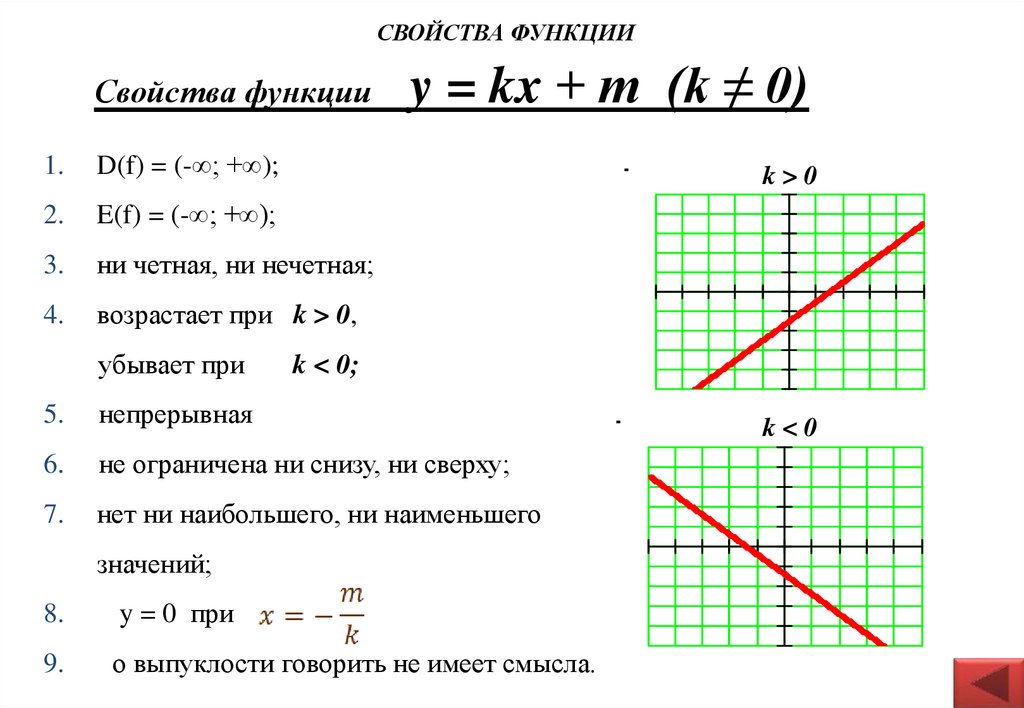
СВОЙСТВА ФУНКЦИИСвойства функции
1.
D(f) = (-∞; +∞);
2.
E(f) = (-∞; +∞);
3.
ни четная, ни нечетная;
4.
возрастает при k > 0,
убывает при
y = kx + m (k ≠ 0)
k>0
k < 0;
5.
непрерывная
6.
не ограничена ни снизу, ни сверху;
7.
нет ни наибольшего, ни наименьшего
значений;
8.
y = 0 при
9.
о выпуклости говорить не имеет смысла.
k<0
5. Свойства функции у = kх2
СВОЙСТВА ФУНКЦИИСвойства функции
у = kх2
при k <
>0
1.
D(f) = (-∞, +∞);
2.
E(f) = (-∞,
Е(f)
[0, +∞);
0];
3.
четная;
четная
4.
убывает на луче (-∞,
[0,+∞),
0],
возрастает на луче [0,
(-∞,
+∞);
0];
5. непрерывна;
непрерывна;
6.
ограничена
не ограничена
снизу,
снизу,
не ограничена
ограничена сверху;
сверху;
7.
унаиб не
= 0,
существует,
унаим не существует;
унаим = 0;
8.
y = 0 при х = 0
9.
выпукла вверх.
вниз.
6. Функция у = ах2 + bх + с
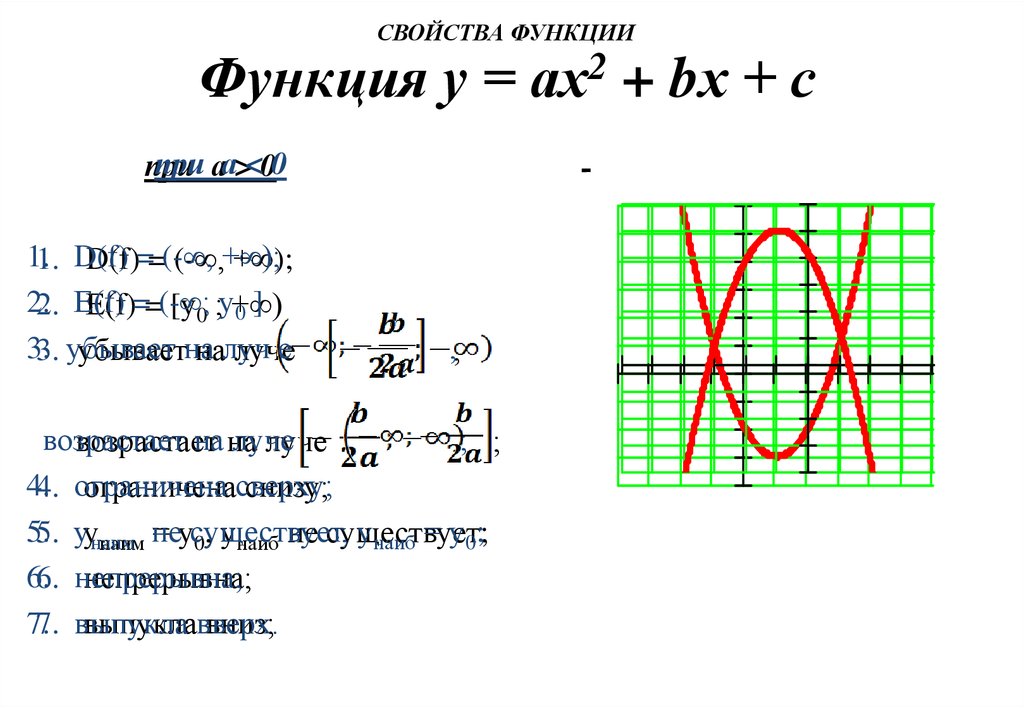
СВОЙСТВА ФУНКЦИИФункция у = ах2 + bх + с
при аа><00
при
1.1. D(f)
D(f)==(-∞,
(-∞,+∞);
+∞);
2.2. Е(f)
Е(f)==(-∞;
[у0 ;у+∞)
0]
3.3. убывает
е
убываетна
налуч
луче
,,
возрастает
на на
луче
; ;
возрастает
луче
4.4. ограничена
ограниченасверху;
снизу;
5.5. уунаим
унаиб = у0;
= усуществует,
наим не
0, унаиб не существует;
6.6. непрерывна;
непрерывна;
7.7. выпукла
выпуклавверх.
вниз;
7. Свойства функции
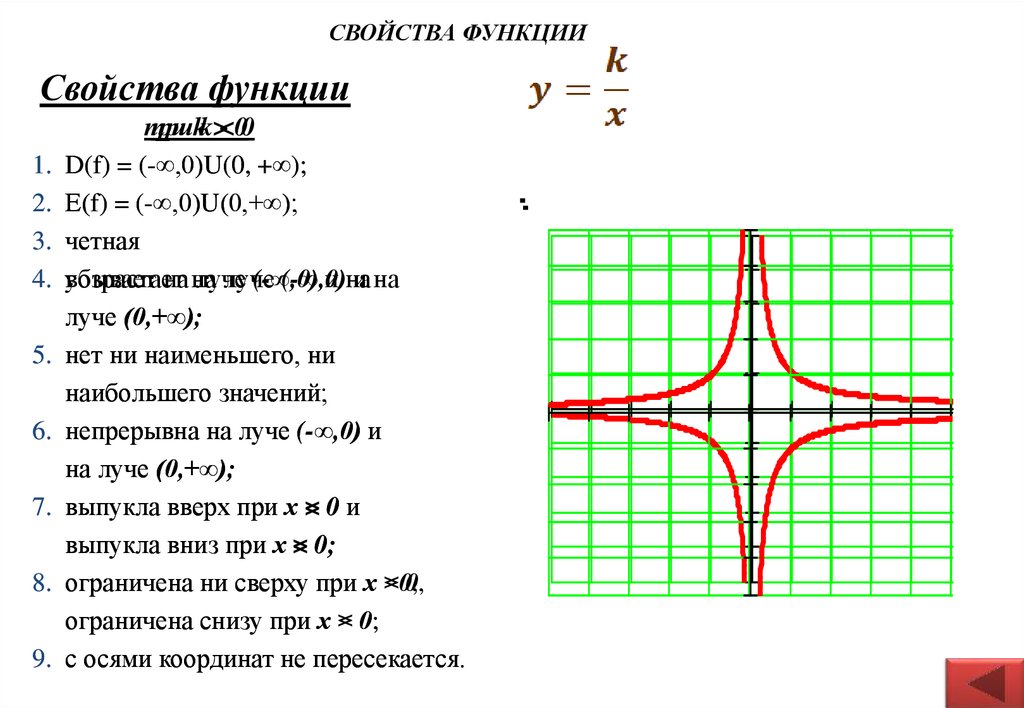
СВОЙСТВА ФУНКЦИИСвойства функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
при
приkk><00
D(f) = (-∞,0)U(0, +∞);
Е(f) = (-∞,0)U(0,+∞);
четная
убывает на на
возрастает
луче
луче
(-∞,0)
(-∞,0)
и на
и на
луче (0,+∞);
нет ни наименьшего, ни
наибольшего значений;
непрерывна на луче (-∞,0) и
на луче (0,+∞);
выпукла вверх при х >
<0и
выпукла вниз при х <
> 0;
ограничена ни сверху при х >0,
< 0,
ограничена снизу при х <
> 0;
с осями координат не пересекается.
8. Функция
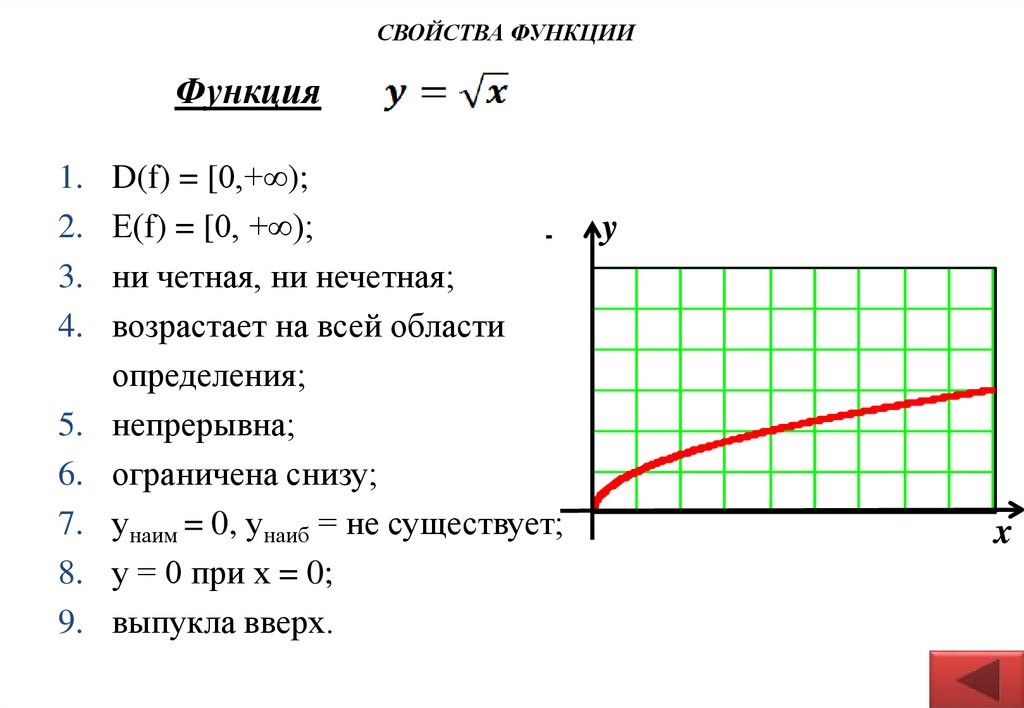
СВОЙСТВА ФУНКЦИИФункция
1.
2.
3.
4.
5.
6.
7.
8.
9.
D(f) = [0,+∞);
Е(f) = [0, +∞);
ни четная, ни нечетная;
возрастает на всей области
определения;
непрерывна;
ограничена снизу;
унаим = 0, унаиб = не существует;
у = 0 при х = 0;
выпукла вверх.
y
x
9. Функция у = |х|
СВОЙСТВА ФУНКЦИИФункция у = |х|
1.
D(f) = (-∞,+∞);
2.
Е(f) = [0, +∞);
3.
четная;
4.
убывает на луче (-∞,0],
возрастает на луче [0, +∞);
5.
непрерывна;
6.
ограничена снизу, не ограничена сверху;
7.
унаим = 0, унаиб не существует;
8.
у = 0 при х = 0;
9.
можно считать выпуклой вниз.





 mathematics
mathematics








