Similar presentations:
Решение задач с помощью квадратных уравнений
1. Здравствуйте !
2. Решение задач с помощью квадратных уравнений
Квадратные уравнения – это фундамент, накотором покоится величественное здание
алгебры. Квадратные уравнения находят широкое
применение при решении различных задач.
Ф. Виет
3.
Великий, немецкийученый А. Эйнштейн
говорил о себе:
«Мне приходится делить своё
время между политикой и
уравнениями. Однако уравнения,
по-моему, гораздо важнее,
потому что политика существует
только до данного момента, а
уравнения будут существовать
вечно».
4. Цели урока:
Совершенствовать навыки составленияуравнения по условию задачи;
Закреплять навыки решения квадратных
уравнений;
Развивать логическое мышление учащихся.
5. Проверка домашнего задания:
№ 547 (а)– 11х = 11; / . 2
НОЗ = 2
∙ 2– 11х ∙ 2 = 11 ∙ 2;
х2 – 1 – 22х = 22;
х2 – 22х – 23 = 0;
D= (b)2 – 4ac = (- 22)2 – 4 ∙ 1 ∙ ( - 23) = 484 + 92 = 576 > 0;
х1 =
=
=
= - 1;
х2 =
=
Ответ: х1 = - 1; х2 = 23.
=
= 23;
6.
№ 558 (а)у = 7х – 1 и у=2х;
7х – 1 = 2х;
7х – 2х = 1;
5х = 1;
х=1 : 5;
х = 0,2;
у=2х = 2 ∙0,2 = 0,4.
Ответ: точка пересечения (0,2; 0,4).
7. Устный счет
8. самопроверка
СПАСИБО1 2 3 4 5 6 7 8 9 10
Поставьте оценку: за 10– « 5»
8-9 – « 4»
5-7- « 3»
0-4 – « 2»
9. Актуализация опорных знаний
2ах
+ bх + с = 0
Квадратное уравнение
10. Всегда ли имеет корни квадратное уравнение?
Нет, не всегда11. От чего зависит количество корней?
От дискриминанта12.
Сколько корней имеет квадратноеуравнение, если D > 0 ?
два
Сколько корней имеет квадратное
уравнение, если D = 0 ?
один
Сколько корней имеет квадратное
уравнение, если D < 0 ?
Нет корней
13. формулы
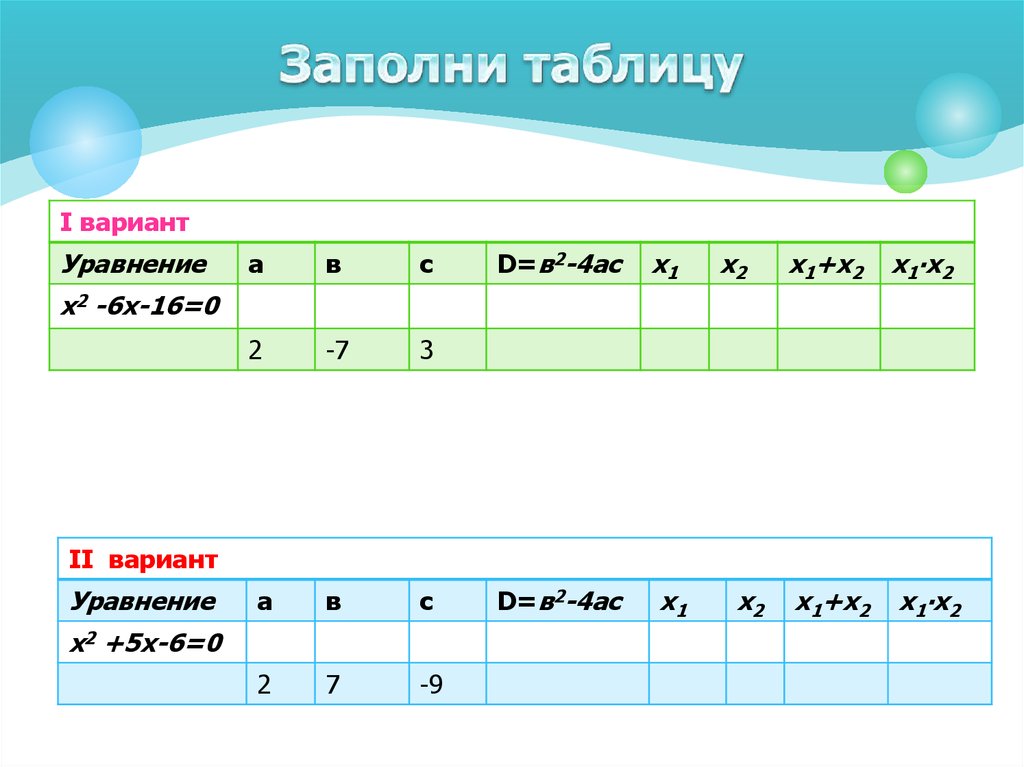
14. Заполни таблицу
I вариантУравнение
а
в
с
2
-7
3
а
в
с
2
7
-9
D=в2-4ас
х1
х2
х1+х2
х1∙х2
х1+х2
х1∙х2
х2 -6х-16=0
II вариант
Уравнение
х2 +5х-6=0
D=в2-4ас
х1
х2
15. Проверим?
I вариантУравнение
а
в
с
D=в2-4ас
х1
х2
х1+х2
х1∙х2
х2 -6х-16=0
1
-6
-16
100
8
-2
6
-16
2х2-7х+3=0
2
-7
3
25
3
0,5
3,5
1,5
II вариант
Уравнение
а
в
с
D=в2-4ас х1
х2
х1+х2
х1∙х2
х2 +5х-6=0
1
5
-6
49
1
-6
-5
-6
2х2+7х-9=0
2
7
-9
121
1
-4,5 3,5
Оцените друг друга:
Оценка «5» если нет
ошибок
«4» если 1-3 ошибки
«3» если ошибок 4-7
-4,5
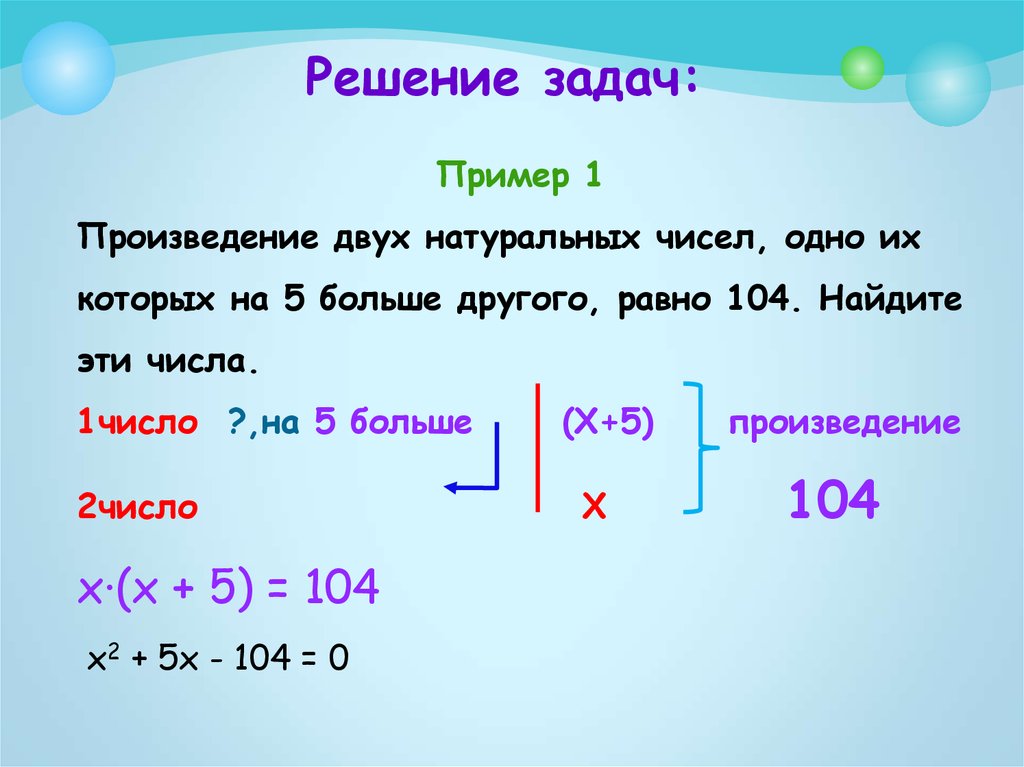
16. Решение задач:
Пример 1Произведение двух натуральных чисел, одно их
которых на 5 больше другого, равно 104. Найдите
эти числа.
1число ?,на 5 больше
2число
х∙(х + 5) = 104
х2 + 5х - 104 = 0
(Х+5)
Х
произведение
104
17.
Решим это квадратное уравнение:х2 + 5х - 104 = 0;
D= (b)2 – 4ac = 52 – 4 ∙ 1 ∙ ( - 104) = 25 + 416 = 441 > 0;
х1 =
х2 =
=
=
= - 13;
= 8;
Первый корень по смыслу задачи не подходит, т.к.
даны натуральные числа. Итак, меньшее число
равно 8, тогда большее число равно 8 + 5 = 13.
Ответ: 8 и 13.
18.
Пример 2В прямоугольном треугольнике один катет больше
другого на 7 см, а гипотенуза больше меньшего
катета на 8 см. Найти стороны треугольника.
А
АВ- ? на 7см больше
х+7
ВС-?
х
АС-? на 8см больше
В
С
х+8
19.
(х + 8)2 = х2 + (х + 7)2х2 + 16х + 64 = х2 + х2 +14х + 49
2
-х
+ 2х + 15 = 0.
20.
Решаем это квадратное уравнение и находимкорни:
х1 = - 3; х2 = 5.
По смыслу задачи значение х должно быть
положительным числом. Поэтому подходит
только второй корень х = 5 – длина меньшего
катета.
5 + 7 = 12 см – длина большего катета;
5 + 8 = 13 см – длина гипотенузы.
Ответ: 5 см, 12 см, 13 см.
21. Тренировочные упражнения
1. Составьте уравнение к задаче, приняв за хменьшее из чисел.
Одно из чисел на 12 больше другого, а их
произведение равно 315. Найдите эти числа.
1) х (х – 12) = 315
2) х (х + 12) = 315
3) 2х + 12 = 315
4) 2х – 12 = 315
22.
2. Найдите катеты прямоугольного треугольника,если один из них на 7 см меньше другого, а
гипотенуза равна 17 см.
1) 10см и 17 см
2) 8см и 15 см
3) 16 см и 9 см
4) 8 см и 6 см.
23. Подведение итогов. Рефлексия.
Что мы сегодня повторили на уроке?А что нового мы с вами сегодня узнали
на уроке?
Какой этап урока вам понравился больше
всего?
Кто доволен своей работой сегодня?
24.
Спасибо за урок!Всем удачи!






















 mathematics
mathematics








