Метод интервалов

1. Метод интервалов

Подготовила:
учитель математики
МОУ сош №30 имени А.И.Колдунова
Кутоманова Е.М.
2010-2011 учебный год

2. Рассмотрим функцию f(х)=(х+3)(х-1)(х-2).

D(f)- любое число,
нули функции- числа -3; 1; 2.
Нули функции разбивают всю область определения
на промежутки: (-∞;-3),(-3;1),(1;2), (2;∞).
Выясним, какой знак имеет функция на каждом из
указанных промежутков:
f(-4)=-1·(-5)(-6)=-30<0;
f(0)=3·(-1)·(-2)=6>0;
f(1,5)=4,5·0,5·(-0,5)<0;
f(3)=6·2·1>0;
+
-3
1
+
2
f
х

3.

ТЕОРЕМА :Если функция f непрерывна на
интервале (a;b) и не обращается в 0 на
этом интервале, то f сохраняет на нём
постоянный знак.
Необходимым условием смены знака в точке С является : f (c)=0
Однако , это не является достаточным условием : функция f
может и не менять своего знака при переходе через точку С

4.

Методом интервалов можно решать неравенства вида:
f(х)>0 ,
f(х) 0
f(х)<0 ,
f(х) 0

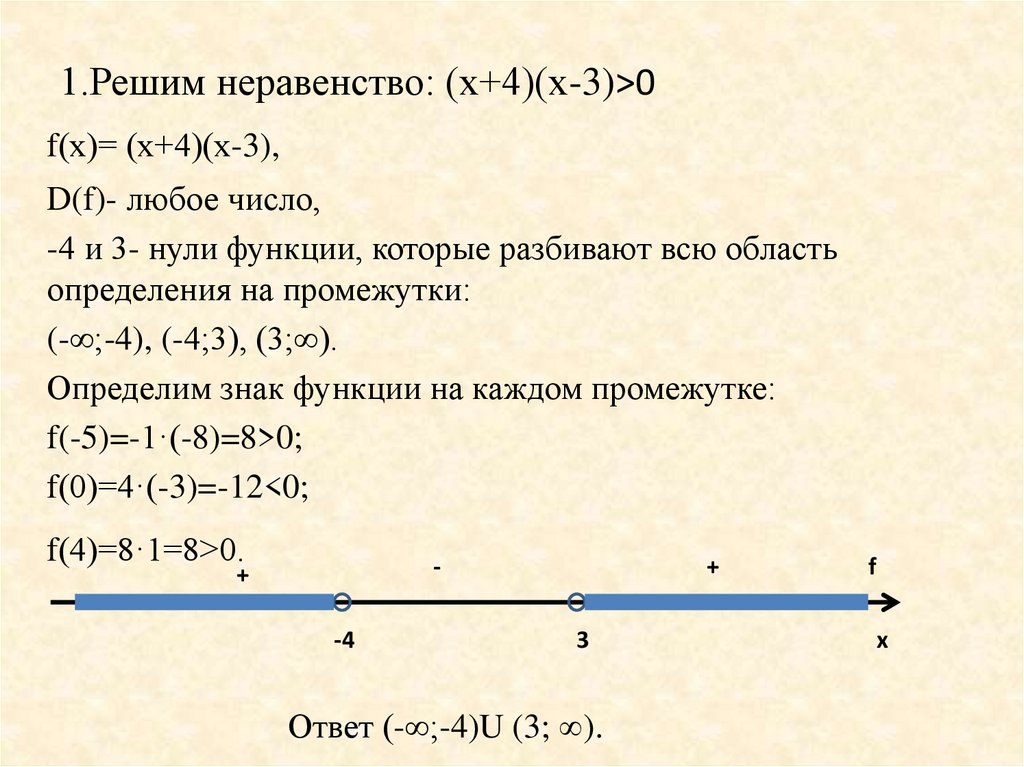
5. 1.Решим неравенство: (х+4)(х-3)>0

1.Решим неравенство: (х+4)(х-3)>0
f(х)= (х+4)(х-3),
D(f)- любое число,
-4 и 3- нули функции, которые разбивают всю область
определения на промежутки:
(-∞;-4), (-4;3), (3;∞).
Определим знак функции на каждом промежутке:
f(-5)=-1·(-8)=8>0;
f(0)=4·(-3)=-12<0;
f(4)=8·1=8>0.
-
+
-4
+
3
Ответ (-∞;-4)U (3; ).
f
х

6. 2.Решим неравенство: (х+5)(х+1)(х-3)<0.

2.Решим неравенство: (х+5)(х+1)(х-3)<0.
f(х)=(х+5)(х+1)(х-3),
D(f)-любое число,
-5;-1;3- нули функции, которые разбивают всю область
определения на промежутки:
(-∞;-5), (-5;-1), (-1;3).(3;∞).
Определим знак функции на каждом промежутке:
f(-6)=-1·(-5)·(-9)=-45<0,
f(-2)=3·(-1)·(-5)=15>0,
f(0)=5·1·(-3)=-15<0,
f(4)=9·5·6=270>0.
+
-5
-
-1
Ответ (-∞;-5)U (-1;3).
+
3
f
х

7. №3. Решим неравенство

х 3
0
№3. Решим неравенство
х
5
х 3
f ( x)
х 5
,
D(f)- любое число, кроме -5,
3- нуль функции.
+
+
-5
3
f
х
6 3 9
3
4 3 1
f ( 6)
9 0, f (0)
0, f (4)
0,
6 5 1
5
4 5 9
х 5;3
Ответ : 5;3

8. №4. Решим неравенство

х 3
2
№4. Решим неравенство
х
5
х 3
2
х 5
х 3
2 0
х 5
х 3
2 0
х 5
х 3 2 х 10
0
х 5
х 13
0
х 5
х 13
0
х 5
х 13
f ( x)
,
х 5
D(f)- любое число, кроме -5,
-13-нуль функции.
+
-
-13
f ( 14)
1
0,
9
f ( 6)
х ; 13 5;
Ответ : ; 13 5;
+
-5
7
13
0, f (0) 0,
1
5
f
х