Similar presentations:
Система двух линейных уравнений с двумя переменными a1 x b1 y c1 0, a2 x b2 y c2 0
1. Система двух линейных уравнений с двумя переменными
a1 x b1 y c1 0,a2 x b2 y c2 0
2. Решение системы двух линейных уравнений с двумя переменными
Пара значений (Х;У), которая являетсяодновременно решением и первого, и
второго уравнений системы,
называется решением системы.
3. Что значит «решить систему двух линейных уравнений с двумя переменными»?
Решить систему – значит найти все еерешения или установить, что их нет
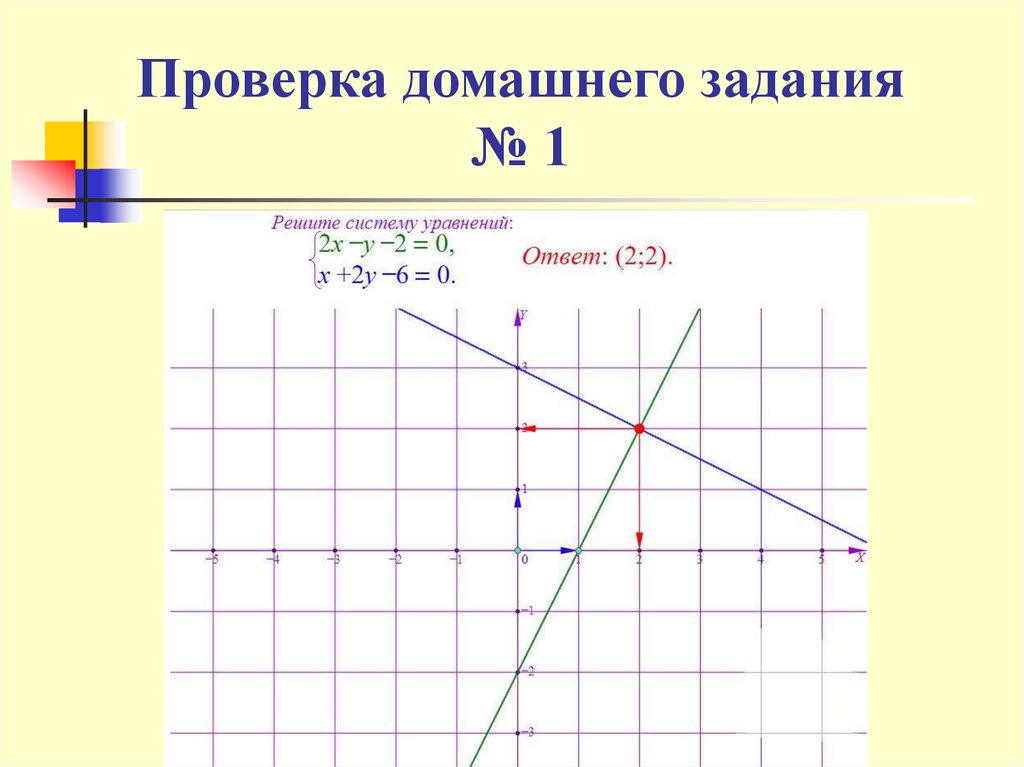
4. Проверка домашнего задания № 1
Проверка домашнего задания№1
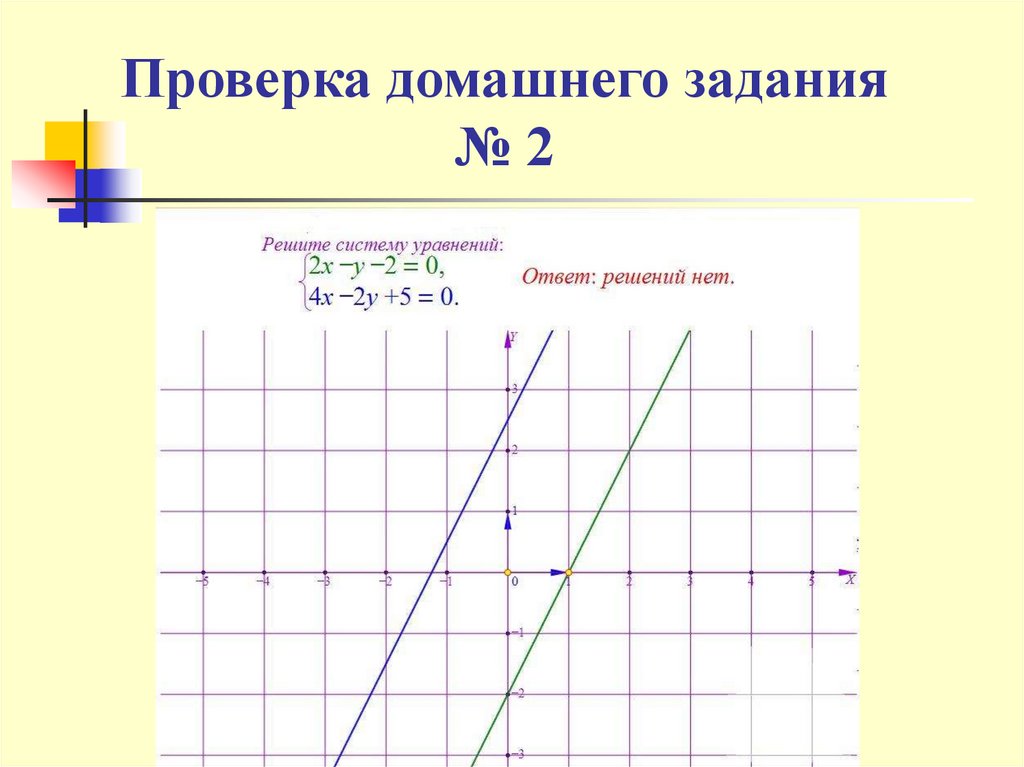
5. Проверка домашнего задания № 2
Проверка домашнего задания№2
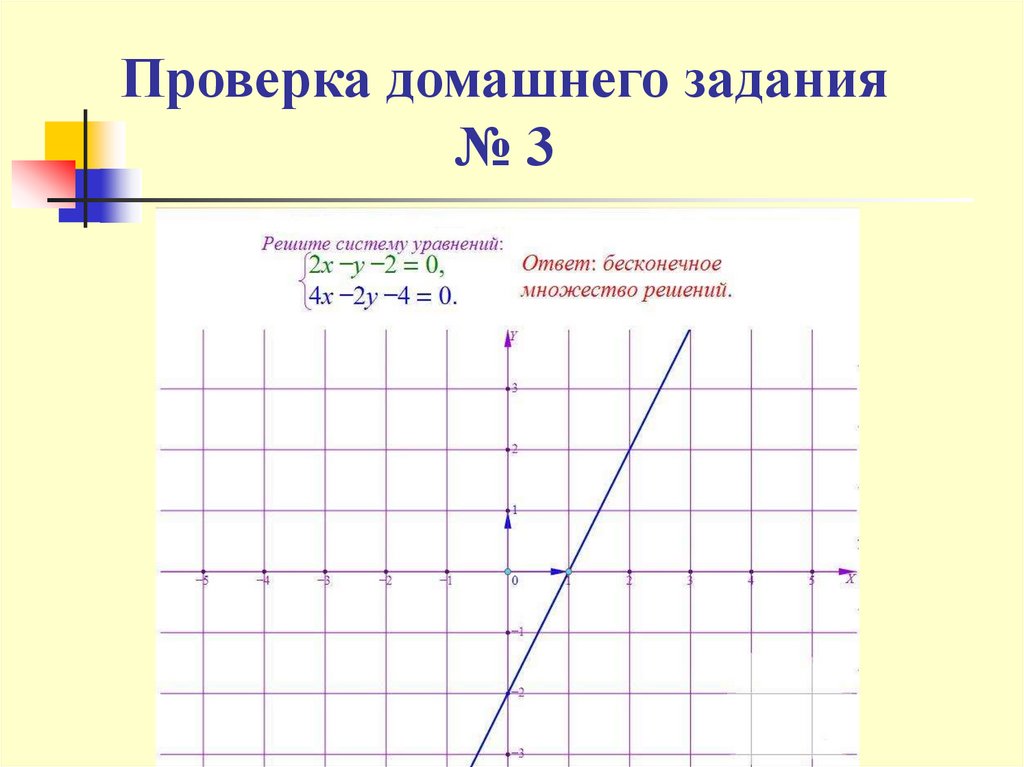
6. Проверка домашнего задания № 3
Проверка домашнего задания№3
7. С помощью графического метода можно сделать важные выводы:
к1С помощью графического метода
можно сделать важные выводы:
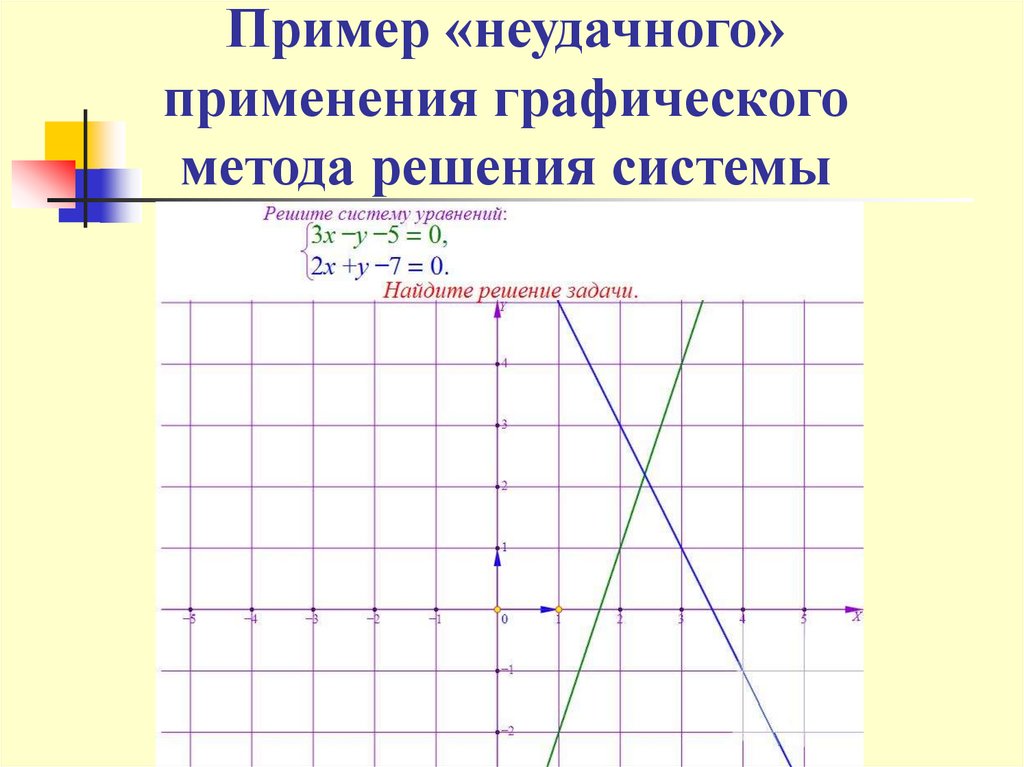
8. Пример «неудачного» применения графического метода решения системы
9. Метод подстановки
10. Алгоритм решения системы двух уравнений с двумя переменными методом подстановки
1. Выразить y через x из первого уравнения системы2. Подставить полученное на первом шаге выражение
вместо y во второе уравнение системы
3. Решить полученное на втором шаге уравнение
относительно x
4. Подставить найденное на третьем шаге значение x в
выражение y через x, полученное на первом шаге
5. Записать ответ в виде пары значений (x;y), которые
были найдены соответственно на третьем и четвертом
шагах
11. Пример «неудачного» применения графического метода решения системы
12. Алгоритм решения системы двух уравнений с двумя переменными методом подстановки
1. Выразить y через x из первого уравнения системы2. Подставить полученное на первом шаге выражение
вместо y во второе уравнение системы
3. Решить полученное на втором шаге уравнение
относительно x
4. Подставить найденное на третьем шаге значение x в
выражение y через x, полученное на первом шаге
5. Записать ответ в виде пары значений (x;y), которые
были найдены соответственно на третьем и четвертом
шагах
13. № 412 (а,б)
14. Домашнее задание
§12Знать алгоритм решения системы методом
подстановки
Самостоятельно разобрать примеры № 1-2
№№ 416, 413, 414(в,г)










 mathematics
mathematics








