Исследование магнитоупругих колебаний в магнитной пленке при сверхбыстром лазерном возбуждении с использованием техники

1. Исследование магнитоупругих колебаний в магнитной пленке при сверхбыстром лазерном возбуждении с использованием техники

«transient grating»
Научный руководитель: К.ф.-м.н., доцент
Власов Владимир Сергеевич
Исполнитель: студент 122 группы
Перовский Игорь Андреевич

2.

Актуальность
Рассматривается
новое
направление
–
сверхбыстрая акустомагнитная оптика. Если
говорить о конкретном применении: то это
контроль намагниченности в короткие сроки
для реализации быстрой магнитной памяти
и маломощной магнитной логики.

3.

Целью работы является расчет магнитоупругих колебаний в
магнитной пленке при сверхбыстром лазерном возбуждении
с использованием техники «transient grating»
Задачи:
Определение параметров упругой волны с применением
техники «transient grating»
Решение задачи о нахождении собственных упругих волн
системы пленка +подложка
Расчет магнитных колебаний возбуждаемых упругими
волнами

4.

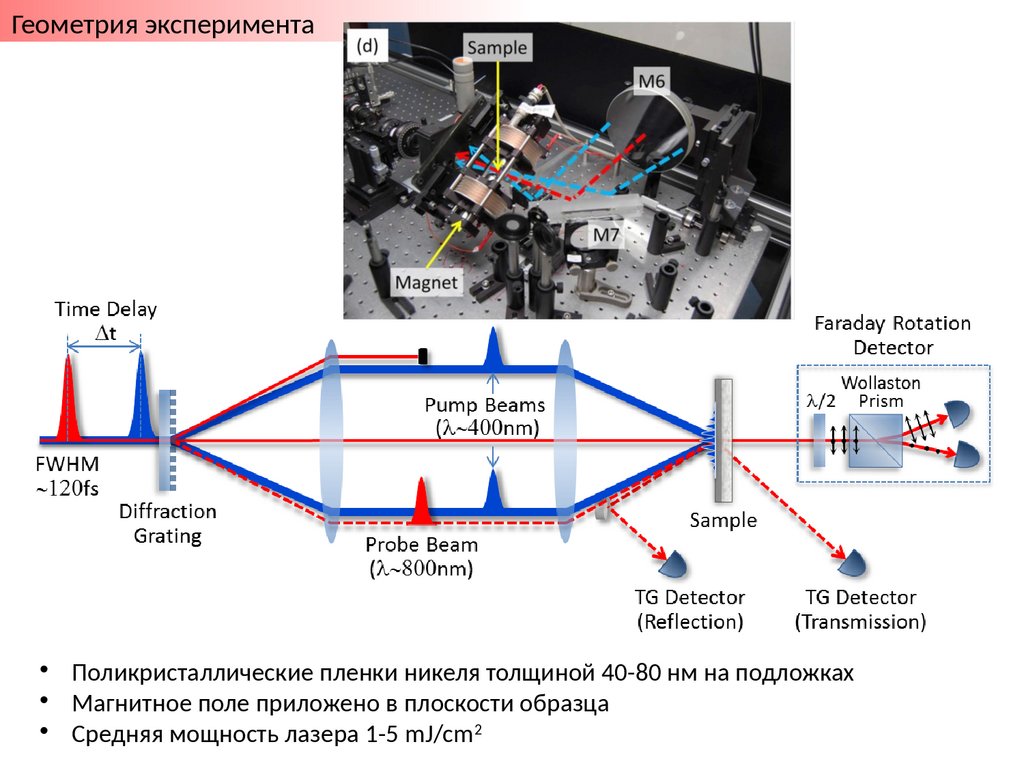
Геометрия эксперимента
• Поликристаллические пленки никеля толщиной 40-80 нм на подложках
• Магнитное поле приложено в плоскости образца
• Средняя мощность лазера 1-5 mJ/cm2

5.

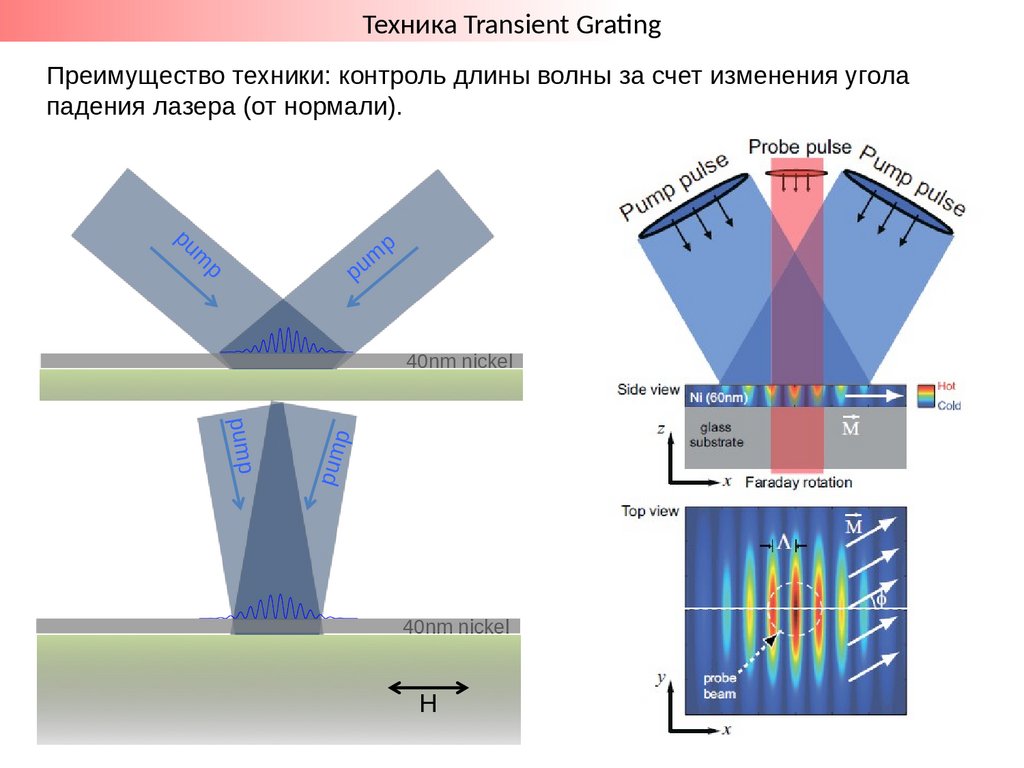
Техника Transient Gratng
Преимущество техники: контроль длины волны за счет изменения угола
падения лазера (от нормали).
m
m
pu
p
p
40nm nickel
pum p
pum
p
pu
H
H
40nm nickel
HH

6.

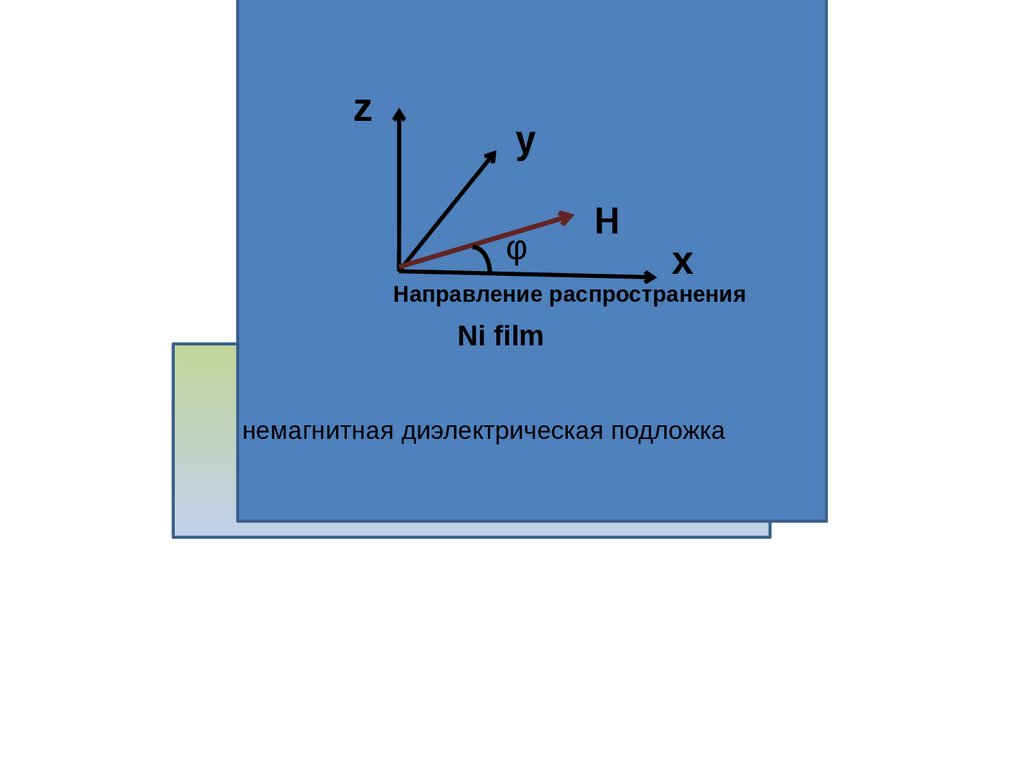
Геометрия задачи
z
y
φ
H
x
Направление распространения
Ni film
немагнитная диэлектрическая подложка

7.

Основные уравнения
mx
0
m y mx mz H eff , z mz m y mx H eff , y m 2y mz2 H eff , x
t
1 2
my
t
0
1
mz m y mx H eff , x mx mz m y H eff , z mz2 mx2 H eff , y
2
0
mz
mx mz m y H eff , y m y mx mz H eff , x mx2 m 2y H eff , z
t
1 2
1
F
H eff ,i
0 M 0 mi

8.

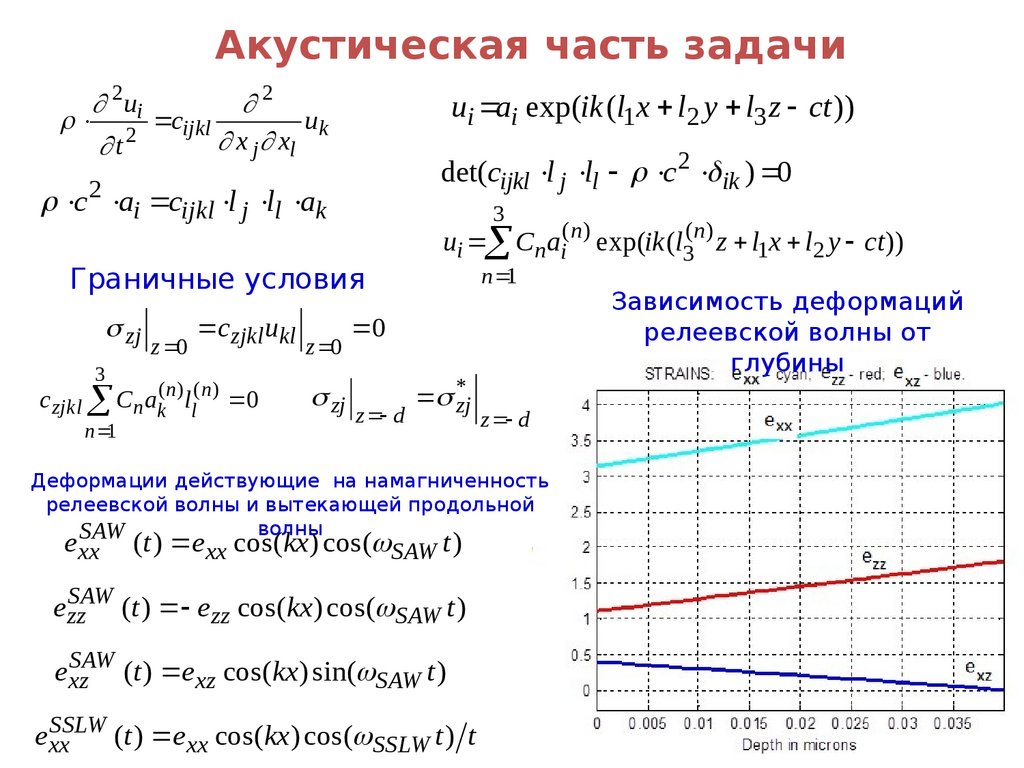
Акустическая часть задачи
2ui
2
2 сijkl
uk
x j xl
t
ui ai exp(ik (l1x l2 y l3 z ct ))
det(сijkl l j ll c 2 ik ) 0
c 2 ai сijkl l j ll ak
3
Граничные условия
zj
z 0
с zjklukl
z 0
n 1
zj
n 1
0
3
c zjkl Cn ak( n)ll( n) 0
ui Cn ai( n) exp(ik (l3( n) z l1x l2 y ct ))
z d
*zj
z d
Деформации действующие на намагниченность
релеевской волны и вытекающей продольной
волны
SAW
exx
(t ) e xx cos(kx) cos( SAW t )
SAW
ezz
(t ) ezz cos(kx) cos( SAW t )
SAW
exz
(t ) e xz cos(kx ) sin( SAW t )
SSLW
exx
(t ) exx cos(kx ) cos( SSLW t ) t
Зависимость деформаций
релеевской волны от
глубины

9.

Магнито-акустические динамики при малых
углах φ
m x 1
m y m yd
m z m zd
0
yd 2 m yd Dm yd exz (t ) Ae xz (t ) Bexx (t )
m
2 2b1 0
2 2
0 H ( H M 0 )
( H ezz (t ) ( 2 H M 0 )e xx (t ))
M0
2 2 b1 0
4 b2
2 b2
D
A
B
(H M 0 )
M0
M0
M0
2
Ae xz (t ) Bexx (t ) 0
0
SAW
b2
0 ( H M 0 ) b1
H 1.6 104 A m
exz
exx
4 b2
e xz (t )
M0
This condition we can realize for SAW
exz
0.07
exx
M 0 4.8 105 A m
b1 b2
1.1 m
0 1

10.

Магнитоакустическая динамика при
произвольных углах φ
2b 1
H eff , z M 0 mz
H eff , x H cos
mx exx (t ) H eff , y H sin
0 M 0
m z m zd
m x cos m xd m y sin m yd
0
m xd
(m zd sin ( H M 0 ) H sin (m yd cos m xd sin )
2
1
2b1
exx cos sin 2 M 0 m yd m zd )
0 M 0
0
m yd
(m zd cos ( H M 0 ) H cos (m yd cos m xd sin )
2
1
2b1
exx ( cos 2 sin m zd cos ) M 0 m xd m zd )
0 M 0
0
m zd
( H ( m xd sin m yd cos ) m zd ( H M 0 )
2
1
2b1
exx (cos sin m yd cos m xd sin ))
0 M 0
Линейный случай 0
b
m zd r2 m zd 1 e xx sin 2
M0
maximum interaction
angle
max 45

11.

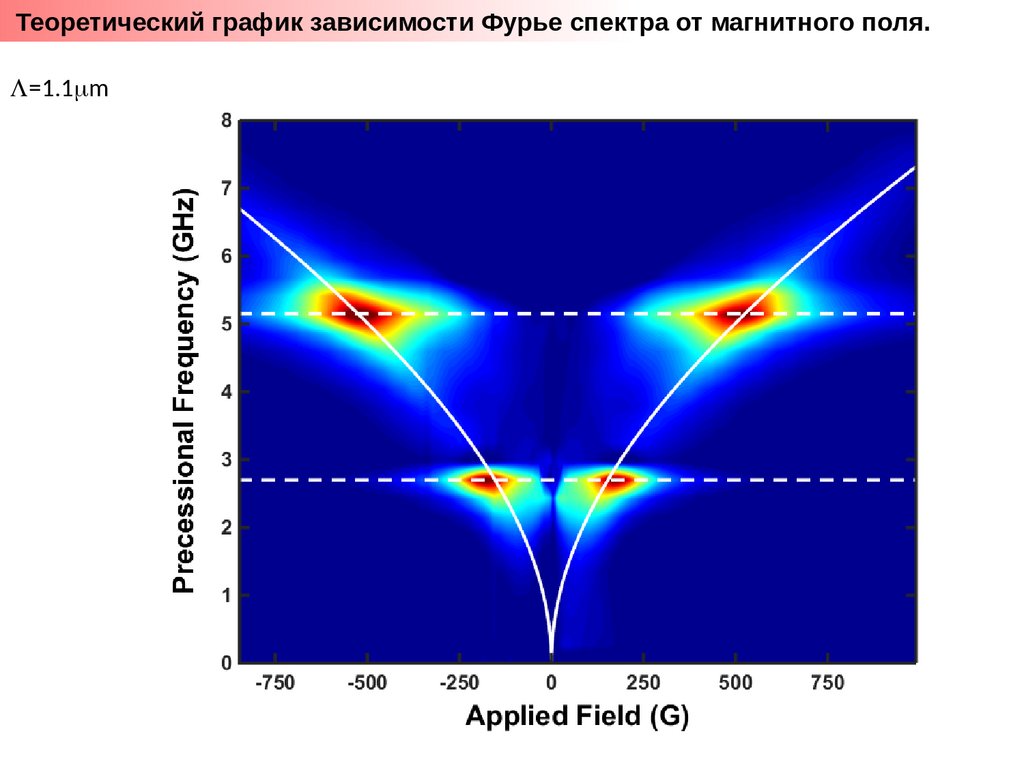
Теоретический график зависимости Фурье спектра от магнитного поля.
L=2μm
L=1.1 m

12.

Нелинейное взаимодействие упругих волн с
магнитным генератором
L = 1.4 m
Эксперимент
SSLW
SAW
Теория

13. Выводы