Similar presentations:
Окружность. Электронное пособие для учащихся 2012 год
1. ОКРУЖНОСТЬ
Электронное пособие для учащихся2012 год
ОКРУЖНОСТЬ
Данное пособие поможет представить
изучаемый материал по теме: «Окружность»
и поможет систематизировать свои знания.
Разработали учащиеся 11 «А» класса МБОУ СОШ № 15 г.Королёва
Сергиенко Владислав и Челыхов Михаил под руководством
учителей Диановой В.А. и Моисеевой В.И.
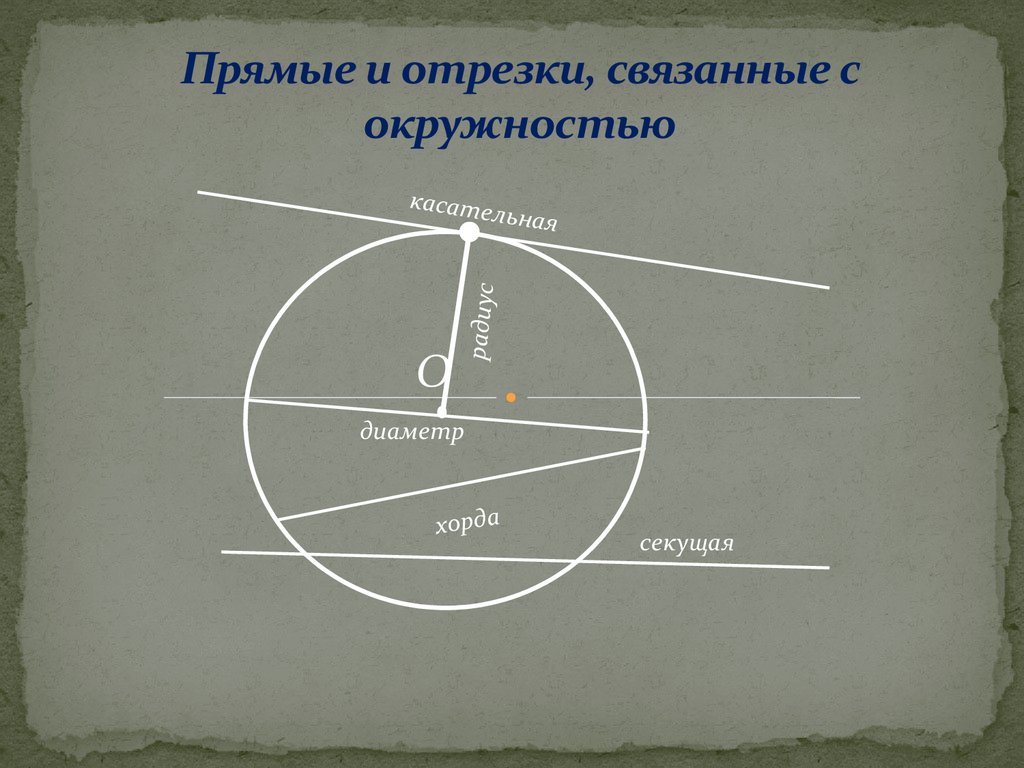
2. Прямые и отрезки, связанные с окружностью
Орадиус
касате
льная
диаметр
хорда
секущая
3. Углы, связанные с окружностью угловая мера дуги окружности
вписанныйвпис
анны
й
центральный
центральный
центральный
центральный
Угловой мерой дуги окружности является центральный угол,
который опирается на эту лугу
4. Радианная мера угла
Угол в один радиан равен центральному углу, опирающемуся надугу, длина которой равна радиусу окружности.
1 радиан ≈ 57⁰17’45”,
O
н
иа
ад
1р
R
1
радиан
180
π радиан = 180⁰,
π
радиан
2
90 .
5. Свойства вписанных углов
βα
Вписанный угол равен половине
центрального, опирающегося на ту же
дугу:
2
Все вписанные углы, опирающиеся на
одну и ту же дугу, равны.
6.
Все вписанные углы,опирающиеся на одну и ту
же хорду, вершины которых
лежат по одну сторону этой
хорды, равны.
α
β
Любая пара углов, опирающихся
на одну и ту же хорду, вершины
которых лежат по разные
стороны хорды, составляют в
сумме 180⁰
180
7.
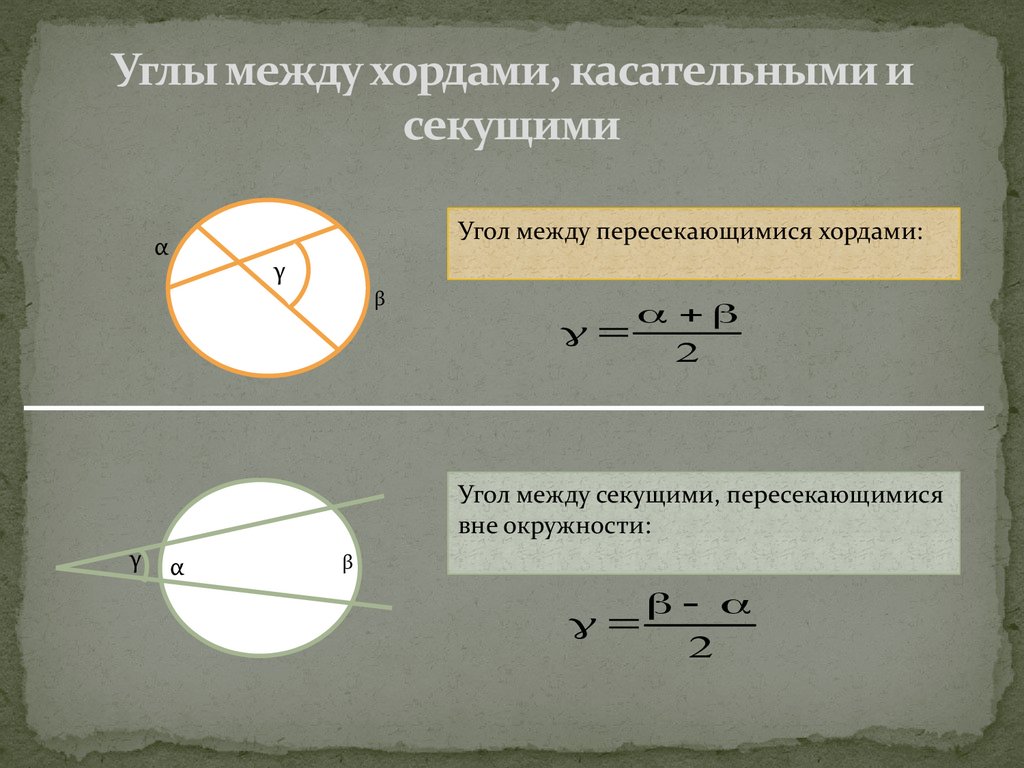
Все вписанные углы, опирающиеся на диаметр, прямые.8. Углы между хордами, касательными и секущими
Угол между пересекающимися хордами:α
γ
β
2
Угол между секущими, пересекающимися
вне окружности:
γ
α
β
2
9.
γУгол между касательной и
секущей:
α
β
2
Угол между касательными:
γ
α
β
2
10.
Угол между касательной и хордой:γ
α
2
11. Свойства хорд
Если хорды равноудалены от
центра окружности, то они равны.
Если хорды равны, то они
равноудалены от центра
окружности.
Большая из двух хорд находится
ближе к центру окружности
12.
Н а и б ол ь ш а я хо рд а я вл я е т с я
диаметром.
Если диаметр делит хорду пополам,
то он перпендикулярен ей.
Если диаметр перпендикулярен
хорде, то он делит её пополам.
13.
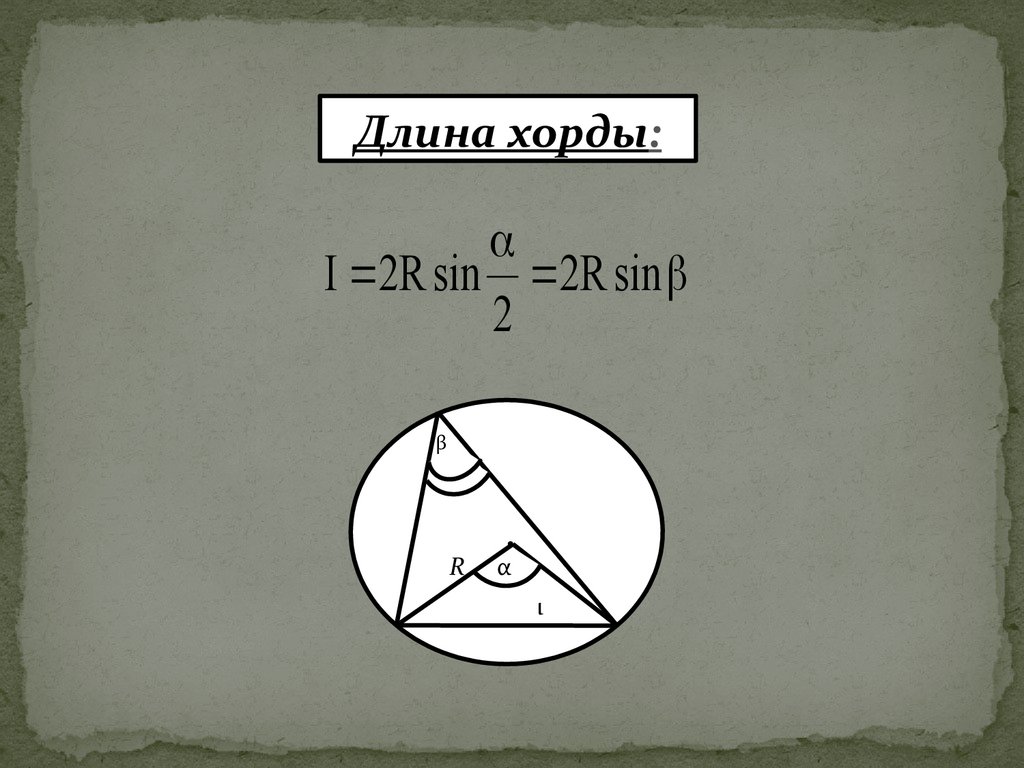
Длина хорды:I 2R sin 2R sin
2
β
R
α
ι
14. Соотношения между длинами хорд, отрезков касательных и секущих
ac
d
b
Отрезки пересекающихся
хорд связаны соотношением:
ab = cd
15.
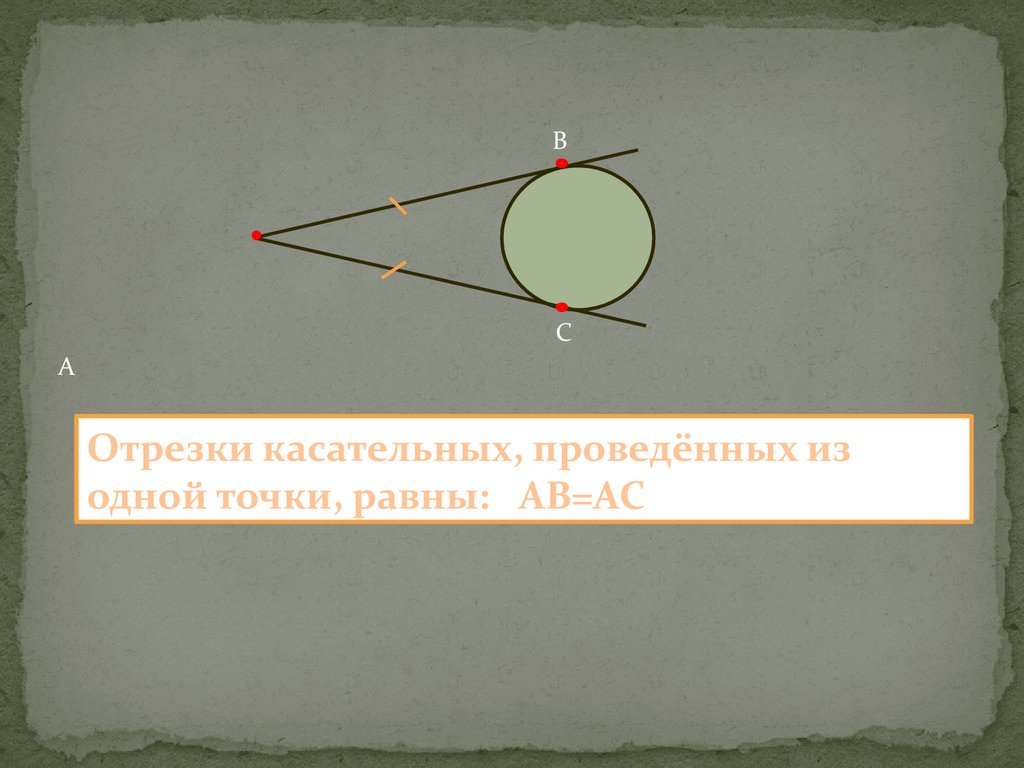
BC
A
Отрезки касательных, проведённых из
одной точки, равны: AB=AC
16.
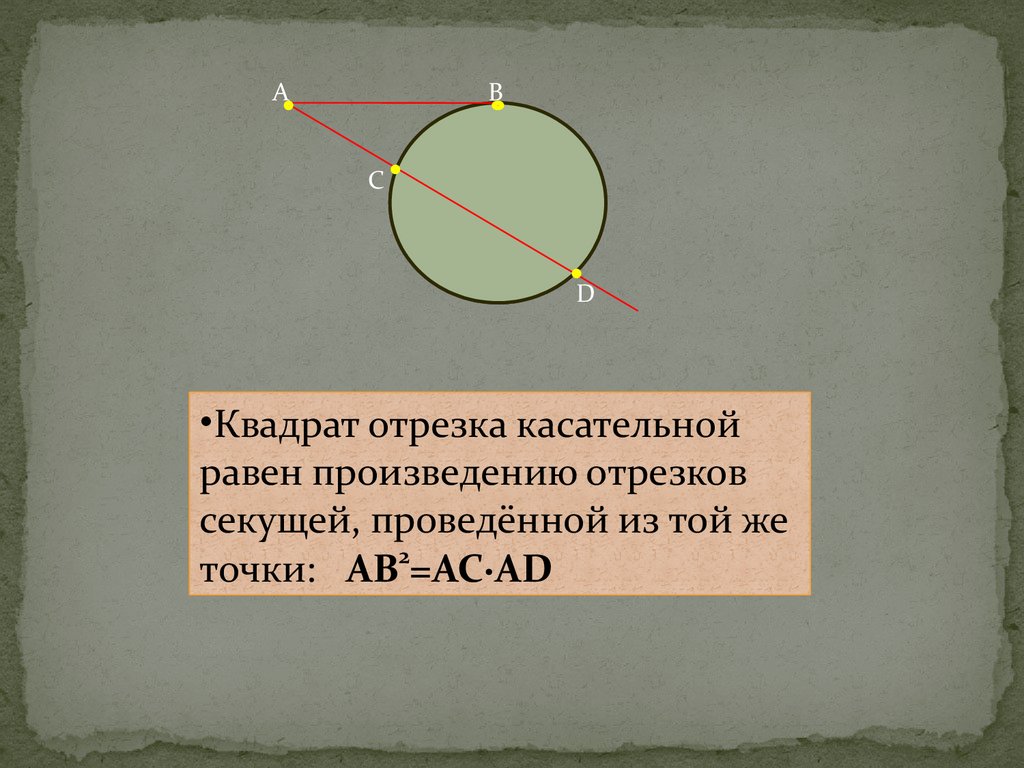
AB
C
D
•Квадрат отрезка касательной
равен произведению отрезков
секущей, проведённой из той же
точки: AB2=AC∙AD







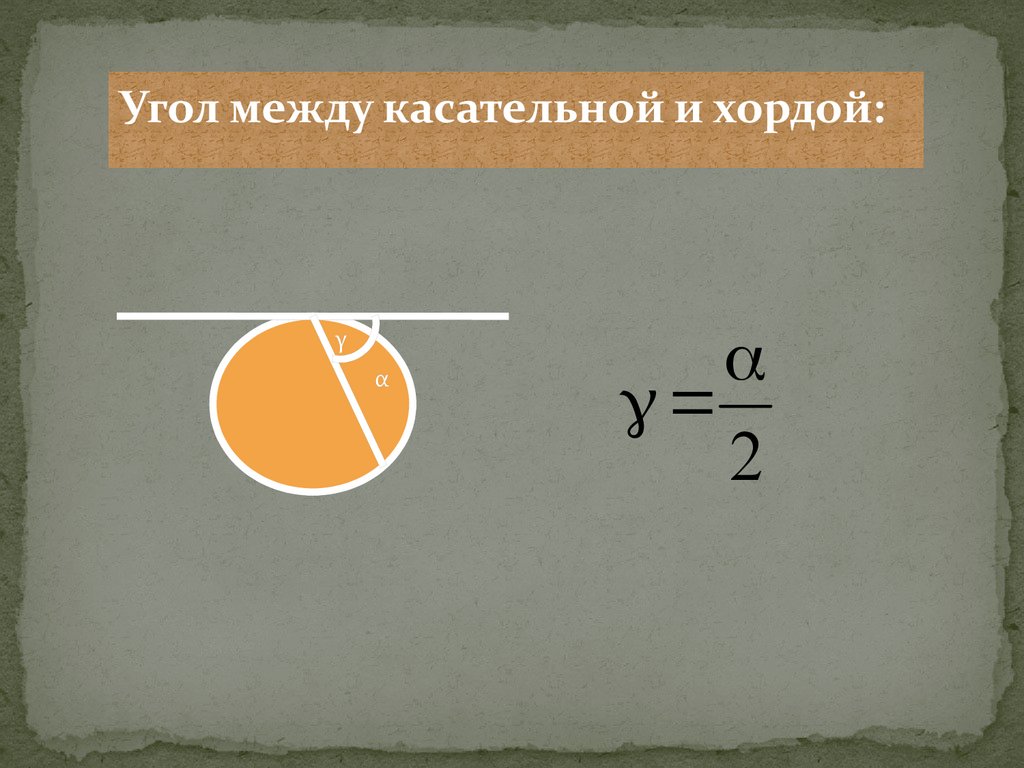




 mathematics
mathematics informatics
informatics








