Similar presentations:
Окружность. Итоговое повторение
1. Итоговое повторение темы:
Окружность2. Содержание :
Взаимное расположение прямой иокружности
Углы, связанные с окружностью.
Свойства вписанных углов.
Свойства отрезков хорд, секущих и
касательных .
Длина окружности и площадь круга.
Вписанная и описанная окружность
Тест.
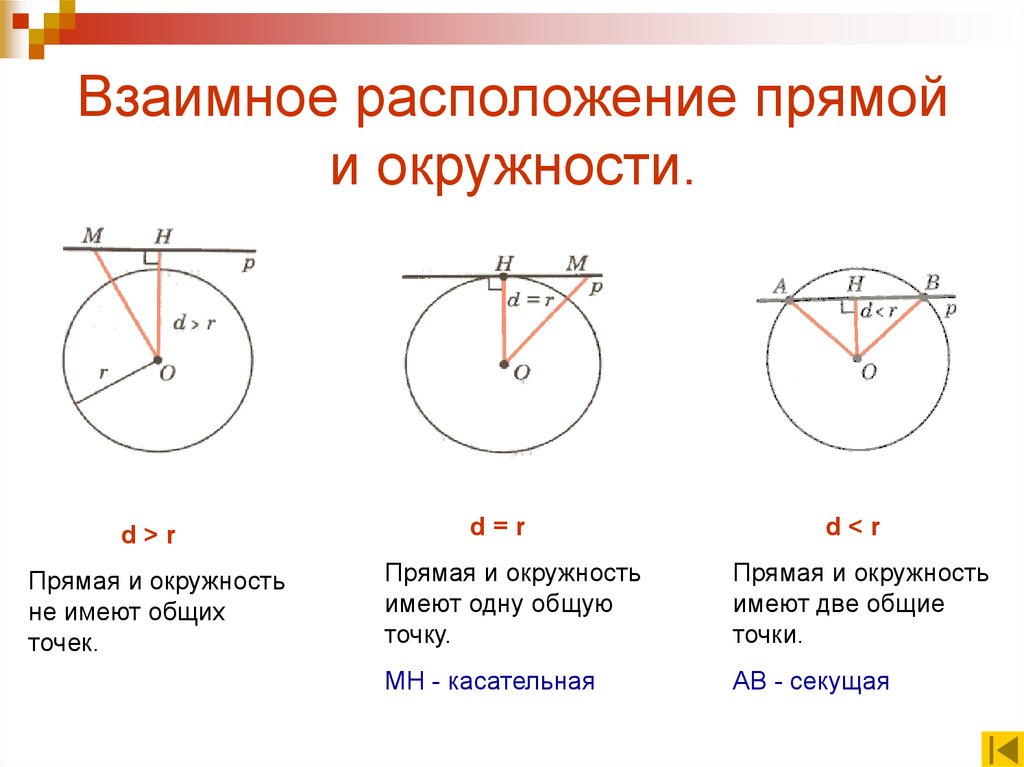
3. Взаимное расположение прямой и окружности.
d>rПрямая и окружность
не имеют общих
точек.
d=r
d<r
Прямая и окружность
имеют одну общую
точку.
Прямая и окружность
имеют две общие
точки.
МН - касательная
АВ - секущая
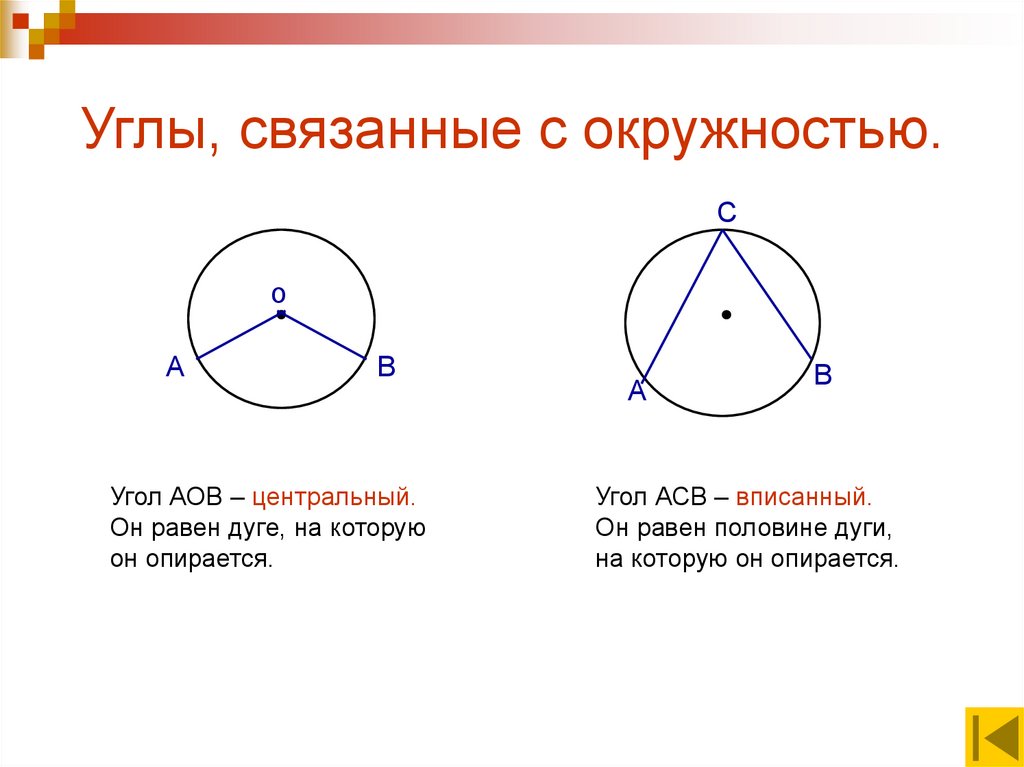
4. Углы, связанные с окружностью.
Со
А
В
Угол АОВ – центральный.
Он равен дуге, на которую
он опирается.
А
В
Угол АСВ – вписанный.
Он равен половине дуги,
на которую он опирается.
5.
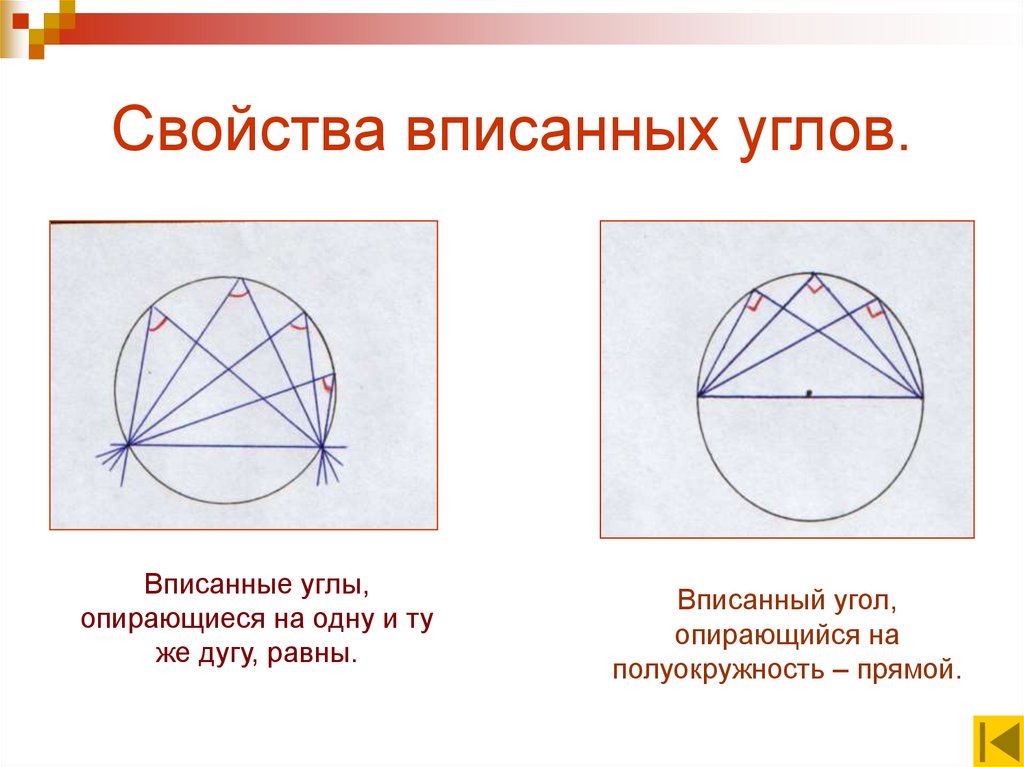
6. Свойства вписанных углов.
Вписанные углы,опирающиеся на одну и ту
же дугу, равны.
Вписанный угол,
опирающийся на
полуокружность – прямой.
7. Свойство отрезков касательных.
АА
В
В
О
Касательная к окружности
перпендикулярна к
радиусу, проведенному в
точку касания.
ОА I AB
С
О
Отрезки касательных к окружности,
проведенные из одной точки,
равны и составляют равные углы с
прямой, проходящей через эту
точку и центр окружности.
AB = AC , ےBAО = ےOAC
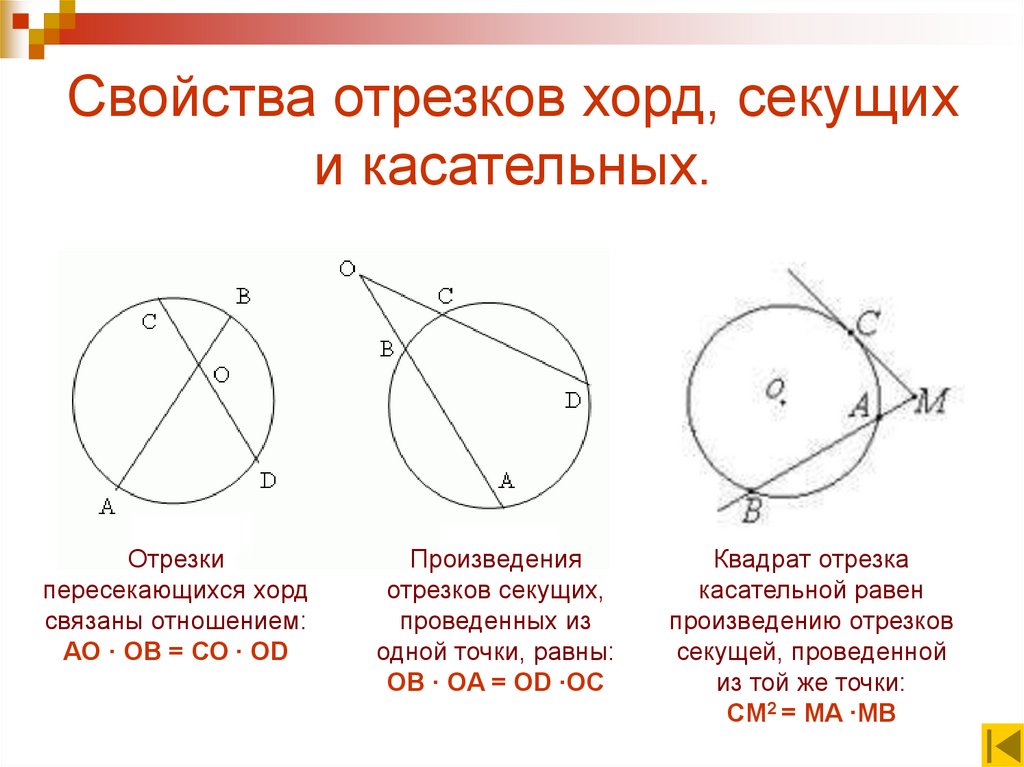
8. Свойства отрезков хорд, секущих и касательных.
Отрезкипересекающихся хорд
связаны отношением:
AO ∙ OB = СО ∙ OD
Произведения
отрезков секущих,
проведенных из
одной точки, равны:
OB ∙ OA = OD ∙OC
Квадрат отрезка
касательной равен
произведению отрезков
секущей, проведенной
из той же точки:
CM2 = MA ∙MB
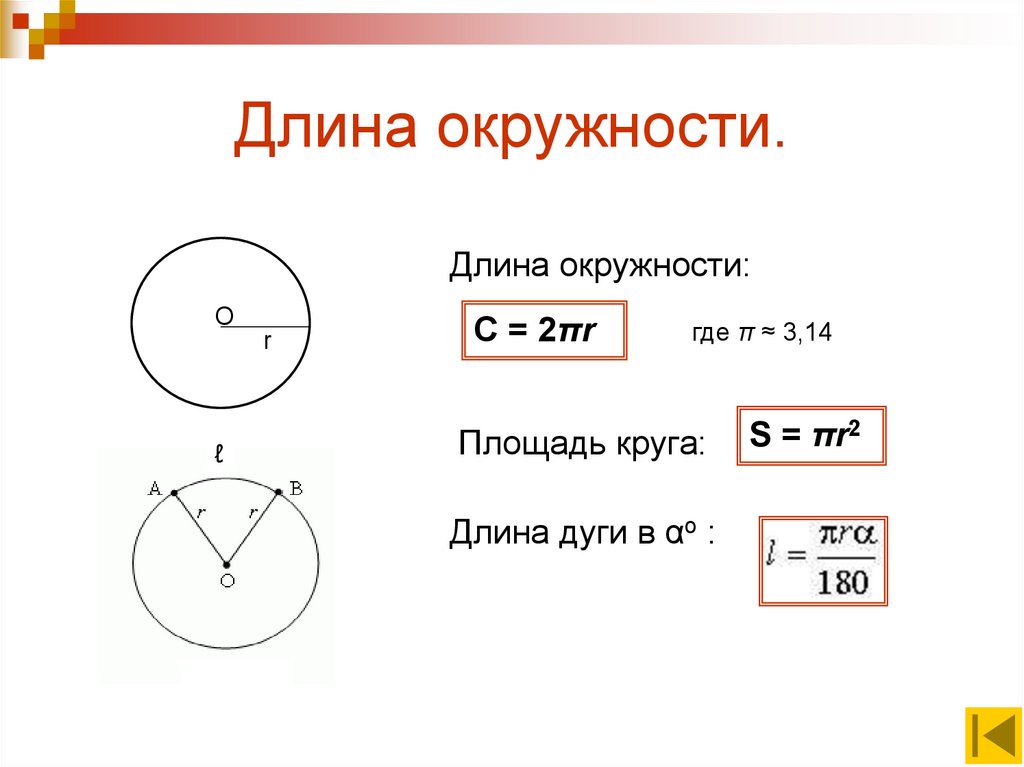
9. Длина окружности.
Длина окружности:О
r
ℓ
C = 2πr
где π ≈ 3,14
Площадь круга:
Длина дуги в αo :
S = πr2
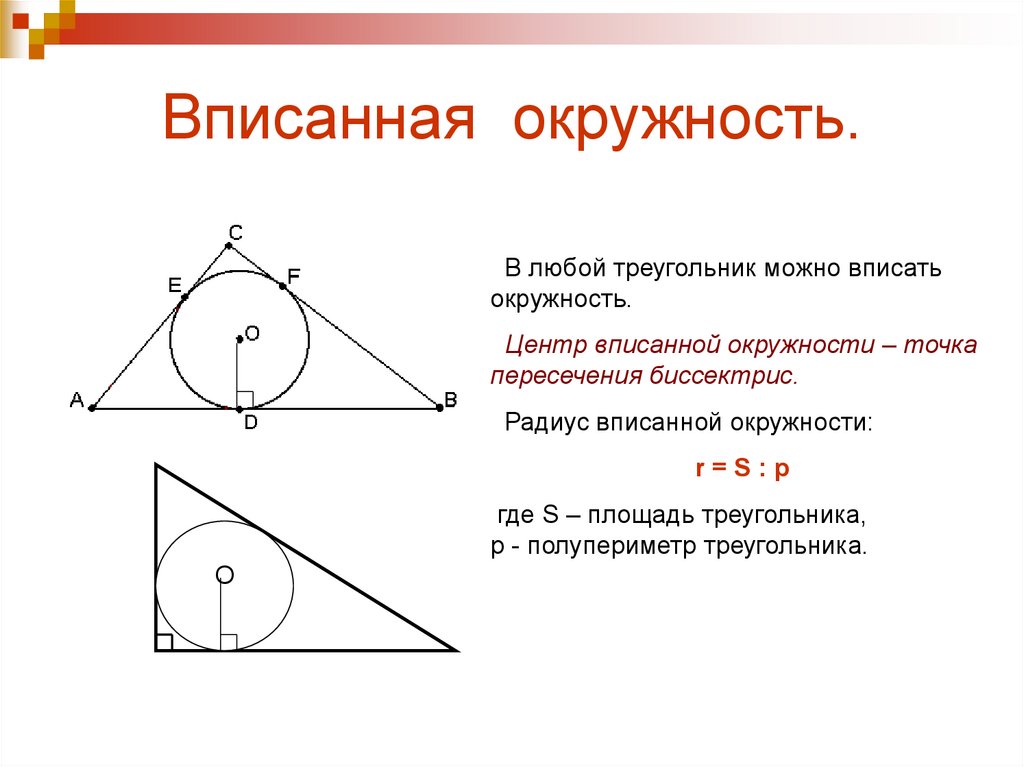
10. Вписанная окружность.
В любой треугольник можно вписатьокружность.
Центр вписанной окружности – точка
пересечения биссектрис.
Радиус вписанной окружности:
r=S:р
где S – площадь треугольника,
р - полупериметр треугольника.
О
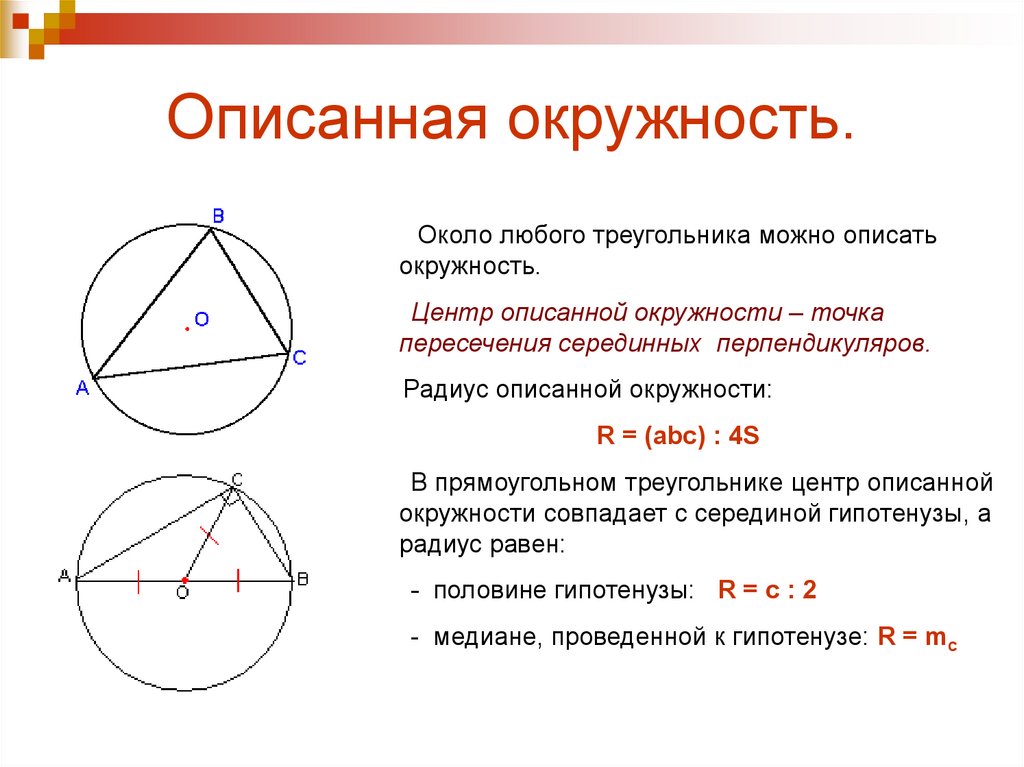
11. Описанная окружность.
Около любого треугольника можно описатьокружность.
Центр описанной окружности – точка
пересечения серединных перпендикуляров.
Радиус описанной окружности:
R = (abc) : 4S
В прямоугольном треугольнике центр описанной
окружности совпадает с серединой гипотенузы, а
радиус равен:
- половине гипотенузы: R = c : 2
- медиане, проведенной к гипотенузе: R = mc
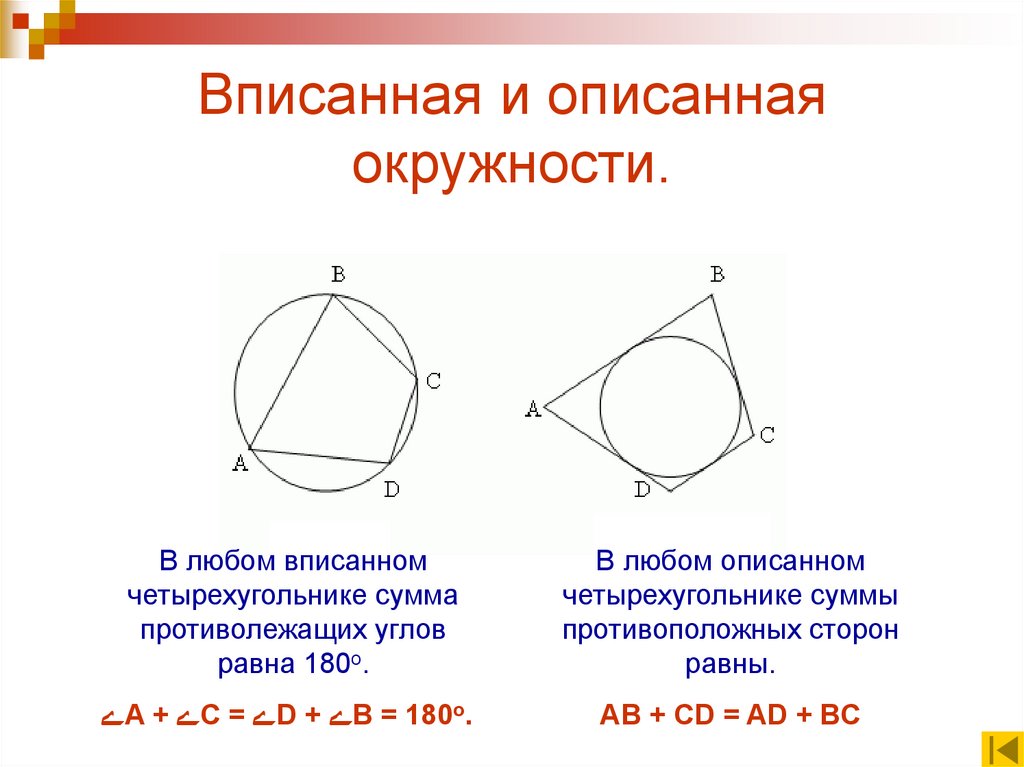
12. Вписанная и описанная окружности.
В любом вписанномчетырехугольнике сумма
противолежащих углов
равна 180о.
В любом описанном
четырехугольнике суммы
противоположных сторон
равны.
ےA + ےC = ےD + ےB = 180о.
АВ + CD = AD + BC
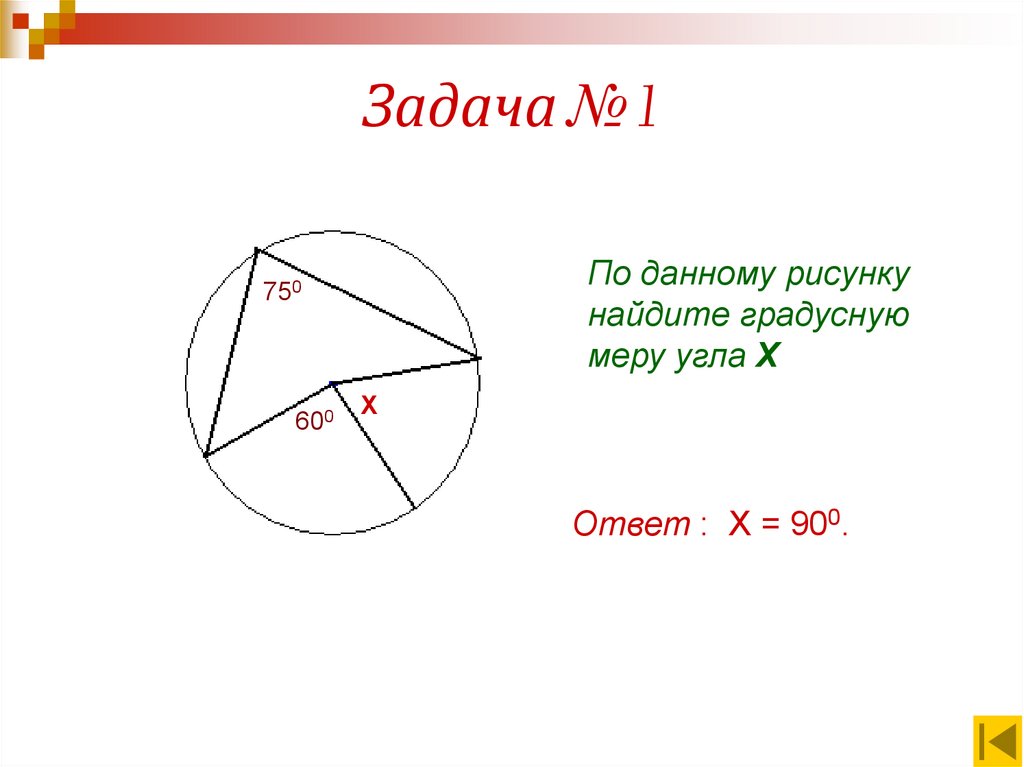
13. Задача № 1
По данному рисункунайдите градусную
меру угла Х
750
600
Х
Ответ : Х = 900.
14.
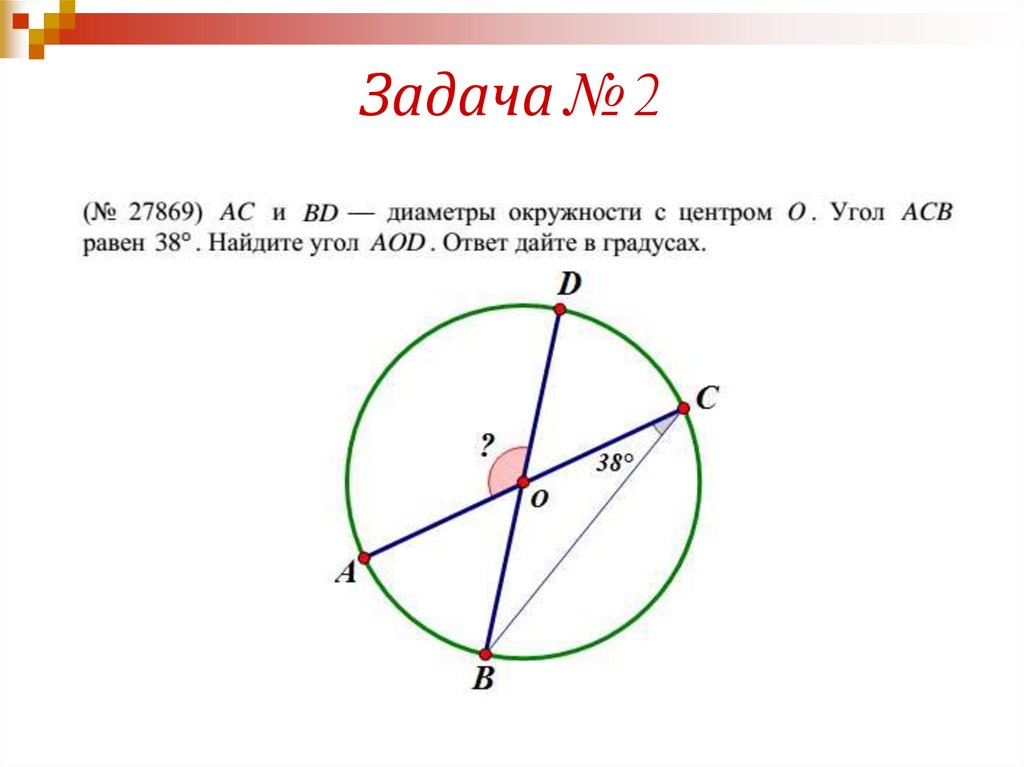
Задача № 215.
Задача № 316.
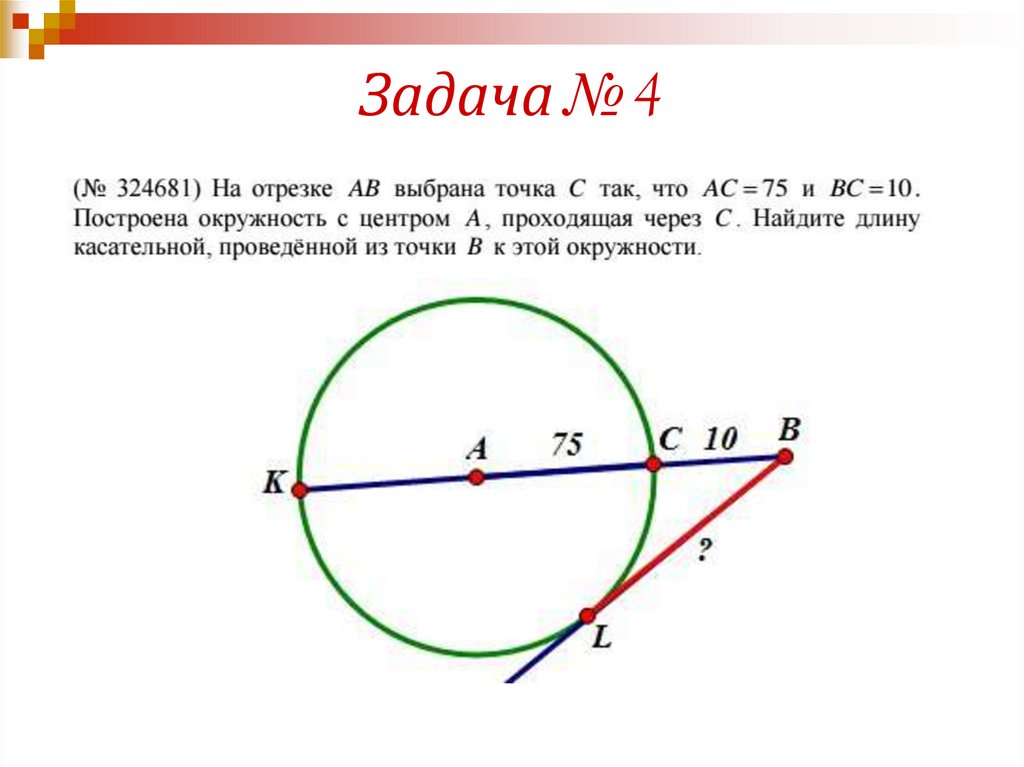
Задача № 417.
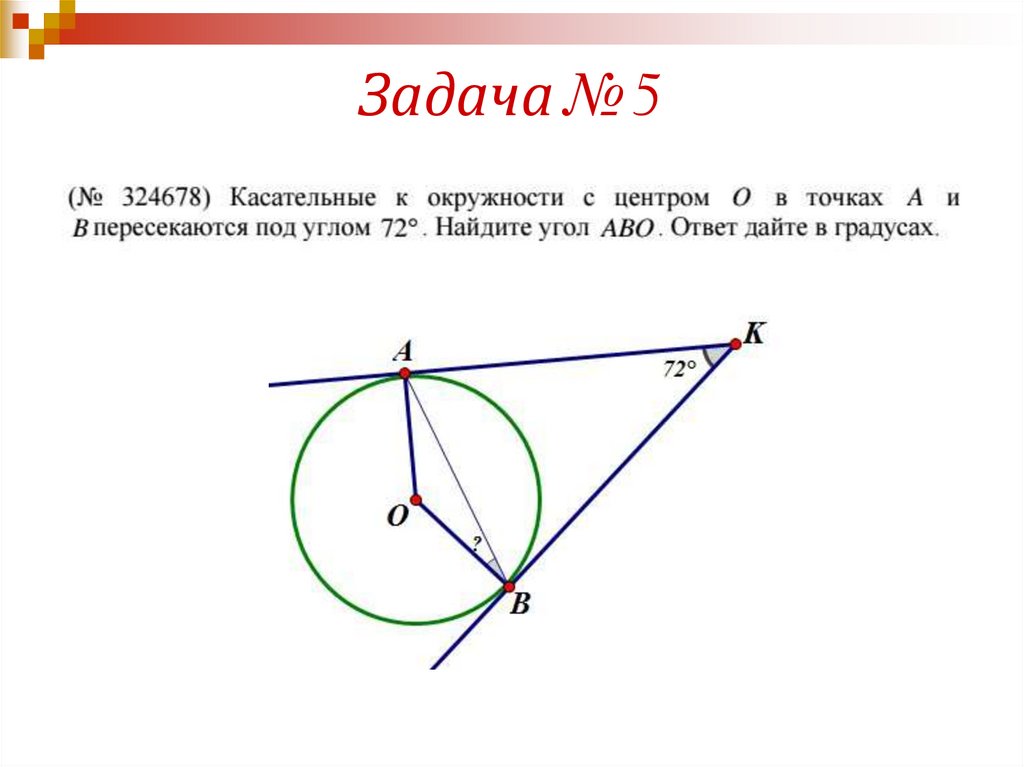
Задача № 518. Задача № 6
ОВ
С
А
Окружность с центром в
точке О касается сторон
угла А (В и С – точки
касания). Отрезок АВ равен
радиусу окружности.
Определите градусную меру
угла А.
Ответ : ےА = 900.






 mathematics
mathematics








