Similar presentations:
Формула перехода от одного основания логарифма к другому
1. Урок-презентация Формула перехода от одного основания логарифма к другому.
Учитель математикиГБОУ СОШ №593 Петрова
Наталья Васильевна
2. Цель:
Вывести формулы перехода от одногооснования логарифма к другому, закрепить
решением задач
3.
I . Проверка д / зII . Устно вычислить
а ) log 1 49;log 5 5;log 12 1;log a a
3
8
б )3
log3 x
2
13
2 log5 2
;5
1 log7 4 log2 7 1 log3 5 log 4 9
;( ) ;2
;4
7
4.
2) Выяснить при каких значениях x существуют логарифмыlog5 (11 x ); log 1 (2 x 1); log0,5 (3x 2 4); log X 1,5; log X ( x 1)
8
3) Решить уравнения :
1
а )log3 x 4; log8 x ; log 1 ( x 1) 2
3
5
1 x 2
2 x 1
б )2 7; 3 ; 4 3; ( ) 1,5
5
3
x
2ч
5.
II. Ход урока.1) Выразить данный логарифм через log с основанием 2
log 4 7; log 1 5; log 2 15; log8 0,1; log 3 5
2
2)Теорема : Пусть x 0, a 0, a , в 0, в 1
log в x
Тогда справедлива формула : log a x
log в a
6.
Доказательство :1) а logв x x прологарифмируем по основанию в
logв а logв x logв x; log а x log в а log в x
logа x
logв x
logв а
2) X 6
log4 x
1
log в а
Например :
log64 2
1
1
log 2 64 6
Применяя эти формулы можно вычислить log числа по любому основанию, используя таблицу
7.
Закрепление.1) Выразить данный логарифм через log с основанием log5 3; log 2 7
2) Вычислить, если lg2 0,301; lg5 0,699
lg2
а )log5 2
lg5
1 log5
б )log 2 5
2 lg2
в )log 2 25 log5 0,5 2log 2 5 log5 2
8.
3) Дано : log3 17 m,найти : log3 51
log3 51 1 m
найти : log27 17
1
log 27 17 m
3
9.
найти : log27 511 1
log 27 51 m
3 3
найти : log9 153
1
log 9 153 1 m
2
10.
4)Упростить :log5 3
81
log6 3
27
log7 3
1
log5 3
9 81
27
1
log6 3
9
1
log 7 3
81log3 5 27log3 6 9log3 7 54 63 7 2 625 216 49 890
11.
5) Решить уравнения :а ) log5 x 2 log5 3 4 log 25 2
log5 x log5 9 4
x 36
б ) log 2 x 2 log 1 x 9
2
log 2 x 2 log 2 x 9
log 2 x 3
x 8
12.
в ) log 22 x 9 log 8 x 4log 22 x 3log 2 x 4 0
log 2 x a
a 2 3a 4 0
a1 4 a2 1
log 2 x 4 log 2 x 1
1
x 16 x
2
13.
Самостоятельная работа :I Вариант
II Вариант
Вычислить :
Вычислить :
1) log 25 35, если log5 7 a
1) log 49 21, если log8 3 a
Решить уравнение :
1
2) log 7 x log 1 x log 49 x
2
7
Решить уравнение :
1
2) log125 x log5 x log 1 x
3
5
14.
Прологарифмировать выражения :2
23
2
3
а ) x 2 log a x log a 2 2 log a 2
3
4
б ) x 0,50,4 0,3
в) x а
1
0,5 а 2
5
log a x log 0,5 log 0, 3
2
1
2
log x 0,5a log a
15.
Произвести потенцирование :log x 3log m 4 log 4
log x log 2 log Sin log Cos
log x log Sin log Cos log Ctg
16.
Д / з.1) Прологарифмировать :
4
x a
3
1
2 3
3 2
a
4
a 3 a 4 a3 a5 8 a7 a6
x
8
a
2) Пропотенцировать :
1) log x log a 2 log в 3log c
2) log x log(1 Sin ) log(1 Sin )
3) log x 2 log( m n ) 3log( m n )









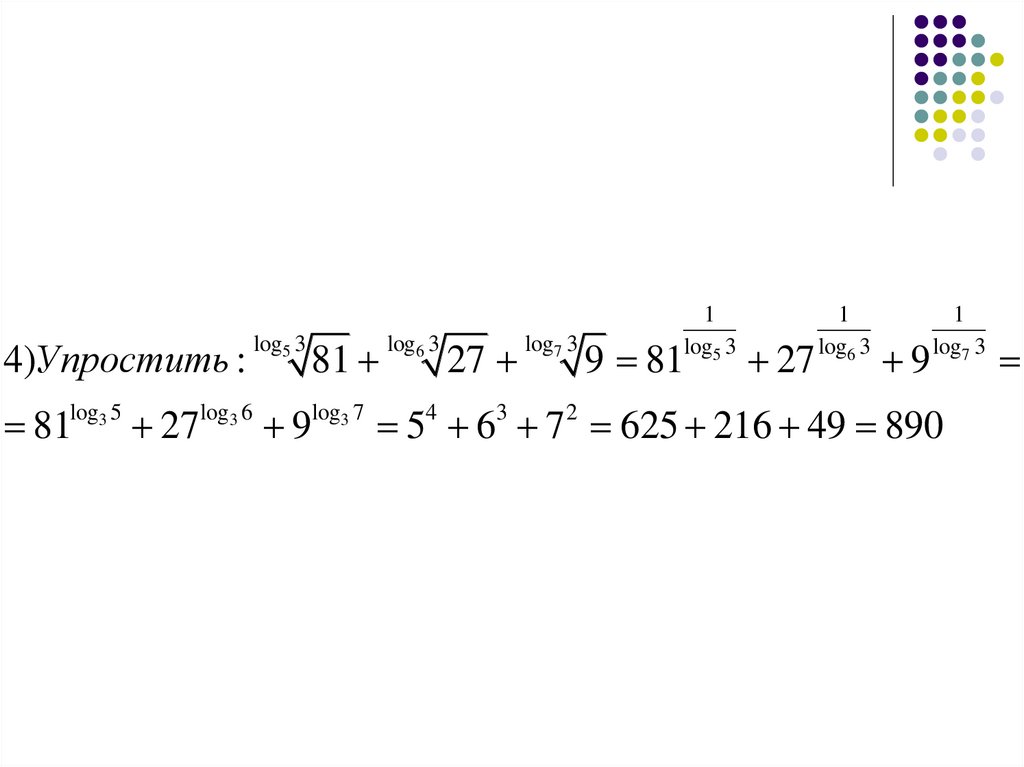

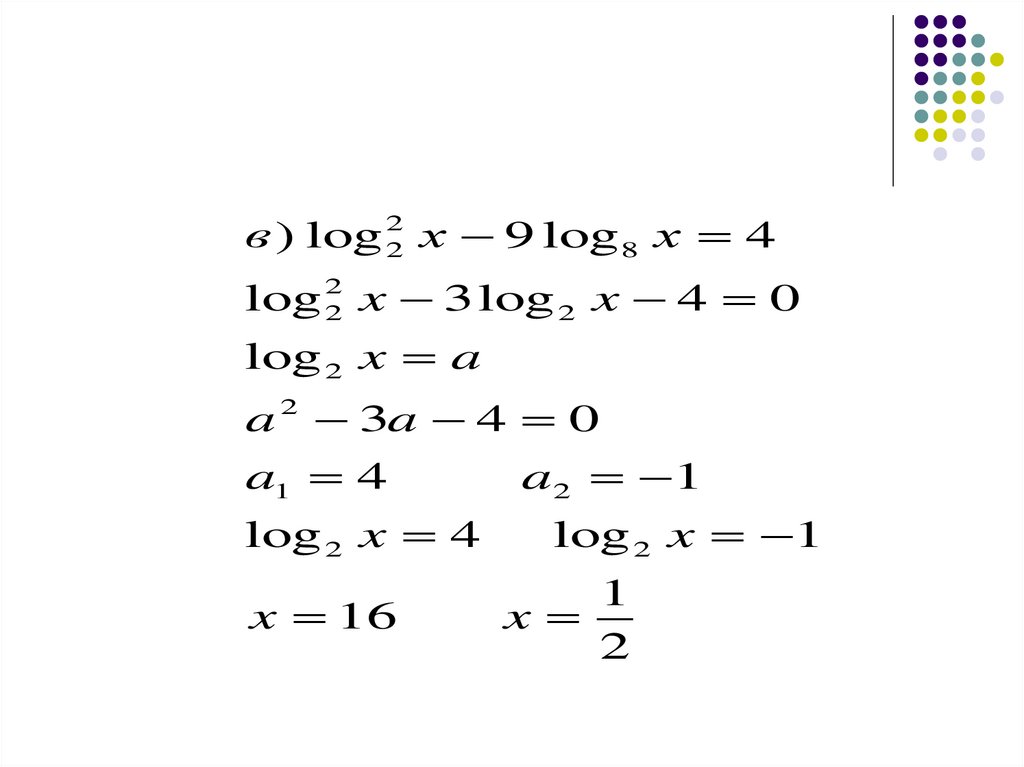



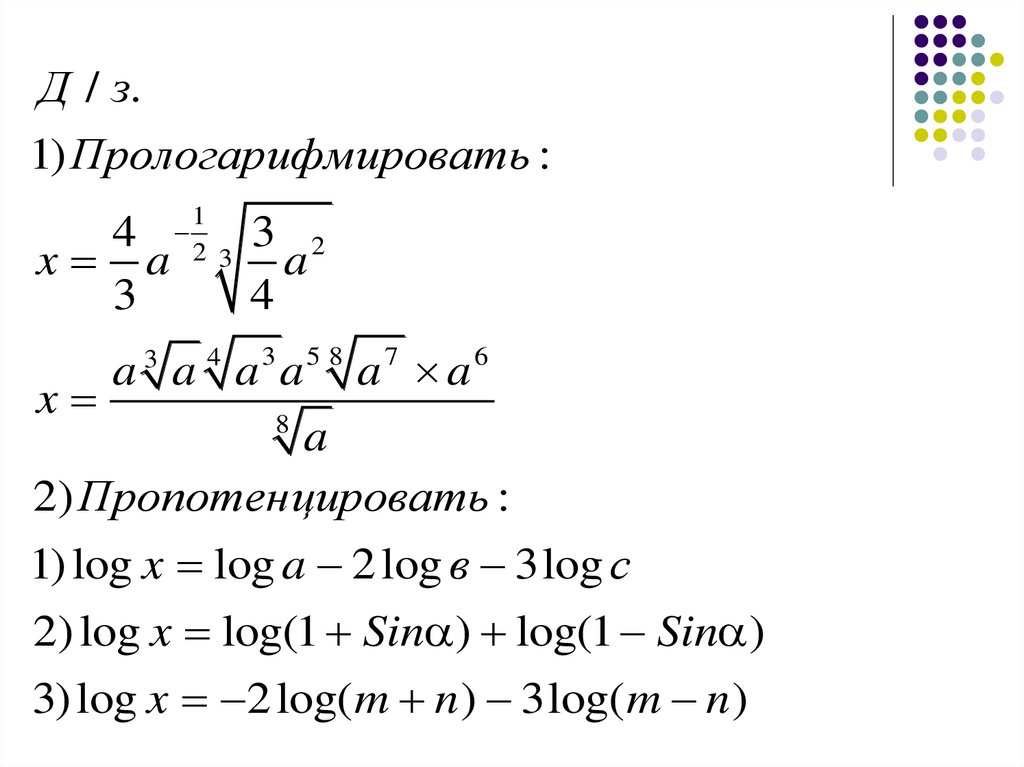
 mathematics
mathematics








