Similar presentations:
Формулы для решения квадратного уравнения
1.
2. Цели урока: проверка усвоение учащимися теории по теме: “Решение квадратных уравнений по формулам”; «открыть» зависимость
Цели урока:проверка усвоение учащимися теории по
теме: “Решение квадратных уравнений по
формулам”;
«открыть» зависимость между корнями
уравнения и его коэффициентами; научить
применять теорему Виета и обратную ей
теорему для решения квадратных
уравнений.
развитие познавательного интереса.
воспитание активной жизненной позиции.
3.
ах вх с 02
D в 4ас
2
в D
х
, если D 0
2а
нет корней , если D 0
4.
ах 2kх с 02
D1 k ас
2
k D1
если D1 0, то х
а
если D1 0, то нет корней
5.
Образец :Уравнение ах вх с 0
2
а ) неполное
б )приведённое
в ) полное
6.
7.
Теорема ВиетаСумма корней приведённого
квадратного уравнения равна
второму коэффициенту, взятому с
противоположным знаком, а
произведение корней равно
свободному члену.
8.
Доказательство:рассмотрим приведённое квадратное уравнение
х рх с 0
2
Пусть D 0 и D р 4ас
2
Тогда это уравнение
имеет два корня :
р D
х1
2
и
р D
х2
2
9.
Найдём сумму и произведение корнейр D р D 2р
х1 х2
р
2
2
2
2
2
р D р D ( р) ( D )
х1 х2
2
2
4
2
2
р ( р 4q ) 4q
q.
4
4
10.
Итак:х1 х2 р
х1 х2 q
11.
Пример 1: Найдём сумму и произведениекорней уравнения
3х 2 5 х 2 0
D 25 4 3 2 1 0
Сделаем приведённое
квадратное уравнение
5
2
х х 0
3
3
5
х1 х2
3
2
х1 х2
3
2
12.
Обратная теорема:Если числа х1 и х2 таковы,
что их сумма равна р,
а произведен ие равно q,
то эти числа являются
корнями уравнения
х рх q 0
2
13.
Пример: Найдём подбором корни уравнениях х 12 0
2
Пусть х1 и х2 корни уравнения
Тогда х1 х2 1
х1 х2 12
Нетрудно догадаться ,
что х1 3 х2 4
14.
По праву достойна в стихах быть воспетаО свойствах корней теорема Виета.
Что лучше, скажи постоянства такого:
Умножишь ты корни – и дробь уж готова.
В числителе с, в знаменателе а.
А сумма корней также дроби равна.
Хоть с минусом дробь, что за беда!
В числителе в, в знаменателе а.
ах 2 вх с 0
х1 х2
с
а
х1 х2
в
а
15.
Домашнее задание:выучить теоремы и решить № 575(а,в,д)
№ 577


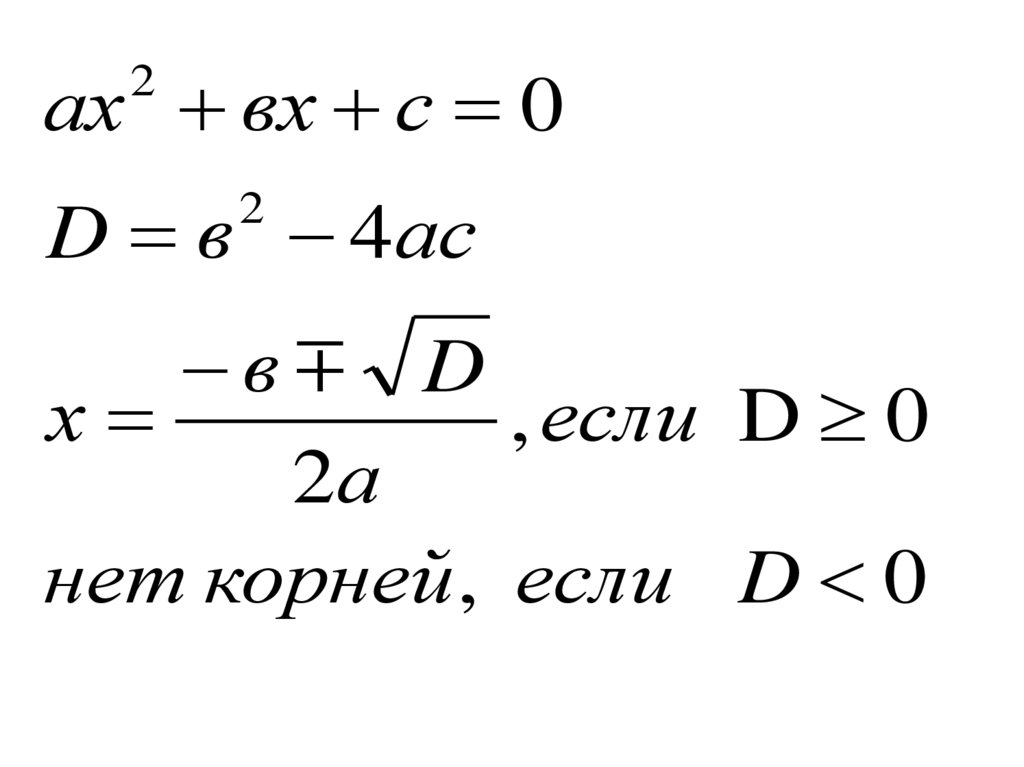
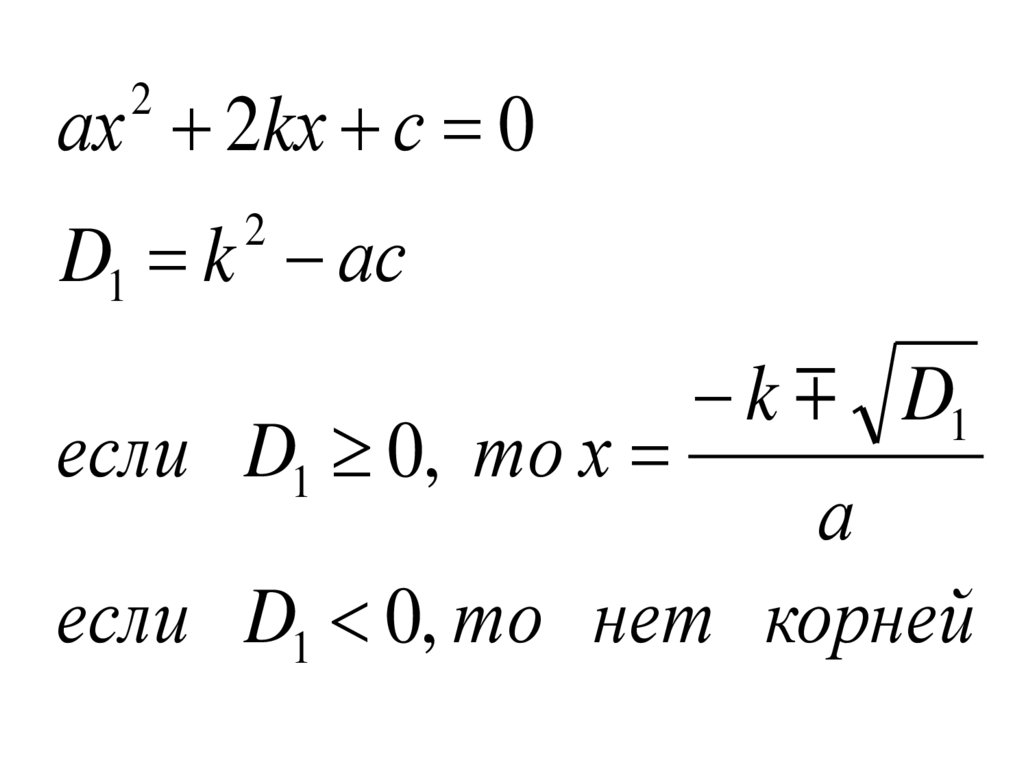
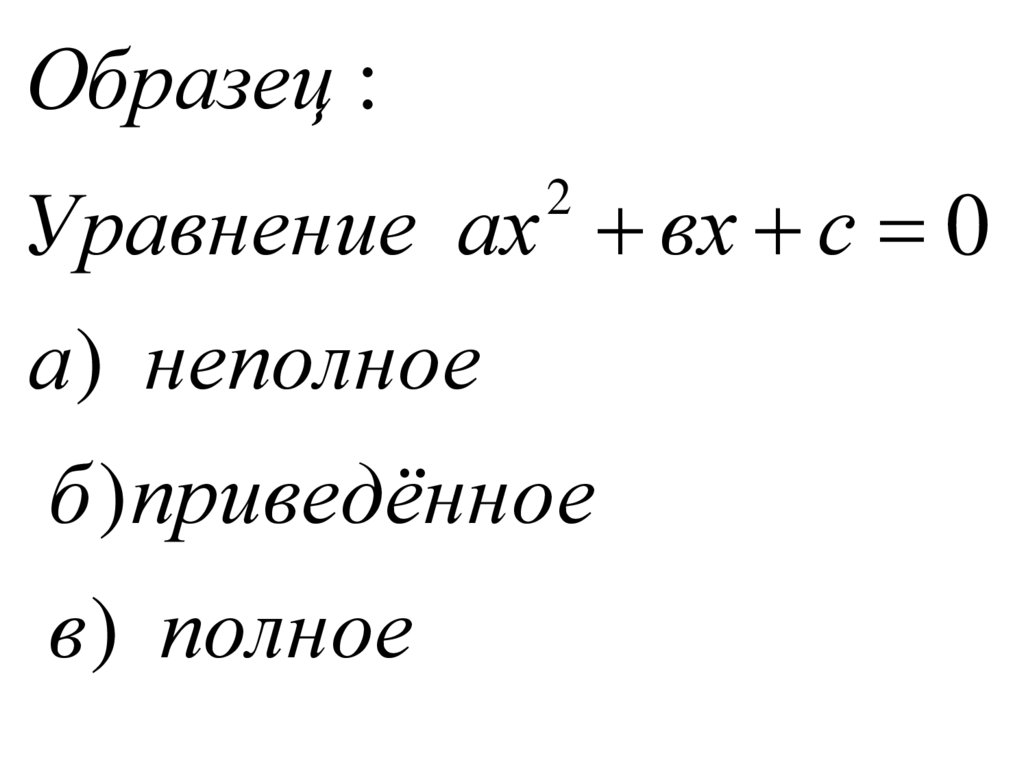




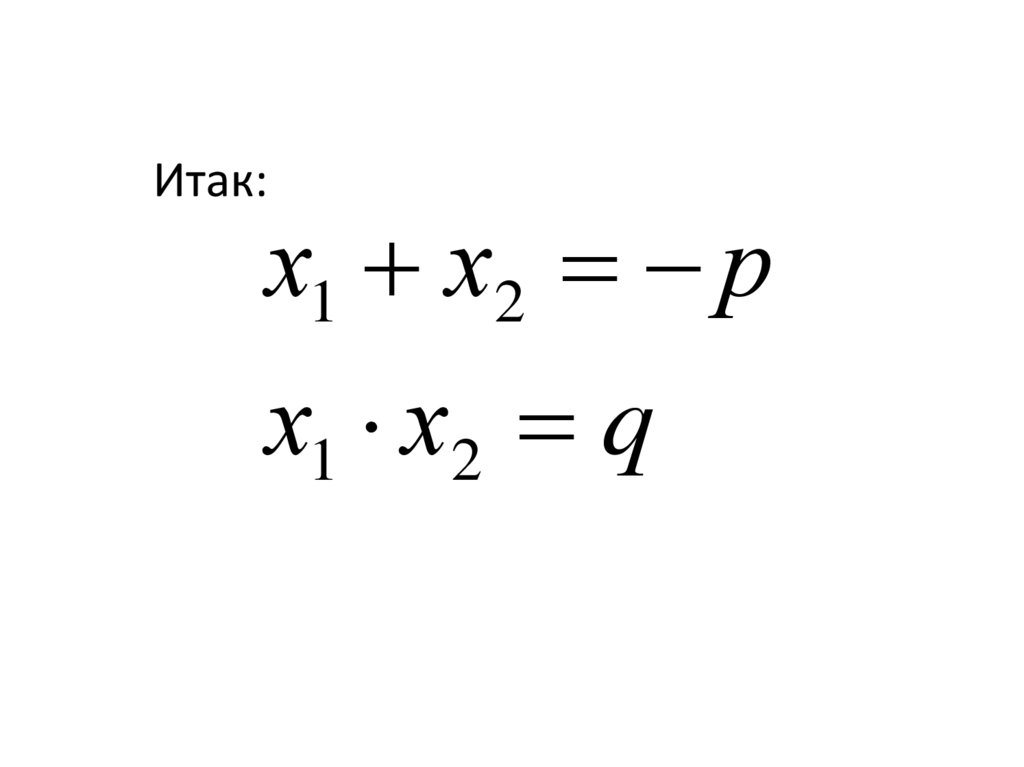





 mathematics
mathematics








