Similar presentations:
Касательная. Уравнение касательной
1.
ТЕМА УРОКА:«Касательная.
Уравнение касательной»
2. Девиз урока:
Плохих идей не бываетМыслите творчески
Рискуйте
Не критикуйте
3.
Используя формулы и правила дифференцирования,найдите производные следующих функций:
1. у 2 х10
у 20х 9
2. у 4 х
у
3. у 7 х 4
у 7
5
4. у tgx
x
у
5. у х 3 sin x
у 3х 2 sin x x 3 cos x
х
6. у
3 4х
2
2
х
1
5
cos 2 x x 2
у
6х 4х 2
3 4 х 2
4. Согласны ли вы с утверждением:
Касательная – это прямая,имеющая с данной кривой
одну общую точку
5.
yy = 2х - 1
y = x2
1
y
x
х =1
y = cos x
-π
π
x
y = -1
х =π
6.
7.
yy = 2х - 1
y = x2
1
x
х =1
Касательная – предельное
положение секущей
8.
y=kx+bk- угловой коэффициент
k = tgα
f´(x) = tgα
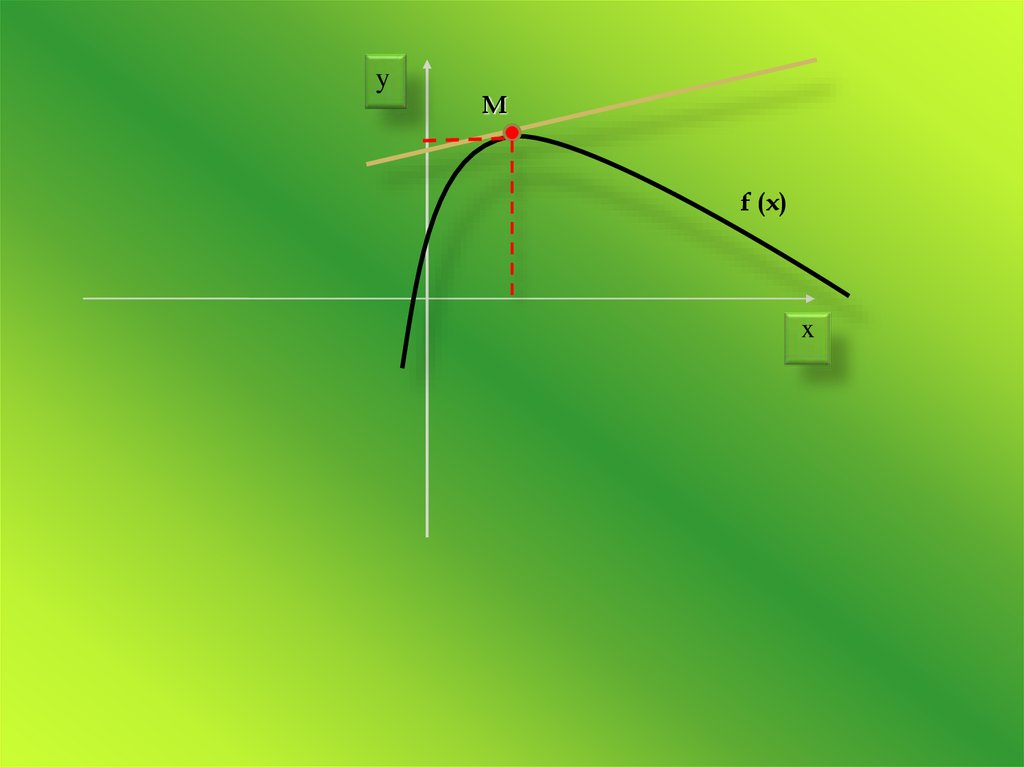
9.
yM
f (x)
x
10. Уравнение касательной
y = f(a) + f / (a) · (x - a)(a;f(a)) – координаты точки касания
f´(a) = tgα =k – тангенс угла наклона
касательной в данной точке или угловой
коэффициент
(х;у) – координаты любой точки
касательной
11. Алгоритм
1. Обозначим абсциссу точки касаниябуквой а
2. Вычислим f(а)
3. Найдем f´(x) и вычислим f´(а)
4. Подставим найденные значения в общее
уравнение касательной.
5. y = f(a) + f / (a) · (x - a)
12.
Сf(x)=√(3-2x)
f'(1)=?
Я
f(x)=5/³√(3x+2)
f' (-1/3)=?
Ю
f(x)=12/√(3x²+1)
f' (1)=?
Ф
f(x)= 4√(3-2x²)
f' (-1)=?
К
f(x)=2ctg2x
f' (-π/4)=?
И
f(x)=4/(2-cos3x)
f' (- π /6)=?
Л
f(x)= tg x
f' (π /6)=?
1
4/3
9
-4
Ф л ю к
-1
-3
5
с и я
13.
14. Потренируемся:
Составить уравнениекасательной к графику
функции f(x)=x²-3x+5 в
точке с абсциссой а = -1
15. Задания ЕГЭ 2011 В-8
Функция у = f(x)определена на
промежутке (-3; 4).
На рисунке
изображён её график
и касательная к
этому графику в
точке с абсциссой
а = 1. Вычислите
значение
производной f'(x) в
точке а= 1.
16.
Функция у = f(x)определена на
промежутке (-3;4). На
рисунке изображён её
график и
касательная к этому
графику в точке с
абсциссой а = -2.
Вычислите значение
производной f'(x) в
точке а = -2.
17. Домашнее задание
Подготовка к ЕГЭВ-8
№ 3 - 10
18. Самостоятельная работа Напишите уравнение касательной к графику функции у=f(x) в точке с абсциссой а. вариант 1 вариант 2
f(x) = х²+ х+1, а=1f(x)= х-3х², а=2
19.
20. Подведение итогов
Что называется касательной к графикуфункции в точке?
В чём заключается геометрический смысл
производной?
Сформулируйте алгоритм нахождения
уравнения касательной в точке?
21.
Выберете смайлик, соответствующий вашемунастроению и состоянию после проведенного урока
тревожно, не уверен в себе
спокойно, у меня все получится
безразлично, что будет, то и будет





















 mathematics
mathematics








