Падение плоской ЭМВ на границу раздела двух сред

1. Электромагнитные поля и волны Практическое занятие №2

ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ И
ВОЛНЫ
Практическое занятие №2
ПАДЕНИЕ ПЛОСКОЙ ЭМВ НА ГРАНИЦУ
РАЗДЕЛА ДВУХ СРЕД

2.

• Основные расчетные формулы:
1. Первый и второй законы Снеллиуса
(2.1)
3 1 ,
sin 2 N1
(2.2)
,
sin 1 N 2
• где 1, 2 , 3
- углы падения, преломления и
отражения соответственно; N1 и N 2 - показатели
преломления сред.
2. Коэффициенты Френеля для волн вертикальной
поляризации
N 2 cos 1 N1 cos 2
2 N1 cos 1
R
;
T
. (2.3)
||
||
N 2 cos 1 N1 cos 2
N 2 cos 1 N1 cos 2
• и для волн горизонтальной поляризации
R
N1 cos 1 N 2 cos 2
;
N1 cos 1 N 2 cos 2
T
2 N1 cos 1
.
N1 cos 1 N 2 cos 2
(2.4)

3.

• 3. Угол Брюстера определяется из равенства
N
. (2.5)
0 arctg 2
N1
4. Критический угол
N2
кр arcsin
. (2.6)
N1
5. Граничные условия на поверхности реального
проводника (граничные условия Леонтовича-Щукина)
(2.7)
E2 n Z2 n H1 n,
• где - вектор нормали к поверхности проводника.
• Эти же условия в скалярном выражении
E
Z
H
(2.8)
1
2 1 .

4.

• 1. Под каким углом должна падать плоская волна из
воздуха 0 , 0 на границу раздела со стеклом
• 8 , , чтобы не было отражения.
a2
0 a2
0
• Решение:
• По условию задачи имеет место полное преломление,
поэтому рассматриваемый случай относится к случаю
падения вертикально поляризованной волны под
углом падения, равным углу Брюстера при N1 N2 a .a
• Коэффициент Френеля для отраженной волны (при
вертикальной поляризации) можно найти по
выражению:
1
N 2 cos 1 N1 cos 2
R ||
,
N 2 cos 1 N1 cos 2
2

5.

• N1 1 1, N2 2 8
где .
• Отражение отсутствует при R || 0 , что
соответствует 1 0 - углу Брюстера.
Поэтому можем записать, что N 2 cos 0 N1 cos 2 0,
N 2 cos 2
тогда получим:
N1 cos 0
N 2 sin 0
• Из второго закона Снеллиуса N1 sin 2
• Следовательно, sin 0 cos 2
sin 2 cos 0
• Это равенство справедливо только в случае,
если sin 0 cos 2 и sin 2 cos 0
N 2 cos 0 N1 cos 2 N 2 cos 0 N1 sin 0 0
• Таким образом
N2
tg 0
8 2,83
N1

6.

• отсюда можем найти
• 0 arctg (2,83) 70,54 , 2 arccos sin( 0 ) 19,46
.

7.

• 2. Плоская электромагнитная волна падает по нормали
из воздуха на пластину диэлектрика радиопрозрачного
укрытия станции ближней навигации без потерь
толщиной d. Определить условия, при которых пластина
становится прозрачной для падающей волны.
Показатель преломления диэлектрика N2.
• Решение:
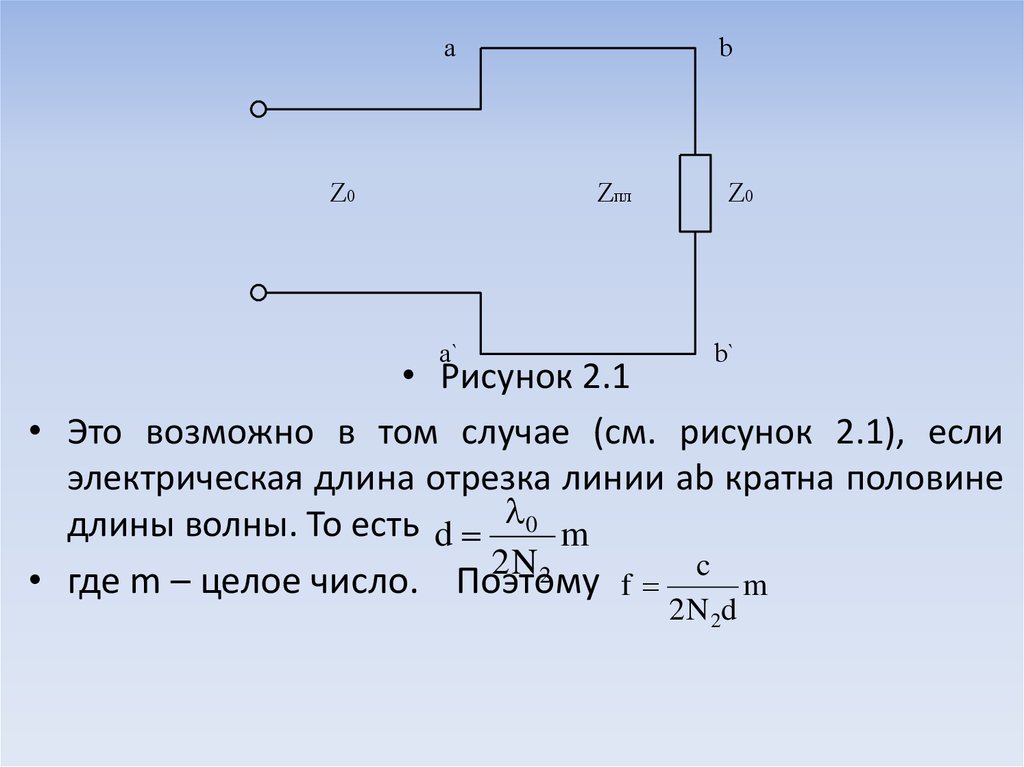
Эквивалентная схема решения задачи изображена
на рисунке 2.1. Отражение от сечения aa не будет в
случае, если входное сопротивление линии в этом
сечении равно Z0.

8.

a
Z0
b
Zпл
a`
Z0
b`
• Рисунок 2.1
• Это возможно в том случае (см. рисунок 2.1), если
электрическая длина отрезка линии ab кратна половине
длины волны. То есть d 0 m
2N2
• где m – целое число. Поэтому f c m
2 N 2d

9.

• 3. Плоская электромагнитная волна падает нормально
из воздуха на поверхность морской воды ( a 2 81 0 ).
Вычислить, сколько процентов падающей мощности
отразится от поверхности, а сколько пройдет в воду.
• Решение:
2 поверхности
Мощность волны, падающей
на
1
м
E 2m
СР
раздела
,
2 Z1
• где E m-1 амплитуда напряженности поля падающей
волны, Z1 – волновое сопротивление воздуха.
2 поверхности
Мощность волны,
отраженной
от
1
м
2
E
раздела СР m3
ОТР
2 Z1
E
• где m3 - амплитуда напряженности поля отраженной
волны. Поэтому СРОТР R||2
1
ПАД
СРПАД

10.

• есть квадрат коэффициента Френеля.
• Мощность волны, прошедшей
в воду через 1м2
2
E m2
поверхности CРПРЕП
2 Z2
E
• где m2- амплитуда напряженности поля преломленной
волны, Z2 – волновое сопротивление воды. Поэтому
CРПРЕЛ
CР ПАД
Z1 2
T||
Z2
• где
- квадрат коэффициента преломления Френеля.
2
T||
Поскольку
по условию, то 1 2 3 0
2
Z Z2
R ||2 1
Z1 Z2
2
2
Z1
377
Z
377
1
9
9
0,64 64%
Z
377
Z 1 377
1
9
9
Z1
377
4 377
9
9 0,36 36 %
T||2
2
2
Z1
377
Z1
377
9
9
4Z1
• - есть ответ на вопрос задачи.

11.

• 4. Плоская линейно поляризованная волна падает
нормально на идеально проводящую пластину. Найти
поле отраженной волны и суммарное поле.
Решение:
Примем, что идеально проводящая пластина лежит
в плоскости декартовой системы координат. Для
i t kz
падающей волны. E пад E1ei t kz ;
H
H
e
пад
1
i t kz
• Для отраженной волны: E отр F E1ei t kz ;
H
отр FH1e
• Найдем величину E отр и направление . Для этого
случая коэффициент Френеля можно определить:
R
Z2 Z1
Z2 Z1
• где Z1 и Z2 – волновые сопротивления первой и второй
среды соответственно. Полагая, что 2 , получим

12.

0
Z2
0
• поэтому F = - 1, откуда следует, что E3 E1, H1 H3 из
граничных условий на поверхности идеального проводника.
i t kz
Из этого следует: E отр Е1еi t kz ;
H
H
е
отр
1
• Суммарное поле в среде над поверхностью идеального
проводника может быть найдено:
E E ПАД Е ОТР 2iE1ei t sin kz;
H
H
Н
2Н еi t cos kz.
ПАД
ОТР
1
• Оно представляет собой стоячую волну. Узлы и пучности
электрического и магнитного полей сдвинуты по оси z на λ
, а во времени поля сдвинуты на четверть
π периода (об
этом свидетельствует множитель i ei 2 в формуле для
напряженности электрического поля).
4

13.

• 5.
Эллиптически
поляризованная
волна
с
коэффициентом эллиптичности к э 0,4 и вращением
1
вектора E по часовой стрелке падает из воздуха на
поверхность S диэлектрика ( 4,5) так, что большая ось
эллипса поляризации лежит в плоскости падения. Каким
должен быть θ1
, чтобы отраженная волна была
линейно
поляризована?
Найти
коэффициент
эллиптичности преломленной волны.
Решение
Падающая эллиптически поляризованная волна
может быть представлена в виде суммы двух линейно
поляризованных волн: вертикально и горизонтально
поляризованных (
) , представленных на
E1|| и E1
рисунке 2.2.

14.

Плоскость
падения
E1||
E1
E3
n
1 3
E ||2
2
S
E 2
Рисунок 2.2.

15.

• Если 1 будет равен углу Брюстера, то вертикально
поляризованная часть волны ( E1|| ) полностью перейдет
во вторую среду.
• При этом tg 1 2 1 4,5 2,12; 0 1 arctg(2,12) 64,76o.
• Отражение будет испытывать лишь горизонтально
поляризованная составляющая волны. Тогда
E 2 E1 T ;
E||2
E1|| T|| ;
T
2 N1 cos 1
;
N1 cos 1 N 2 cos 2
2 N1 cos 1
T||
.
N 2 cos 1 N1 cos 2
• Соотношения фаз между E1|| и E1 во второй среде не
изменится, следовательно, поляризация волны во
второй среде будет той же, как и в первой, то есть
эллиптической.

16.

• Коэффициент эллиптичности во второй среде
E 2 E1 T
T
к э2 || ||
к э1
T||
E2
E1 T||
• то есть к э 2 к э1 N 2 cos 1 N1 cos 2
N1 cos 1 N 2 cos 2
• Так как известно, что при полном преломлении
• 0 2 90o , получим, что 2 90o 56,3o 25,24o.
• Далее, cos 0 cos 64,76 0,43 ; cos 2 cos 25,24 0,9
, N1 1 ,
• Тогда можем определить искомый коэффициент
эллиптичности (при этом учтем, что коэффициент
преломления второй среды ): N 2 a a 2,25 1,5
2
к э 2 0,4
2,12 0,43 0,9
0,31
0,43 2,12 0,9
1

17.

• Контрольные вопросы:
1. Сформулируйте законы Снеллиуса.
2. Что показывают коэффициенты Френеля?
3. Дайте определение показателя преломления
среды.
4. Поясните сущность эффекта полного
преломления. Каковы условия проявления этого
эффекта?
5. Поясните сущность эффекта полного внутреннего
отражения. Каковы условия проявления этого эффекта?
6. Что такое поверхностная волна? От чего зависит
фазовая скорость ее распространения?
7. Сформулируйте граничные условия ЛеонтовичаЩукина. В чем их физическая сущность и каково
практическое значение?
8. Почему граничные условия Леонтовича-Щукина
следует считать приближенными?