Similar presentations:
Оптика. Матричная теория Гауссовой оптики. (Лекция 6)
1. Оптика.
Лекция 6.Матричная теория Гауссовой оптики
2. Преобразование координат лучей оптической системой
Основное действие оптической системы заключается в изменении хода лучей, котороеописывается преобразованиями двух параметров – линейной и угловой координат
луча. Эти преобразования наиболее удобно описывать при помощи
аппарата матричной оптики. Матрица преобразованияполностью описывает
распространение лучей через оптическую систему.
Параметры луча в пространстве
предметов и изображений могут быть
заданы только в том случае, если
выбраны опорные плоскости. Опорная
плоскость (ОП) – это некоторая
произвольно выбранная плоскость,
перпендикулярная оптической оси.
Опорные плоскости в пространстве
предметов и изображений выбираются
из соображений удобства и могут быть
либо сопряженными, либо нет.
Вместо угла α часто используют направляющий косинус оптического лучевого вектора:
Y n cos y n sin n
3.
yY
(ОС)
y
Y
y a0 a1 y a2Y a3 y 2 a4 yY a5Y 2 ...
Y b0 b1 y b2Y b3 y 2 b4 yY b5Y 2 ...
Если оптическая система является центрированной, то a0=b0=0. Все члены ряда,
начиная с a3 и b3, можно отбросить, так как они стремятся к нулю на порядок
быстрее, чем предыдущие. Таким образом, для идеальной оптической системы:
y Ay BY
Y Cy DY
4. Матрица преобразования лучей
y A B yY C D Y
Все свойства идеальной оптической системы полностью описываются матрицей
преобразования лучей , называемой также гауссовой матрицей или ABCD-матрицей
A B
G
C D
5. Геометрический смысл элементов матрицы преобразования
Рассмотрим луч с координатами , y=1, Y=0y Ay BY A
Y Cy DY C
y
f
y
S F
C учетом того, что , y=1 можно получить
S
y S F F
f
Y n
S F
f
n
C
f
A
n
f
6. Геометрический смысл элементов матрицы преобразования
Рассмотрим луч с координатами , Y=1 (α=-1/n), Y’=0 (α’=0)y Ay BY Ay B
Y Cy DY Cy D 0
f
y f
n
S
y S F F
n
C учетом того, что , y=1 можно получить
S
y S F F
f
n
f
n S F n S F S F
D Cy
f
n
f
n
f
f S S S S
f S S f f
B y Ay F F F F F F
n f n
n f
n
n f
Y n
7. Геометрический смысл элементов матрицы преобразования
S Ff
G
n
f
S F S F f f
n f
SF
f
Элемент матрицы С зависит только от
параметров оптической системы, а
элементы A,B, D и зависят еще и от
выбора опорных плоскостей.
Определитель матрицы преобразования
det G AD BC 1
8. Обратная матрица преобразования
G -1G GG 1 I1 0 - единичная матрица
I
0
1
Обратная матрица преобразования описывает обратное преобразование (из выходных
координат во входные)
b G 1 b
D B
1
G
C
A
Условие сопряжения опорных плоскостей
В общем случае все элементы матрицы преобразования не равны нулю, но для
случая сопряженных опорных плоскостей элемент B=0. Для сопряженных опорных
плоскостей элемент A имеет значение линейного увеличения, а элемент D - величина
обратная элементу A.
9. Виды матриц преобразования
Матрица преломленияСуществуют два основных вида матриц
преобразования, описывающих два простых
преобразования – перенос луча в свободном
пространстве и преломление луча на
преломляющей поверхности или в оптической
системе.
Для вывода матрицы преломления
совместим опорные плоскости с главными
плоскостями
Поскольку опорные плоскости сопряжены,
то B=0 и y’=Ay. Тогда A=1, а поскольку
определитель матрицы всегда равен
единице , следовательно D=1.
0
1
R
1
- матрица преломления
10. Виды матриц преобразования
Матрица переносаПри переносе луча изменяется только линейная
координата.
Y
y y d y d
n
Угловая координата не изменяется
Y Y
d
1
T
n - матрица переноса
0
1
d
- приведенное расстояние между опорными плоскостями
n
11. Матрица одной преломляющей поверхности
Изтреугольников OKC и CKO’
можно вывести
Домножим оба выражения
на n и n’ соответственно
n n n
n n n
Из закона преломления следует, что
n n
n n n n
y
Y Y n n
r
y
r
Y Y y n n
0
1
R
n n 1
12. Матрица зеркальной (отражающей) поверхности
n n0
1
R
2 n 1
Для плоского зеркала
1 0
R
0 1
Следовательно, плоское зеркало не меняет хода луча (геометрический косинус
изменяется, а оптический преломленный (отраженный) косинус остается прежним).
13. Матрицы оптической системы, состоящей из нескольких компонентов
Любую оптическую систему можно представить как совокупность несколькихкомпонентов, разделенных промежутками. Пусть дана некоторая произвольная
система, в которой для каждого компонента известно положение главных
плоскостей и оптическая сила, а также известны расстояния между компонентами
и показатели преломления
G T3 R3T2 R2T1T0 Tn Rn ...T1R1T0
1
Rn
1
0
, Tn
1
dn
nn
1
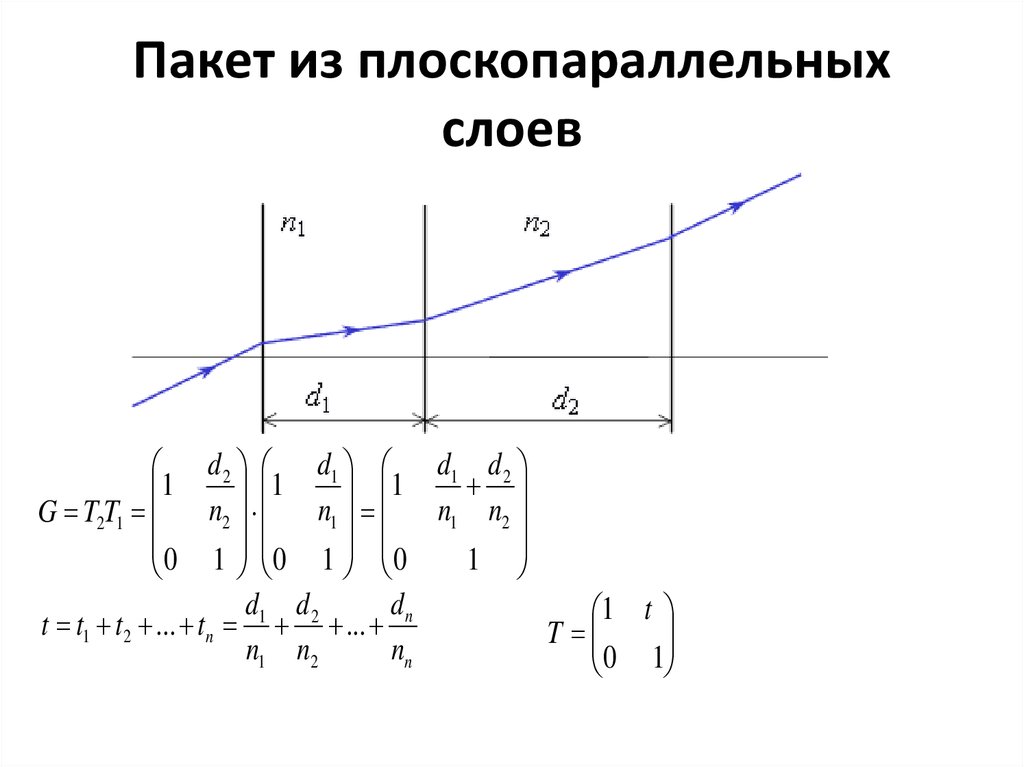
14. Пакет из плоскопараллельных слоев
d 2 d1 d1 d 21
1
1
G T2T1 n2 n1 n1 n2
0 1 0 1 0
1
dn
d1 d 2
1 t
t t1 t2 ... tn ...
T
n1 n2
nn
0 1
15. Оптическая система с нулевыми расстояниями между компонентами
0 10 1
1
G R2 R1
2 1 1 1 1 2
0
1
то есть оптические силы таких компонент складываются
1 2 ... n
16. Двухкомпонентная оптическая система
G R2 DR11 2 1 2
d
n
Рассмотрим частные случаи двухкомпонентной системы.
Если d=0, тогда Ф=Ф1+Ф2.
Если t=d/n=1/Ф1, это значит, что второй компонент (его главная плоскость) находится
в заднем фокусе первого компонента. Тогда Ф=Ф1, то есть второй компонент может
иметь какую угодно оптическую силу.
Если t=d/n=1/Ф1, то первый компонент находится в переднем фокусе второго
компонента, тогда Ф=Ф2.
d 1 2 1 1
Если t
n 1 2 1 2
то
0
17. Афокальные (телескопические) системы
Афокальные или телескопические системы – это системы из двух или болеекомпонентов, оптическая сила которых равна нулю. Такие системы предназначены для
наблюдения удаленных объектов.
У афокальных систем оптическая сила равна нулю, то есть C=-Ф=0, следовательно,
определитель матрицы detG=AD-BC. Отсюда D=A-1. Тогда матрица будет выглядеть
следующим образом:
A B
G
1
0 A
Если опорные плоскости сопряжены, то B=0 , и следовательно:
A 0
G
1
0 A
y Ay BY Ay
Y Cy DY A 1Y
Для афокальной системы элемент матрицы равен линейному (поперечному)
увеличению, а его обратная величина имеет смысл углового увеличения:
18.
В телескопических системах линейное и угловое увеличение не зависят от положениясопряженных опорных плоскостей и, следовательно, не зависят от положения
предмета и изображения:
y
const A
y
Y
const A 1
Y
t
Двухкомпонентная оптическая система телескопическая,
если задний фокус первого компонента совпадает
с передним фокусом второго
d 1 2 1 1
n 1 2 1 2
Линейное увеличение такой системы:
y f 2
y f1
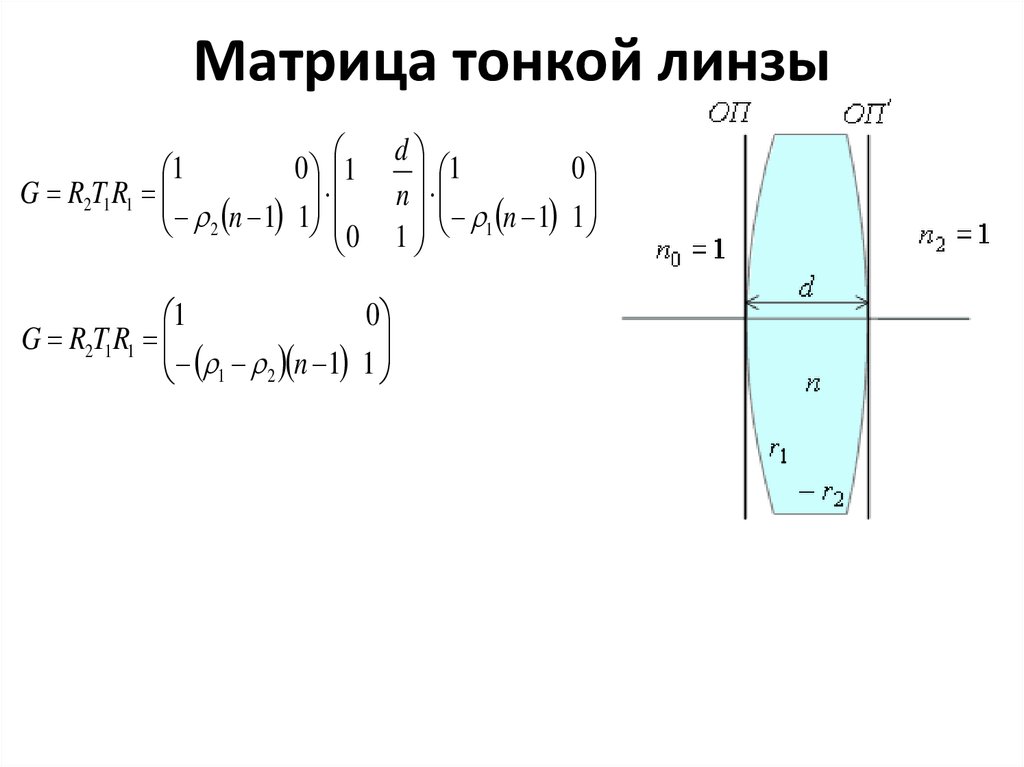
19. Матрица тонкой линзы
1G R2T1 R1
2 n 1
0 1
1
0
1
G R2T1R1
1 2 n 1
d
1
n
n 1
1 1
0
1
0
1
20. Расчет параксиальных (нулевых) лучей через оптическую систему
Нулевые лучи – это лучи, которые преломляются по законам параксиальной оптики, ноимеют произвольно большие координаты.
Расчет нулевых лучей через оптическую систему состоит из операций переноса луча
между компонентами и преломления луча на компонентах, которые можно описывать
либо в матричной форме, либо в виде рекуррентных соотношений:
d
y y Y
n
Y Y y
Вычисления выполняются столько раз, сколько компонентов имеется в оптической
системе. Однако, для полного расчета лучей через оптическую систему вначале
нужно определить координаты лучей в пространстве предметов, а после завершения
расчетов определить координаты лучей в пространстве изображений. Таким
образом, расчет нулевых (параксиальных) лучей включает в себя три этапа:
определение входных координат луча,
вычисление хода луча (последовательное определение его координат на всех
компонентах),
определение выходных координат луча.



















 physics
physics








