Similar presentations:
Графовые модели программы. Алгоритм оптимизации информационного графа по ширине пи высоте. Лекция 4
1. Лекция 4
Графовые модели программы.Алгоритм оптимизации информационного
графа по ширине пи высоте
2.
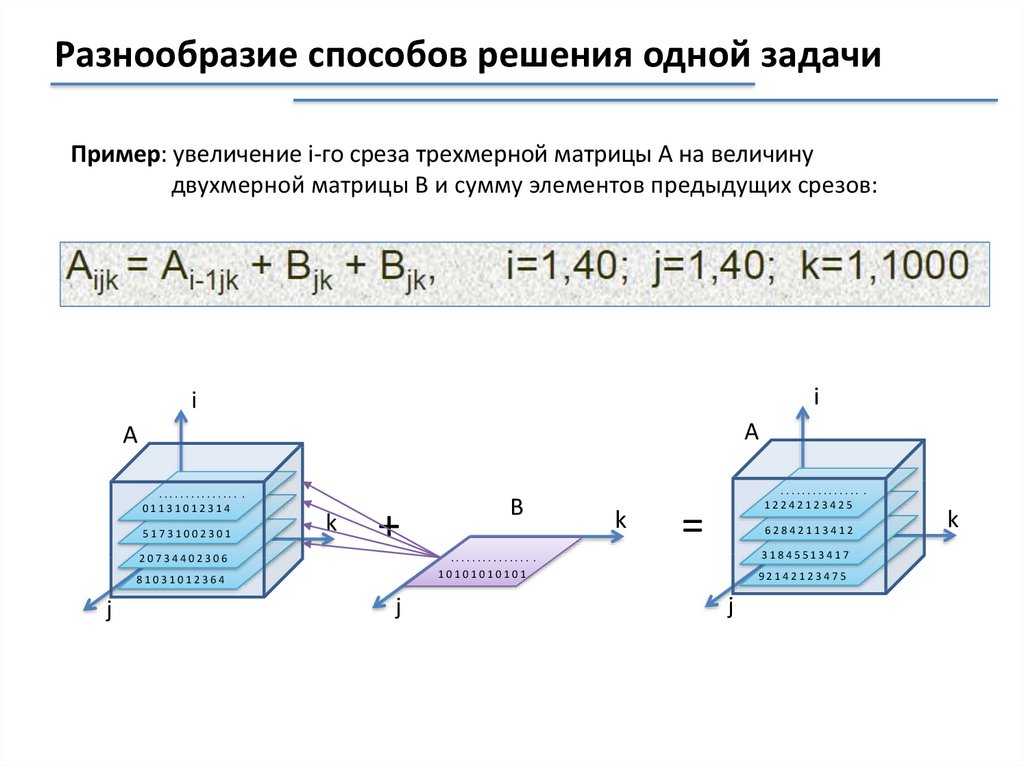
Разнообразие способов решения одной задачиПример: увеличение i-го среза трехмерной матрицы А на величину
двухмерной матрицы В и сумму элементов предыдущих срезов:
i
i
А
А
............... .
01131012314
51731002301
k
+
k
=
62842113412
31845513417
............... .
10101010101
20734402306
81031012364
j
В
............... .
12242123425
j
92142123475
j
k
3.
Способ 1 организации суммирования4.
Способ 2 организации суммирования5.
Пример 2 Умножение матриц1. Возможен ли другой порядок?
2. Нужен ли другой порядок?
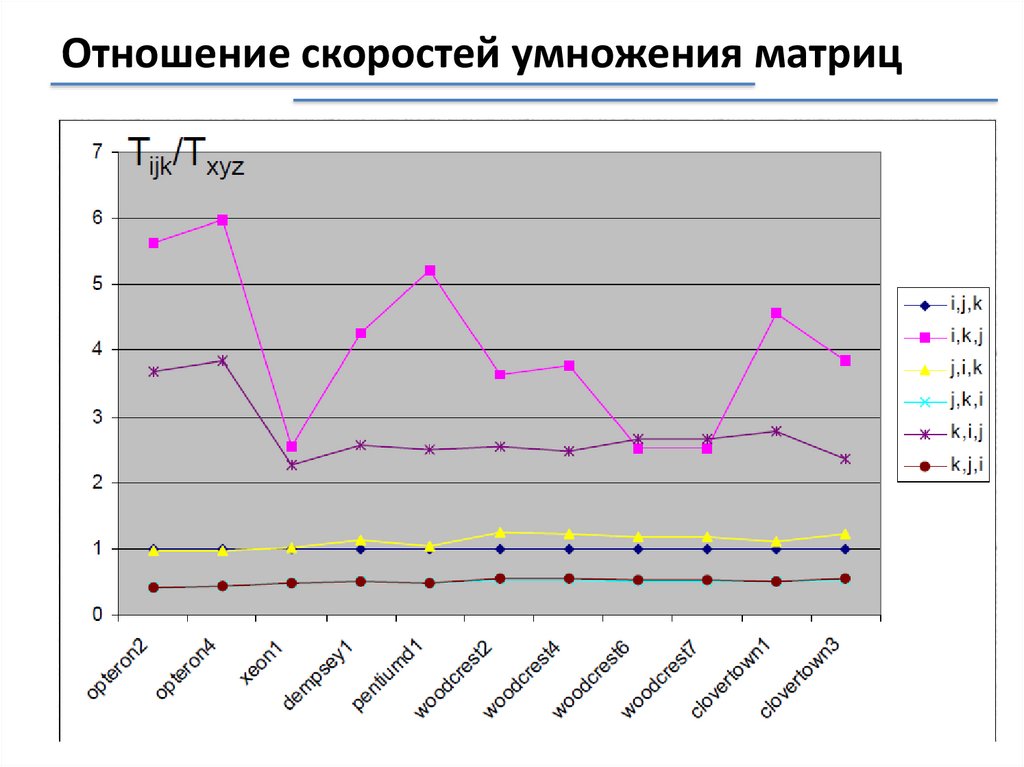
6.
Отношение скоростей умножения матриц7.
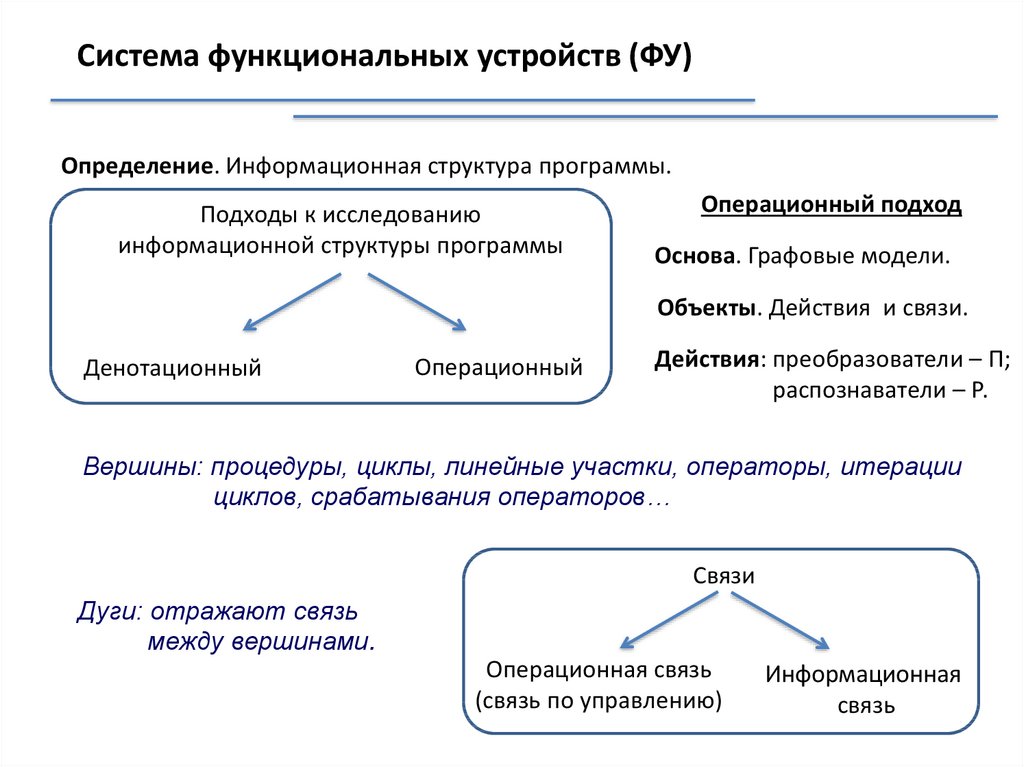
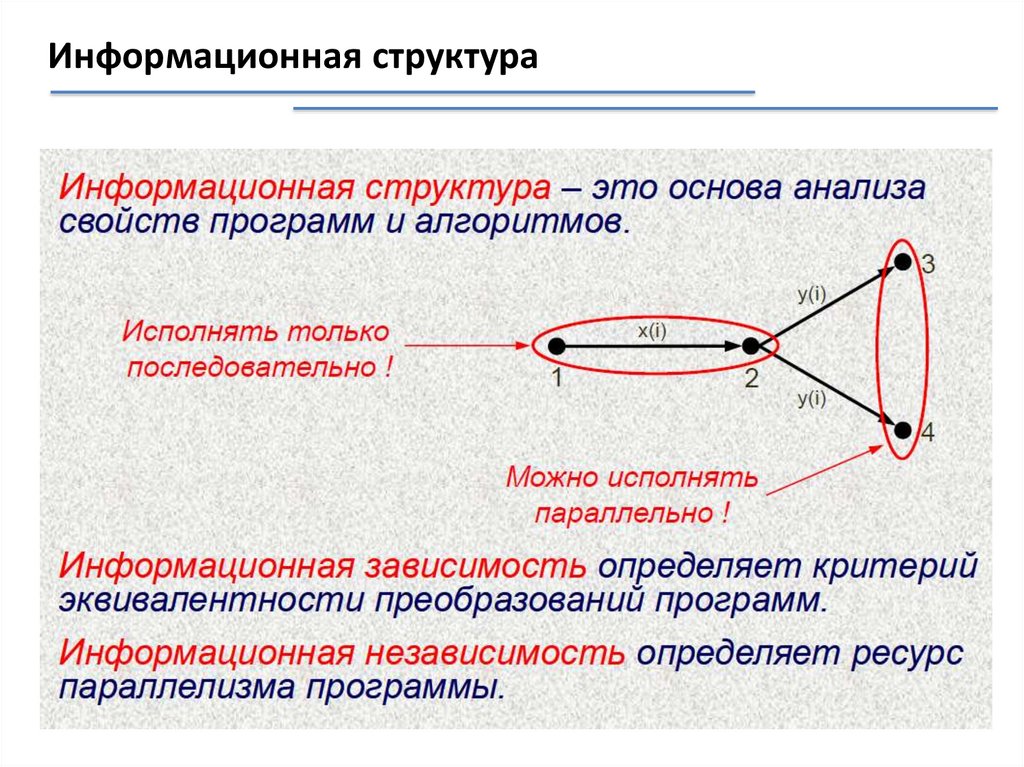
Система функциональных устройств (ФУ)Определение. Информационная структура программы.
Подходы к исследованию
информационной структуры программы
Операционный подход
Основа. Графовые модели.
Объекты. Действия и связи.
Денотационный
Операционный
Действия: преобразователи – П;
распознаватели – Р.
Вершины: процедуры, циклы, линейные участки, операторы, итерации
циклов, срабатывания операторов…
Связи
Дуги: отражают связь
между вершинами.
Операционная связь
(связь по управлению)
Информационная
связь
8.
Операционная связьДуги: операционная связь
Две вершины A и B соединяются направленной дугой тогда и только
тогда, когда вершина B может быть выполнена сразу после вершины A.
А
В
Операционная связь= связь по передаче управления.
Пример:
x(i) = a + b(i)
(1)
y(i) = 2*x(i) – 3
(2)
t1 = y(i)*y(i) + 1
(3)
t2 = b(i) – y(i)*a
(4)
9.
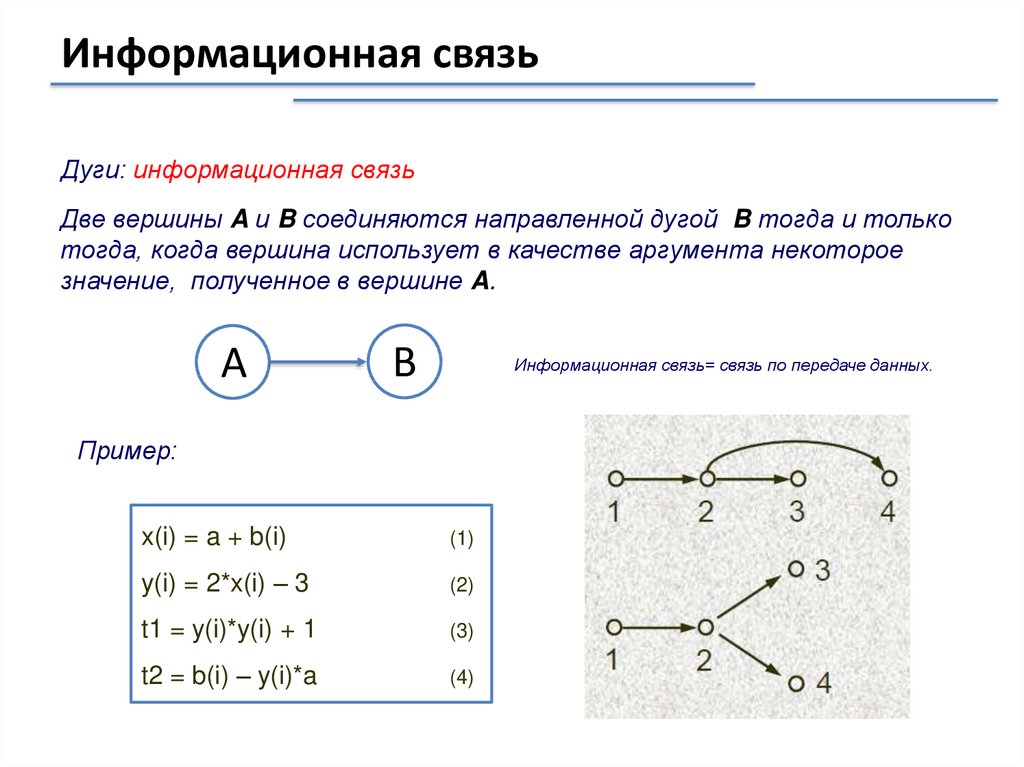
Информационная связьДуги: информационная связь
Две вершины A и B соединяются направленной дугой B тогда и только
тогда, когда вершина использует в качестве аргумента некоторое
значение, полученное в вершине A.
А
В
Информационная связь= связь по передаче данных.
Пример:
x(i) = a + b(i)
(1)
y(i) = 2*x(i) – 3
(2)
t1 = y(i)*y(i) + 1
(3)
t2 = b(i) – y(i)*a
(4)
10.
Пример: Система линейных уравненийДано:
СЛАУ: Ax=b;
A(nxn) – левая двухдиагональная матрица;
ai – диагональные элементы, i=1..n;
ci – поддиагональные элементы, i=1..n, c1 = 0;
bi – правые части, i=1..n;
xi – координаты решения, i=1..n.
Найти:
максимальную координату вектора-решения.
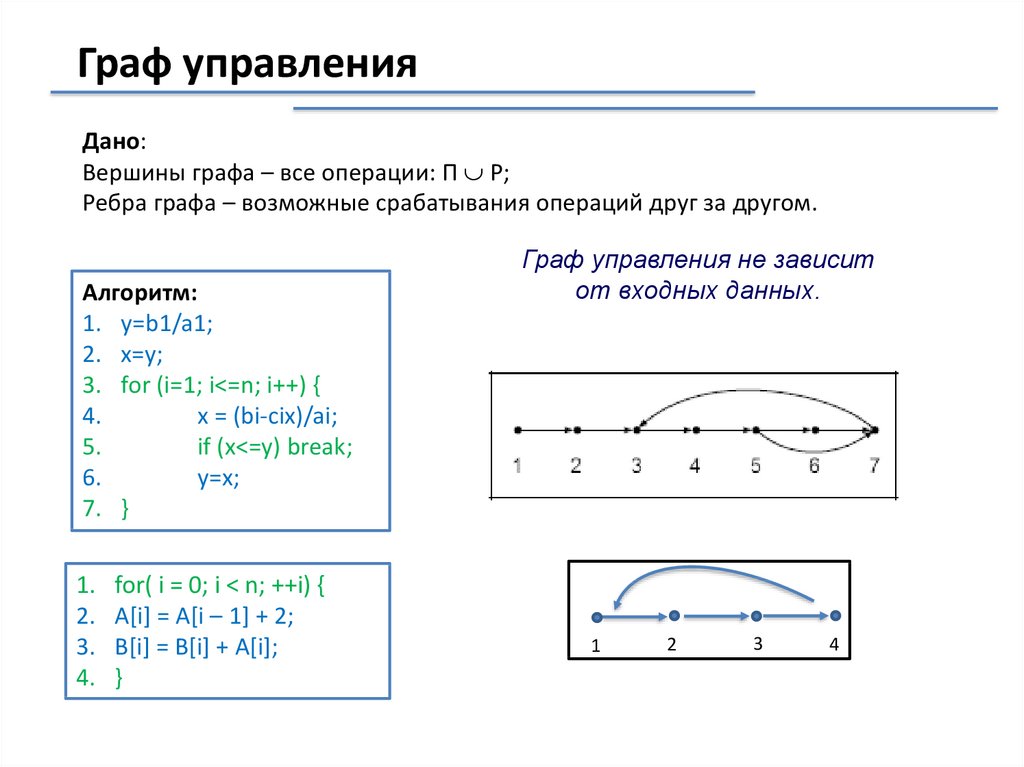
Алгоритм:
1. y=b1/a1;
2. x=y;
3. for (i=1; i<=n; i++) {
4.
x = (bi-ci*x)/ai;
5.
if (x<=y) break;
6.
y=x;
7. }




























 programming
programming








