Similar presentations:
Поиск в информационном массиве. Тема 4
1. Поиск в информационном массиве
• Информационный массив: k1:a1,…,kn:an,ki kj
– ki – ключи
– ai – информационные элементы
• Задача: найти элемент с ключом k.
• Природа информационных элементов
может быть произвольной.
• Возможность эффективного поиска
может существенно зависеть от природы
ключей.
2. Линейный поиск
• Условие: Ключи можно сравниватьтолько на равенство
• Метод: Последовательный перебор,
метод Британского музея, …
• Сложность в худшем: O(n), когда
искомого элемента нет
3. Линейный поиск
• Сложность в среднем: пусть всевероятности появления ki одинаковы и равны
p, а вероятность отсутствия равна q:
np+q = 1
• Тогда
n(n 1)
Tср (n) ip nq p
n(1 np)
2
i 1
n(1 n)
p
n
2
n
4. Линейный поиск
• Случай p=1/n(ищем только то,
что обязательно
найдём)
n 1
Tср (n)
2
• Случай p=0 (вряд
ли найдём)
Tср ( n) n
5. Бинарный поиск
• Условие: На ключах задан линейный порядок• Метод:
l:=1; r:=n; found:=false;
while l<=r and not found do
m := (l+r)/2
if k=km then
found := true
// km – искомый ключ
else if k<km then
r := m-1
else
l := m+1
6. Бинарный поиск
• Сложность в худшем:– Выходим из цикла по l>r
– На каждой итерации 2 сравнения
– На каждой итерации выбираем большую на 1 по
размеру «половину»
– Худший (наименьший) размер массива,
требующий k итераций
nk = 1 + nk-1 + (nk-1-1) = 2nk-1
n1 = 1
• Таким образом, nk=2k-1
• Т(n) = 2(log(n)+1)
7. Бинарные (двоичные) деревья
<ki
<
function find(k,T): bool
if T пусто then
find := false
else if T.key = k then
find := true
else if T.key < k then
find := find(k,T.left)
else
find := find(k,T.right)
8. Бинарные деревья
• Сложность в худшем:– ищем максимальный
– левое поддерево
всегда пусто
• 2 сравнения на каждой
итерации:T(n)=2n
k1
k2
kn-1
kn
9. 2-3-деревья
• У каждого не листа либо2, либо 3 сына (1 быть не
может)
• Все пути от корня до
листьев – одинаковой
длины
M1 <
• Ключи – в листьях,
упорядочены
• Для каждого не листа
известны максимальные
ключи для первого и
второго поддеревьев
k1 k2
M2 <
kn-1 kn
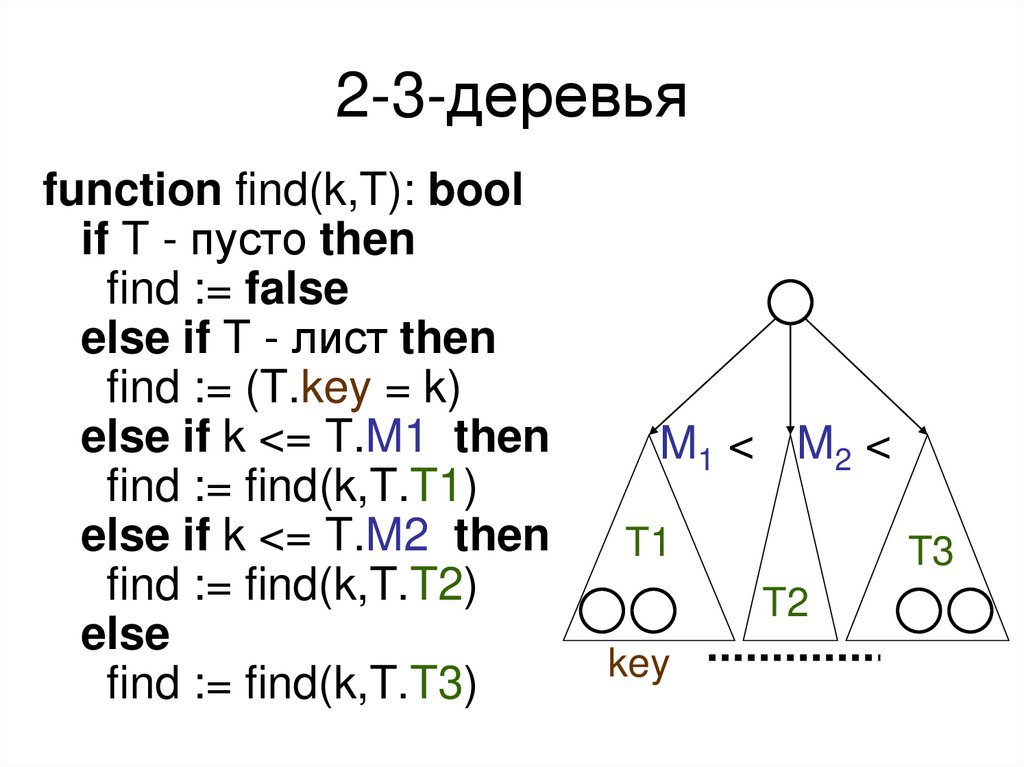
10. 2-3-деревья
function find(k,T): boolif T - пусто then
find := false
else if T - лист then
find := (T.key = k)
else if k <= T.M1 then
find := find(k,T.T1)
else if k <= T.M2 then
find := find(k,T.T2)
else
find := find(k,T.T3)
M1 < M2 <
T1
T3
T2
key
11. 2-3-деревья
• Cложность. Пусть h – высота дерева.– Количество ключей (количество листьев)
2h n 3 h
– Следовательно h log(n)
– Количество сравнений: 2*log(n)-1
– T(n) = O(log n)
12. Вставка в 2-3-дерево
32
5
3
2
3
2
3
5
4
2
3
4
5
2
3
4
5
13. Вставка в 2-3-дерево
• Сложность:– Поиск места для вставки (вниз по дереву):
O(log(n))
– Добавление новых промежуточных вершин
(вверх по дереву): O(log(n))
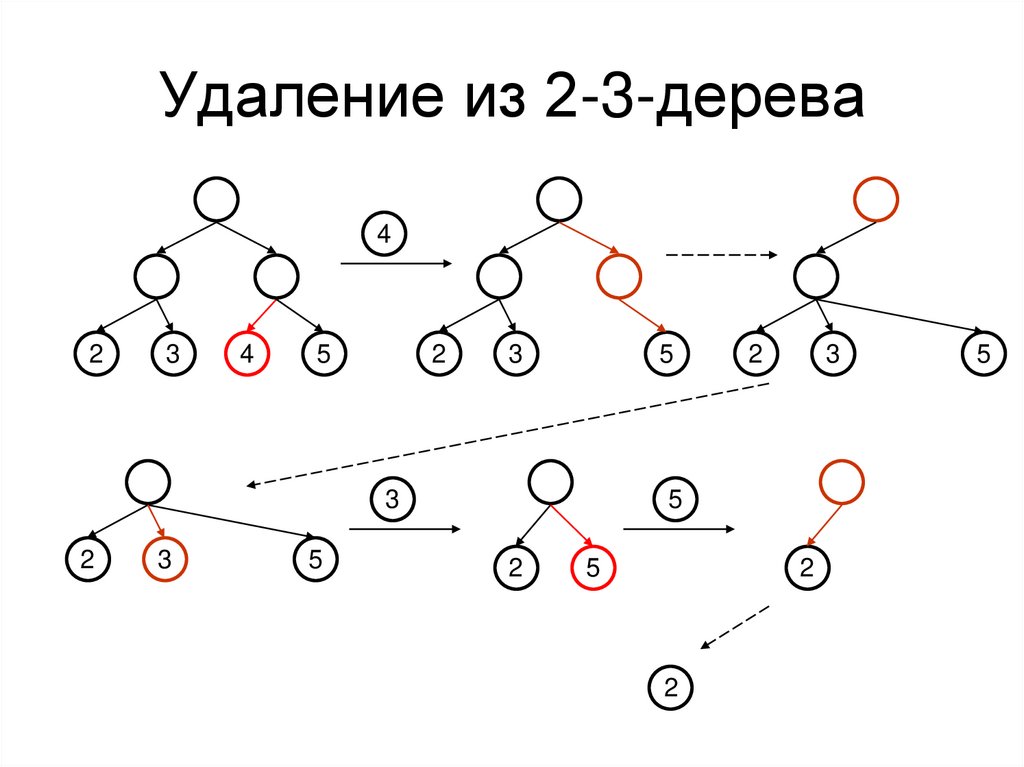
14. Удаление из 2-3-дерева
42
3
4
5
2
3
5
3
2
3
5
2
3
5
2
5
2
2
5
15. Обобщение: B-деревья
• B-дерево (не путать с бинарнымидеревьями!) степени m:
– каждый не лист имеет по крайней мере m/2
и не более m сыновей.
– Для каждого не листа задан массив
разделяющих значений M1,…,Mm-1
16. B-деревья
function find(k,T): boolif T - пусто then
find := false
else if T - лист then
find := (T.key = k)
else
i := max{ j : 1..m-1 | T.key <= T.Mj}
if i – определено then
find := find(k,T.Ti)
else
find := find(k,T.Tn)
17. B-деревья
• Сложность– Высота дерева степени m с n листьями не
превосходит logm(n)
– При каждом рекурсивном вызове все
сравнения содержатся в вычислении
max{ j : 1..m-1 | T.key <= T.Mj}
– Поскольку Mi упорядочен, то бинарный
поиск требует log2(m) сравнений
– Итого: logm(n) * log2(m) = log2(n) сравнений
18. АВЛ-деревья
• АВЛ-дерево:– Двоичное дерево поиска
– Баланс вершины v с двумя
(возможно пустыми)
поддеревьями T1 и T2:
balance(v) = h(T1) – h(T2)
– Для любой вершины
|balance(v)| 1
v
T1
1
T2
19. АВЛ-деревья
• Лемма. Пусть высота АВЛ-дерева равна h, аколичество вершин – n. Тогда
1 5
2
h 1
n 2h 1 1
• Доказательство.
– Верхняя оценка: очевидно - полное дерево.
– Нижняя оценка: для заданной высоты h построим
АВЛ-дерево с минимальным количеством вершин
m(h).
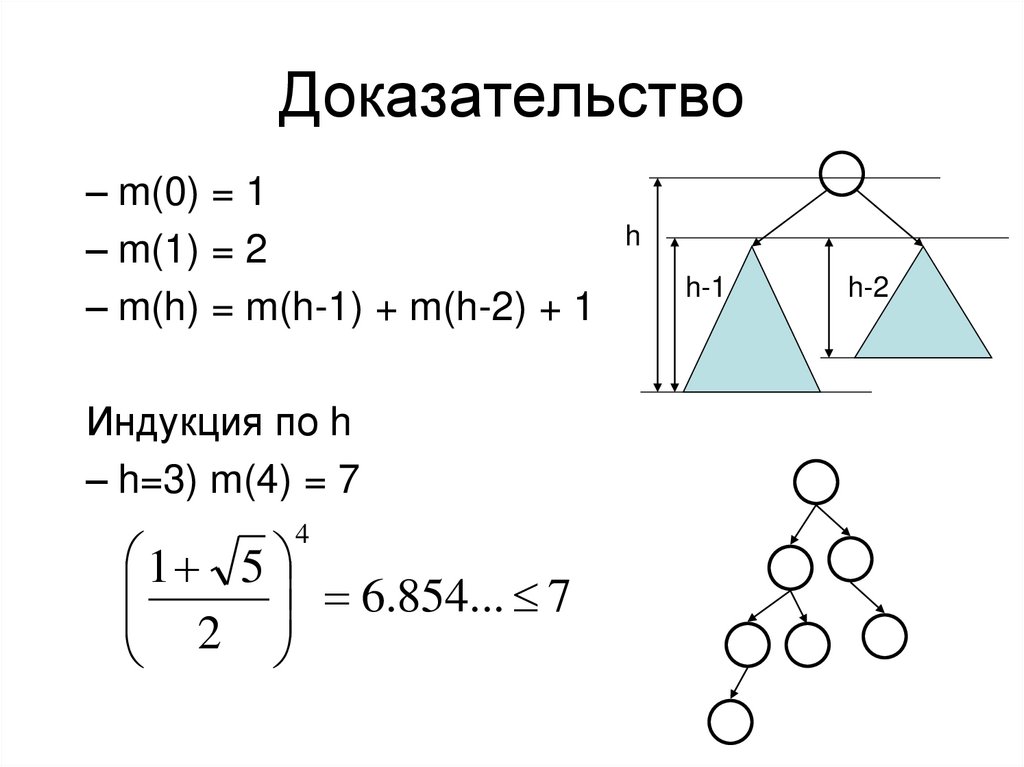
20. Доказательство
– m(0) = 1– m(1) = 2
– m(h) = m(h-1) + m(h-2) + 1
Индукция по h
– h=3) m(4) = 7
4
1 5
6.854... 7
2
h
h-1
h-2
21. Доказательство
– Шаг индукции) Заметим, что a– корень уравнения
x2 =x+1
– Тогда
m(h+1) = m(h) + m(h-1) + 1
ah+1 + ah + 1 =
= ah(a+1) + 1 =
= ah+2 +1 >
> ah+2
• Конец доказательства.
1 5
a
2
22. Вставка в АВЛ-дерево
1. Вставляем новую вершину в деревопоиска: O(log(n))
2. Ищем вершину, для которой
нарушился баланс: O(log(n))
3. Если нашли, то восстанавливаем
баланс – O(1), применяя либо
простое вращение, либо
двойное вращение
23. Простое вращение
BA
A
B
T3
T1
T2
T1
T2
T3
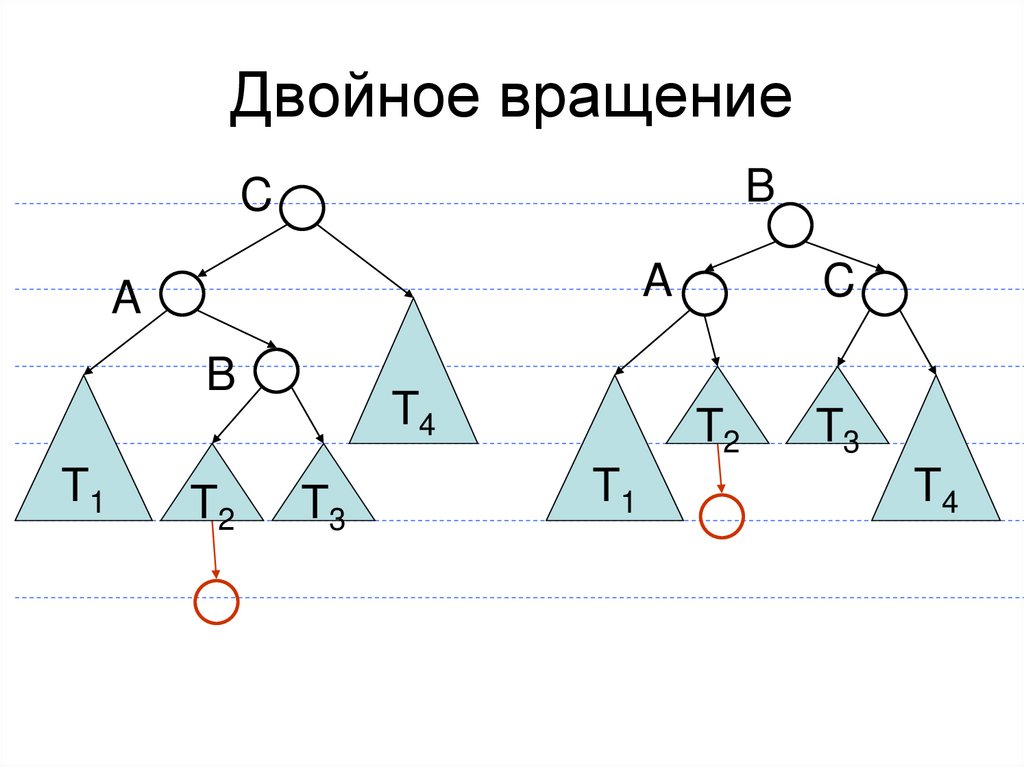
24. Двойное вращение
BC
A
A
B
T1
T2
T4
T3
C
T2
T1
T3
T4
25. Метод расстановки
• Функция расстановки (hash-функция):function hash(k) : 1..M;
– Достаточно простая (вычислима за
константное время)
– «Равномерная» - выдаёт значения из
диапазона 1..M c одинаковой
вероятностью.
26. Метод расстановки
• Таблицарасстановки (hashтаблица):
type HashTable =
array[1..M] of
list of
(k:Key,
a:Elem);
1
…
…
2
…
…
3
…
…
…
hash(k) = h
h
…
M
…
k:a …
27. Метод расстановки
• function find(k,HT): Elemfor each e in HT[hash(k)]
if e.k = k then
return e.a;
return nil;
• proc insert(k,a,HT)
HT[hash(k)].append((k,a));
28. Метод расстановки
• Сложность в худшем –последовательный перебор: O(n)
1
…
" i :hash(ki) = h
h
k1:a1 k2:a2 … kn:an
…
M
29. Метод расстановки
• Сложность в среднем:– Пусть qi – вероятность того, что hash(k) = i
– pi(l,n) – длина списка HT[i] равна l
l l
n l
n i
i
C q (1 q )
– P(l) – хотя бы один список имеет длину l
M
q C q (1 q )
i
i 1
M
l l
n i
n l
i
C q (1 qi )
i 1
l l 1
n i
n l
30. Метод расстановки
• Сложность в среднем – мат. ожидание Pn
lP (l )
l 1
n
M
l 1
i 1
M
n
l C q (1 qi )
l l 1
n i
lC q (1 qi )
i 1 l 1
l l 1
n i
n l
n l
31. Метод расстановки
ll 1
• Заметим, что
lC n nCn 1
• Подставляя и вынося nqi2, получаем
M
n
n q C q (1 qi )
i 1
2
i
l 1
l 1 l 1
n 1 i
n l
• Сумма по l – бином Ньютона для qi и (1-qi), т.е.
равна 1. Остаётся
M
n q
i 1
2
i
32. Метод расстановки
• По неравенству Коши-Буняковского длявекторов (1,1,…,1) и (q1,q2,…,qM) имеем
2
M
2
qi M qi
i 1
i 1
M
M
1 M q
i 1
M
2
i
1
q
M
i 1
2
i
33. Метод расстановки
• Таким образомn
Tср (n)
M
• Равенство достигается при
1
q1 q2 ... qM
M
34. Сортировка
• Классификация по применению– Доступ к элементам
• Внутренняя – доступ ко всем элементам одинаков
(массив)
• Внешняя – время доступа зависит от индекса
– Использование памяти
• На месте – размер рабочей памяти не зависит от размера
массива
• С переписыванием – использование временных
дополнительных массивов
– Дополнительные предположения о природе ключей
• Ограниченный диапазон
• Строки
35. Сортировка
• Классификация по поведению– Естественное поведение – на почти
упорядоченных массивах работает быстрее
– Сохранение порядка элементов с равными
ключами
36. Сортировка
• Оценка сложности– По количеству сравнений
– По количеству перемещений элементов
– ...
37. Сортировка
• Классификация по методам– Включением: взять очередной элемент и
поставить на место
– Выбором: найти элемент, который нужно
поставить на очередное место
– Обменом: найти и поменять местами пару
элементов
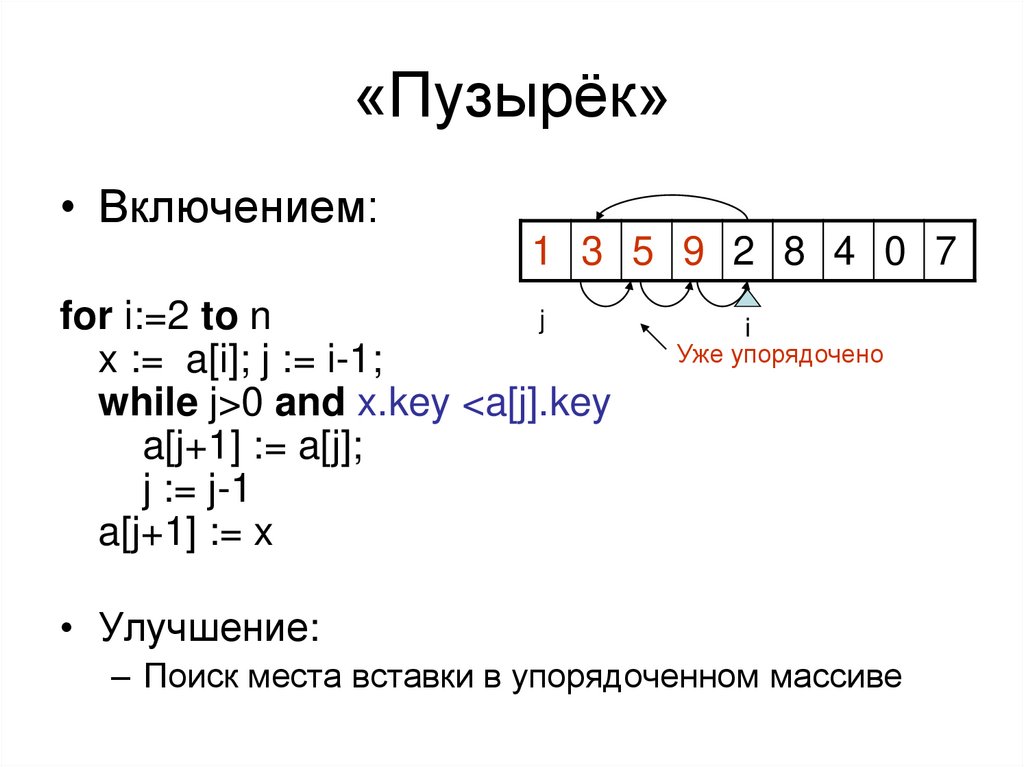
38. «Пузырёк»
• Включением:1 3 5 9 2 8 4 0 7
j
for i:=2 to n
x := a[i]; j := i-1;
while j>0 and x.key <a[j].key
a[j+1] := a[j];
j := j-1
a[j+1] := x
i
Уже упорядочено
• Улучшение:
– Поиск места вставки в упорядоченном массиве
39. «Пузырёк»
• Выбором:1 2 3 4 9 8 5 0 7
for i:=1 to n-1
x := a[i]; k := i;
for j:=i+1 to n
if a[j].key < x.key
k := j;
x := a[j];
if k != i then
a[k] := a[i];
a[i] := x;
k
i
Уже упорядочено
40. «Пузырёк»
• Обменом:1 2 3 4 9 8 5 0 7
for i:=2 to n-1
for j:=n downto i
if a[j-1].key > a[j].key then
a[j-1] :=: a[j]
j
i
Уже упорядочено
• Улучшение:
– Запоминать размер упорядоченного конца
– Вовремя остановиться
41. Дерево решений
a<b+
b<c
a<c
+
+
c<a
a b c
+
+
c a b
c<b
b a c
a c b
c b a
b c a
42. Общая оценка в худшем
• Теорема. Всякий алгоритм,упорядочивающий массив длины n,
основываясь на сравнениях, требует в
худшем не менее O(n log(n))
сравнений.
• Доказательство.
– Сложность в худшем – высота h дерева
решений.
– Листьев в дереве решений n! 2h
43. Доказательство
– Следовательно log(n!) h– По формуле Стирлинга:
– Следовательно,
n
n!
e
n
2 n
log( n!)
log( 2 ) log( n)
n log( n) log( e)
2
O(n log( n))
• Конец доказательства.
44. Сортировка слиянием
while i<=mproc sort(l,r)
b[k]:=a[i]; i:=i+1;
if r>l then
k:=k+1;
m:= (l+r)/2; k := l;
while j<=r
sort(l,m);
b[k]:=a[j]; j:=j+1;
sort(m+1,r);
k:=k+1;
while i<=m and j<=r
a[l..r] := b[l..r];
if a[i].key<a[j].key then
b[k]:=a[i]; i:=i+1;
a: … 2 3 5 0 1 6 8 …
else
l
i m
j r
b[k]:=a[j]; j:=j+1;
b: … 0 1 2 ? ? ? ? …
k:=k+1;
k
45. Сортировка слиянием
• Сложность T(n), где n=l-r+1– Пусть n=2k
– Сложность sort(l,m) и sort(m+1,r): T(n/2)
– Сложность слияния: n-1
– T(1) = 0
– T(n) = 2T(n/2) + n-1 = 2T(2k-1) +2k-1 <
< 2T(2k-1) +2k = 2(2T(2k-2) +2k-1-1) + 2k <
< 4T(2k-2) +2*2k = 4(2T(2k-3) +2k-2-1) + 2*2k <
< 8T(2k-3) +3*2k = 8(2T(2k-3) +2k-2-1) + 3*2k <
….
< 2kT(20) + k2k = k2k = n log(n)
46. Сортировка слиянием
• Ёмкостная сложность:– Дополнительный массив b: O(n)
– Рекурсия: O(log(n))
47. Общая оценка в среднем
• Теорема. Если вероятность всехперестановок одинакова, то всякий алгоритм,
упорядочивающий массив длины n,
основываясь на сравнениях, требует в
среднем не менее O(n log(n)) сравнений.
• Доказательство.
– Определим D(t) = сумма глубин всех листьев.
– Определим d(m) = min D(t) по всем деревьям t c m
листьями
– Позже покажем, что d(m) m log(m)
48. Доказательство
– Пусть A – некоторый алгоритм, tA – дерево егорешений на массиве длины n
– Удаляем все недостижимые вершины, т.е. те
«вопросы», ответы на которые можно вывести из
предыдущих.
– Осталось n! листьев, каждая с вероятностью 1/n!
– Тогда
D(t A ) n!log( n!)
T ( n)
O(n log( n))
n!
n!
A
ср
• Конец доказательства.
49. d(m) ³ m log(m)
d(m) m log(m)• Лемма. " m : d(m) m log(m).
• Доказательство. Обозначим Tm – множество
деревьев с m листьями. Индукцией по m:
m=1) d(m) = m log(m) = 0
Шаг) Пусть в дереве t имеется m листьев: i - в
правом t1 и (m-i) – в левом t2.
– Тогда D(t) = i+D(t1) + (m-i)+D(t2) =
= m + D(t1) + D(t2)
– Т.е. d(m) = mini min{m + D(t1) + D(t2) | t1 Ti,t2 Tm-i}
50. Доказательство
– min{m + D(t1) + D(t2) | t1 Ti,t2 Tm-i} == m + min{D(t1) | t1 Ti} + min{D(t2) | t2 Tm-i} =
= m + d(i) + d(m-i)
– Тогда по предположению индукции
d(m) m + mini (i log(i) + (m-i) log(m-i))
– mini достигается при i=m/2
– Значит d(m) m+2 (m/2) log(m/2) =
= m(1 + log(m) – log(2)) = m log(m)
• Конец доказательства.
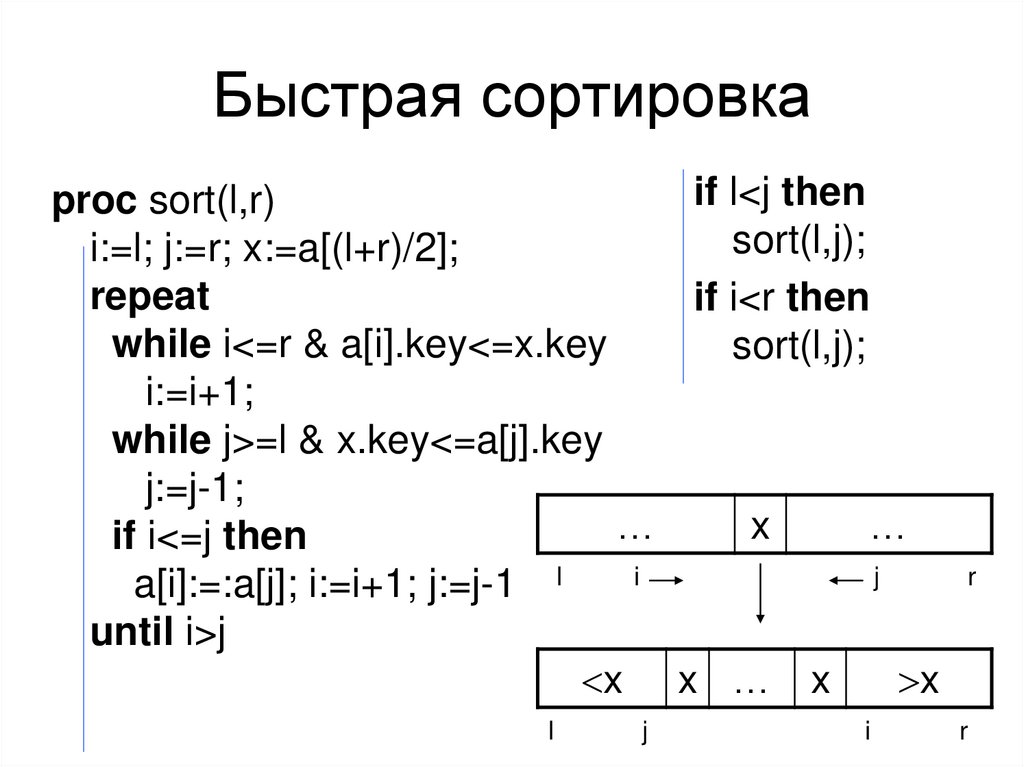
51. Быстрая сортировка
if l<j thenproc sort(l,r)
sort(l,j);
i:=l; j:=r; x:=a[(l+r)/2];
repeat
if i<r then
while i<=r & a[i].key<=x.key
sort(l,j);
i:=i+1;
while j>=l & x.key<=a[j].key
j:=j-1;
…
x
…
if i<=j then
i
j
r
a[i]:=:a[j]; i:=i+1; j:=j-1 l
until i>j
<x x … x
>x
l
j
i
r
52. Быстрая сортировка
• Сложность в худшем : всегда в качестве xпопадается минимальный элемент: O(n2) как
в полном переборе
• Сложность в лучшем (на упорядоченном
массиве): всегда в качестве x попадается
минимальный серединный элемент
(медиана): O(n log(n)) как в сортировке
слиянием.
• Улучшение: (приблизительный) поиск
медианы, например, из 3-х произвольно
выбранных элементов.
53. Быстрая сортировка
• Сложность в среднем: в качестве xпопадается p-ый наименьший
(предположительно) с вероятностью 1/n.
n
1
T (n) Cn (T ( p 1) T (n p ))
p 1 n
2 n 1
Cn T (i )
n i 0
54. Быстрая сортировка (сложность в среднем)
• Пусть T(0) = T(1) = b• Индукцией по n покажем, что T(n) K n ln(n),
где K = 2b + 2C
• n=2)
1
2
T (2) 2C T (i)
2 i 0
2C 2b
55. Быстрая сортировка (сложность в среднем)
• Шаг индукции)n 1
4b 2
T (n) Cn
T (i )
n n i 2
n 1
4b 2 K
Cn
i ln( i )
n
n i 2
56. Быстрая сортировка (сложность в среднем)
• Так как i ln(i) монотонно возрастает, тоn 1
n
i 2
2
i ln( i) x ln( x)dx
2
2
n ln( n) n
2
4
57. Быстрая сортировка (сложность в среднем)
• Подставляя, получаем4b 2 K n 2 ln n n 2
T (n) Cn
n
n 2
4
4b
n
Kn ln n Cn
K
n
2
• Достаточно показать, что
4b
n
n
Cn
K 2b 2C Cn bn
n
2
2
58. Быстрая сортировка (сложность в среднем)
• Что сводится к4b
bn
n
и далее к предположению, что 2 n.
• Конец доказательства.
59. Быстрая сортировка
• Ёмкостная сложность в худшем:– Глубина рекурсии: n
• Идея усовершенствования:
– Сортировка подчастей – заключительная
часть каждого вызова.
– Неважно в каком порядке сортировать
правую и левую части – сразу (без
рекурсии) начнём с большей, и отложим в
стек запрос на сортировку меньшей.
60. Быстрая сортировка
proc sort(l,r)while (r>l)
i:=l; j:=r; x:=a[(l+r)/2];
repeat
…..
until i>j
if j-l < r-i then
sort(l,j);
l:=i;
else
sort(i,r);
r:=j;
– Глубина стека
запросов: O(log(n))






















































 programming
programming








