Similar presentations:
Дискретная математика. Замкнутый класс
1. Дискретная математика
2. Замкнутый класс
• Система функций называетсязамкнутым классом, если
любая суперпозиция функций
системы снова принадлежит
системе .
3. Пример 1
• Множество всех конъюнкций K1– замкнутый класс.
f x, y xy K1 , g x,z xz K1 ,
h x, y,t xyt K1 .
w x, y,z,t f g x,z ,h x, y,t
xz xyt xzxyt xyzt K1
4. Пример 2
• Множество всех дизъюнкций K2– замкнутый класс.
f x,z x z K 2 , g y,z y z K 2 ,
h y,z,t y z t K 2 .
v x, y,z h y,g y,z , f x,z
y y z x z y y z x z
x y z K2
5. Пример 3
• Множество всех полиномов ЖегалкинаK3 – замкнутый класс.
f x,z x z 1 K 3 , g y,z y z K 3 ,
h x,z,t x z t K 3 .
w x, y,z,t f h x,z,t ,g y,z
x z t y z 1
x y z z t 1
x y t 1 K3
6. Замыкание
• Замыканием сиcтемыфункций называется
система [ ], состоящая из
всех функций системы и
всех суперпозиций
функций системы .
7. Функционально полные системы
Система функций называетсяфункционально полной (ФП), если
через суперпозиции функций этой
системы можно выразить любую
логическую функцию.
8. Замечание 1
Если система функцийявляется замкнутым классом,
то есть =K,
тогда она равна своему
замыканию:
K K
9. Замечание 2
Если система функцийявляется функционально полной,
тогда ее замыкание равно всему
множеству логических функций:
P2
10. Пример 1
Пусть система0 , , -
множество булевых операций
(базис Буля).
0 – ФП, так как любая логическая
функция может быть выражена
Булевой формулой (БФ).
11. Пример 2
Система 0 является избыточной.Дизъюнкцию можно выразить через
конъюнкцию и отрицание:
x y x y
Конъюнкцию можно выразить через
дизъюнкцию и отрицание:
x y x y
12. Продолжение примера 2
Откуда:1 , ФП
2 , ФП
13. Замечание:
• За не избыточностьсистемы приходится
платить избыточностью
формул.
14. Пример 3
Пусть булева формула имеет вид:F0 x, y, z xy xz
Тогда, в системе 1 она
принимает вид:
F1 x, y, z xy xz xy xz
15. Пример 4
F0 x, y, z xy xzТогда, в системе 2 она
принимает вид:
F2 x, y, z x y x z
x y x z
16. Пример 6
Система4
- функционально полна.
Это следует из того, что через штрих
Шеффера можно выразить функции
ФП системы:
1 , .
17. Продолжение примера 6
Отрицание выразим по формуле:x xx
Конъюнкцию выразим по формуле:
x y x y x y x y .
18. Продолжение примера 6
Убедимся в истинности равенства:x xx
0 1, 0 0 1
1 0, 11 0.
19. Пример 7
Система4
- функционально полна.
Это следует из того, что через стрелку
Пирса можно выразить функции ФП
системы:
2 , .
20. Продолжение примера 7
Отрицание выразим по формуле:x x x
Дизъюнкцию выразим по формуле:
x y x y x y x y .
21. Продолжение примера 7
Убедимся в истинности равенства:x x x
0 1, 0 0 1
1 0, 1 1 0.
22. Теорема 1
Если через функции системыможно выразить функции булева
базиса
0 , , ,
то система - функциональна полна.
Тогда говорят, что система -
сводится к системе 0:
0.
23. Следствие
1 , 0 , ,2 , 0 , ,
3
1 ,
4 2 ,
24. Теорема 2
Если через функции системыможно выразить функции некоторой
функционально полной системы
f1 , f 2 , ..., f k ,
то система - функциональна полна.
.
25. Следствие
Таким образом, доказательствофункциональной полноты
произвольной системы функций
можно строить путем сведения ее к
некоторой системе, функциональная
полнота которой доказана.
26. Функциональная полнота в слабом смысле
Система функций называетсяфункционально полной в слабом
смысле (сФП),
если она будет функционально полной
после добавления констант 0 и 1.
0,1 ФП.
27. Функциональная полнота в слабом смысле
Система функций, сФП
Среди функций, образующей AG, нет
константы 1.
Но ровно половина всех полиномов
содержит слагаемое 1.
5 , ,1 ФП.






















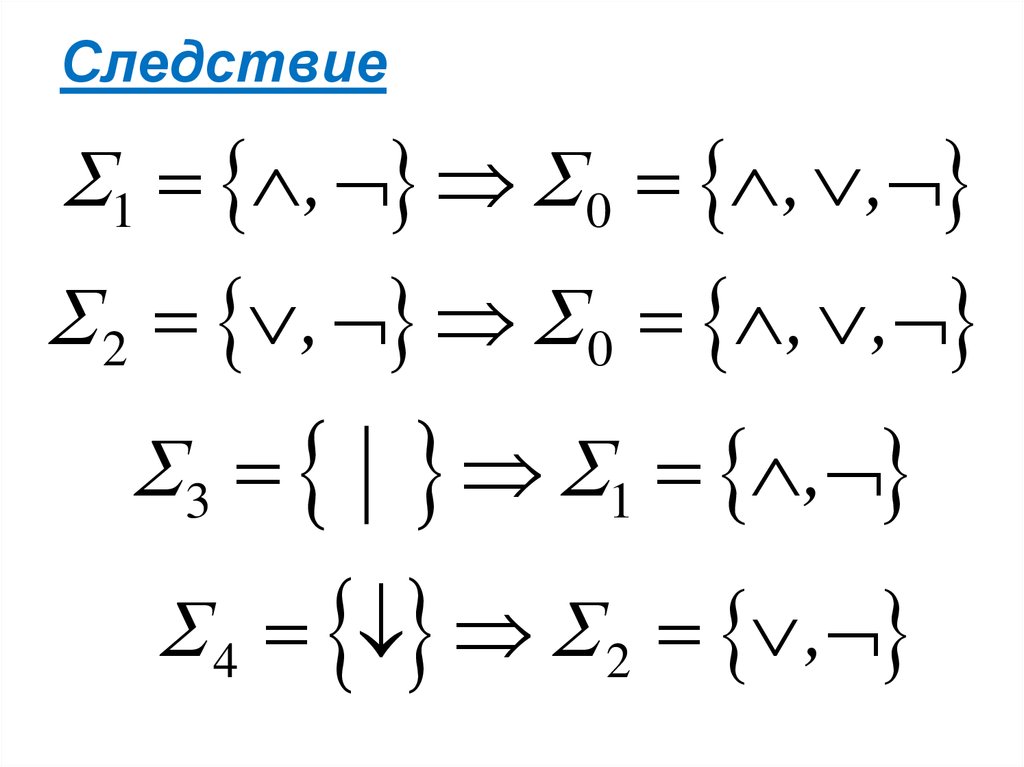




 mathematics
mathematics








