Similar presentations:
Теорема Пифагора
1. Классная работа
23.11.2017Классная работа
2.
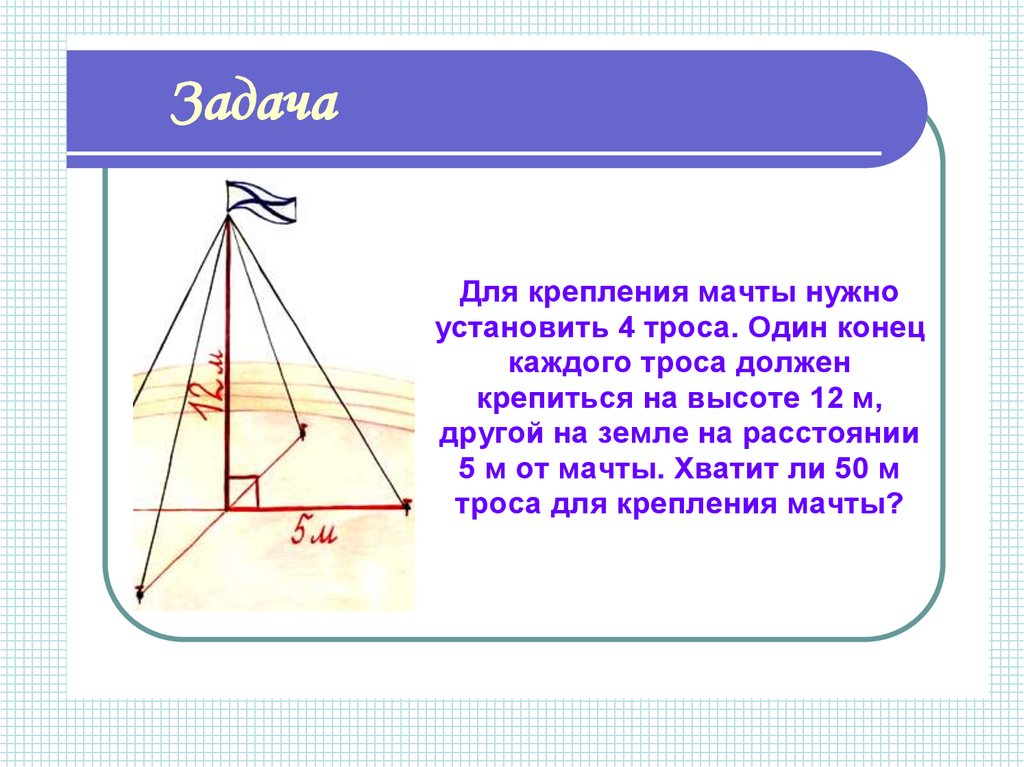
ЗадачаДля крепления мачты нужно
установить 4 троса. Один конец
каждого троса должен
крепиться на высоте 12 м,
другой на земле на расстоянии
5 м от мачты. Хватит ли 50 м
троса для крепления мачты?
3. Классная работа
23.11.2017Классная работа
4.
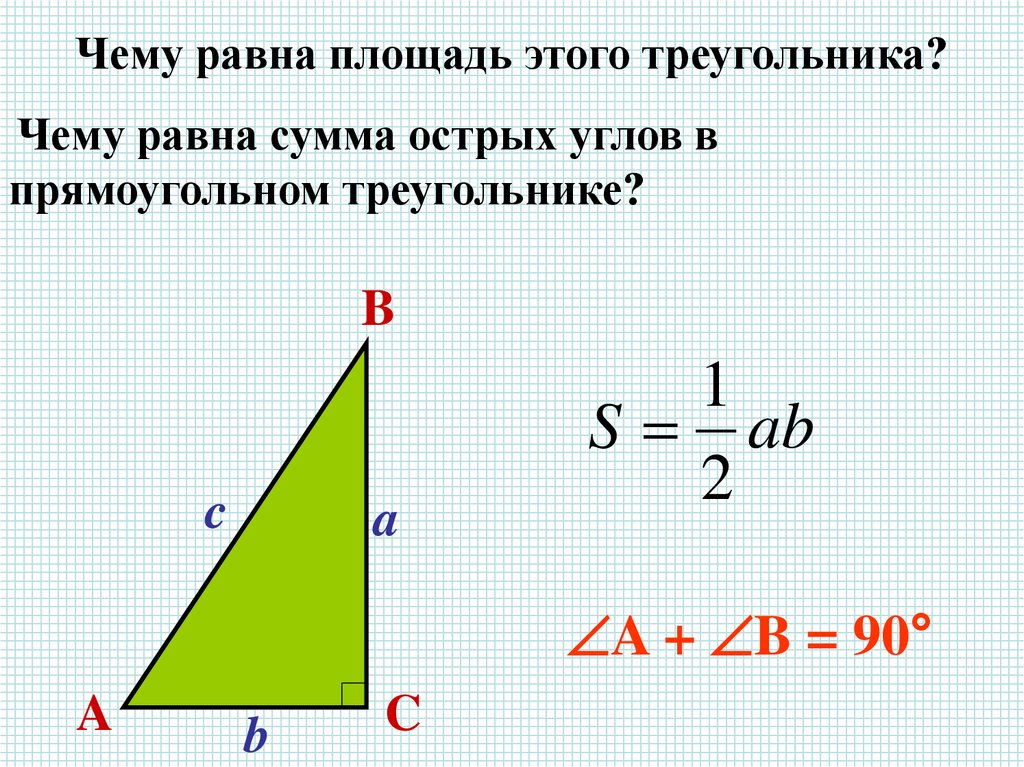
Чему равна площадь этого треугольника?Чему равна сумма острых углов в
прямоугольном треугольнике?
B
c
a
1
S ab
2
A + B = 90°
A
b
C
5.
CB
D
A
E
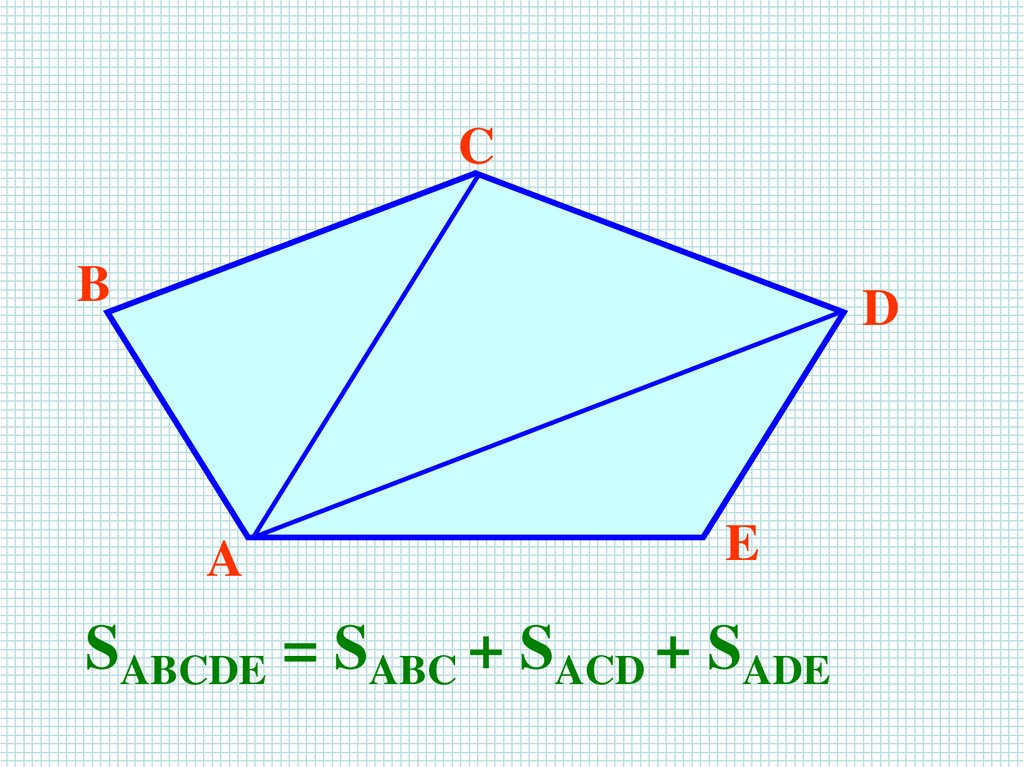
SABCDE = SABC + SACD + SADE
6.
31
2
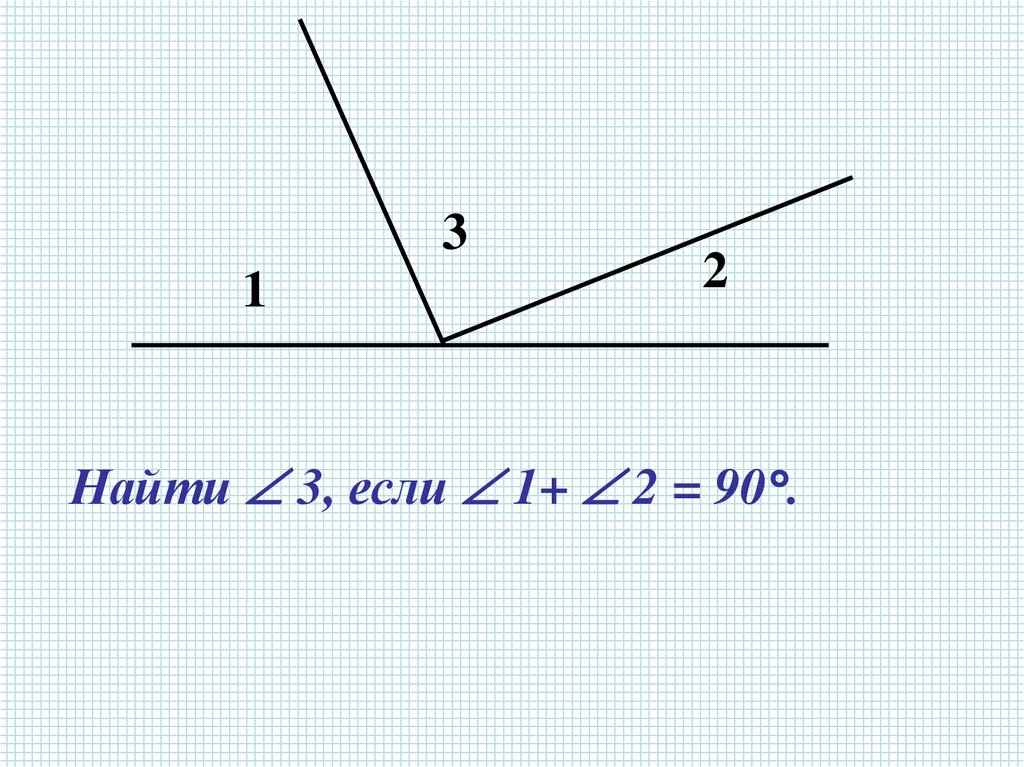
Найти 3, если 1+ 2 = 90°.
7.
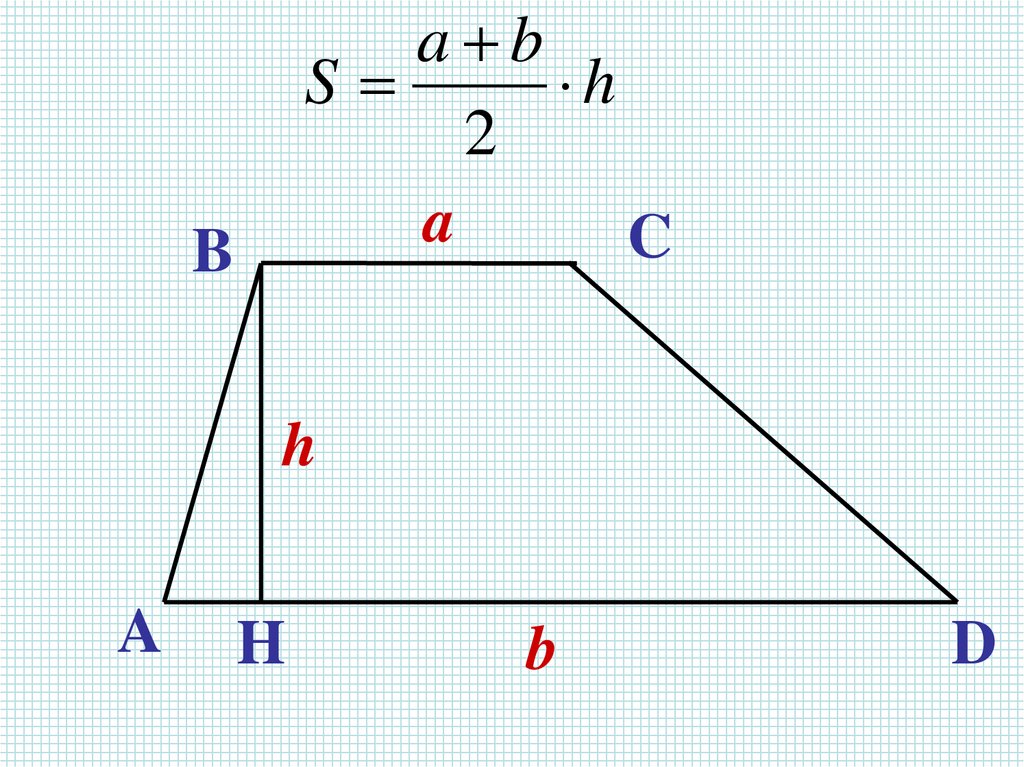
a bS
h
2
a
C
B
h
A
H
b
D
8.
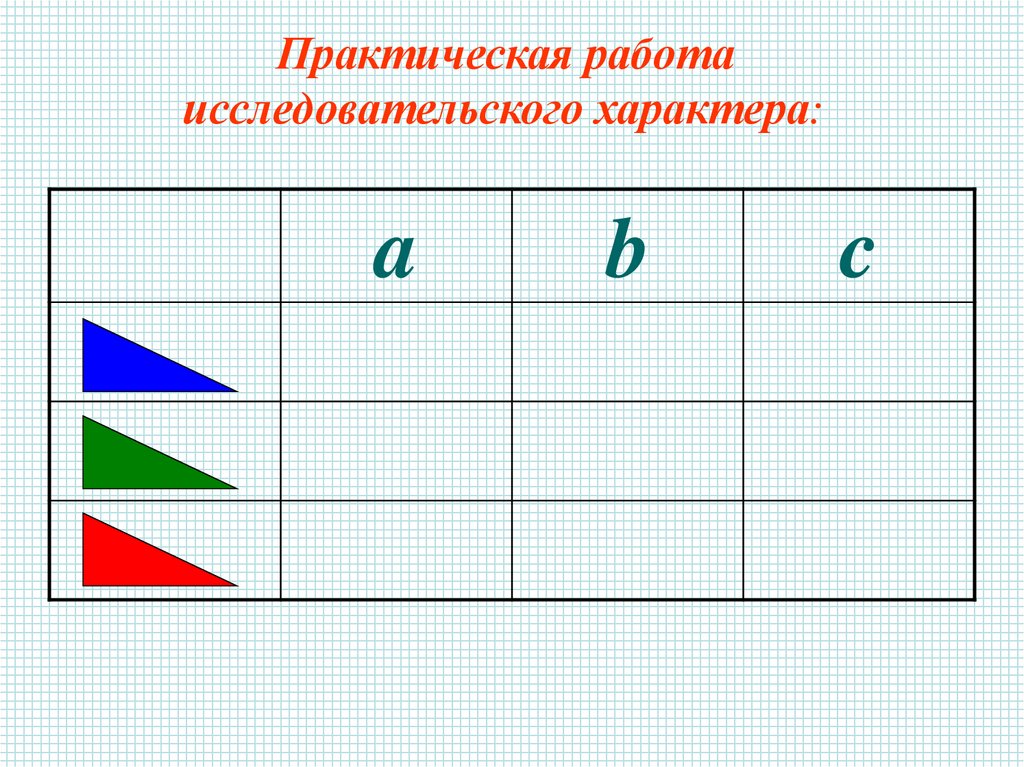
Практическая работаисследовательского характера:
a
b
c
9.
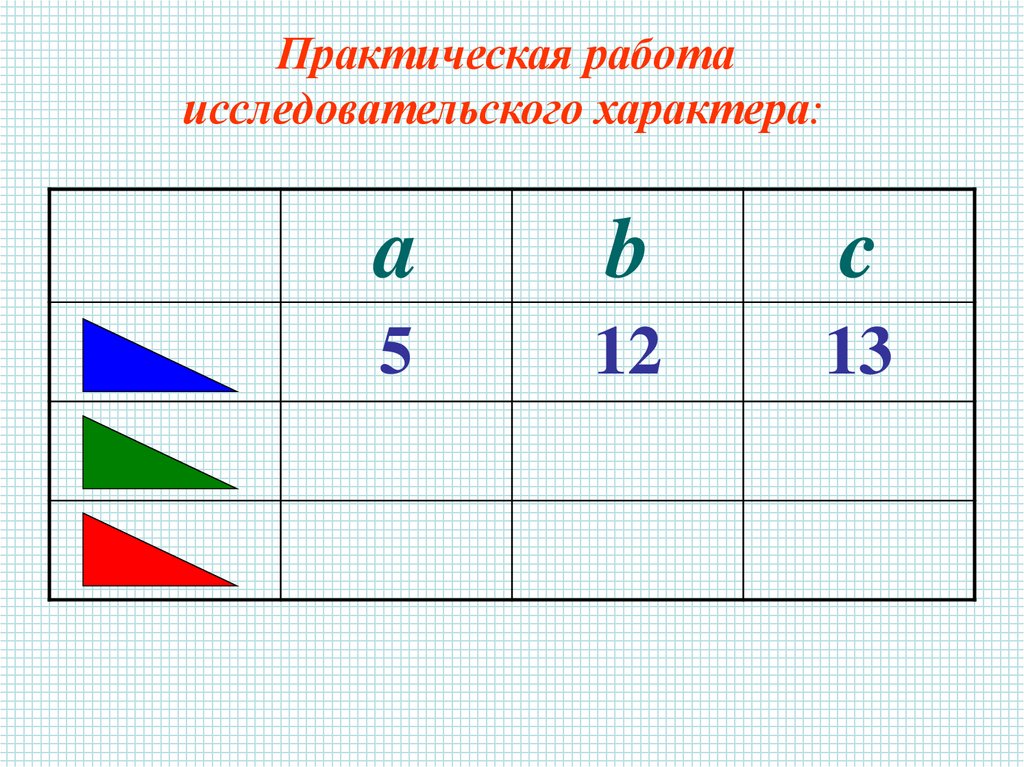
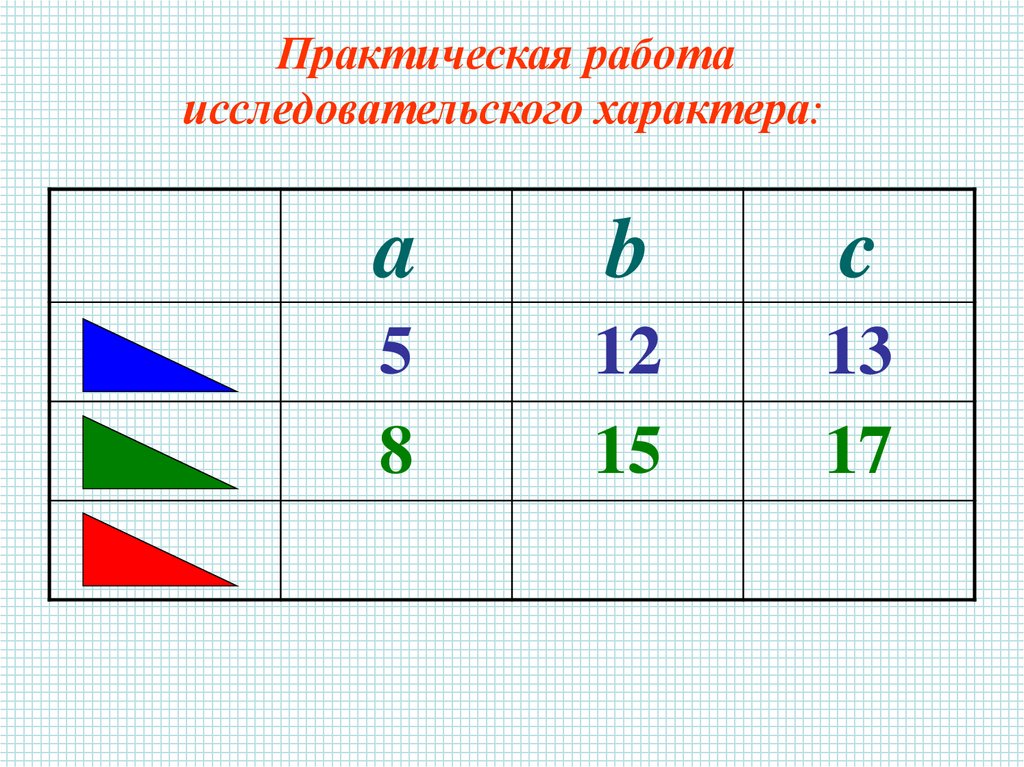
Практическая работаисследовательского характера:
a
b
c
5
12
13
10.
Практическая работаисследовательского характера:
a
b
c
5
8
12
15
13
17
11.
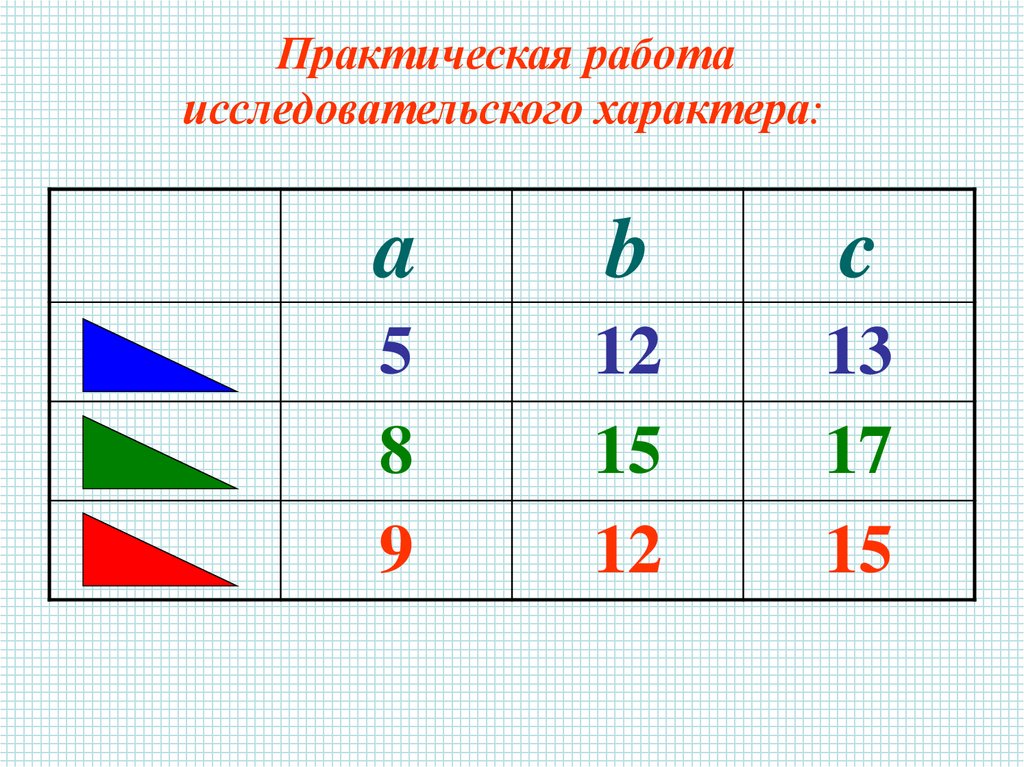
Практическая работаисследовательского характера:
a
b
c
5
8
9
12
15
12
13
17
15
12.
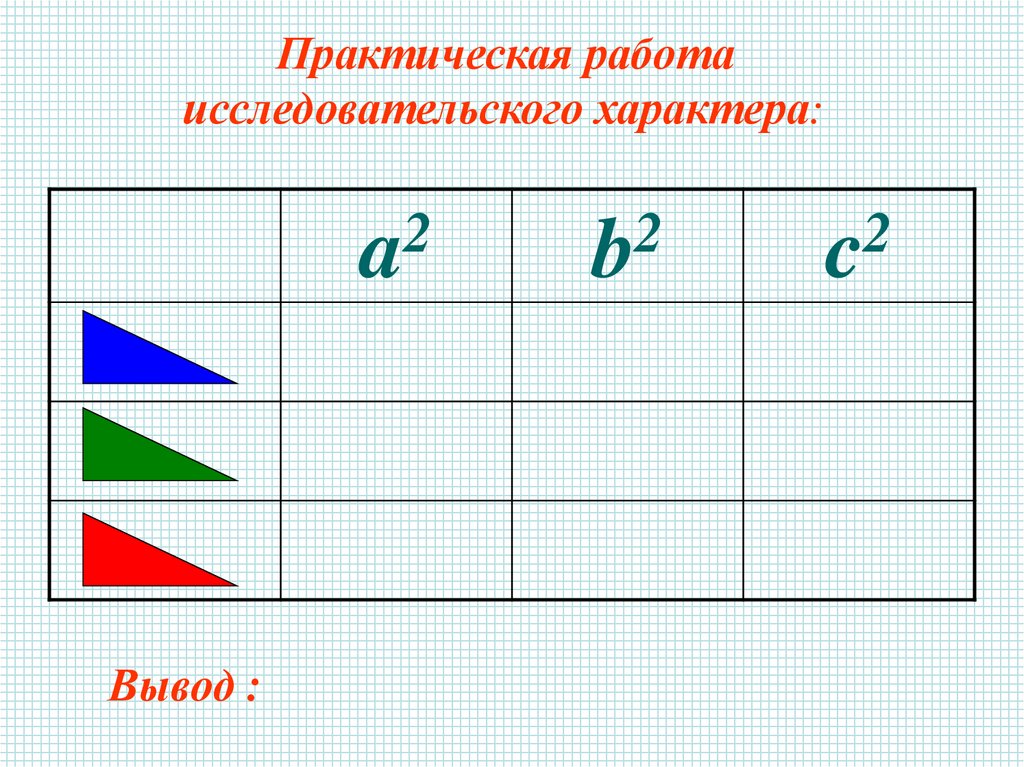
Практическая работаисследовательского характера:
2
a
Вывод :
2
b
2
c
13.
Практическая работаисследовательского характера:
Вывод :
2
a
2
b
2
c
25
144
169
14.
Практическая работаисследовательского характера:
Вывод :
2
a
2
b
2
c
25
64
144
225
169
289
15.
Практическая работаисследовательского характера:
Вывод :
2
a
2
b
2
c
25
64
81
144
225
144
169
289
225
2
c
=
2
a
+
2
b
16.
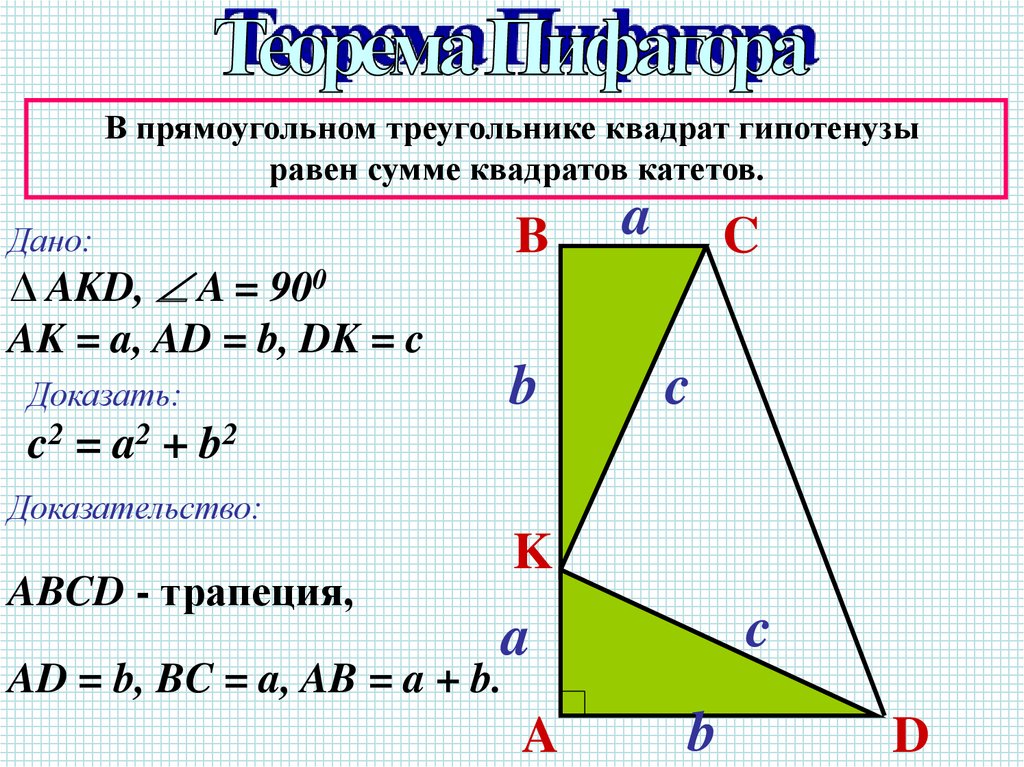
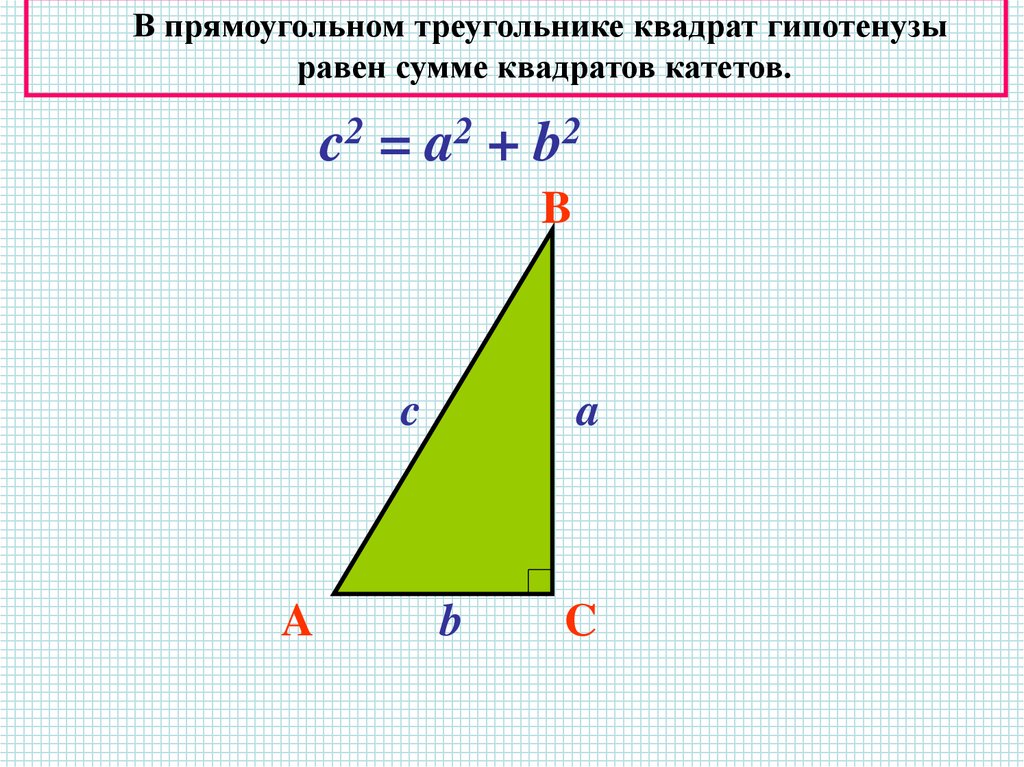
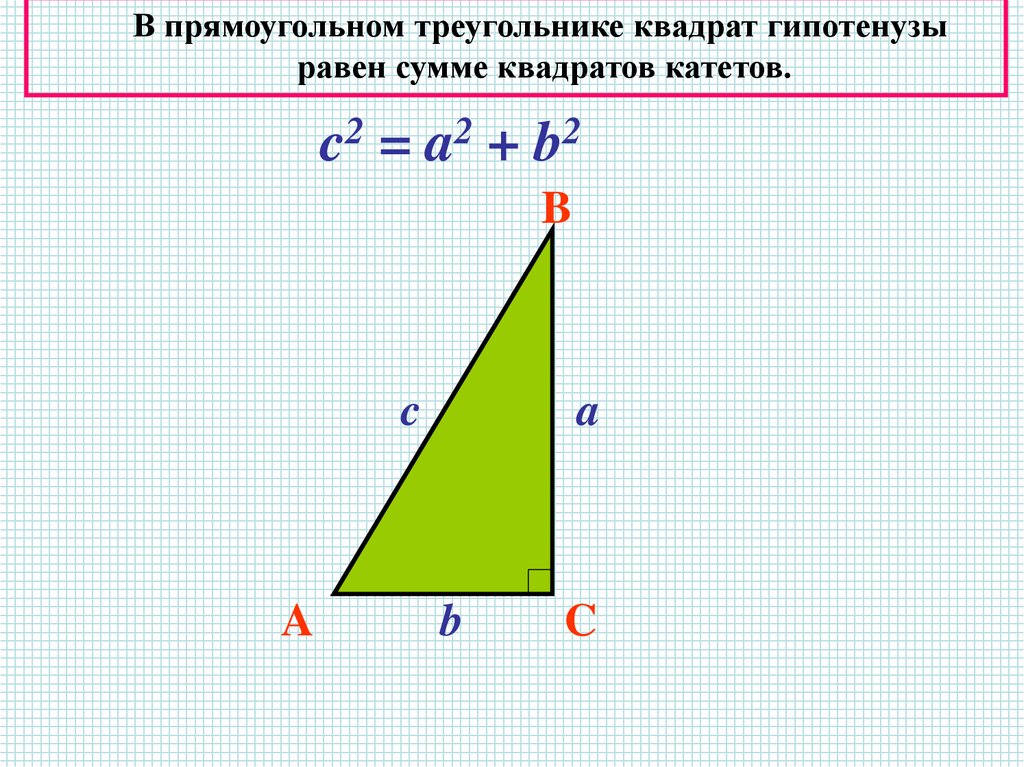
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов.
B
Дано:
∆ AKD, A = 900
AK = a, AD = b, DK = c
b
Доказать:
a
C
c
c2 = a2 + b 2
Доказательство:
K
ABCD - трапеция,
c
a
AD = b, BC = a, AB = a + b.
A
b
D
17.
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов.
c2 = a 2 + b 2
B
c
A
a
b
C
18.
19.
20.
21.
22.
23.
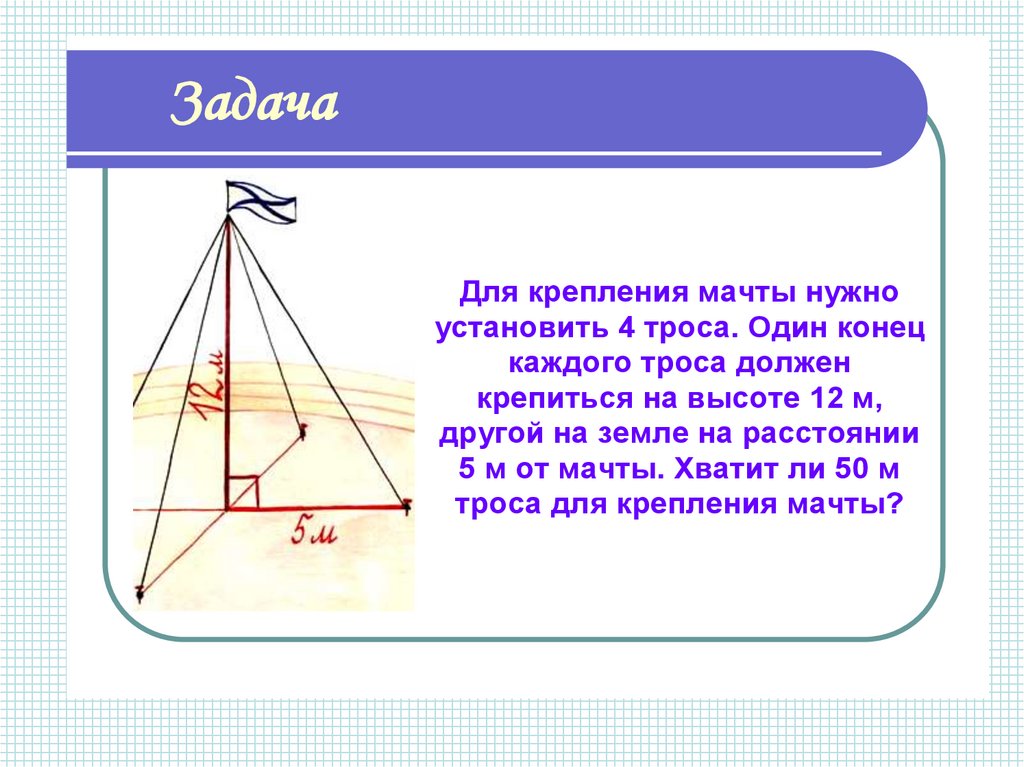
ЗадачаДля крепления мачты нужно
установить 4 троса. Один конец
каждого троса должен
крепиться на высоте 12 м,
другой на земле на расстоянии
5 м от мачты. Хватит ли 50 м
троса для крепления мачты?
24.
2c
=
2
a
B
2
c
c
a
b
A
C
2
b
2
a
+
2
b
25.
Aа
6
5
b
8
c
b
c
61
8 3
16
C
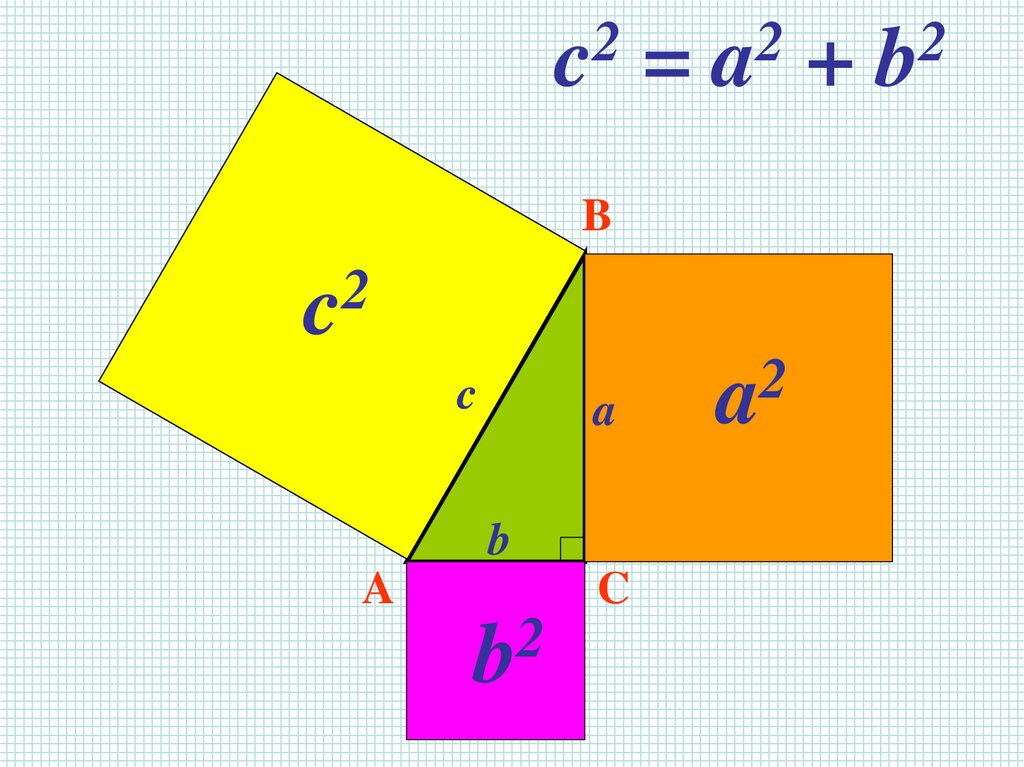
с² = а² + b²
c2 =
c2 =
c=
с² = а² + b²
b² =
b² =
b=
a
с² = а² + b²
a² =
a² =
a=
B
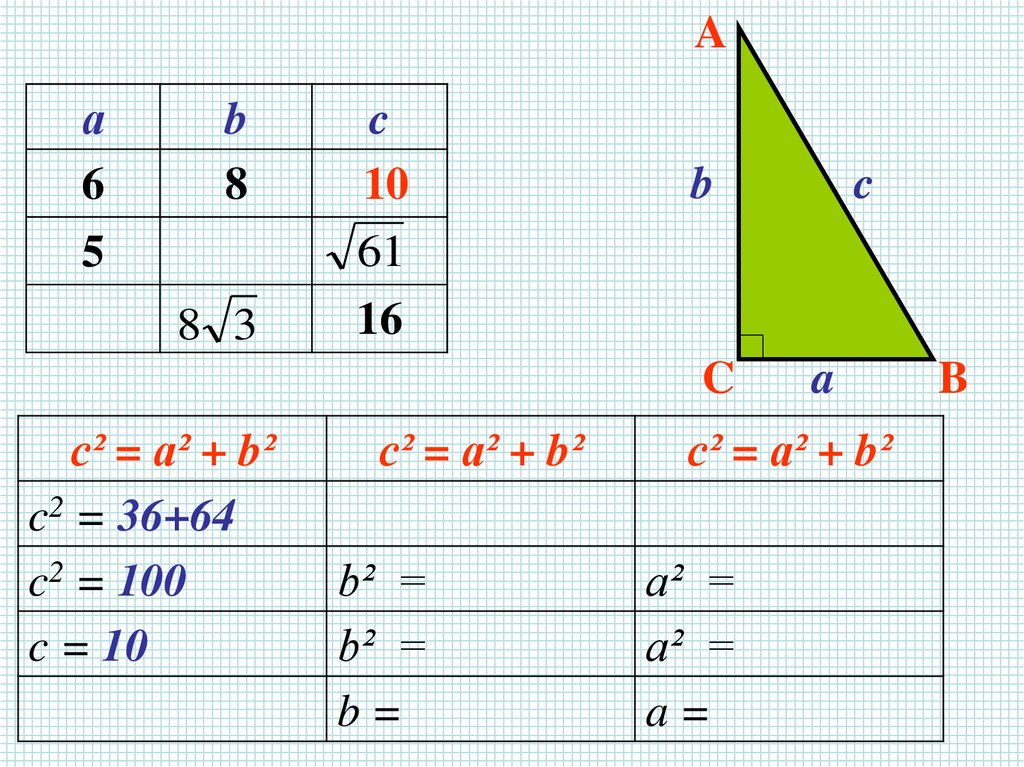
26.
Aа
6
5
b
8
8 3
c
10
61
16
b
C
с² = а² + b²
c2 = 36+64
c2 = 100
c = 10
с² = а² + b²
b² =
b² =
b=
c
a
с² = а² + b²
a² =
a² =
a=
B
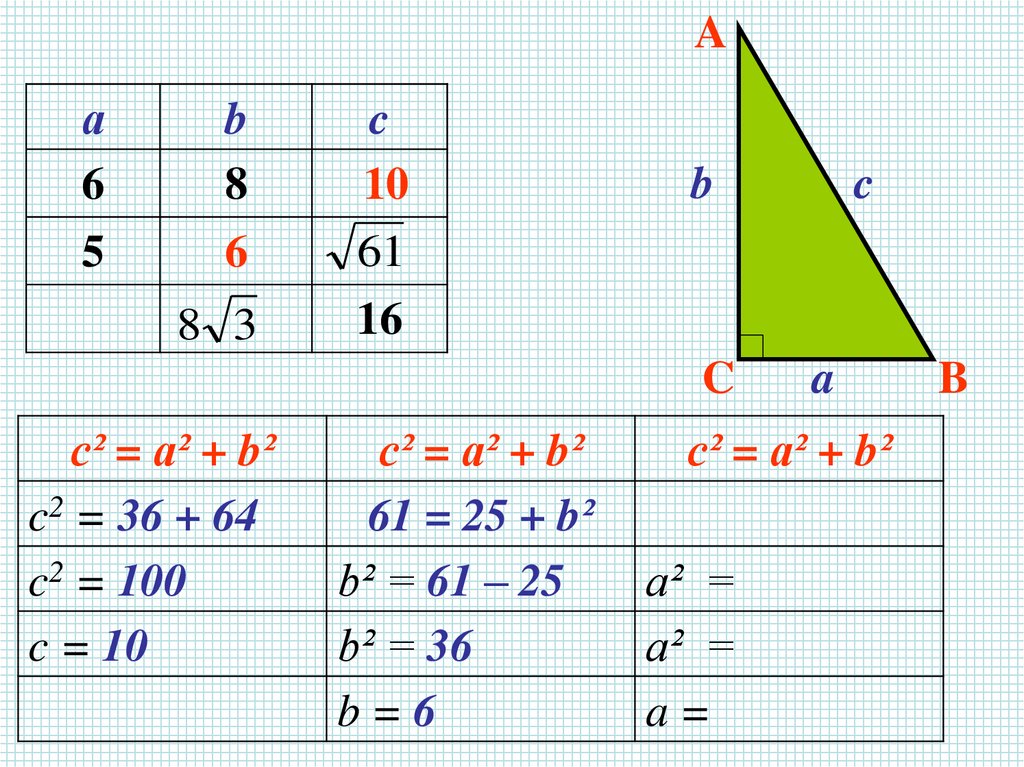
27.
Aа
6
5
b
8
6
8 3
c
10
61
16
b
C
с² = а² + b²
c2 = 36 + 64
c2 = 100
c = 10
с² = а² + b²
61 = 25 + b²
b² = 61 – 25
b² = 36
b=6
c
a
с² = а² + b²
a² =
a² =
a=
B
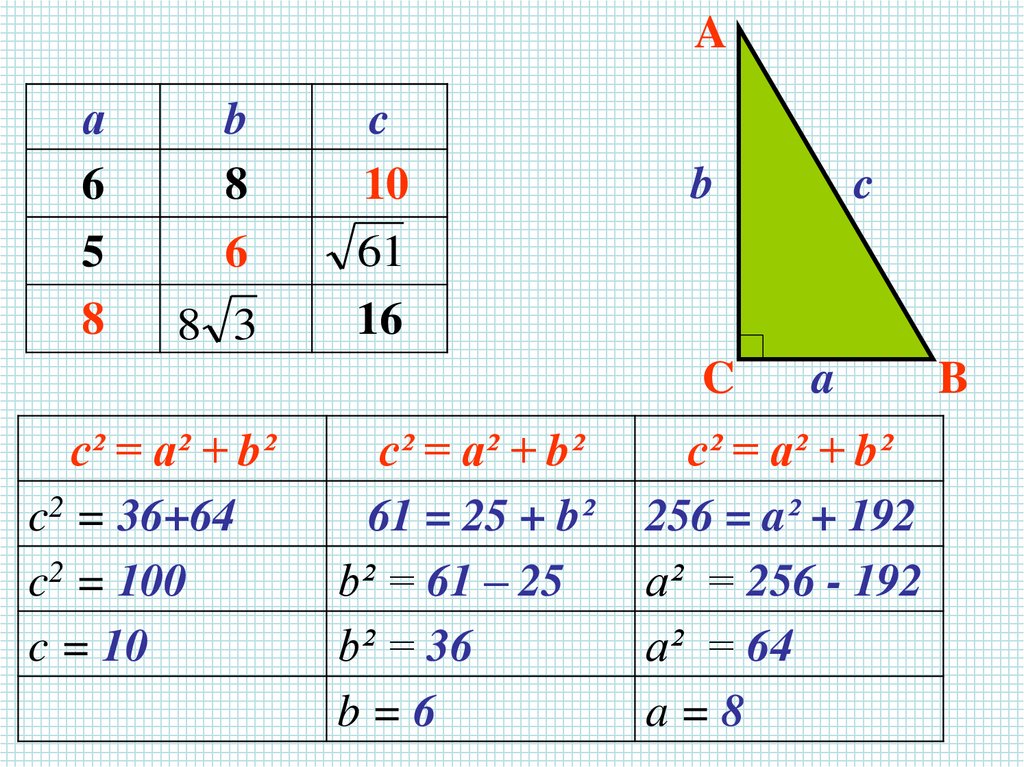
28.
Aа
6
5
8
b
8
6
8 3
c
10
61
16
b
C
с² = а² + b²
c2 = 36+64
c2 = 100
c = 10
с² = а² + b²
61 = 25 + b²
b² = 61 – 25
b² = 36
b=6
c
a
с² = а² + b²
256 = a² + 192
a² = 256 - 192
a² = 64
a=8
B
29.
Задание ОГЭ и ЕГЭ30.
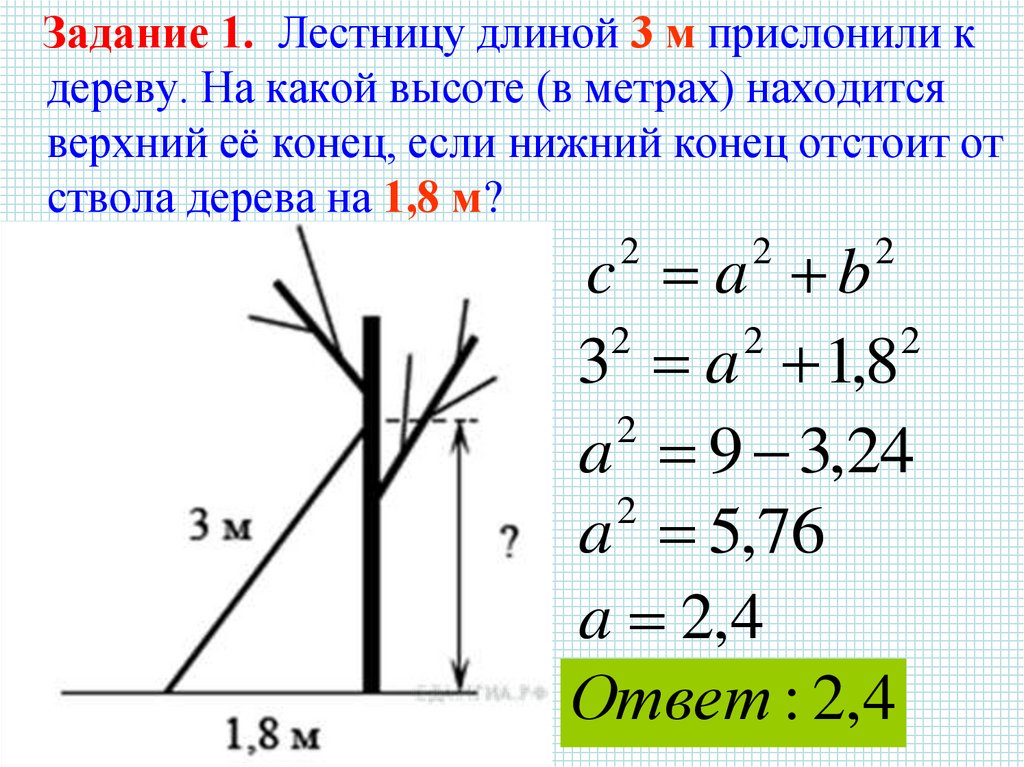
Задание 1. Лестницу длиной 3 м прислонили кдереву. На какой высоте (в метрах) находится
верхний её конец, если нижний конец отстоит от
ствола дерева на 1,8 м?
c a b
2
2
2
3 a 1,8
2
a 9 3,24
2
a 5,76
a 2,4
Ответ : 2,4
2
2
2
31.
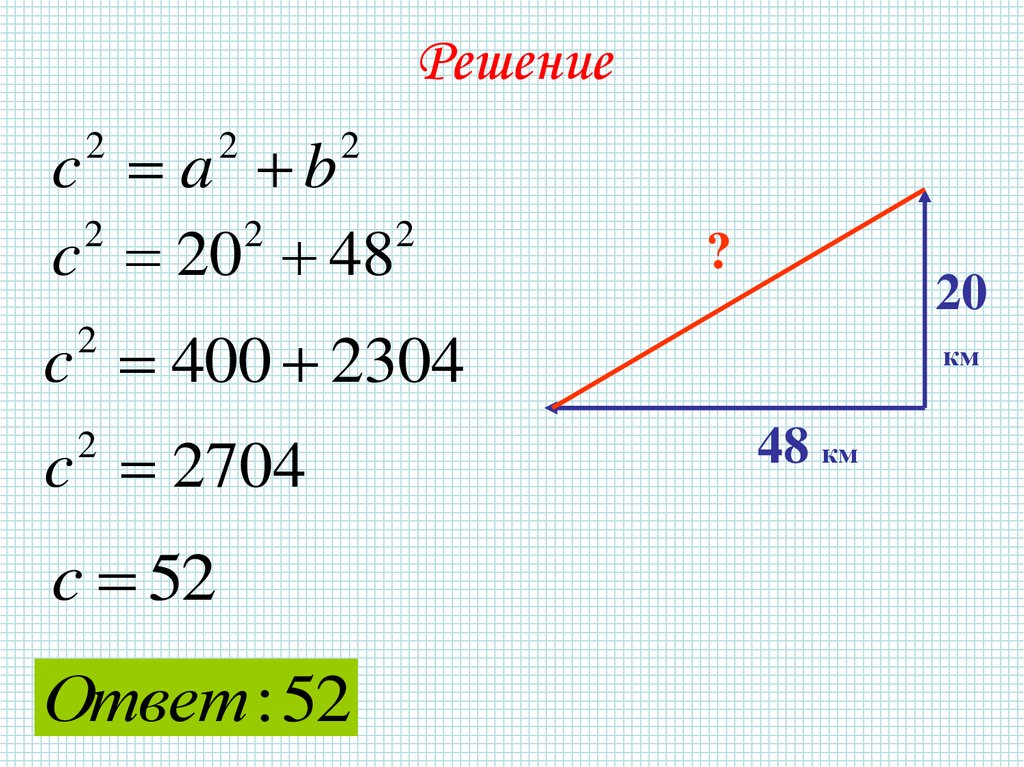
Задание 2. Два теплохода вышли из порта, следуя одинна север, другой на запад. Скорости их равны
соответственно 10 км/ч и 24 км/ч. Какое расстояние
(в километрах) будет между ними через 2 часа?
32. Решение
c a b2
2
2
c 20 48
2
2
2
?
20
c 400 2304
2
c 2704
2
c 52
Ответ : 52
км
48 км
33.
В прямоугольном треугольнике квадрат гипотенузыравен сумме квадратов катетов.
c2 = a 2 + b 2
B
c
A
a
b
C
34.
54
3
8
4
5
6
35.
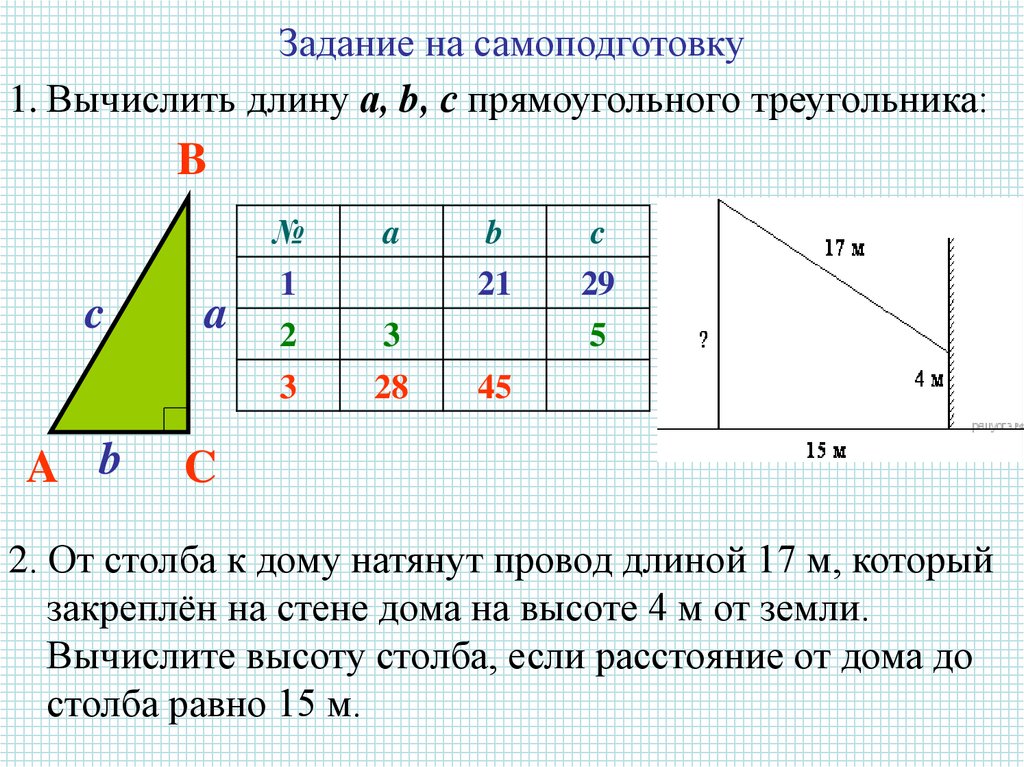
Задание на самоподготовку1. Вычислить длину а, b, с прямоугольного треугольника:
B
c
a
№
1
2
3
A b
a
3
28
b
21
c
29
5
45
C
2. От столба к дому натянут провод длиной 17 м, который
закреплён на стене дома на высоте 4 м от земли.
Вычислите высоту столба, если расстояние от дома до
столба равно 15 м.
36.
На обоих берегах реки растет по дереву, одна против другой.Высота одной 30 метров, другой -20 метров. Расстояние между их
основаниями - 50 метров.
На верхушке каждого дерева сидит птица. Внезапно обе птицы
заметили рыбу, выплывшую к поверхности воды между деревьями.
Они кинулись к ней разом и достигли её одновременно. На каком
расстоянии от основания более высокого дерева появилась рыба?














 mathematics
mathematics