Similar presentations:
Тест по теме: "Цилиндр, конус, шар, поверхности и объемы тел"
1. МКОУ «Погорельская СОШ» Кощеев М.М.
Вариант 1Вариант 2
Использован шаблон создания тестов в PowerPoint
2. Результат теста
Верно: 13Ошибки: 0
Отметка: 5
Время: 0 мин. 28 сек.
ещё
3. Вариант 1
1. Цилиндром называется тело,ограниченное поверхностью:
а) конической
б) концентрической
в) цилиндрической
г) сферическо
3
4. Вариант 1
2. Назовите элемент, не принадлежащийцилиндру.
а) апофема
б) высота
в) образующая
г) радиус
4
5. Вариант 1
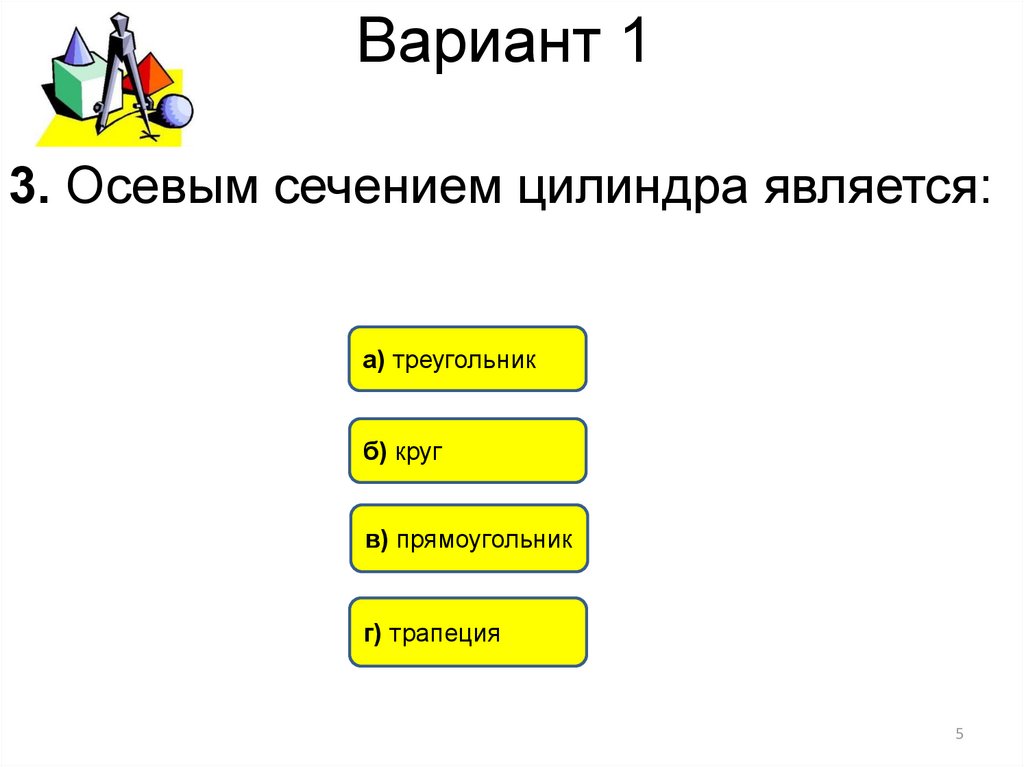
3. Осевым сечением цилиндра является:а) треугольник
б) круг
в) прямоугольник
г) трапеция
5
6. Вариант 1
4. Боковая поверхность цилиндраопределяется по формуле, где Lобразующая, R- радиус, Н-высота:
а) 2ПRL
б) ПR²H
в) ПRН
г) ПRL
6
7. Вариант 1
5. Полная поверхность цилиндраопределяется по формуле, где R-радиус
основания, L- образующая, Н- высота:
а)
2ПR(R+H)
б)
2ПL(L+H)
в)
2ПR²+2ПRL²
г)
ПRL²+ПRН
7
8. Вариант 1
6. Конус может быть получен вращением:а) прямоугольника вокруг одной из его сторон
б) равностороннего треугольника вокруг медианы
в) прямоугольного треугольника вокруг одного из его катетов
г) равнобедренного треугольника
8
9. Вариант 1
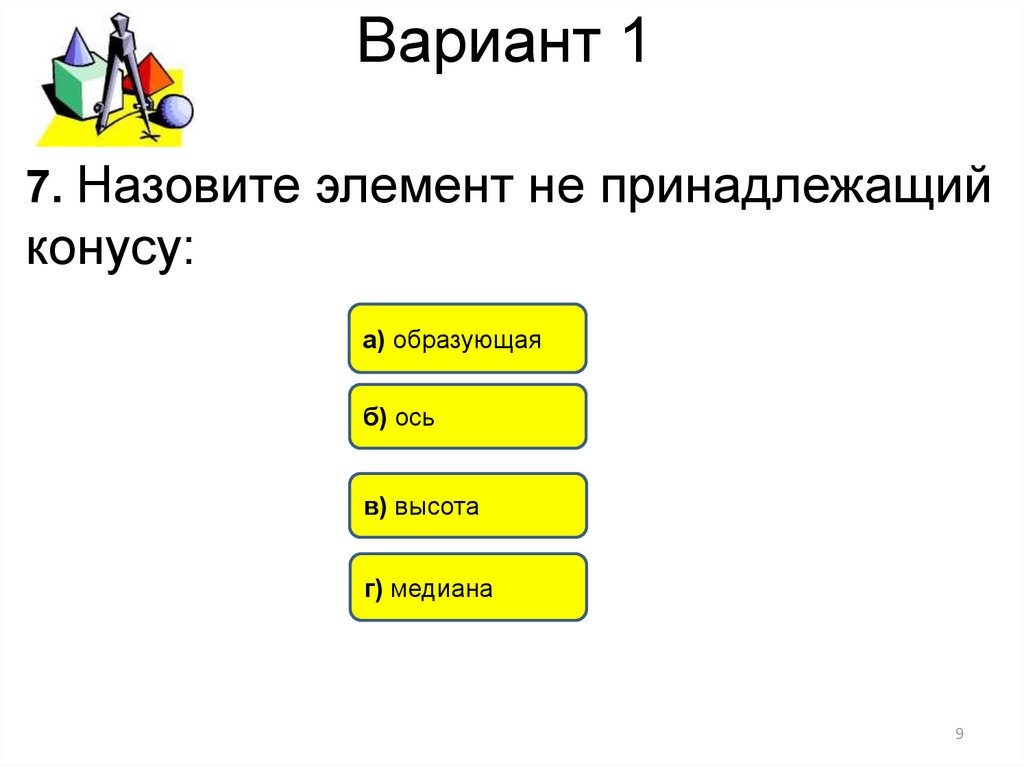
7. Назовите элемент не принадлежащийконусу:
а) образующая
б) ось
в) высота
г) медиана
9
10. Вариант 1
8. Выявите формулу, не относящуюся квычислению площади поверхности или
объема конуса, где L- образующая, Rрадиус, Н-высота.
а)
ПRL
б)
ПRН
в)
ПR(L+R)
г)
⅓ПR²Н
10
11. Вариант 1
9. Боковой поверхностью усеченногоконуса является:
а) Часть цилиндрической поверхности
б) Часть сферической поверхности
в) Часть поверхности шара
г) Часть конической поверхности
11
12. Вариант 1
10. Площадь боковой поверхностиусеченного конуса определяется по
формуле, где R и R₁ – радиусы
основания усеченного конуса, Нвысота:
a)
П(R²+R₁²)L
б)
П(R+R₁)L
в)
ПRL+П(R-R₁)L
г)
ПRH+ПR₁Н
12
13. Вариант 1
11. Апофема – это …..а) образующая цилиндра
б) высота конуса
в) высота боковой грани пирамиды
г) высота усеченного конуса
13
14. Вариант 1
12. Если высота конуса 15см, а радиусоснования 8см, образующая конуса
равна:
а)
14 см
б)
17 см
в)
13 см
г)
6 см
14
15. Вариант 1
13. Шар и цилиндр имеют равныеобъемы, а диаметр шара равен
диаметру основания цилиндра. Если
выразить высоту цилиндра через радиус
шара, то она будет равна:
а)
√Rшара
б)
Rшара
в)
1/3Rшара
г)
4/3Rшара
15
16. Вариант 2
1. Сфера является поверхностью:а) конуса
б) усеченного конуса
в) цилиндра
г) шара
16
17. Вариант 2
2. Выявите уравнение которое неявляется уравнением сферы:
а) (х-1)²+(у-2)²+(z-3)²=16
б) (х-1)²+у²+z²=25
в) х²+(у-1)+(z-1)²=4
г) х²+у²+(z-2)²=7
17
18. Вариант 2
3. Сфера и плоскость не могут иметь:а) одну общую точку
б) ни одной общей точки
в) две общие точки
г) много общих точек
18
19. Вариант 2
4. Площадь поверхности сферыопределяется по формуле, где R-радиус
сферы:
a)
2ПR²
б)
4ПR³
в)
4П²R²
г)
4ПR²
19
20. Вариант 2
5. Какой не может быть призма?а) прямой
б) наклонной
в) правильной
г) усеченной
20
21. Вариант 2
6. Какая формула используется длявычисления как объема призмы, так и
цилиндра, где R-радиус основания,
Н-высота?
а)
⅓Sосн∙Н
б)
ПR²Н
в)
Sосн∙ Н
г)
⅓Н(S+S₁+√SS₁
21
22. Вариант 2
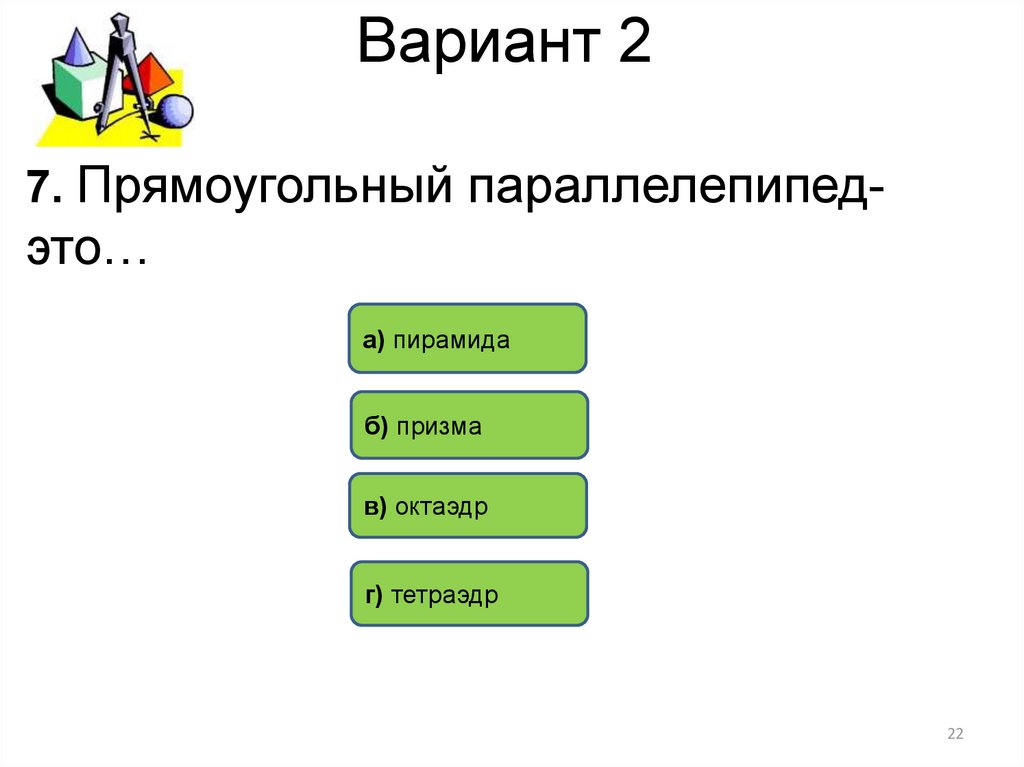
7. Прямоугольный параллелепипед-это…
а) пирамида
б) призма
в) октаэдр
г) тетраэдр
22
23. Вариант 2
8. Назовите, какая фигура не являетсяправильным многогранником:
а) куб
б) додекаэдр
в) октаэдр
г)параллелепипед
23
24. Вариант 2
9. Объем пирамиды определяется поформуле, где Sосн- площадь основания,
Н- высота, R- радиус
а)
⅓∙Sосн∙ Н
б)
⅓ПR²Н
в)
Sосн∙Н
г)
⅔ПR²Н
24
25. Вариант 2
10. Объем конуса определяется поформуле, где Sосн- площадь основания,
Н- высота, R- радиус:
а)
⅓∙ПR²∙ Н
б)
ПR²Н
в)
Sосн∙Н
г)
4/3ПR³
25
26. Вариант 2
11. Определите формулу, не имеющуюотношения к определению объема шара
и его частей (сегмент, слой, сектор), где
R- радиус, Н- высота:
a)
4/3ПR³
б)
ПН²(R-⅓∙Н)
в)
⅔∙ПR²Н
г)
4ПR²
26
27. Вариант 2
12. Объем правильной треугольнойпирамиды, высота которой равна 12см, а
сторона основания 13см, равняется:
а)
156 см³
б)
207 см³
в)
169√3 см³
г)
24√6 см³
27
28. Вариант 2
13. Шар и цилиндр имеют равныеобъемы, а диаметр шара равен
диаметру основания цилиндра. Если
выразить высоту цилиндра через радиус
шара, то она будет равна:
а)
√Rшара
б)
Rшара
в)
1/3Rшара
г)
4/3Rшара
28
29.
Ключи к тесту: Цилиндр, конус, шар. Поверхности и объемы тел1вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
Отв.
в
а
в
а
а
в
г
б
г
б
в
б
г
2вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
Отв.
г
в
в
г
г
в
б
г
а
а
г
в
г
Литература
Ю.А. Киселева. Геометрия 9-11 классы. Обобщающее повторение. Изд-во «Учитель», 2009г.
29


























 mathematics
mathematics








