Тест по теме: «Перпендикулярные прямые в пространстве. Перпендикулярность прямой и плоскости»

1. МКОУ «Погорельская СОШ» Кощеев М.М.

Тест по теме:
«Перпендикулярные
прямые в пространстве.
Перпендикулярность
прямой и плоскости»
Вариант 1
Вариант 2
Использован шаблон создания тестов в PowerPoint

2. Результат теста

Верно: 14
Ошибки: 0
Отметка: 5
Время: 2 мин. 51 сек.
ещё

3. Вариант 1

1. Какое утверждение верно?
а) Если одна из двух прямых перпендикулярна к третьей прямой,
то и другая прямая перпендикулярна к этой прямой.
б) Если две прямые перпендикулярны к третье прямой, то они
параллельны.
в) Если две прямые перпендикулярны к плоскости, то они
параллельны.
3

4. Вариант 1

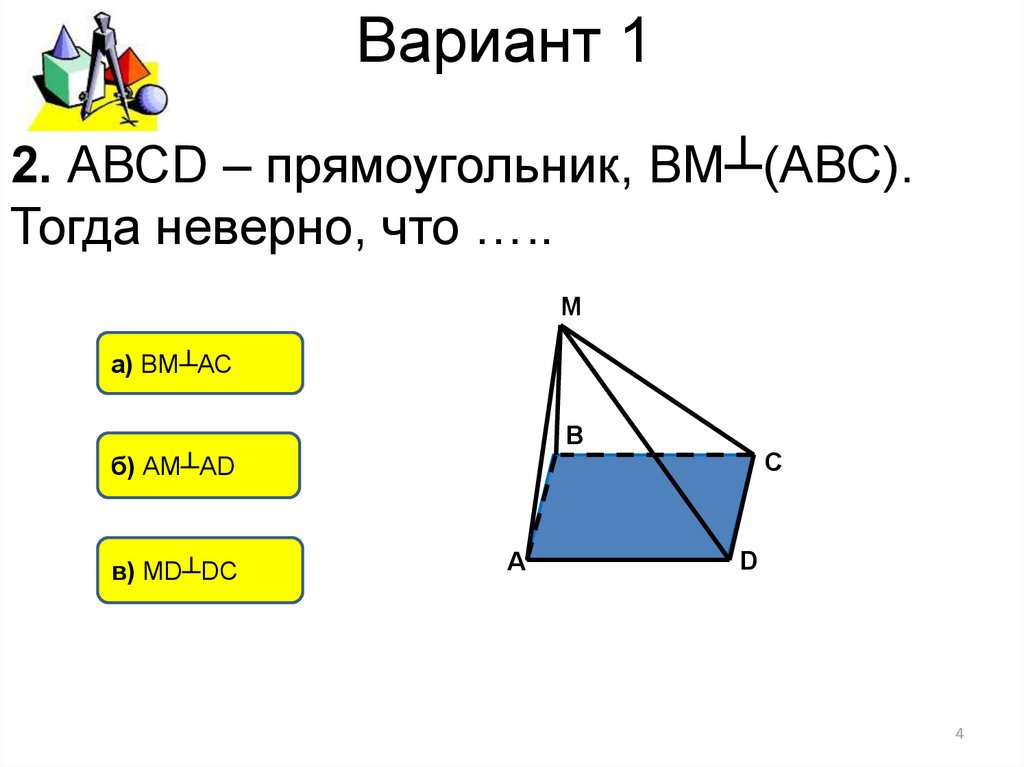
2. АВСD – прямоугольник, ВМ┴(АВС).
Тогда неверно, что …..
М
а) ВМ┴АС
В
С
б) АМ┴АD
в) MD┴DC
А
D
4

5. Вариант 1

3. Прямая m перпендикулярна к прямым
а и b, лежащим в плоскости α, но m не
перпендикулярна к плоскости α. Тогда
прямые а и b …..
а) Параллельны
б) Пересекаются.
в) Скрещиваются
5

6. Вариант 1

4. Плоскость α проходит через
вершину А ромба АВСD
перпендикулярно диагонали АС. Тогда
диагональ ВD…..
а) перпендикулярна плоскости α
б) параллельна плоскости α
в) лежит в плоскости α
6

7. Вариант 1

5. а║α b┴α. Тогда прямые а и b не
могут быть…..
а) скрещивающимися
б) перпендикулярными
в) параллельными
7

8. Вариант 1

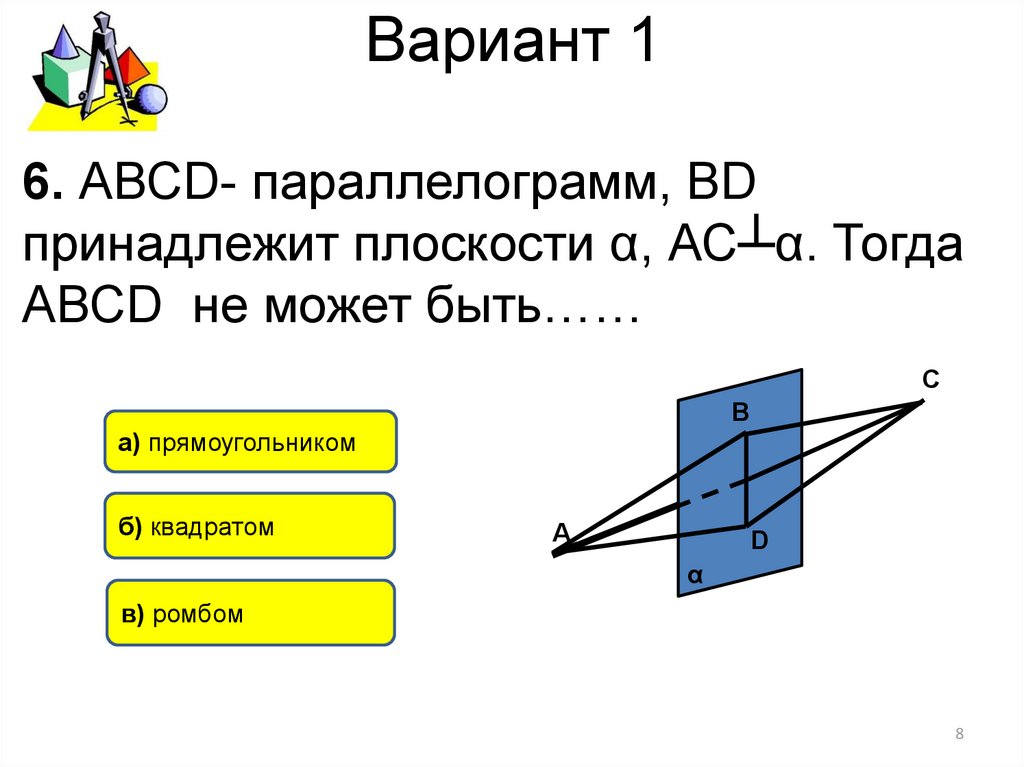
6. АВСD- параллелограмм, ВD
принадлежит плоскости α, АС┴α. Тогда
АВСD не может быть……
С
В
а) прямоугольником
б) квадратом
А
D
α
в) ромбом
8

9. Вариант 1

7. Прямая перпендикулярна плоскости
круга, если она перпендикулярна двум…
а) радиусам
б) диаметрам
в) хордам
9

10. Вариант 1

8. Какое утверждение верное?
а) Прямая и не проходящая через нее плоскость, перпендикулярные
другой плоскости, параллельны между собой.
б) Плоскость, перпендикулярная данной плоскости, перпендикулярна и
к прямой , параллельной данной плоскости
в) Плоскость, перпендикулярная данной прямой, перпендикулярна и к
плоскости, параллельной данной прямой
10

11. Вариант 1

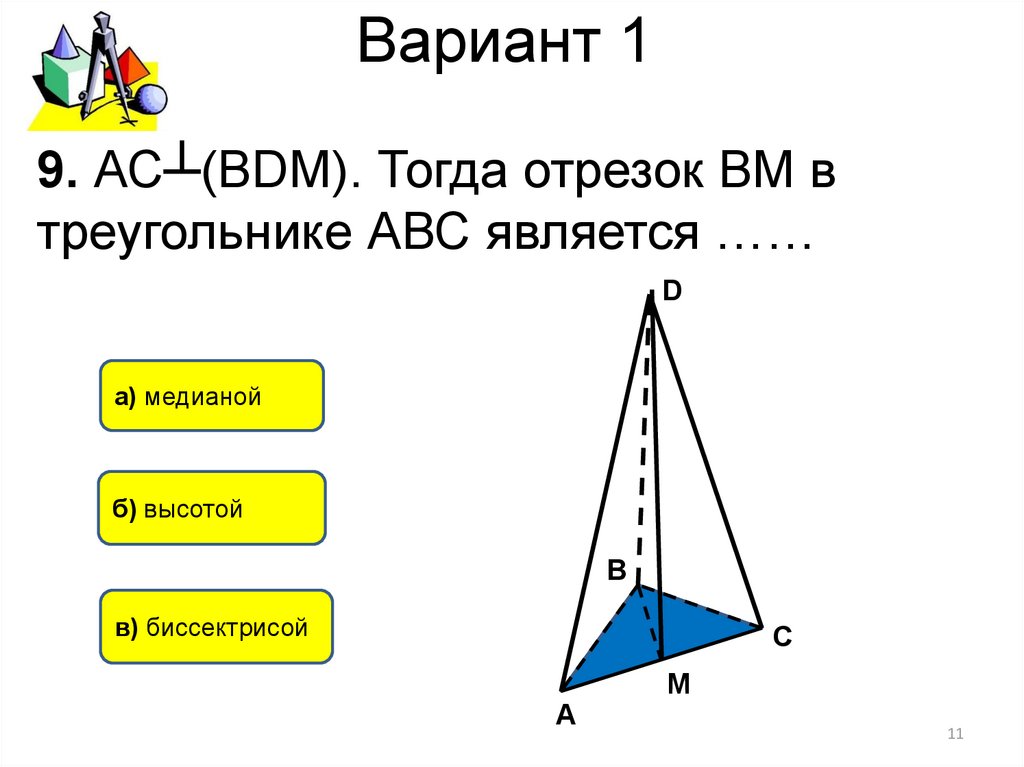
9. АС┴(ВDМ). Тогда отрезок ВМ в
треугольнике АВС является ……
D
а) медианой
б) высотой
В
в) биссектрисой
С
А
М
11

12. Вариант 1

10. а┴(АВС). ВМ- медиана треугольника
АВС. Тогда <(а, ВМ) равен…..
а
а) 90°
б) 60°
в) 45°
А
М
С
В
12

13. Вариант 1

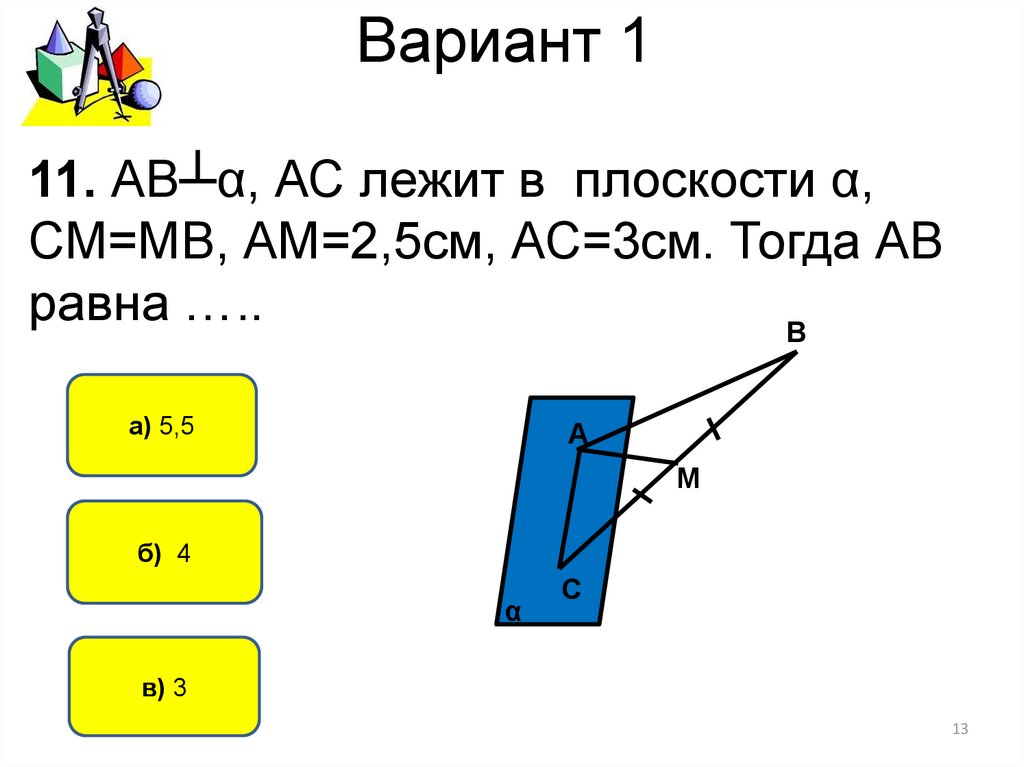
11. АВ┴α, АС лежит в плоскости α,
СМ=МВ, АМ=2,5см, АС=3см. Тогда АВ
равна …..
В
а) 5,5
А
М
б) 4
α
С
в) 3
13

14. Вариант 1

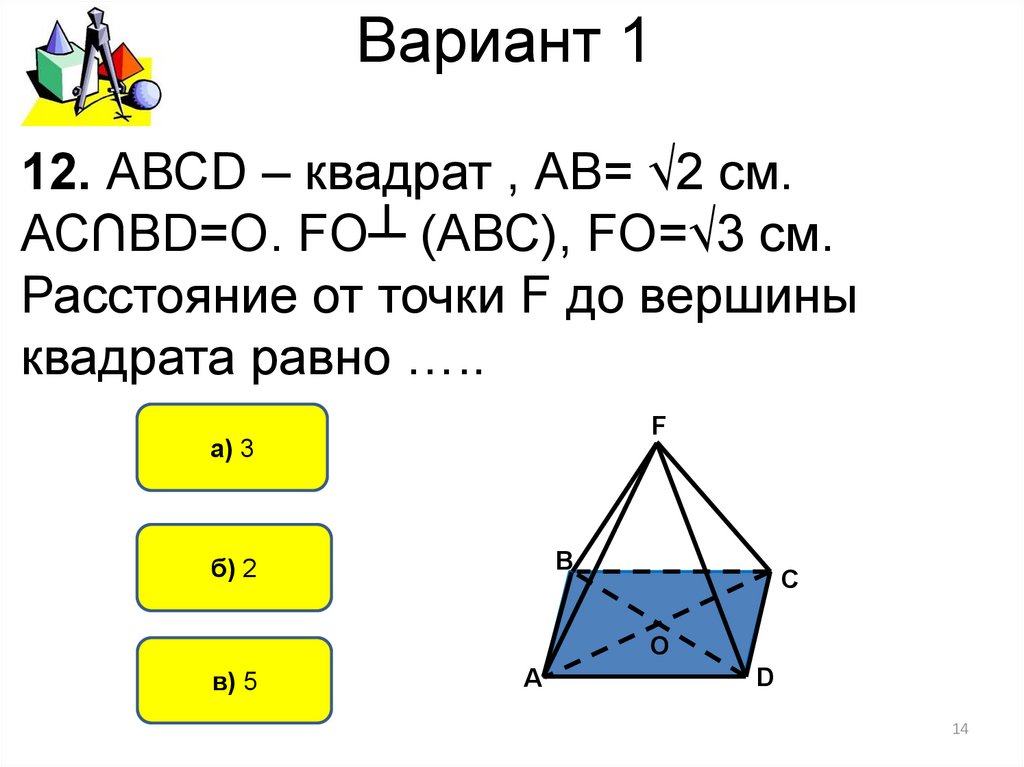
12. АВСD – квадрат , АВ= √2 см.
АС∩ВD=O. FO┴ (АВС), FO=√3 см.
Расстояние от точки F до вершины
квадрата равно …..
F
а) 3
В
б) 2
С
О
в) 5
А
D
14

15. Вариант 1

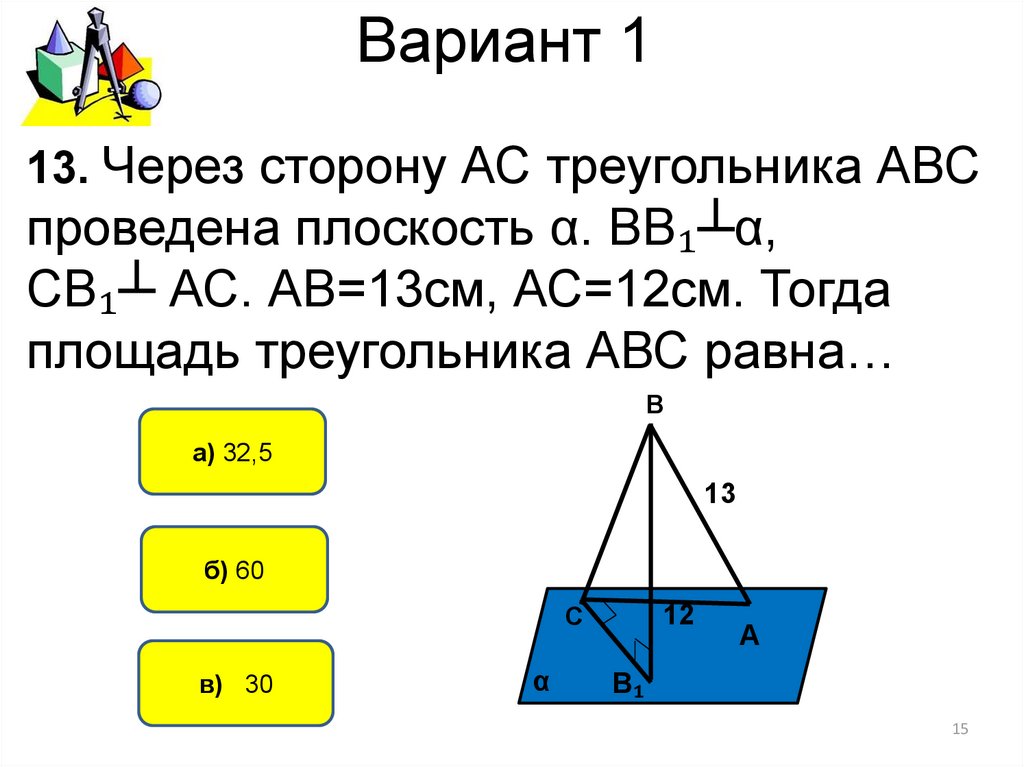
13. Через сторону АС треугольника АВС
проведена плоскость α. ВВ₁┴α,
СВ₁┴ АС. АВ=13см, АС=12см. Тогда
площадь треугольника АВС равна…
В
а) 32,5
13
б) 60
С
в) 30
α
12
А
В₁
15

16. Вариант 1

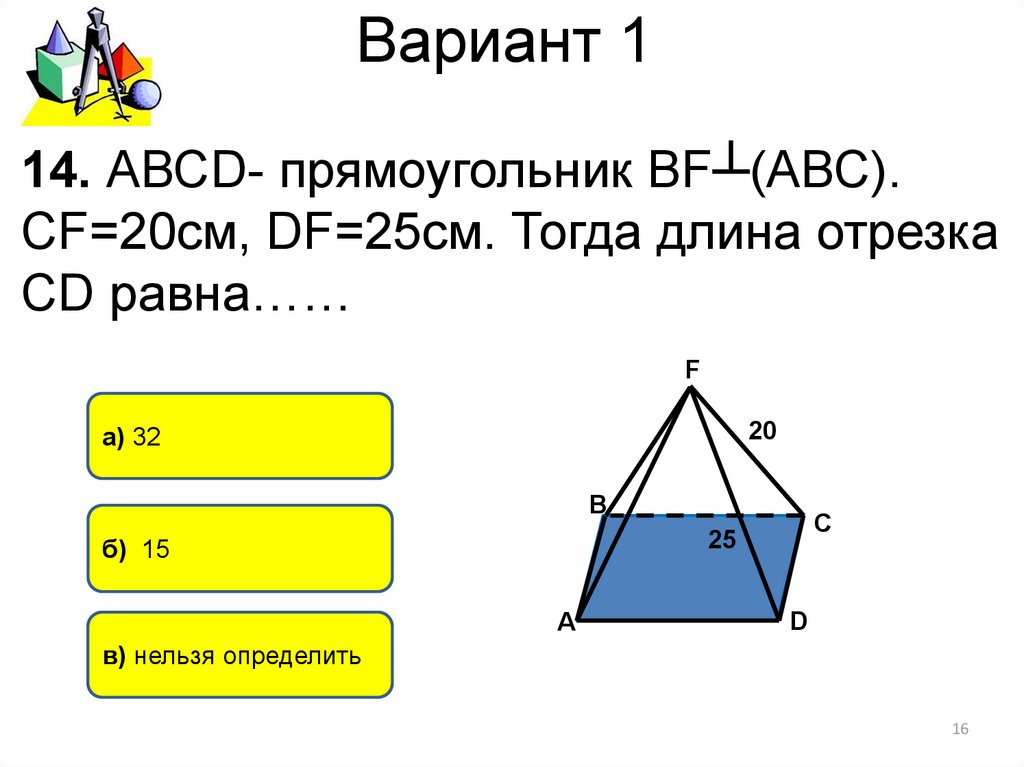
14. АВСD- прямоугольник ВF┴(АВС).
СF=20см, DF=25см. Тогда длина отрезка
СD равна……
F
20
а) 32
В
С
25
б) 15
А
D
в) нельзя определить
16

17. Вариант 2

1. Прямая называется перпендикулярной
к плоскости, если она перпендикулярна…
а) К одной прямой , лежащей в плоскости
б) К двум прямым, лежащим в этой плоскости
в) К любой прямой, лежащей в этой плоскости
17

18. Вариант 2

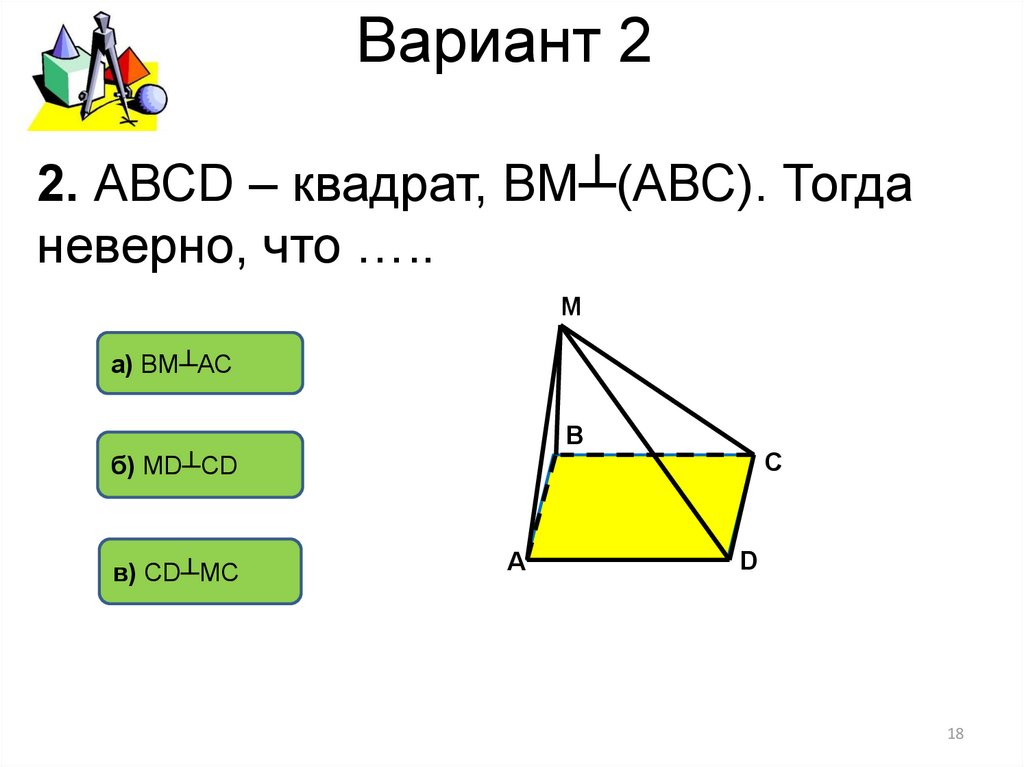
2. АВСD – квадрат, ВМ┴(АВС). Тогда
неверно, что …..
М
а) ВМ┴АС
В
С
б) МD┴CD
в) СD┴МC
А
D
18

19. Вариант 2

3. а┴α, прямая b не перпендикулярна
плоскости α. Тогда прямые а и b не
могут быть…..
а) Перпендикулярными
б) Параллельными
в) Скрещивающимися
19

20. Вариант 2

4. Диагональ АС квадрата АВСD
перпендикулярна некоторой
плоскости α, проходящей через точку
А. Тогда диагональ ВD…..
а) перпендикулярна плоскости α
б) параллельна плоскости α
в) лежит в плоскости α
20

21. Вариант 2

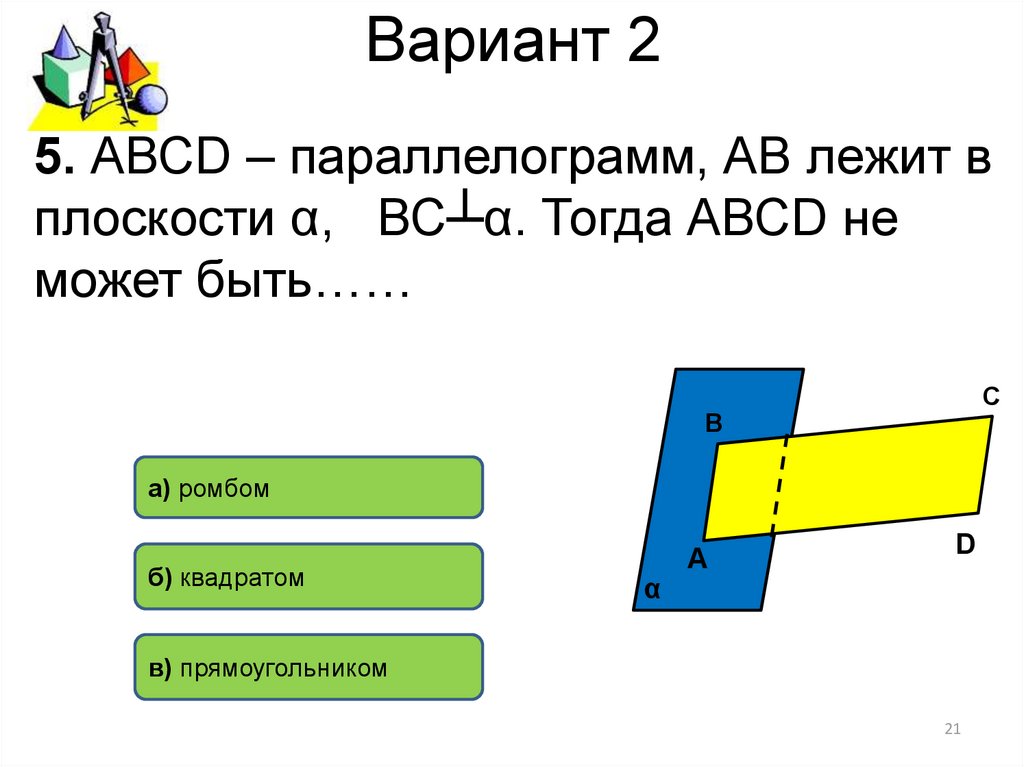
5. АВСD – параллелограмм, АВ лежит в
плоскости α, ВС┴α. Тогда АВСD не
может быть……
С
В
а) ромбом
б) квадратом
α
А
D
в) прямоугольником
21

22. Вариант 2

6. а║b а┴с. Тогда прямые b и c не могут
быть…..
а) параллельными
б) перпендикулярными
в) скрещивающимися
22

23. Вариант 2

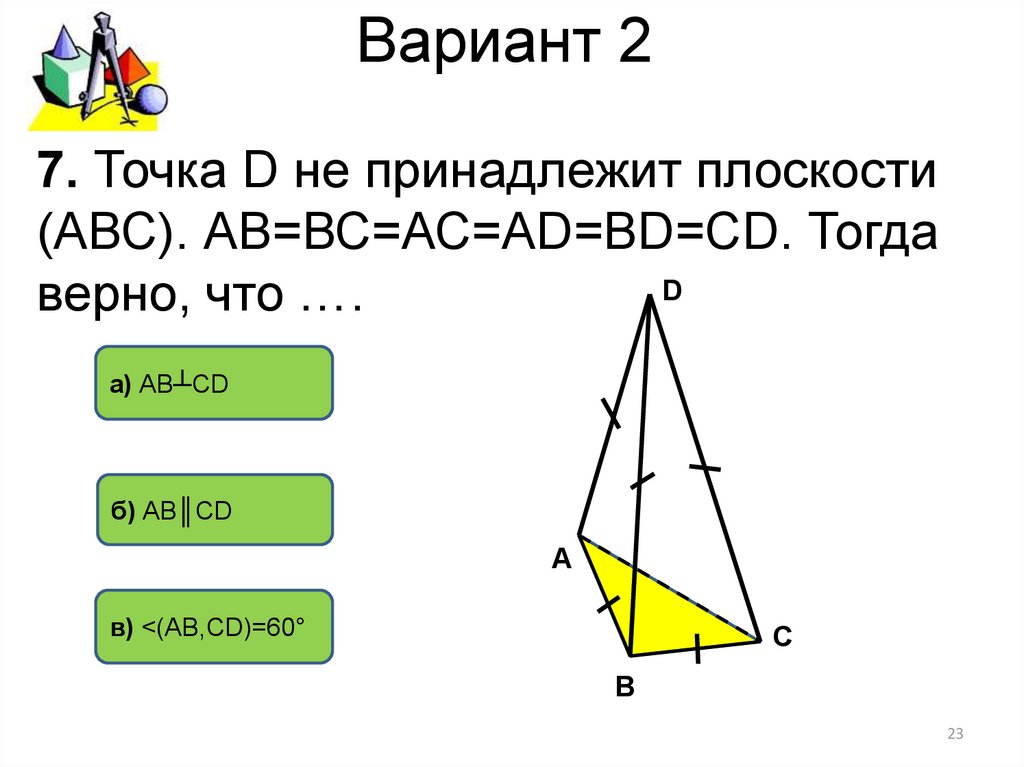
7. Точка D не принадлежит плоскости
(АВС). АВ=ВС=АС=АD=ВD=СD. Тогда
D
верно, что ….
а) АВ┴СD
б) АВ║СD
А
в) <(АВ,СD)=60°
С
В
23

24. Вариант 2

8. Какое утверждение неверное?
а) Через любую точку пространства проходит прямая,
перпендикулярная к данной плоскости, и притом только одна.
б) Через точку, не лежащую на данной прямой, можно построить
только одну плоскость, перпендикулярную данной прямой.
в) Через точку, не лежащую на данной прямой, можно построить
только одну прямую, перпендикулярную данной прямой.
24

25. Вариант 2

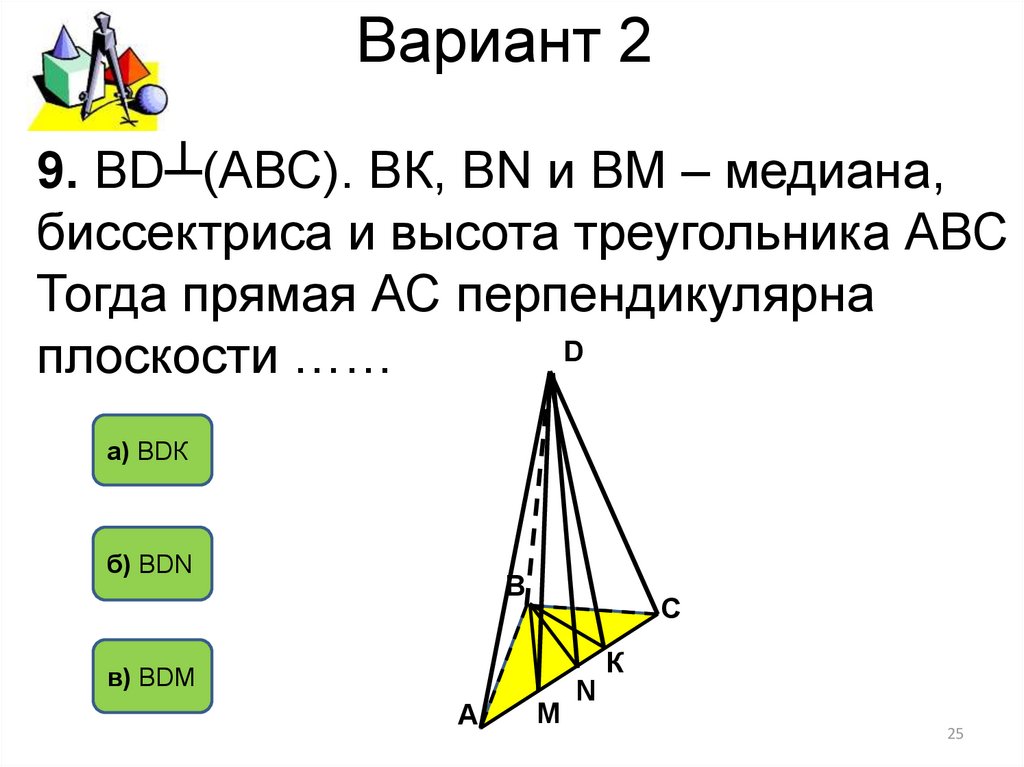
9. ВD┴(АВС). ВК, ВN и ВМ – медиана,
биссектриса и высота треугольника АВС
Тогда прямая АС перпендикулярна
D
плоскости ……
а) ВDК
б) BDN
В
С
К
в) BDМ
А
М
N
25

26. Вариант 2

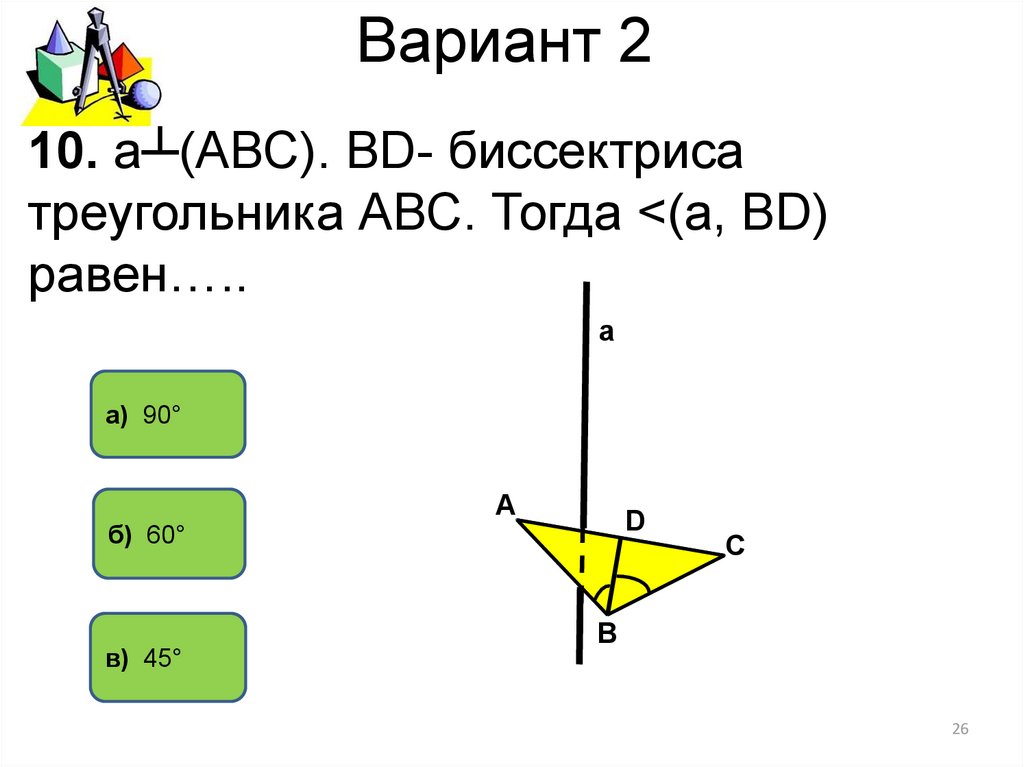
10. а┴(АВС). ВD- биссектриса
треугольника АВС. Тогда <(а, ВD)
равен…..
а
а) 90°
б) 60°
в) 45°
А
D
С
В
26

27. Вариант 2

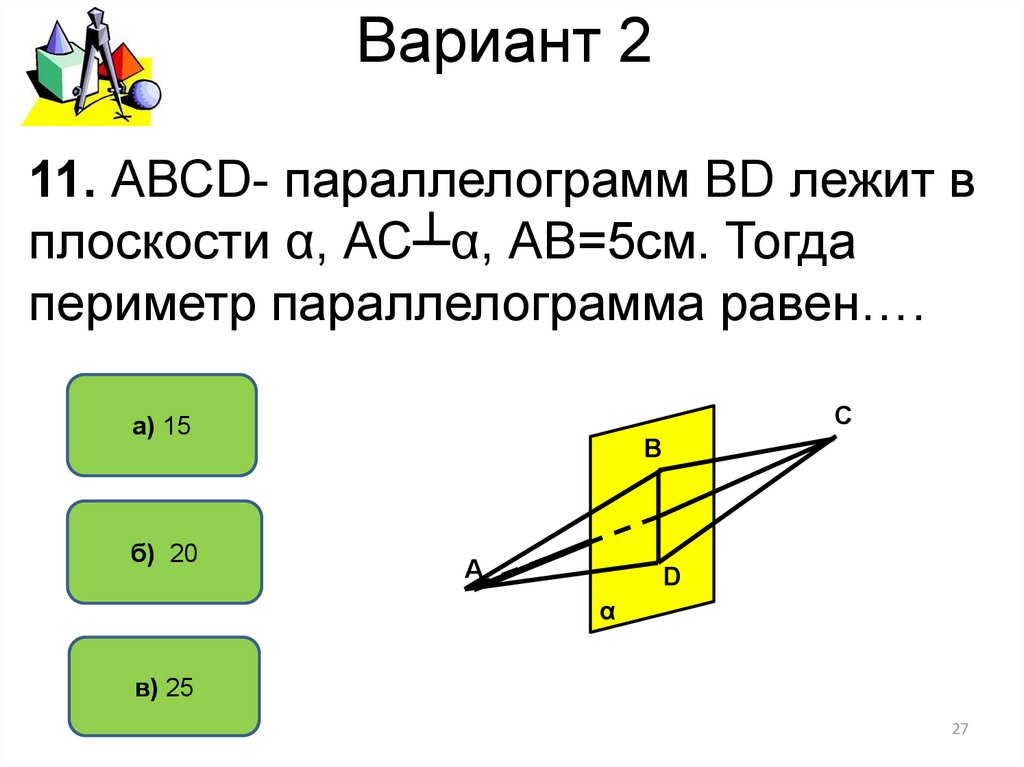
11. АВСD- параллелограмм ВD лежит в
плоскости α, АС┴α, АВ=5см. Тогда
периметр параллелограмма равен….
С
а) 15
б) 20
В
А
D
α
в) 25
27

28. Вариант 2

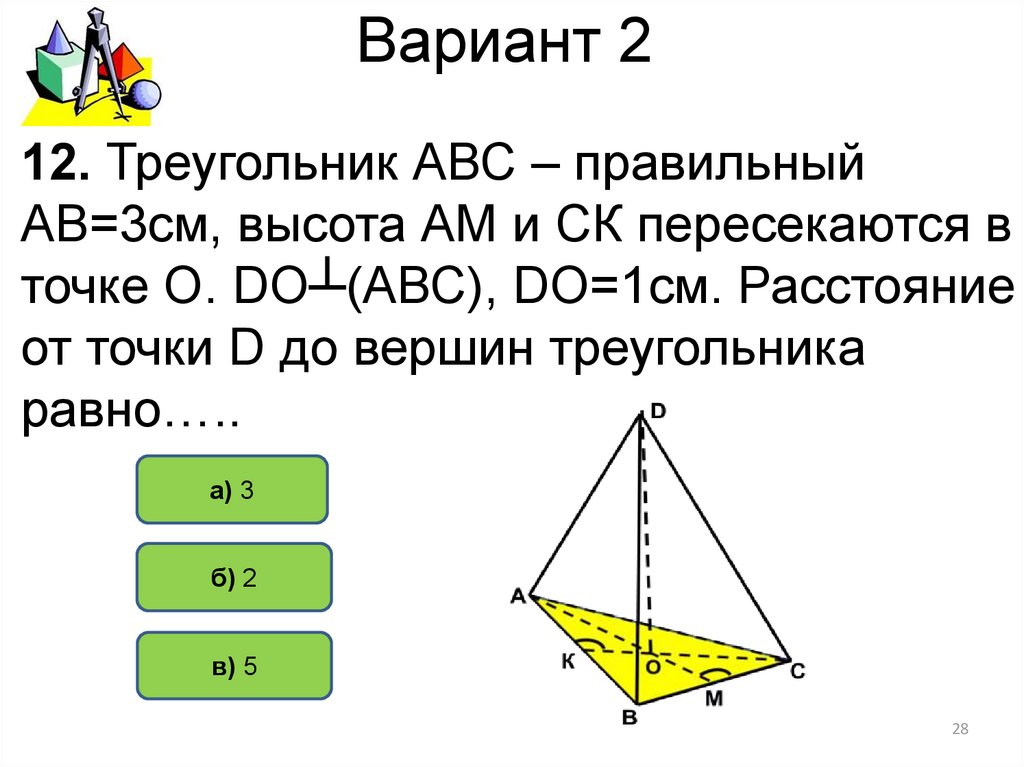
12. Треугольник АВС – правильный
АВ=3см, высота АМ и СК пересекаются в
точке О. DO┴(АВС), DO=1см. Расстояние
от точки D до вершин треугольника
равно…..
а) 3
б) 2
в) 5
28

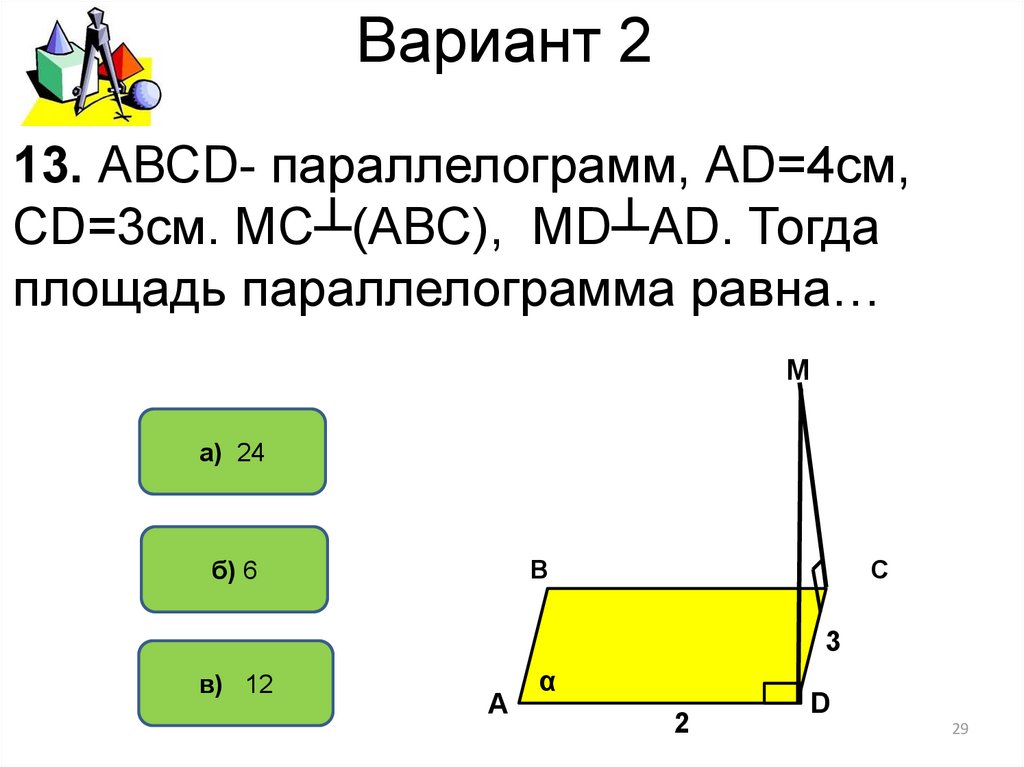
29. Вариант 2

13. АВСD- параллелограмм, АD=4см,
СD=3см. МС┴(АВС), МD┴АD. Тогда
площадь параллелограмма равна…
М
а) 24
В
б) 6
С
3
в) 12
А
α
2
D
29

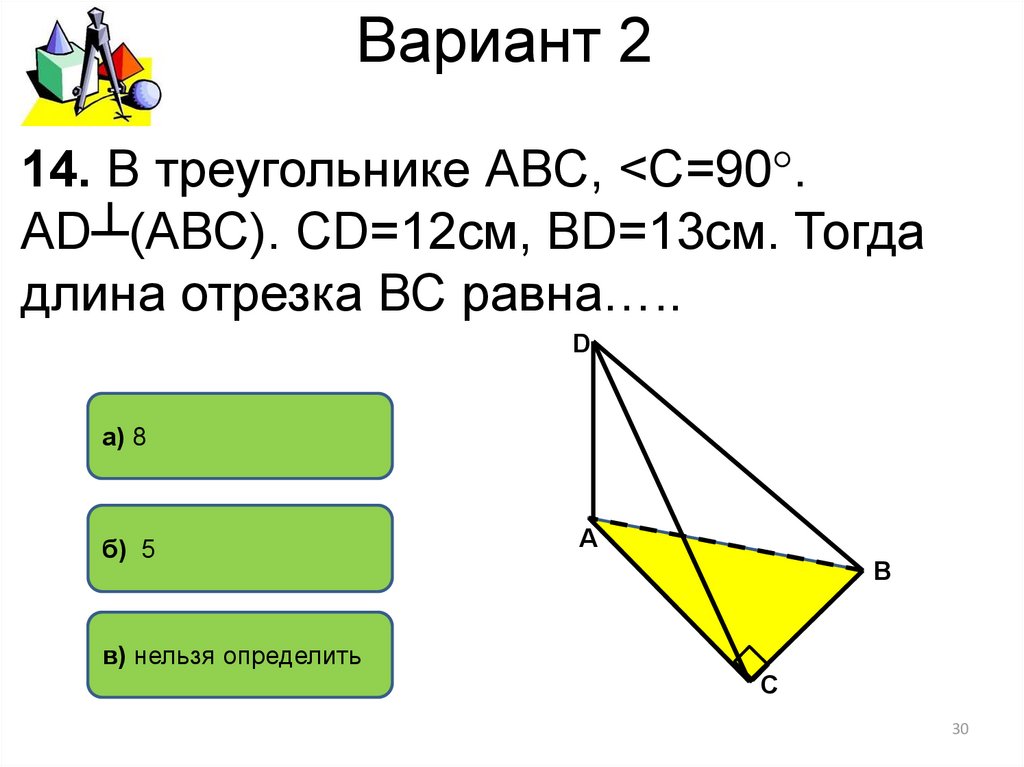
30. Вариант 2

14. В треугольнике АВС, <С=90°.
АD┴(АВС). СD=12см, ВD=13см. Тогда
длина отрезка ВС равна…..
D
а) 8
б) 5
А
В
в) нельзя определить
С
30

31.

Ключи к тесту: Перпендикулярные прямые в пространстве.
Перпендикулярность прямой и плоскости.
1 вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Отв.
в
в
а
б
в
а
б
б
б
а
б
б
в
б
2 вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Отв.
в
б
б
б
а
а
а
в
в
а
б
б
в
б
Литература
Г.И. Ковалева, Н.И. Мазурова Геометрия 10-11 классы. Тесты для текущего и обобщающего
контроля. Изд-во «Учитель», 2009г.
31