Similar presentations:
Grafice ale functiilor si rolul derivatelor
1. Grafice ale functiilor si Rolul derivatelor
RO
L
I
I
T
C
R
N
FU ELO
E AT
L
A IV
E R OS
C
I DE A G
F
R
A
L
D
GR OLUL I C E
R E
T
IS
SI
2. Rolul derivatei intai in studiu functiilor
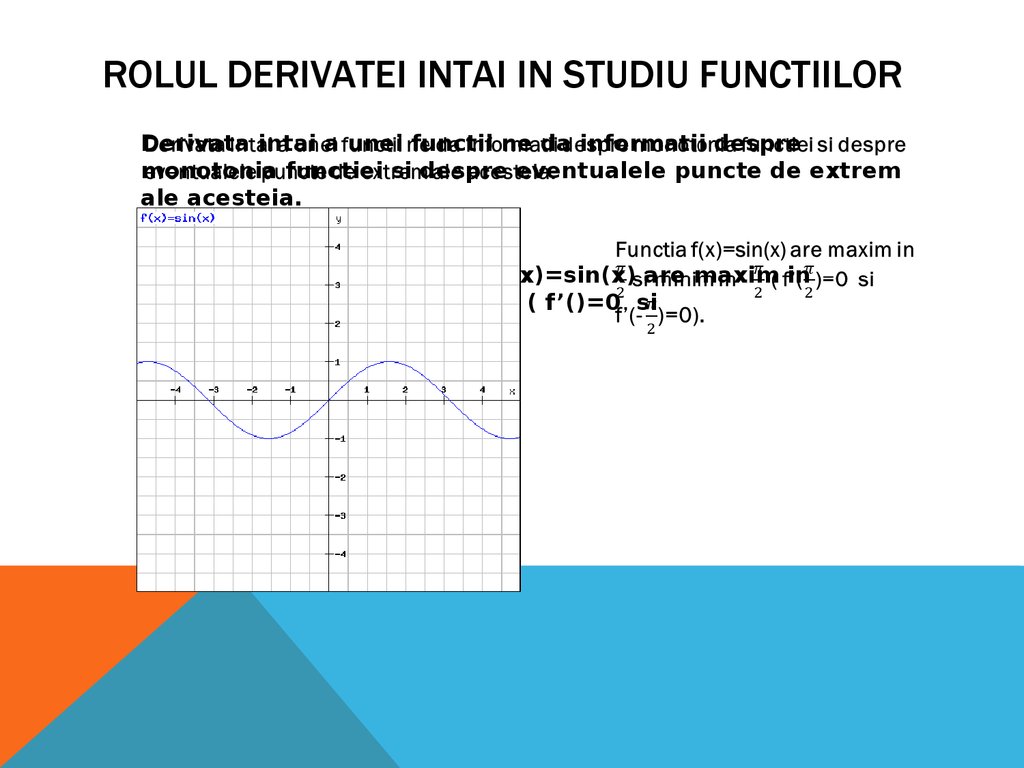
ROLUL DERIVATEI INTAI IN STUDIU FUNCTIILORDerivata intai a unei functii ne da informatii despre
monotonia functiei si despre eventualele puncte de extrem
ale acesteia.
Functia f(x)=sin(x) are maxim in
si minim in - ( f’()=0 si
f’(- )=0).
3. Consecinta Teoremei lui lagrange
CONSECINTA TEOREMEI LUI LAGRANGEConsecinta:
daca f’(x)>0, x I, f este strict crescatoare pe I
daca f’(x)<0, x I, f este strict descrescatoare pe I
4. Exemplu monotonie
EXEMPLU MONOTONIEf: [0,2] R, f(x)=+x
f’(x)=2x+1, f’(x)>0
f este strict crescatoare pe
[0,2]
5. Rolul derivatei a doua in studiu functiilor
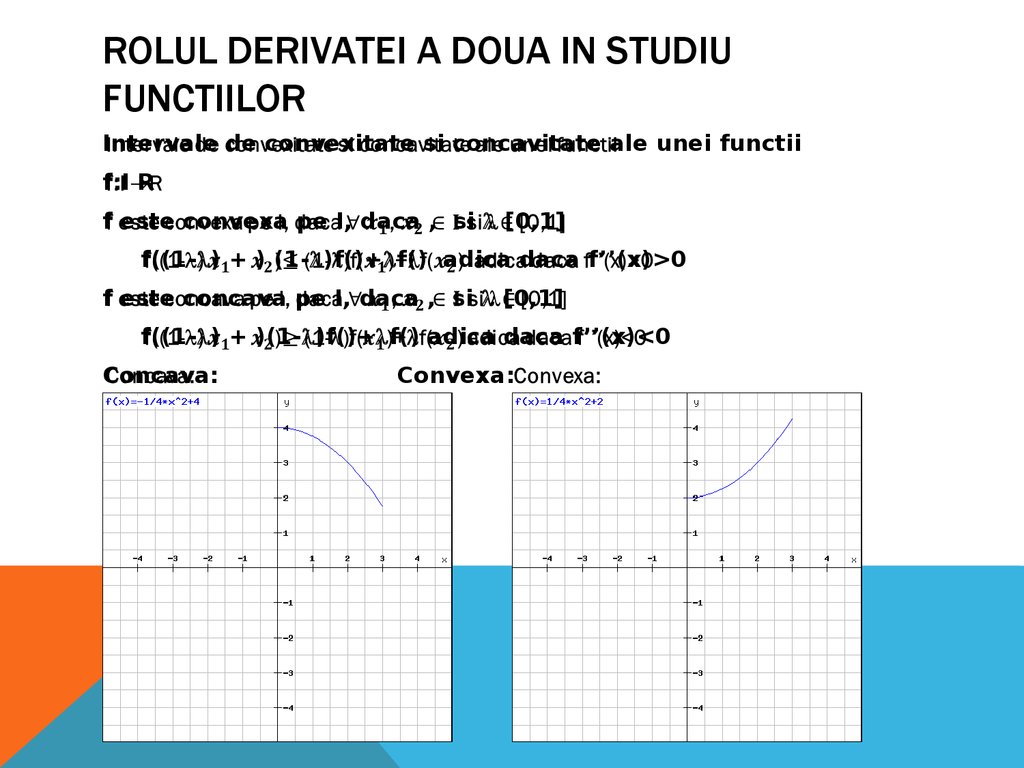
ROLUL DERIVATEI A DOUA IN STUDIUFUNCTIILOR
Intervale de convexitate si concavitate ale unei functii
f:I R
f este convexa pe I, daca , si [0,1]
f((1- ) + ) (1- )f()+ f() adica daca f’’(x)>0
f este concava pe I, daca , si [0,1]
f((1- ) + )(1- )f()+ f() adica daca f’’(x)<0
Concava:
Convexa:
6. Punctele de inflexiune ale unei functii
PUNCTELE DE INFLEXIUNE ALE UNEI FUNCTIIeste punct de inflexiune al functiei f daca f are derivata in
si daca pe I, de o perte a lui functia este convexa, iar de
cealalta parte a lui functia este concava.
=0 este punct de inflexiune
pentru f(x)= adica f’’(x)=0
7. Reprezentarea grafica a functiilor
REPREZENTAREA GRAFICA A FUNCTIILORI Domeniul de definitie (determinare, interesectii cu axele,
calcularea la capete si asimptote)
II Derivata intai (rezolvarea ecuatiei f’(x)=0, intervale de
monotonie)
IIDerivata a doua (rezolvarea ecuatiei f’’(x), intervale cu semn
constant)
IV Tabelul de variatie (valori remarcabile, f’(x), f’’(x), f(x))
V Trasarea graficului
8. Exemplu
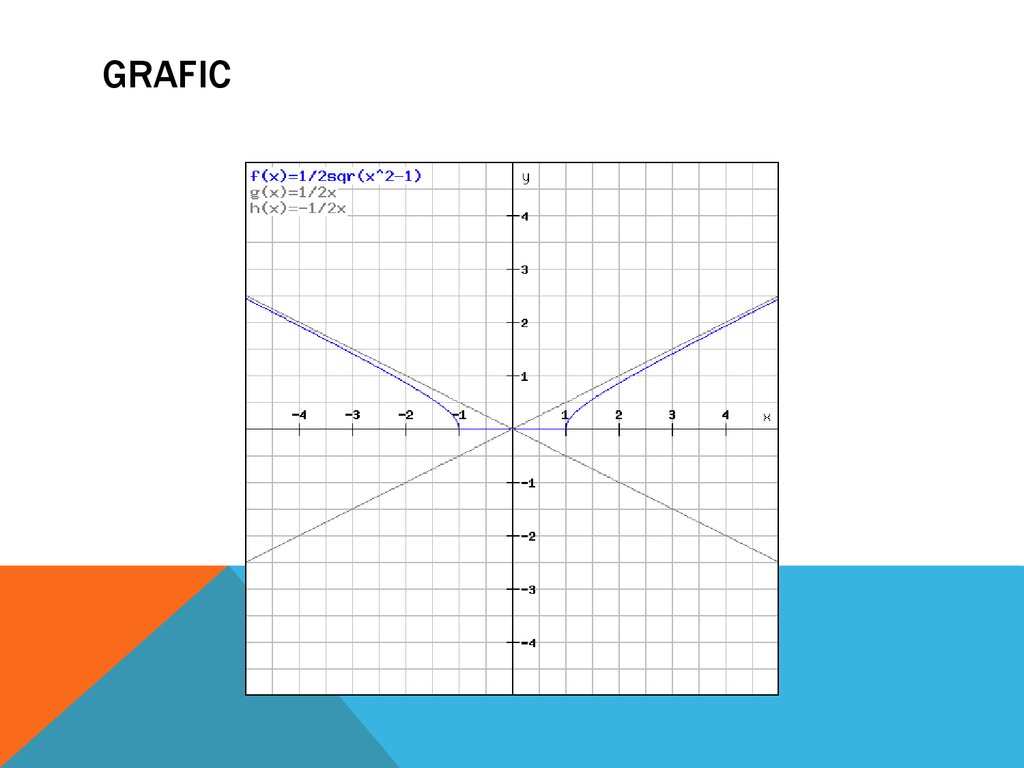
EXEMPLUf(x)=
I D=(-∞,-1]U[1, + ∞)
Intersecteaza Ox in (-1,0) si (1,0) dar nu si Oy pentru ca x0.
Asimptote oblice y= si y=
II f’(x)=0 nu are solutii.
III f’’(x)=0 nu are solutii.
x
IV
-∞
-1 |||
1
+∞
f’(x)
-
-∞ ||| ∞
-
-∞ ||| -∞
+
f’’(x)
+
f(x)
+∞
+∞
↘
0 ||| 0
↗
9. grafic
GRAFIC10. Bibliografie
BIBLIOGRAFIEMatematica – Manual pentru clasa a XI-a Editura Sigma 2003
Matematica clasa a XI-a “Elemente de analiza matematica”
Editura Carminis
Manual pentru clasa a XI-a “Elemente de analiza matematica”
Editura Mathpress 2003
Exercitii si probleme de clasa a XI-a (si nu numai) Editura Birchi
Gazeta Matematica Editie Electronica 1895-2004 Intuitext
Revista de Matematica din Timisoara Editie Electronica 19212006 Intuitext
http://rechneronline.de/function-graphs/







 mathematics
mathematics








