Similar presentations:
Newton’s binomial formula
1. “Newton’s binomial formula ”
2. Newton’s formula
Are loc următoarea:There is: Binomial’s theorem , a,bє Ł si nєAt*,
then
Teoremă a binomului .
Fie a, b , n
. Atunci :
a+b =C0n a n +C1n a n 1b+C2n a n 2b2 +..... + Ckna n k b k +.....+Cnn 1ab n 1 +Cnn bn
n
cunoscută sub denumirea de formula lui Newton.
also as
formula. fizician englez 1643-1727 .
Isaac Newton
matNewton’s
ematician, astronom,
known
Isaac Newton, English mathematician, astronomer,
physician (1643-1727)
Demonstraţie cu metoda inducţiei matematice:
Demonstration
mathematic
induction method:
Etapa
I. Verificare:using
P 1 : ...munca
independentă...
Step I. Verification : P(1): ……. Independent work …..
2
3. Theorem demonstration :
Fie P n : a+b =C0n a n +C1n a n 1b+C2n a n 2 b 2 +..... + Ckn a n k b k +.....+Cnn bn , n .n
I. Verificare: P 1 :
a+b
1
=C10a+C11b
A ;
II. P n P n+1 :
P n+1 : a+b
n +1
n +1
=C0n+1a n +1 +C1n+1a n b+.....Ckn+1a n +1 k b k +.....+Cn+1
b
?
n+1
P n+1 : a+b a+b = a+b C0n a n +C1n a n 1b+.....+Ckn a n k b k +.....+Cnn b n =
n
=C0n a n +1 +C1n a n b+....+Ckn a n k +1b k +...+Cnn b n +C0n a n b+C1n a n 1b2 +.....+
+Ckn a n k b k +1 +.....+Cnn b n +1
a+b
n +1
= C0n a n +1 + C1n +C0n a n b+ C2n +C1n a n 1b 2 +....+ Cnn Cnn b n +1
C0n+1
C1n +1
Cn2 +1
A .
Cn+1
n+1
Conform principiului inducţiei matematice rezultă că P n este adevărată n
3
.
4. Specifications regarding Newton’s formula:
1kkn
n
0
10
1) Coeficienţii
C
,
C
,
...C
,...,
C
se numesc
coeficienţi
binomiali
1) Coeficienţii
C
,
C
,
...C
,...,
C
se
numesc
coeficienţi
binomiali
n
n
n
n
0 n 1 n
k n
n n
1) Coeficienţii C n , Cn0 , ...C
coeficienţi binomiali
1 n ,..., kC n se numesc
n
dezvoltării
în
număr
de
n
+1
.
1) aiCoeficienţii
Cşinîn
,sunt
Cnumăr
,
...C
,...,
C
se
numesc
coeficienţi
binomiali
ai dezvoltării
şi sunt
de
n
+1
.
1.the
coefficients
are
called
binomial
coefficients
n
n
n
dezvoltării şi sunt în număr de n +1 .
of ai
the
development
andcoeficientul
are
in number
A
sedistincţie
face distincţie
între
coeficientul
al termen
unui termen
A se
face
al unui
şi şi
ai
dezvoltării
şi între
sunt
în
număr
de binomial
n +1binomial
. of n+1.
A se face distincţie între coeficientul binomial al unui termen şi
A coeficientul
se face distincţie
între
binomial al unui termen şi
nucmeri
c coeficientul
al acelui
termen!
nu
al
termen!
Is coeficientul
necessary
tomeri
make
aacelui
distinction
between
the binomial coefficient
coeficientul numeric al acelui termen!
coeficientul
meric al acelui
termen! of the same term.
of a term
and thenunumerical
coefficient
2)n+1
Ceitermeni
n+1 termeni
2) Cei
sunt: sunt:
2.2)Those
n+1
are
Cei 0n+1
termeni
sunt:n 1 2 n 2 22 n 2 2
0 n termeni
n n
n n+1
1 n 1 1 sunt:
k n-k kk n-k k
n n
2)
Cei
T
=C
a
,
T
=C
a
b,
T
=C
a
b
,....,
T
=
C
a
b
,....,
T
=C
T1 =C
a
,
T
=C
a
b,
T
=C
a
b
,....,
T
=
C
a
b
,....,
T
=C
b
.
1
n
2
n
3
n
k+1
n
n+1
nb .
n
2
n
3
n
k+1
n
n+1
n
0 n
1 n 1
2 n 2 2
k n-k k
n n
T1 =Cn a , 0T2n=Cn a 1b, nT
=C a b ,...., Tk+1 = Cn a b
,...., Tn+1 =Cn b . n n
T1 =Cn a , T2 =Cn a 13b, Tn3 =Cn2 a n 2 b 2 ,....,
Tk+1 = Cnk an-k bk ,....,
Tn+1 =Cn b .
0
20
42
4
3) Numerele
naturale
Cn numesc
... seare
numesc
3) Numerele
naturale
C
, CC , ,CC..., se
3. The
natural
numbers
called binomial
0 n 2 nn 4 nn
3) Numerele naturale Cn , Cn0 , Cn2... se4 numesc
1
31
53
5
coefficients
of odd
rank,
numbers
3) coeficienţi
Numerele
naturale
Cde
, imp
Cn , the
Cimp
se
numesc
coeficienţi
binomiali
de rang
ar,
iar
numerele
C
,
C
,
C
....
binomiali
rang
ar,
iar numerele
C
,
C
,
C
nand
n ...
n
n
n
n
n
n ....
1
3
5
coeficienţi
binomiali de
rang impar,ofiareven
numerele
C , C , C ....
are
binomial
coefficients
rank.
secalled
numesc
coeficienţi
binomiali
de rang
par.
se numesc
coeficienţi
binomiali
rang
par. n C1n, C3n, C5 ....
coeficienţi
binomiali
de rang
imp
ar,deiar
numerele
n
n
se numesc coeficienţi binomiali de rang par.
numesc coeficienţi
binomiali
de rangofpar.
4. In se
Newton’s
formula the
exponents
a powers are
n
4) În4)
formula
lui nNewton
exponenţii
puterilor
a descresc
În from
formula
lui 0,
Newton
exponenţii
puterilor
lui a descresc
decreasing
to
and
exponents
oflui
b power
are
4) În formula
lui Newton
exponenţii puterilor lui a descresc
increasing
from
toNewton
n.
de la
nÎnla
0,
iar0,0
exponenţii
puterilor
lui bputerilor
cresc
delui
la ade
0 descresc
lalan.0 la n.
laformula
n la
iar
exponenţii
puterilor
lui b cresc
4) de
lui
exponenţii
de la n la 0, iar exponenţii puterilor lui b cresc de la 0 la n.
de la n la 0, iar exponenţii puterilor lui b cresc de la 0 la n.
4
5. Specifications regarding Newton’s formula ( continuation)
ţii binomiali ai termenilor extremi şi cei ai termenilor egal depărtaţi5) Coeficienţii
binomiali
ai1 termenilor
egal depărtaţi
5. The
the
terms
those equally
distant
1
n of
2 extreme
n 2 extremi
kşi cei
nand
kai termenilor
iextremi
binomiali
aibinomial
termenilor
extremi
cei
ai
termenilor
egal
depărtaţi
sunt
egali:
C0ncoefficients
=Cnn , Cşi
=C
,
C
=C
,
....
,
C
=C
.
n
n
n
n0
n
1n
nn 1
2
n 2
k
n k
from ai
the
terms
are
equal
:
binomiali
termenilor
extremi
şi
cei
ai
termenilor
egal
depărtaţi
deextreme
termenii
extremi
sunt
egali:
C
=C
,
C
=C
0
n
1
n 1
2
n 2n
kn
n n k , C n =C n , .... , C n =C n .
n
xtremi sunt egali: Cn =Cn , Cn =Cn , Cn =Cn , .... , Cn =Cn .
n
1
n 2
n k
xtremi6.sunt
egali:
C0n =C
, C1n =Cnnis
,even,
C2n =Cn=2k,
, ....then
, Ckn =C
.
n
n
n development
If
the
power
exponent
the
has 2k+1
onentul puterii este par n=2k atunci dezvoltarea are 2k+1 termeni,
6) Dacă
exponentul
puterii
estethe
par highest
n=2k atunci
dezvoltarea
are 2k+1 termeni,
then=2k
middle
term
has
binominal
coefficient
:
ul
dinterms,
mijlocare
coeficientul
binomial
cel
mai mare:
nentul
puterii and
este
par
atunci
dezvoltarea
are 2k+1 termeni,
iarpar
termenul
din mijlocare
coeficientul
cel mai mare:
entul puterii este
n=2k
atunci
dezvoltarea
are 2k+1binomial
termeni,
n
din mijlocare coeficientul
cel mai
C0n binomial
C1n C2n ....
Ckn mare:
Ck+1
....
C
.
n 0
n2
1
k
k+1
din mijlocare coeficientul
binomial
cel
mai
mare:
C
C
C
.... Cnn .
0
1
2
k
k+1 n
n n n .... Cn Cn
onentul
puterii
este impar
n=2k+1
atunci
are
Cexponent
C
Cnis
....
Cndezvoltarea
Cn ....then
C2k+2
.
If the
power
odd,
0n
1n
2
k n=2k+1,
k+1
n n the development has 2k+2
Dacă
puterii
Cnexponentul
Cn Cn ....
Cn este
Cnimpar
....n=2k+1
Cn . atunci dezvoltarea are 2k+2
xistă
doi
termeni
mijlocul
cu in
coeficienţii
entulterms
puterii
este la
impar
n=2k+1
atunci
dezvoltarea
are binomiali
2k+2of the development with
and
there
aredezvoltării
two
terms
the middle
termeni
există
doi
la mijlocul
dezvoltării
cu
entul puterii este
imparşin=2k+1
atunci
dezvoltarea
are
0
1 termeni
2
k
k+1 2k+2
k+2
n coeficienţii binomiali
equally
and
of
highest
value
stă doi
termeni
la mijloculcoefficients
cu
coeficienţii
binomiali
aloare
cea
mai binomial
mare:
Cdezvoltării
C
C
....
C
=C
C
....
C
.
n
n
n
n
n
n 1
0
2 n
n
tă doi termeniegali
la mijlocul
dezvoltării
binomiali
şi de valoare
mare:
Cn Cnn.... Cnk =Cnk+1 Ck+2
0
1 cea mai
2cu coeficienţii
k
k+1 C
k+2
n
n .... Cn .
oare cea mai mare:
C0n C1 n C2n .... Ckn =Ck+1
Ck+2
n
n .... Cnn .
oare cea mai mare:
Cn Cn Cn .... Cn =Cn Cn .... Cn .
portant în rezolvarea problemelor
legate de binomul lui Newton
7. An important
role, in resolving
problems
with
Newton’s
binomial,
7) Un rol important
în rezolvarea
problemelorrelated
legate de
binomul
lui Newton
kbinomul
n-k k lui Newton
ortant
în
rezolvarea
problemelor
legate
de
menulisgeneral
deby
rang
k+1:
Tk+1term
=C n ahaving
b , k the
∈ 0,rank
1, 2, ....,
n k n-k k
the
general
k+1:
rtant în played
rezolvarea
problemelor
legate
de
binomul
lui
Newton
îl joacă termenul general kden-krang
k+1:
T =C n a b , k ∈ 0, 1, 2, ...., n
enul general de rang k+1:
Tk+1 =Ckn an-k bkk , k ∈ 0, 1, 2, k+1
...., n
nul general de rang k+1:
Tk+1 =C n a b , k ∈ 0, 1, 2, ...., n
5
6. Example:
12
3
4
5
6
6
2 6 32x 3+C
3 6 42x
4 6 452x +C
5 6 62x 5 6
1 1+2x
2x+C
+C
222x +C
1
1 6 6=1+C
2
3
4
5
6
6
6
2 2 22 3 3 3
3 3 33 4 4 4
4 4 44 5 5 5
5 5 55 6 6 6
6 6 66
6 6 =1+C
1 111 2x
2 222
1 1+2x
1+2x
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
+2x =1+C
2x+C
+C
2x
+C
2x
+C
2x
+C
3
4
5
6
6
6
6
6
6
6
6
2
3
4
5
6
6
2
3
4
5
6
6
6
6
6
6
6
=1+C
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
1 1 11+2x
=1+C
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
6 6 66 2x+C
2 6 6 2x
36 6 2x
46 6 2x
56 6 2x
6
1+2x
=1+C
2 +C
3 +C
161 66 2x
2
3
4 4 +C
12x+C
22x
32x
42x
5 5 5 +C
6 6 6
6+C
6+C
6+C
6+C
1
1+2x
=1+C
2x
2x
6
6
6
6
6
6
1
1+2x
=1+C
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
1
1+2x
=1+C
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
1
1+2x
=1+C
2x+C
2x
+C
2x
+C
2x
+C
2x
+C
2x
Astfel :
6 66
6 66 6 66 6 66 6 66 6 66
Astfel
:
:
Thus:
Astfel
Astfel
: ::3:
Astfel
Astfel
3
Astfel
Astfel
Astfel
:32x:3 :3 =160x
3
a)3 T4 =C
3
3
633
3 33 3
3=C
3 33 3
a)
T
2x
=160x
=C6 2x
=160x
3
4
6
a) a)a)
Ta)4 T
=C
=160x
3 33
T4T4=C
=C
=160x
32x
62x
2x
3=160x
32x
3 33
6 6 2x
=C
=160x
2
46a)
T
=C
2x
=160x
a)
T
=C
2x
=160x
a)
T
=C
=160x
6
b) coeficientul
al termenului T3 este C
=15
4 4 4 6 6binomial
22
6
2 C
2C
22 =15
eficientul
binomial
al
termenului
T
este
b)
coeficientul
binomial
al
termenului
T
este
3este
62=15
3este
6=15
coeficientul
binomial
b) b)
coeficientul
binomial
al al
termenului
C6C=15
b)
coeficientul
binomial
alaltermenului
termenului
T3T3is
este
CC
b)
The
binomial
coefficient
of 4 T3 T
22
6 6=15
b)
coeficientul
binomial
termenului
este
=15
4
3T T
6C C
b)
coeficientul
binomial
al4termenului
termenului
T
este
C
=15
coeficientul
binomial
al
este
b) b)
coeficientul
binomial
termenului
este
=15
c) coeficientul
termenului
T5 al
este
C
2
=240
3
6=15
3
6
3
6
4
4
4
6 4 44 4 4
4
ficientul
termenului
T
este
C
2
=240
c)coeficientul
coeficientul
termenului
T5este
este
C2 64 2=240
24=240
=240
5 ofT T
termenului
c) c)c)
coeficientul
termenului
este
C66CC
C
coeficientul
termenului
este
4=240
c)
The
coefficient
5T
6 6 242=240
5 T
5 is
coeficientul
termenului
este
5T T
6C C
coeficientul
este
244=240
=240
coeficientul
c) c)c)
coeficientul
este
6264 4 2=240
d) termenul
liber esttermenului
e termenului
Ttermenului
55 este
5 T
6C
1 =1
menul liber
est
e
T
=1
d)
termenul
liber
est
e
T
=1
1 estest
1=1
liber
TT1T1=1
d) d)
termenul
liber
eest
Te1ee=1
d)
termenul
liber
5
d)termenul
termenul
liber
est
5
5
1 5=1
d)
termenul
liber
est
=1
d)
termenul
liber
est
TT11=1
d)
The
free
term
d)
termenul
liber
est
e
Te1eeste
=1
5
e) termenul care conţine
x
T
C
2x
192x
5
5
5
5
5
5
6
5 55
5
5 55
5 5x5Teste
5 6C
5192x
5 2x
menul care
conţine
x
este
C
5
e)
termenul
care
conţine
T
2x
192x
5
5
5
65T 5T
6 6C
55
5192x
care
conţine
192x
e) e)e)
termenul
care
conţine
x xxeste
termenul
care
conţine
este
T6T6C
5 2x
TC6T 2x
2x
5 192x
52x
5 55
6 59
6 6 2x
e)termenul
termenul
care
conţine
x este
este
6C
192x
6
6
e)
termenul
care
conţine
x
este
C
2x
192x
e)
termenul
care
conţine
x
este
C
2x
192x
e)
termenul
care
conţine
x
este
T
C
192x
e)
The
term
that
contain
is
e) nu există termen care conţine
6 66 6 66
9 x
9 9x99
există termen
care
conţine
x
e)
nu
există
termen
care
conţine
9
există
termen
care
conţine
e) e)e)
nu
există
termen
care
conţine
x xxx 9 99
nu
există
termen
care
conţine
e)nu
nue)
există
termen
care
conţine
e)
nu
există
termen
care
conţine
x xx
nu
există
termen
care
conţine
e)
nu
există
termen
care
conţine
f) there is no term that contains
6
2
3
4
5
6
6
6
7. Identities in the combination calculus
Utilizând formula lui Newton de dezvoltare a binomului a + bn
Identities in the combination calculus
0 n
1 n 1
2 n 2 2
k n k k
n 1 n 1
n n
n
a+b
=C
a
+C
a
b+C
a
b
+.....C
a
b
+.....+C
ab
+C
b
,
n
n
n
n
n
n
Utilizând formula lui Newton de dezvoltare a binomului a + b
n
se pot
deduce
câteva
identităţi
interesante
în
care
intervin
coeficinţii
binomiali.
n
n
Utilizând
de
a binomului
0 nNewton’s
1 n lui
1 formula
2 n lui
2deNewton
2for
k ndezvoltare
binomului
k kdevelopment
n+ 1b n 1 a +
n bn
Using
the
formula
binomial
Utilizând
formula
Newton
dezvoltare
a
a
a+b
=C
a
+C
a
b+C
a
b
+.....C
a
b
+.....+C
ab
+C
n
n
n
n
n
nb ,
n
2 n
k n kn 1k n 1
1=C
n 01a n +C
21 a
n n2 1 b+C
2
k2 b
n 2k+.....C
k
nn n1 ab n 1 +Cn b n
a+b
a
a
b
+.....+C
n
n
n
a +Cn identităţi
a n b+Cn an interesante
b +.....C
+.....+C
+Cnnb , binomi
=Ccâteva
n a în b
n ab coeficinţii
se pot a+b
deduce
care
intervin
Particularizând
înseformula
lui
Newton
a b 1interesante
pot
deduce
câtevainteresante
identităţi
în care
intervinbinomiali.
coeficinţii bi
se pot deduce
câteva
identităţi
îngăsim:
care intervin
coeficinţii
n
0 n
n
n
There can be deduced some interesting identities in which
n
binomial 2coefficients
C0n + C1n + intervene
Cn2 + ..... + C. nn 1 + Cnn
•Particularizând
în formula
lui
Newton
ba=b=1
b 1 găsim:
1 agăsim:
Particularizând
înluiformula
lui
b 1 găsim:
Particularizând
în
Newton
aa Newton
Particularised
informula
Newton’s
formula
n we find :
Suma coeficienţilor
binomiali 2ai
dezvoltării
esten 2 n n 1 n
02
1
2n n1 1
n n 0 0 1 n1
.....
2 2 C nC+n +C2Cn n+ +CCCnnn ++ C.....
....
+Cn+CCn n + Cn
n ++CC
nn n++
n
n
n
Suma
coeficienţilor
binomiali
ai
dezvoltării
este
2
Suma
coeficienţilor
binomiali
ai
dezvoltării
este
2
the sum
of the
development
of theaibinomial
is 2ⁿ
Suma
coeficienţilor
binomiali
dezvoltăriicoefficients
este 2
În aceeaşi
formulă
a lui
Newtontaking
luând a a=1
1 şiand
b b=-1
1 obţinem:
• In the
same
formula
we obtain:
În
aceeaşi
formulă
a2 nluiluân
Newto
1 şi b 1 obţinem:
În aceeaşi
formulă
d a nn1luân
şin b d a 1 obţinem:
0 a lui
1Newto
0 aCnlui C
..... d a1 C1 nşi b 1 obţinem:
n + Cnn luân
În aceeaşi formulă
Newto
n
02
1
2n
n
0
1
n
0
C
C
+
C
.....
1
0 Cn Cn + nn .....n 1 n Cn Cn
the alternating
sum ofa the
binomial
coefficients
Suma alternantă
coeficienţilor
binomiali
0 is 0
n este
7
0
1
2
n
a coeficienţilor
binomiali
este
0
Suma
binomiali
este
0
0 alternantă
Cn Suma
Cn aalternantă
+coeficienţilor
Cn .....
1
C
n
8. Identities in the combination calculus( continuation)
Adunând cele două sume membru cu membru obţinem:Adunând
cele
două
sume
membru
cucumembru
n
0
1
2
n 1
n obţinem:
Adunând
cele
sume
membru
membru
obţinem:
Adding
the
two
sums
member
by
member
obtain:
cele
două
sume
membru
cu
membru
obţinem:
2Adunând
Cdouă
+
C
+
C
+
.....
+
C
+
C
cele
sume
membru
cu we
membru
obţinem:
nAdunând
n
n n 1 două
n
n
n
0
1
2
n
22n CCn 0++CnCn 1++C0Cnn2++.....
n n 1
1 0+C
2 n1 n 1+ C
nn 1
nC
2+
n
n
.....
+
C
+
C
2
C
+
C
+
C
+
.....
+
C
0
1
2
n
n
n
n .....
+
C
+
C
n2 n C
n n +C
n nn + C n +
n
nn
n
01 Cn 2 Cn + Cn n .....
0
n 1 C n
n
n
00 CCn 0 CCn 1++C0Cn 2 .....
1 0 1
2 1 C n n 2
n
n
n
.....
1
C
0
C
C
+
C
.....
1
C
n
n
n n ..... n 1 C n
n 0n C
n n C
n n +C
n
0
2
4
6
n
02 2
2 C 4+ C 6 + C + C + ..... sau
22n 22 CCn 0n++CCn 2++nC0nCn 4++C2nCn06++.....
4n 2 sau
6n 4
6 sau
.sume
....
sau
Cn cele
+n2C C
+n +CC
+ +C
+
.....
2Adunând
n 2n 2
n două
n
n
C
+
C
.... membru
sau
membru
obţinem:
n
n
n
n + .cu
n
1
0
2
4
6
2
C6 n 4++....
....6
C0nn4n 1+4+CC2nn60 +
....
Or : n 22n0 n1 1 C1C0n 022+n+C
2+C
61+C
12n
4n 2+
nC
C
+
C
+
C
+
....
C
+
C
+
C
+
2n n+ CC
n nn ++C
nC
n n + C n + ....
2 Cn + Cn +n Cn n+ .....
n n+ C
n
n 1
n 1
Suma
coeficienţilor
binomiali
de
rang
impar
este
2
n 1 este
n 1
Suma
coeficienţilor
binomiali
de
rang
impar
2
the
sum
of
the
binomial
coefficients
of
odd
rank
is
Suma coeficienţilor
binomiali
de nrang
este
2 este
Suma
coeficienţilor
binomiali
de rang
impar
2 este 2n 1
0
1
2coeficienţilor
n impar
Suma
binomiali
de
rang
impar
0 două
Cn sume
Cn +obţinem:
Cn ..... 1 Cn
Scăzând cele
Scăzând
cele două
sume
obţinem:
două
sume
obţinem:
Scăzând
cele
sume
obţinem:
Subtracting
the
two
sum
we
obtain
Scăzând
cele
două
sume
obţinem:
n
1 n
3
5
7
0
2
4
6
2 n 2 Cn 21nn+ C n23+ C
Cnn 5+
+C
C33 nn1 7+
.....
55 3 +sau
77 5 + .....
+
C
C
sau
n11 C
7 sau
n
n
2 2 C22n + C
+
+
C
+
.....
sau
2
C
+
C
+
C
+
C
+
.....
2
2
C
+
C
+
C
+
C
+
..... sau
n
n
n
2 Cn + C n + Cn + Cn + ..... sau
or
n
n 1
n 1
n n
nn
nn
1
3
5
n 1 nn 11n 3 1n0n 15
n n 1 n
n1n n
n
7
3 2n1 7
n3nnn
C + C + C + C + ...5 4.3 7 65
CC
.......
. 7 + ....
2 C 22+ C C+2CC++ C+CCC+++C+CC
5n+.+
7n++
+
C
+
C
n...
n
n+ C n +
2
C
+
C
+
C
n ....
1 n
n
n
n
n
Suma coeficienţilor binomiali de rang par este 2 n 1
n 1 n 1 n 1
Suma
coeficienţilor
binomiali
de
rang
par
est
e
2
Suma coeficienţilor
binomiali
de
rang
par
est
e
2
binomiali
deimpar
rang
Suma
coeficienţilor
par
binomiali
deofrang
este
nest
12e 2
The sum Suma
of thecoeficienţilor
binomial
coefficients
even
rank
is
2
8
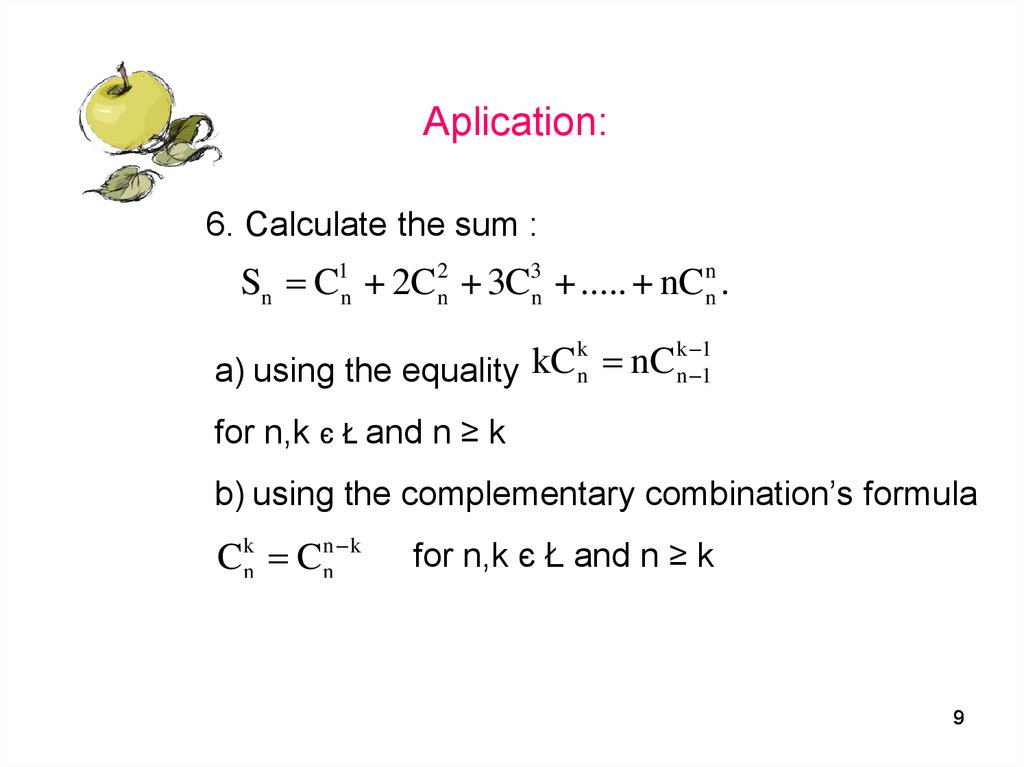
9. Aplication:
6Să Săcalculeze
6.6 Calculate
the
sumsuma:
: suma:
se se
calculeze
6 Să 1se calculeze
suma:
2
3
n
1
2
3
n
S
C
+
2C
+
3C
+
.....
+
nC
n2C 2+n3C 3+n..... + nC .n n .
SSn n CCn 1++
2Cn n + 3Cn n + ..... +k nCn n . k 1
n
n
k n nC
k 1 n 1
a) utilizând
egalitatea
kC
k
a)a)
utilizând
egalitatea
kC
nC
the egalitatea
equality kCn nCn k1 1
a) using
utilizând
n
n 1
pentru
n,k
,
n
k;
pentru
for
n,kn,k
єn,k
Ł
and
pentru
n, ,n≥n k k;k;
b)
utilizând
formula
combinărilor
complementare:
b)b)
utilizând
formula
combinărilor
complementare:
the
complementary
combination’s
formula
b) using
utilizând
formula
combinărilor
complementare:
k
n k
n Ck
pentru n,k , n k;
k n C n n nk pentru n,k , n k;
CCkn C
for n,k
C pentru
n,kє Ł and
, n n ≥k;k
n
n
9
10. Answer:
a) Demonstrareaofformulei:a) demonstration
the formula
a) Demonstrarea formulei:
n n 1 !
n!
k
kCnk k
k
n n 1 !
n!
kCn k k!. n k ! k k k 1 ! n k !
k!. n k !
k k 1 ! n k !
n 1 !
k 1
n
nC
n 1 !
n
k
1
n k 1 ! n k ! nCn 11
k 1 ! n k !
Astfel suma se rescrie:
Thus
the suma
sum isserewritten
Astfel
rescrie:
0
Sn nC0n 1 + nC11n 1 + nCn22 1 + .... + nC nnn 111
Sn nC
+ 1nCn 1 +2 nCn 1 + ....n+ 1 nC n 1 n 1
0 n 1
n C0n 1 + C1n 1 + C2n 1 + .... + C nn 11 n 2n 1
n Cn 1 + Cn 1 + Cn 1 + .... + C n 1 n 2
10
11. Test
141 3
Fie binomul x , x 0.
x 1 3 14
Fie binomul x , x 0.
1)
Câţi
termeni are
x
It is given the binomial
: dezvoltarea?
1. How many
terms
the
development
has?
1) Câţi
termeni
are
dezvoltarea?
2) Care
estedoes
rangul
termenului
din mijloc?
2.Which is the2)
rank
ofeste
therangul
middletermenului
term? din mijloc?
Care
3) the
Caresum
este of
suma
binomialiof
ai this
acestui binom
3. Which is
the coeficienţilor
binomial coefficients
3) Care
este sumaterm
coeficienţilor
binomiali
k n kai kacestui b
binomial?Folosind
Using
the
general
formula,
formul termenului general, Tk+1 =Cn a bk naflaţi:
k k
find out :
Folosind formul termenului general,
T
=C
a
b af
k+1
n
2
4) of
Rangul
termenului
care conţine
pe x . 2
4.The rank
the
term
that
contains
x².
4) Rangul termenului care conţine pe x .
5. How many
rational
terms
does
the
development has?
5) Câţi
termeni
raţionali
are
dezvoltarea?
5) Câţi termeni raţionali are dezvoltarea?
11










 mathematics
mathematics








