Similar presentations:
Приёмы преобразования графиков
1. Основные приёмы преобразования графиков
1.Преобразование симметрии относительно оси
абсцисс
2.
Преобразование симметрии относительно оси
ординат
3.
Параллельный перенос вдоль оси абсцисс
4.
Параллельный перенос вдоль оси ординат
5.
Растяжение и сжатие вдоль оси абсцисс
6.
Растяжение и сжатие вдоль оси ординат
7.
Построение графика функции у =│f(x)│
8.
Построение графика функции у = f(│x│)
9.
Построение графика функции у = │f(│x│)│
Содержание
2. f(x) → – f (x)
уf(x) → – f (x)
у f (x)
х
0
у f (x)
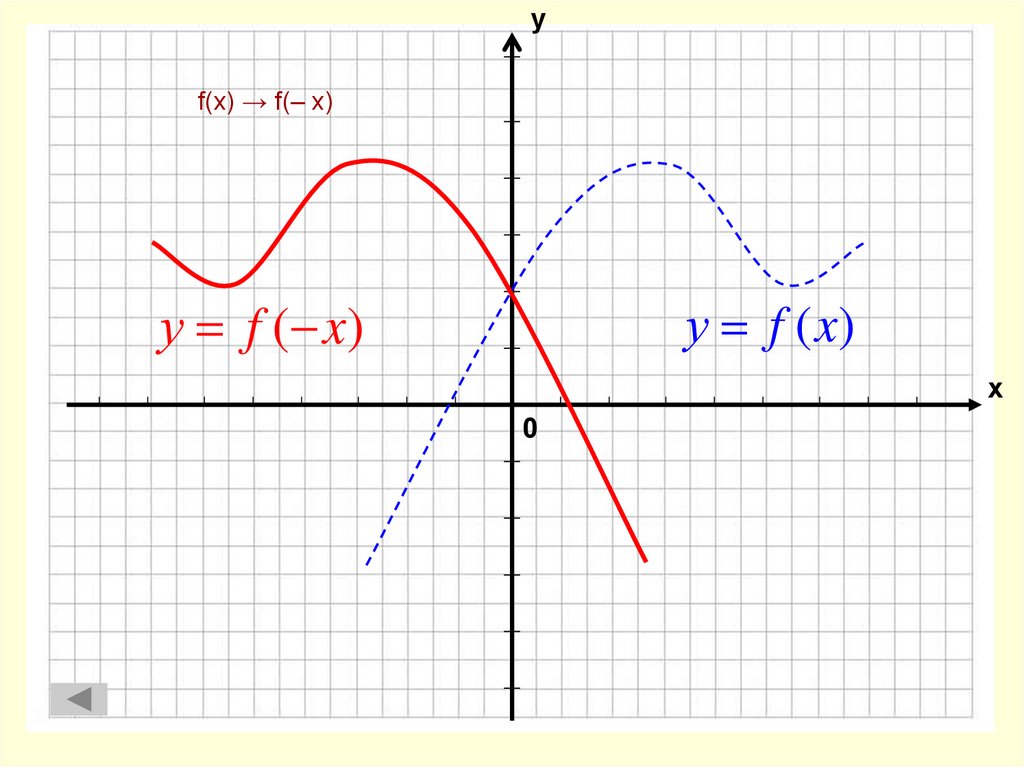
3. f(x) → f(– x)
уf(x) → f(– x)
у f ( x)
у f (x)
х
0
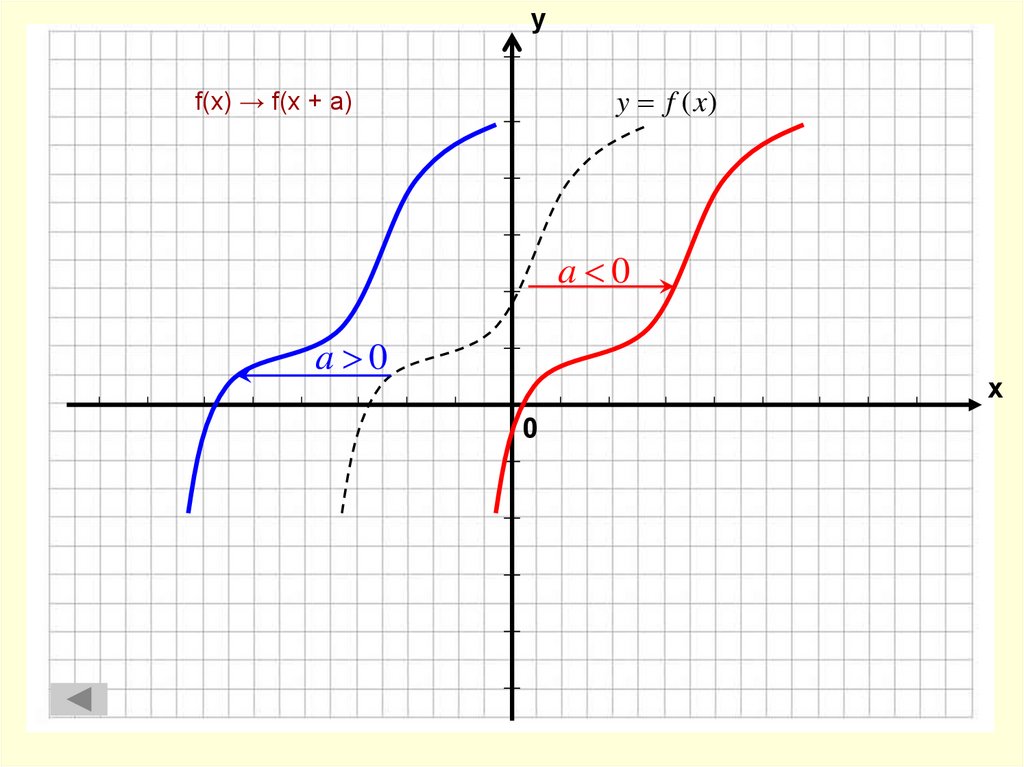
4. f(x) → f(x + а)
уy f (x)
f(x) → f(x + а)
a 0
a 0
х
0
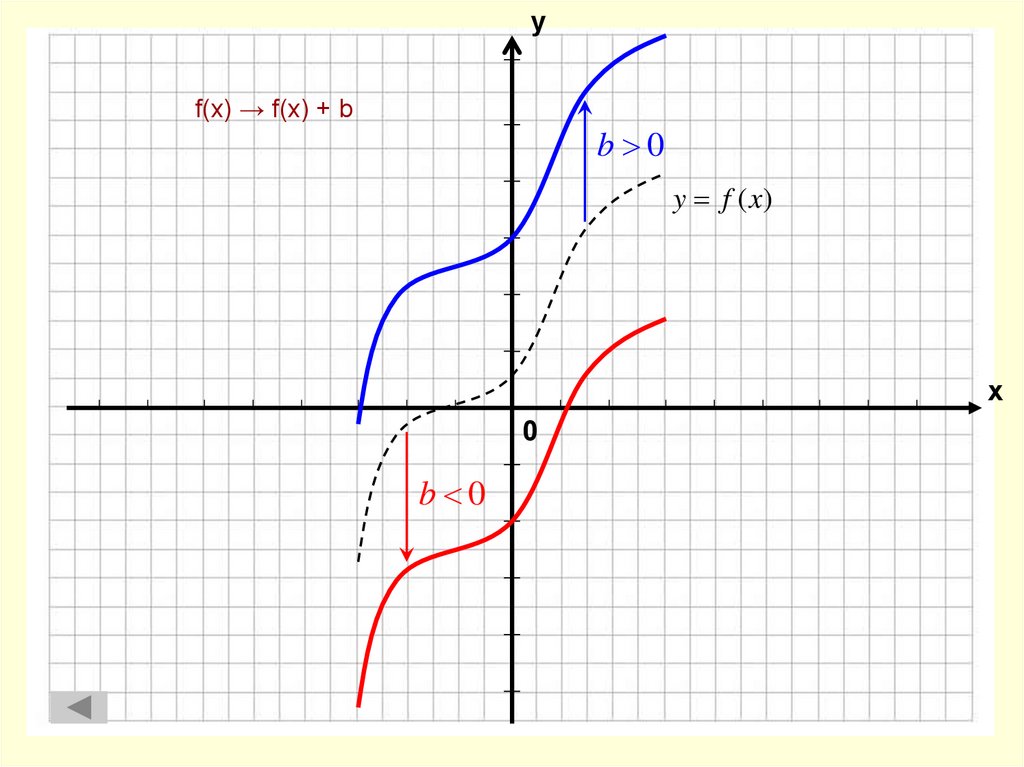
5. f(x) → f(x) + b
уf(x) → f(x) + b
b 0
y f (x)
х
0
b 0
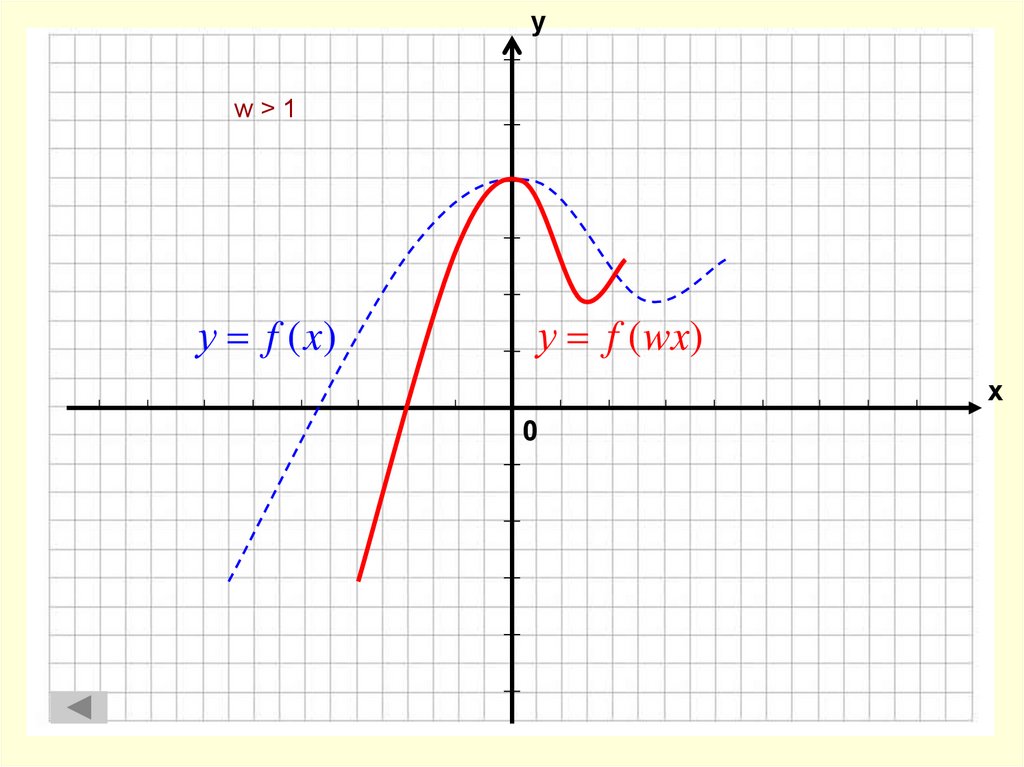
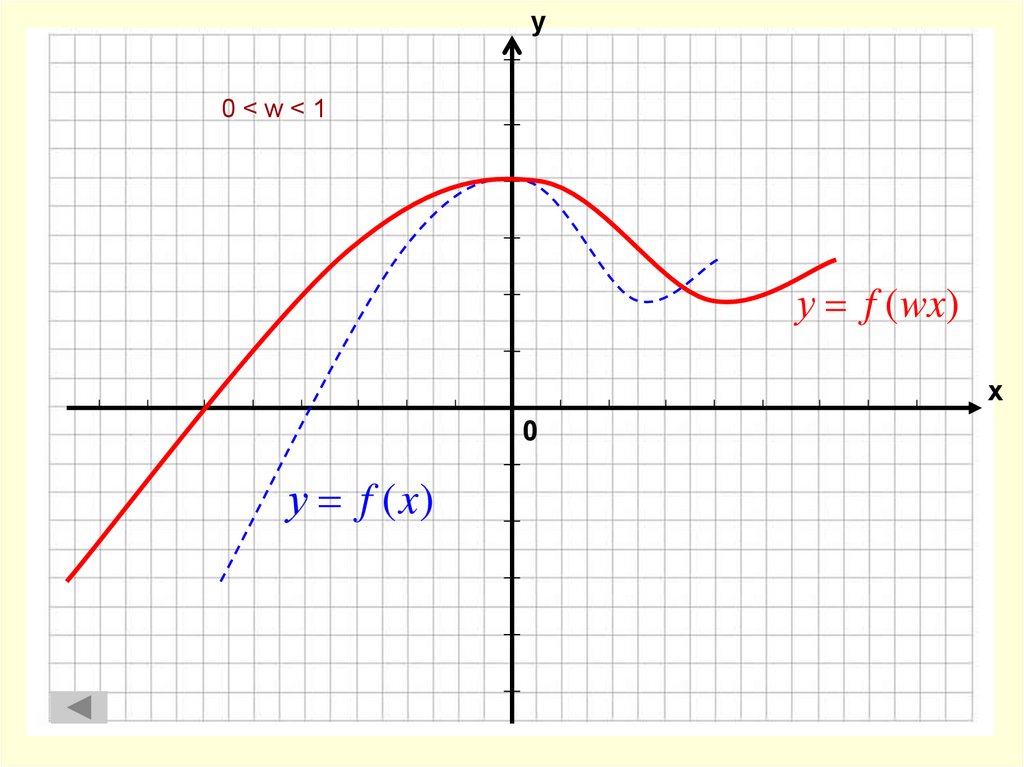
6. f(x) → f(wx)
1.2.
0<w<1
w>1
7. w > 1
уw>1
у f (wx)
у f (x)
х
0
8. 0 < w < 1
у0<w<1
у f (wx)
х
0
у f (x)
9.
f (x) kf (x), где k 01.
2.
k>1
0<k<1
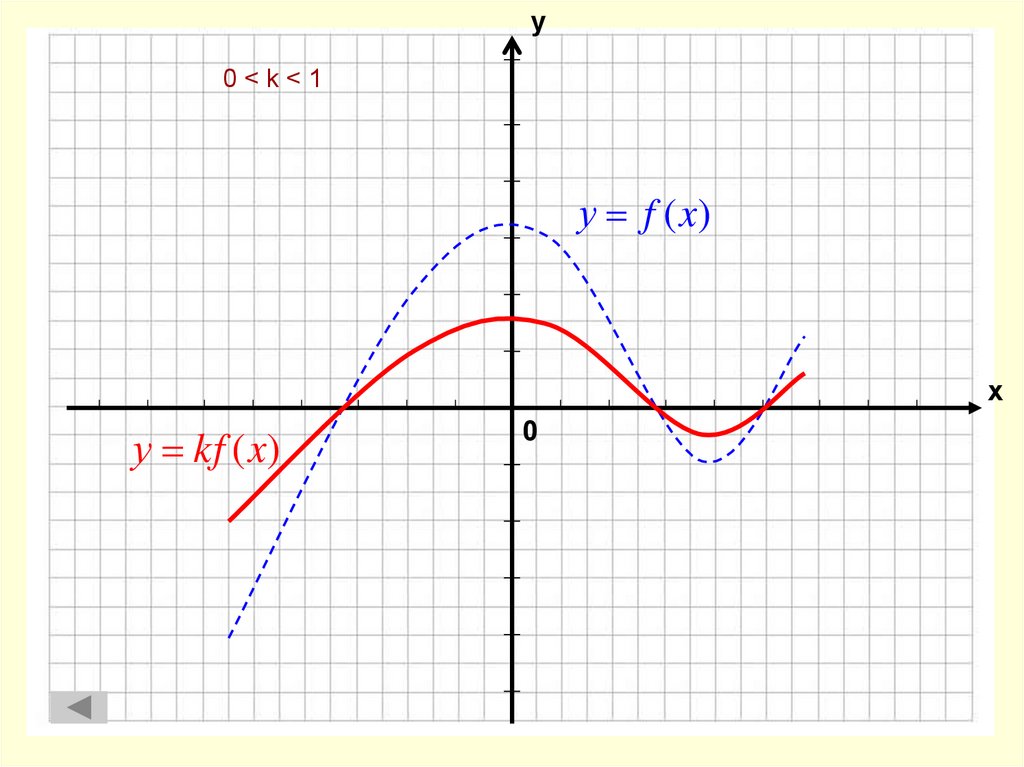
10. 0 < k < 1
у0<k<1
у f (x)
х
у kf (x)
0
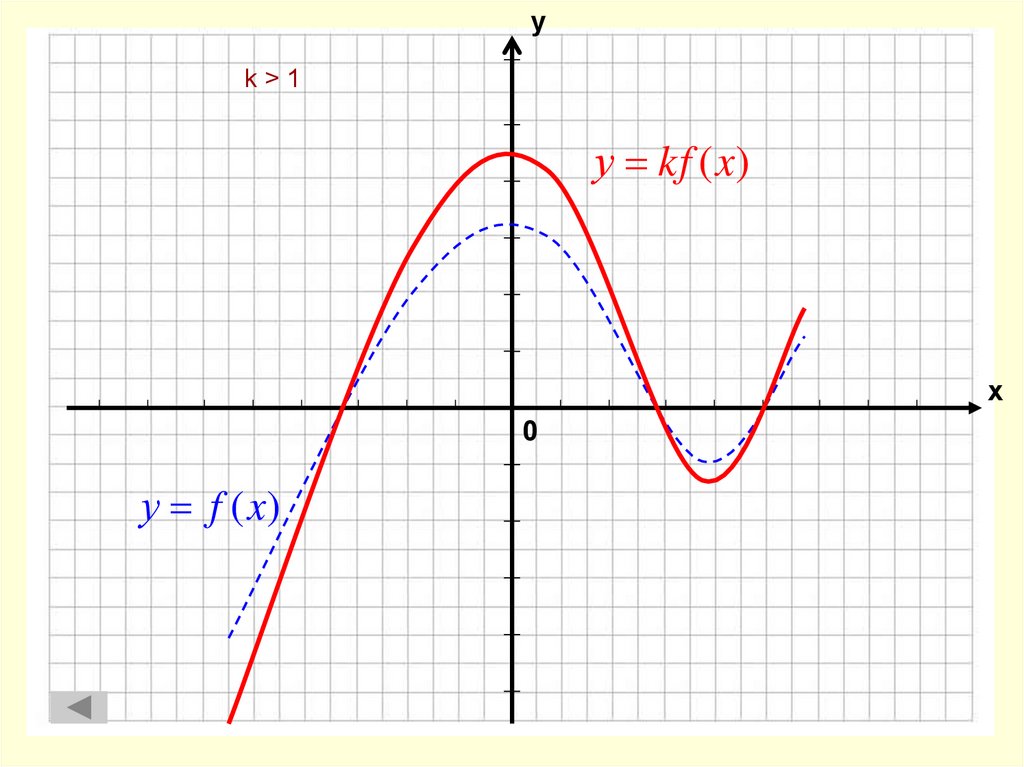
11. k > 1
уk>1
у kf (x)
х
0
у f (x)
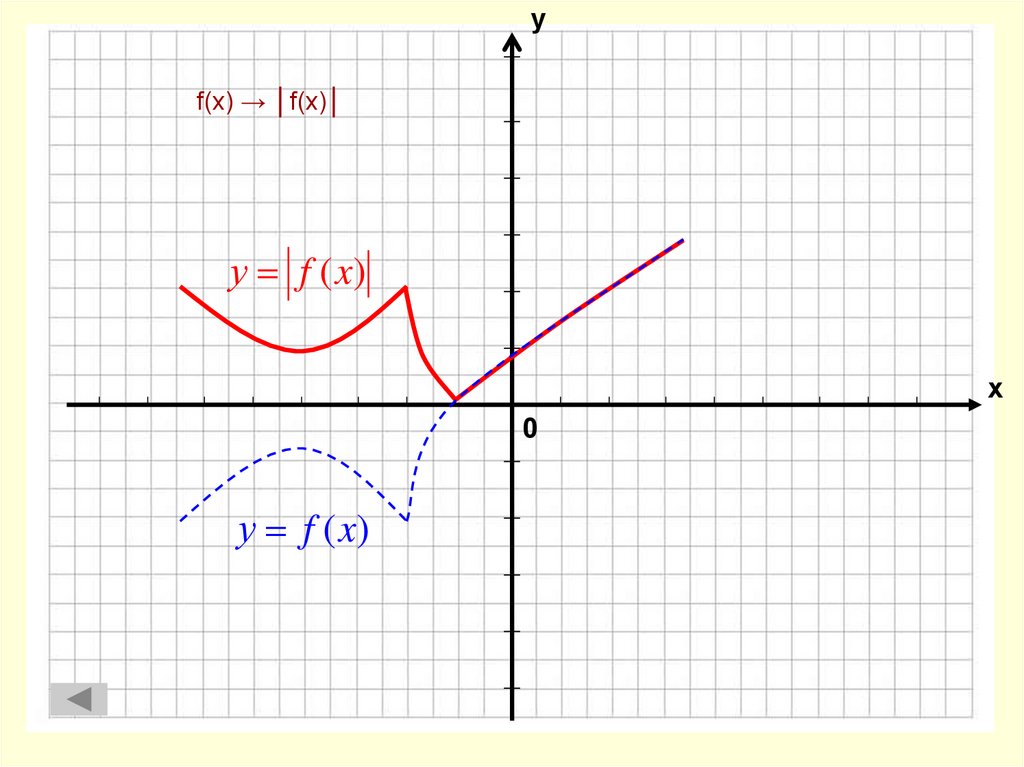
12. f(x) → │f(x)│
уf(x) → │f(x)│
у f (x)
х
0
у f (x)
13. f(x) → f(│x│)
уf(x) → f(│x│)
у f ( x)
х
0
у f (x)
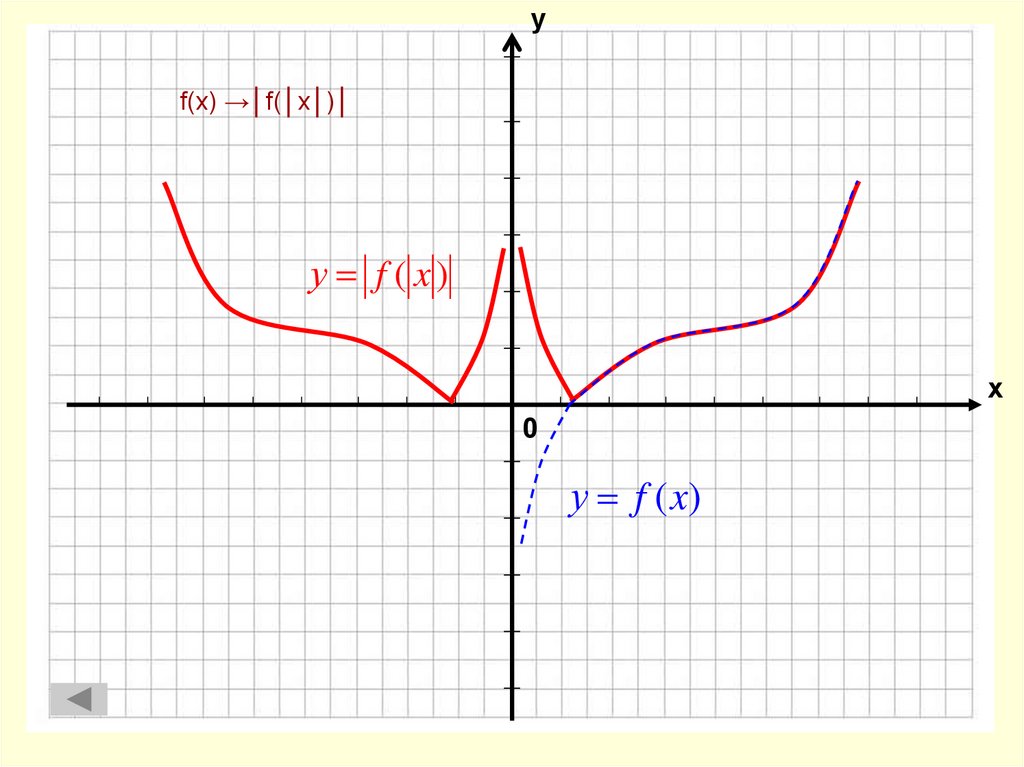
14. f(x) →│f(│x│)│
уf(x) →│f(│x│)│
у f ( x)
х
0
у f (x)
15. последовательныe преобразования графиков элементарных функций (на примерах)
1. y x 2 6 x 82. y 3 sin 2 x 1
x
3. y 2 sin x( )
3 6
Содержание
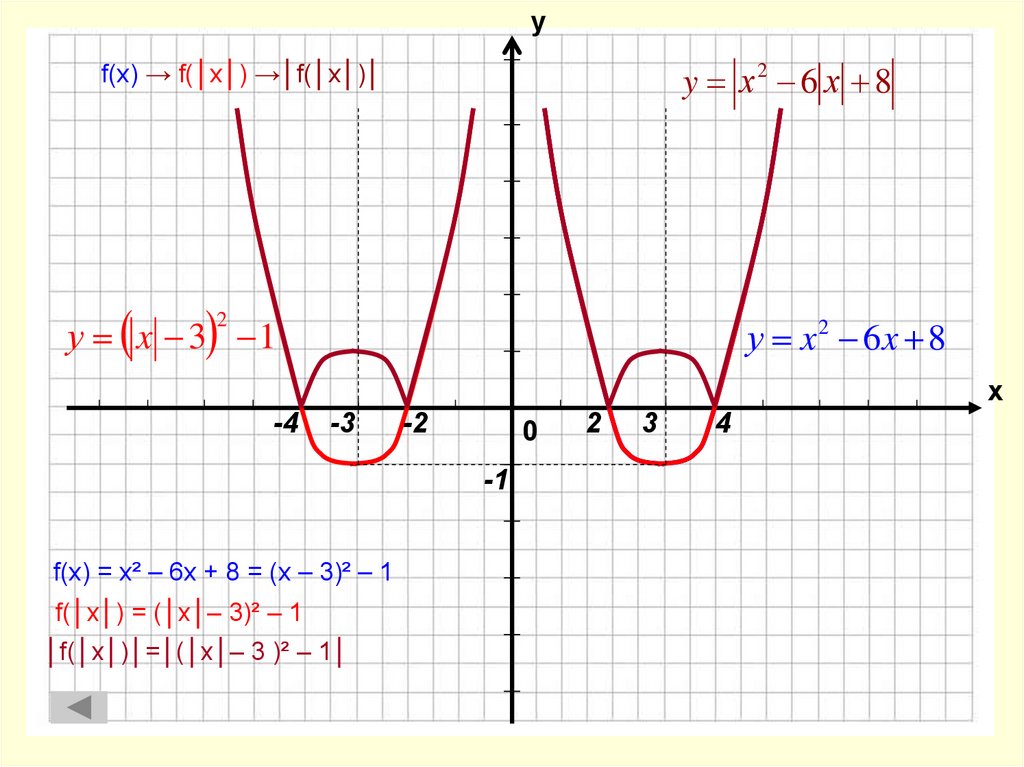
16. f(x) → f(│x│) →│f(│x│)│
1. f(x) = x² – 6x + 8 = (x – 3)² – 12. f(│x│) = (│x│– 3)² – 1
3. │f(│x│)│=│(│x│– 3)² – 1│
17. f(x) = x² – 6x + 8 = (x – 3)² – 1
уy х2 6 х 8
f(x) → f(│x│) →│f(│x│)│
у x 3 1
2
у x2 6x 8
х
-4
-3
-2
0
-1
f(x) = x² – 6x + 8 = (x – 3)² – 1
f(│x│) = (│x│– 3)² – 1
│f(│x│)│=│(│x│– 3 )² – 1│
2
3
4
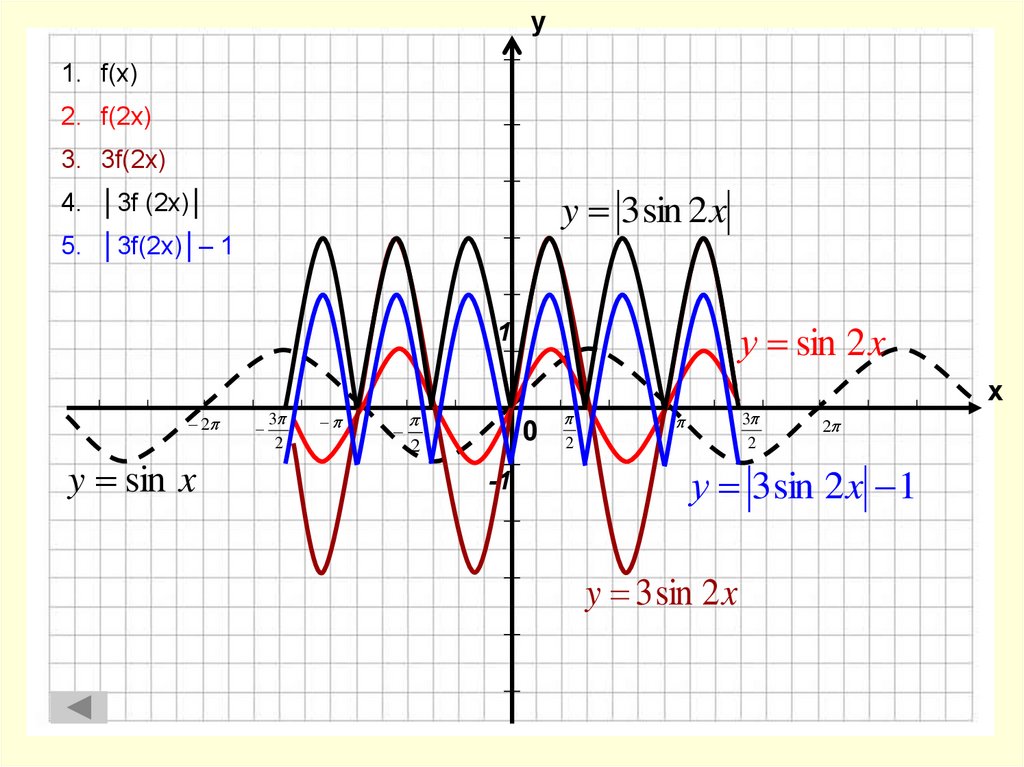
18.
у1. f(x)
2. f(2x)
3. 3f(2x)
y 3 sin 2 x
4. │3f (2x)│
5. │3f(2x)│– 1
у sin 2 x
1
2
y sin x
3
2
0
2
-1
3
2
2
х
2
у 3 sin 2 x 1
y 3 sin 2 x
19.
x1
y 2 sin( ) 2 sin( ( x ))
3 6
3
2
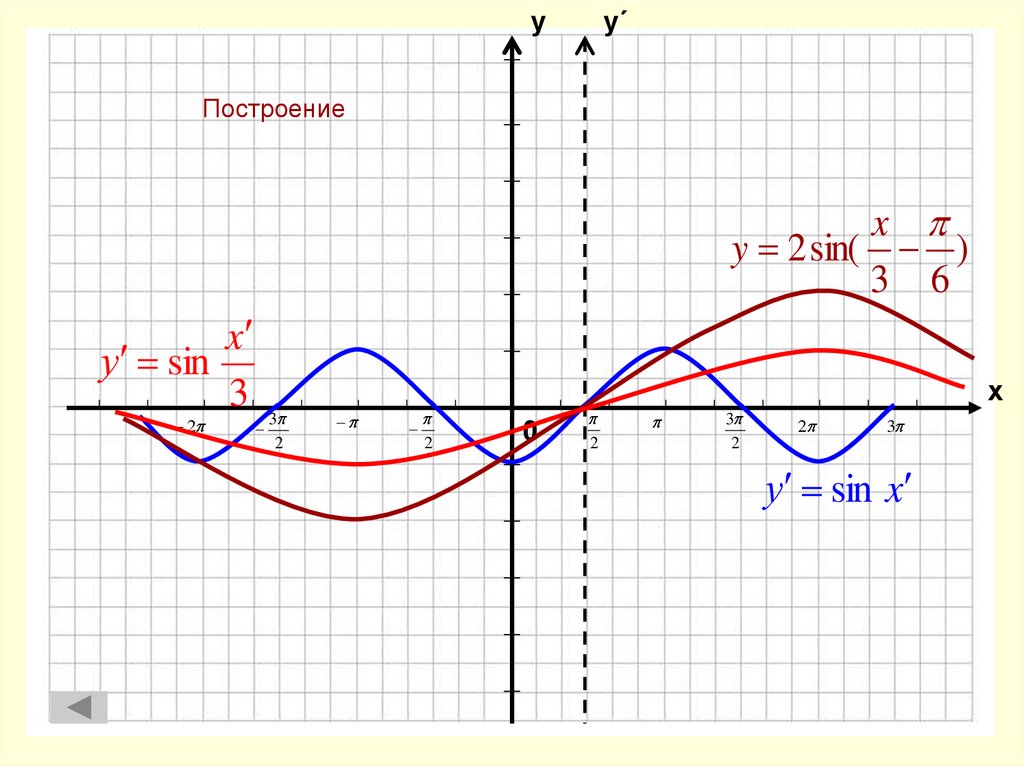
Этапы построения графика :
1. Осуществим параллельный перенос системы координат, поместив
начало новой системы x y в точку ( ; 0)
2
2. В новой системе строим график функции y sin x
3. Осуществив сжатие построенного графика к оси y с коэффициен том
1
,
3
1
получим y sin( x )
3
4. Осуществив растяжение последнего графика от оси х с коэффициен том 2,
получим требуемый график
20. Построение
уу΄
Построение
x
y 2 sin( )
3 6
x
у sin
3
2
3
2
2
0
2
3
2
х
2
3
у sin x
21. Проверь себя
1. х 22. х
3. sin x
4. cos x
5. a
Содержание
x
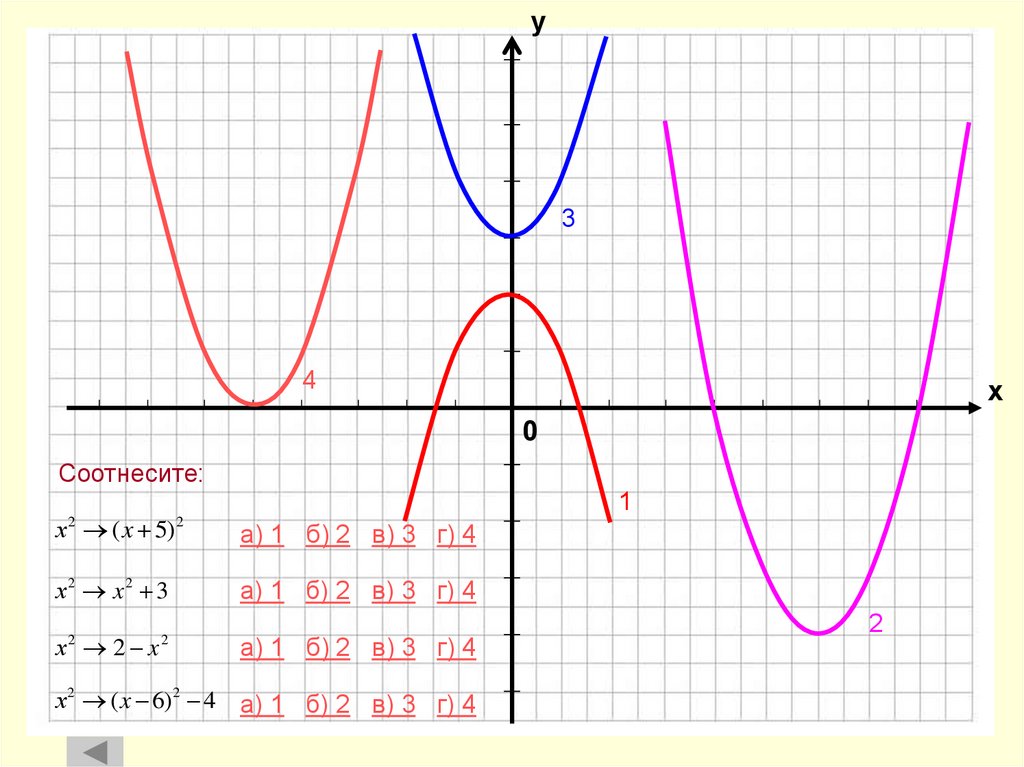
22. Соотнесите:
у3
4
х
0
Соотнесите:
х ( x 5)
2
1
2
х2 x2 3
х 2 x
2
2
х 2 ( x 6) 2 4
а) 1 б) 2 в) 3 г) 4
а) 1 б) 2 в) 3 г) 4
а) 1 б) 2 в) 3 г) 4
а) 1 б) 2 в) 3 г) 4
2
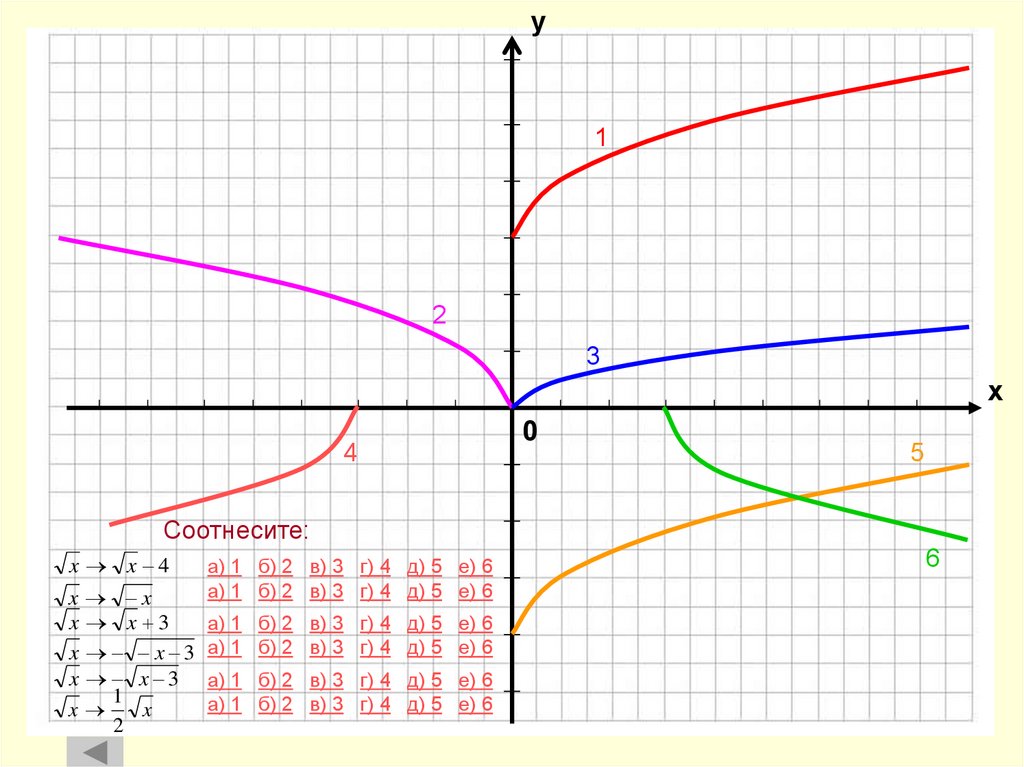
23. Соотнесите:
у1
2
3
х
4
0
5
Соотнесите:
x x 4
x
x
x
x
x
x
x 3
x 3
x 3
1
x
2
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
а) 1 б) 2 в) 3 г) 4 д) 5 е) 6
6
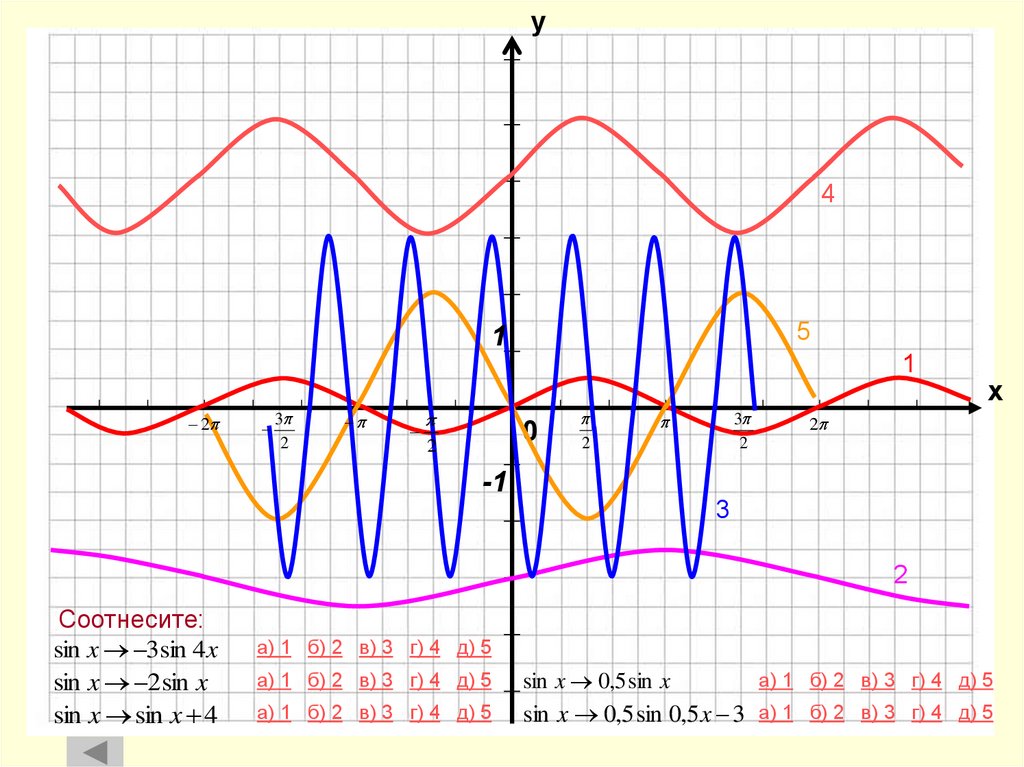
24. Соотнесите:
у4
5
1
1
2
3
2
0
2
2
3
2
х
2
-1
3
2
Соотнесите:
sin x 3sin 4x
sin x 2 sin x
sin x sin x 4
а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
sin x 0,5 sin x
а) 1 б) 2 в) 3 г) 4 д) 5
sin x 0,5 sin 0,5 x 3 а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
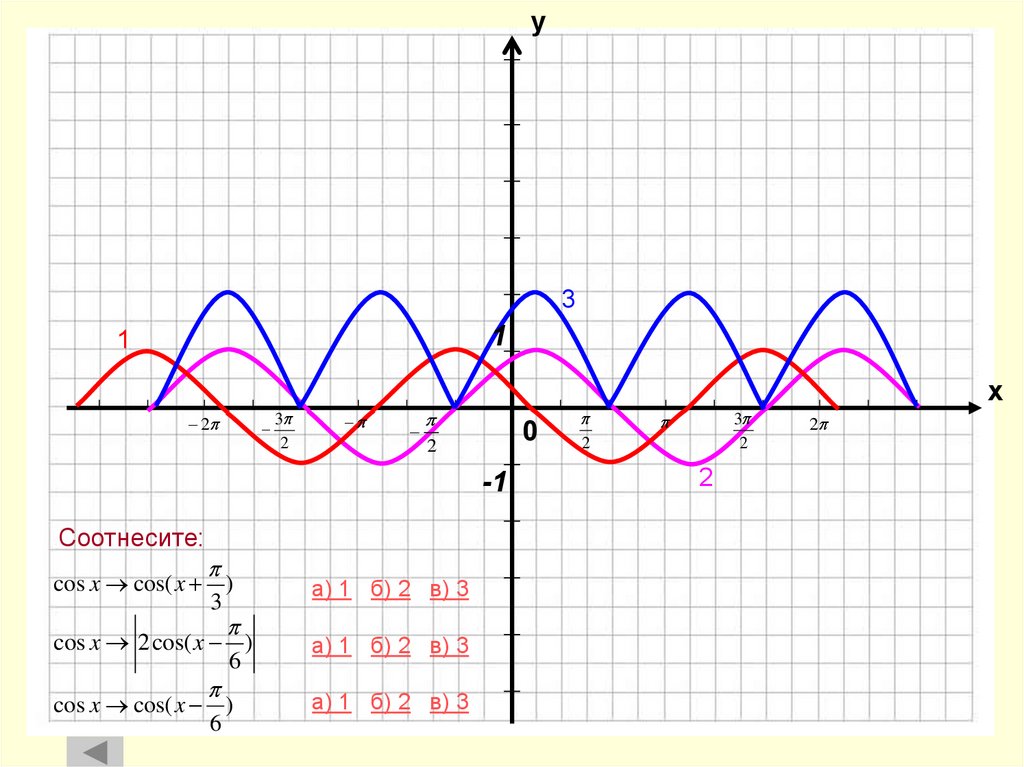
25. Соотнесите:
у3
1
1
2
3
2
0
2
-1
Соотнесите:
cos x cos( x )
3
а) 1 б) 2 в) 3
cos x 2 cos( x )
6
cos x cos( x )
6
а) 1 б) 2 в) 3
а) 1 б) 2 в) 3
2
3
2
2
х
2
26. Соотнесите:
у1
5
3
х
0
Соотнесите:
х 4
2 2
2 х 2 х 7 1
2 хх 2 хх 3
2 2
2 х 2 х
х
4
а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
а) 1 б) 2 в) 3 г) 4 д) 5
2
27. Всё!
28. Молодец!
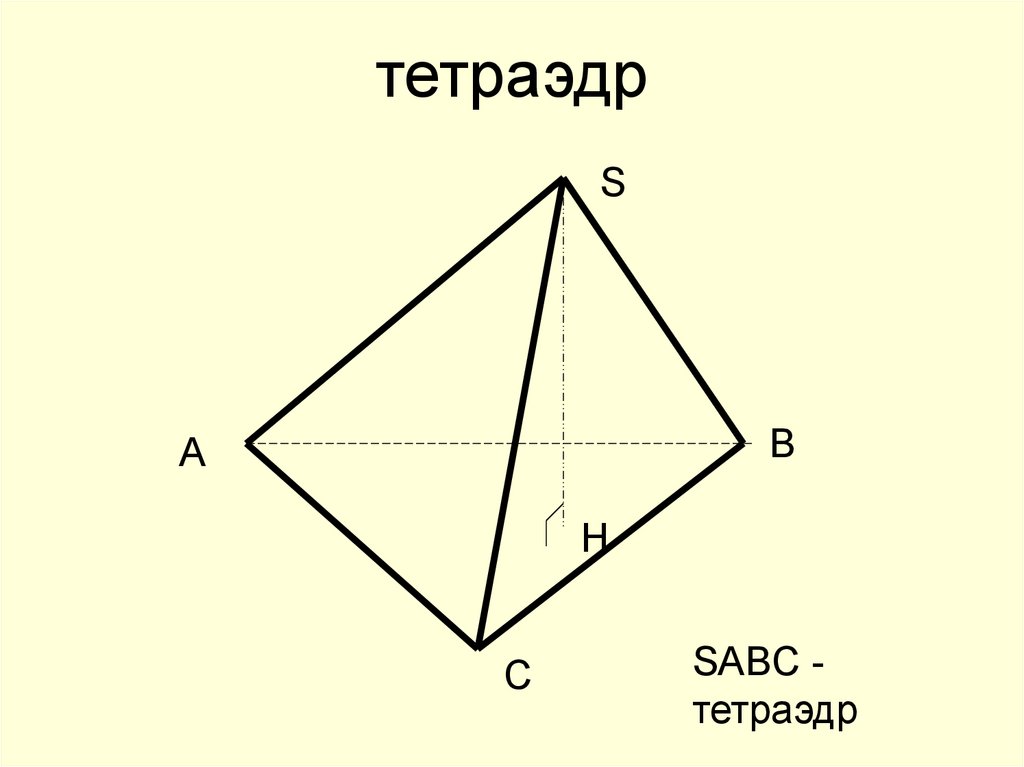
29. тетраэдр
SB
A
H
C
SABC тетраэдр
30. Кластер
Основание;
Ребра;
Вершины;
Грани;
Высоты.
31. На окраине Каира - столицы современного Египта самая высокая - пирамида Хеопса
32. Центральная Америка к северу от Мехико город Теотиукан
Пирамида Солнца33. остров Тенериф: Пирамиды Гуимар
34. На фоне Гималайского хребта четко выделяется пирамидальное образование – гора Кайлас
35. Стеклянная пирамида в Париже Новый вход в Лувр, высота 21,65метра
36.
• Франкфурт:загородный дом
1896 года. Одна из
башен имеет
форму пирамиды и
придает зданию
величавый вид.
37. Алгоритм
Определение.
Основание.
Боковая грань
Вершины.
Ребра.
Площадь боковой поверхности.
Площадь полной поверхности
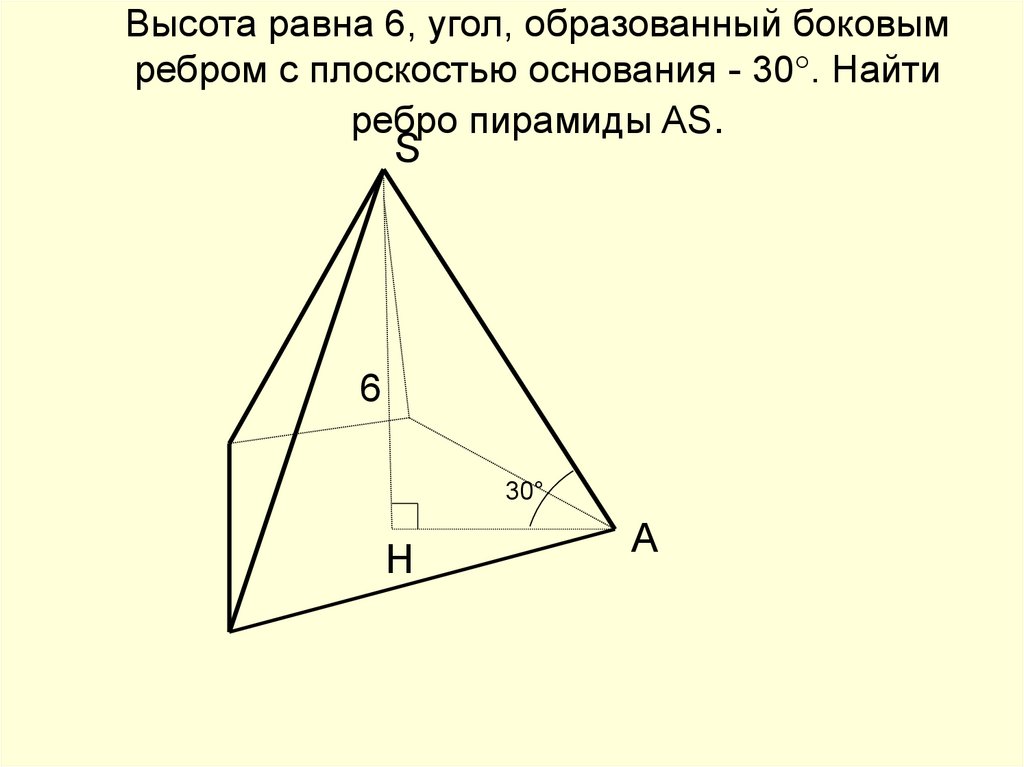
38. Высота равна 6, угол, образованный боковым ребром с плоскостью основания - 30°. Найти ребро пирамиды AS.
S6
30°
H
A
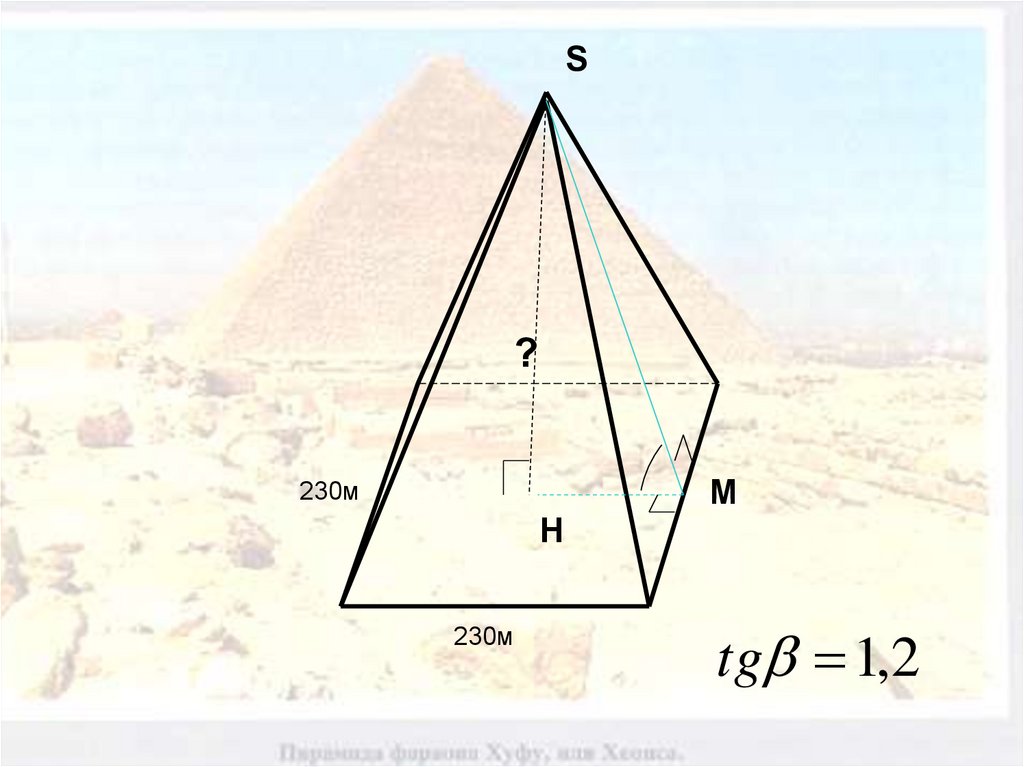
39.
S?
230м
M
H
230м
tg 1,2
40. Тест
• : Сколько граней, боковых ребер у n-угольнойпирамиды?
• Какое наименьшее число граней может иметь
пирамида?
• Высота пирамиды равна 3см. Чему равно
расстояние от вершины пирамиды до
плоскости основания?
• Боковые ребра треугольной пирамиды равны
7см, 12см, 5см. Одно из них перпендикулярно
к плоскости основания. Чему равна высота
пирамиды?
41. Применение компьютерных технологий на уроках математики :
• 1. Активизирует познавательнуюдеятельность
• 2. Формирует позитивное отношение к
предмету
• 3. Расширяет эрудицию и кругозор
• 4. Развивает творческие способности
• 5. Стимулирует умственную
деятельность



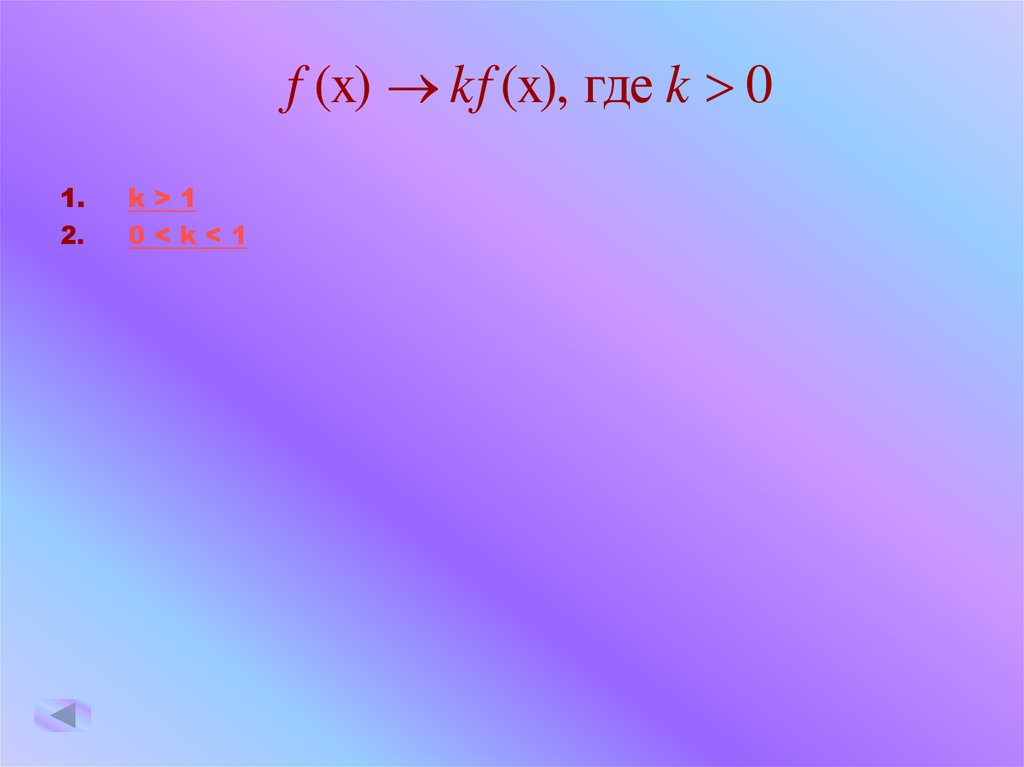


















 mathematics
mathematics








