Окружность. Задачи

1. Окружность.

Знаменская гимназия
Сергеенкова С.Ю.
Геометрия, 7 класс.

2.

1.
2.
Т
С
3.
А
4.
5.
О
6.
Н
В
7.
8.
9.
10.
Что такое окружность?
Что называют её центром?
Что такое радиус
окружности?
Что такое диаметр
окружности?
Что такое хорда
окружности?
Что называют дугой
окружности?
Назовите радиусы.
Назовите хорды.
Чему равен диаметр
окружности?
На какие дуги окружность
разбивают точки С и В?

3. Задача №1.

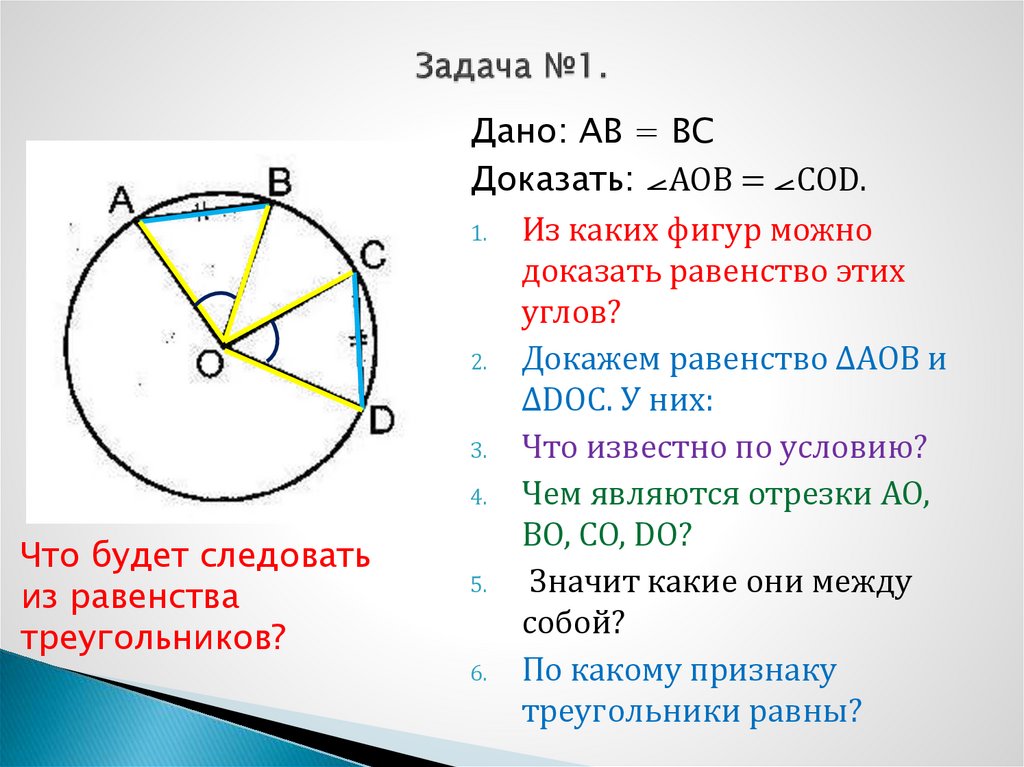
Что будет следовать
из равенства
треугольников?
Дано: АВ = ВС
Доказать: ⦟АОВ = ⦟СОD.
1. Из каких фигур можно
доказать равенство этих
углов?
2. Докажем равенство ∆АОВ и
∆DОС. У них:
3. Что известно по условию?
4. Чем являются отрезки АО,
ВО, СО, DО?
5.
Значит какие они между
собой?
6. По какому признаку
треугольники равны?

4. Задача №2.

Что следует из
равенства
треугольников?
Дано: ⦟MOP=⦟NOK
Доказать: MN=PK.
В какие фигуры входят эти отрезки?
Рассмотрим ∆MNO и ∆PKO. У них:
1. МО=NO=PO=KO, как радиусы
окружности.
Какого элемента в треугольниках
не хватает, чтобы говорить о их
равенстве?
2. Так как ⦟MOP=⦟NOK и ⦟NOP –
часть каждого из этих углов, то
оставшиеся части данных углов тоже
равны, т.е. ⦟MON=⦟POK.
По какому признаку треугольники
равны?

5. Задача №3.

Дано: АВ =CD, Е – середина АВ,
F- середина CD
Доказать: ОЕ = ОF.
Равенство отрезков можно взять
из равных треугольников. Как их
получить?
Рассмотрим ∆DОС и ∆АОВ.
У них: АВ = СD(по условию),
АО=ВО=СО=DО как радиусы.
⇒ ∆DОС = ∆АОВ по трём
сторонам. Из равенства⇒
Так как Е и F – середины сторон,
то ЕА=СF и ⦟А=⦟С, то ∆АОЕ = ∆COF
по двум сторонам и углу между ними.
⇒ ОЕ = ОF.
Ч.т.д.