Similar presentations:
Задания республиканской олимпиады по математике для обучающихся по программам подготовки квалифицированных рабочих, служащих
1. Задания республиканской олимпиады по математике для обучающихся ПО ПРОГРАММАМ ПОДГОТОВКИ КВАЛИФИЦИРОВАННЫХ РАБОЧИХ, СЛУЖАЩИХ и
ПО ПРОГРАММАМ ПОДГОТОВКИСПЕЦИАЛИСТОВ СРЕДНЕГО ЗВЕНА
в профессиональных
образовательных
организациях
Республики Башкортостан
2.
Олимпиадные задания по математике1. Творческий характер.
2. Умения и знания разделов общеобразовательной
дисциплины «Математика».
3. Различная сложность.
3. Дисциплина «Математика»
I. Алгебра:Корни, степени и логарифмы.
Уравнения и неравенств (иррациональные, показательные,
логарифмические, тригонометрические).
Функции, свойства функций.
II. Начала математического анализа:
Теория пределов.
Дифференциальное исчисление.
Интегральное исчисление.
4. Дисциплина «Математика»
III. Геометрия:Планиметрия.
Стереометрия.
Многогранники.
Тела вращения.
IV. Теория вероятностей и математическая статистика:
Комбинаторика.
Теория вероятностей.
Математическая статистика.
5.
Примерные задания по математике дляобучающихся по программам
подготовки специалистов среднего
звена в ПОО РБ
6.
Для определения эффективной температуры звезд используют законСтефана-Больцмана, согласно которому мощность излучения Р (в ваттах)
нагретого тела прямо пропорциональна площади его поверхности и
четвертой степени температуры: P ST 4 , где 5,7 10 8- постоянная,
площадь поверхности S измеряется в квадратных метрах, а температура Т –
в кельвинах. Известно, что некоторая звезда имеет площадь поверхности
1
27
S 1021 м 2
4,104
10
Вт .
,
а
излучаемая
его
мощность
Р
равна
18
Определите температуру этой звезды. Ответ дайте в кельвинах.
7.
15, 7 10 ; S 1021 м 2 Р 4,104 1027 Вт
18
8
Р
P ST T
Т 4 Р
S
S
4
4
4,104 1027
Т
4
8 1
5, 7 10 1021
18
18 4,104
1027
18 4,104
1027
4
8 21 4
8 21
5,7
10 10
5,7
10 10
27
24
24
18
4,104
10
6
4104
10
10
4
9 21 4
9 21 4 6 216 9 21
57
10 10
19
10 10
10 10
4 64 1012 6 103 6000К
8.
На полке в почвенной лаборатории случайно смешаны бюксы с различнымиобразцами почвы: 8 бюксов с влажной почвой и 6 - с сухой. Найти
вероятность того, что три из пяти наудачу взятых с этой полки бюксов будут
с сухой почвой.
14!
п С
2002
5! 9!
5
14
т С С
3
6
2
8
т С63 С82 560
р( А)
0, 2797
5
п
С14
2002
9.
Решите неравенствоlog2 x x 2 log x 3 3 x 0
х 2 0
x 2
3 x 0
x 3
2 x 1
x 1
ОДЗ: x 2;1 1;2
ОДЗ :
;
2 x 0
x 2
x 3 1
x 3
x 3 0
x 3
Применим метод декомпозиции
logh f log p g 0 h 1 f 1 p 1 g 1 0
2 х 1 х 2 1 х 3 1 3 х 1 0
х 1 х 1 х 2 х 2 0
х 2; 1 1; 2
10.
Решите уравнение3
53х 9 6х 4 3 61,5 х 9 3 4 62 х 4 52 х 4 5х
5х 3 6
5
х 3
х
2
2
5
х 2
6
х
3
2
3 6
5 6
х
х
3
2
6
125 5х 25 5х 5х 36 6
х
1
2
х
1
2
х
1
2
х
1
2
5х 2 5х
х
2
2
3 6
6 6
х
1
2
99 5 33 6 ; 3 5 6 ; lg3 5 lg 6
х
х
х
lg 3 x lg 5 1 lg 6;
2
х
x lg 5 lg 6 lg 6 lg 3;
2
х
х
1
2
3 6
х
1
2
х
lg 3 x lg 5 lg 6 lg 6
2
lg 2
х
lg 5 lg 6
х
1
2
11.
Предприятие запланировало за два года увеличить объем продукции в 2,89раза. Каким (в процентах) должен быть годовой прирост продукции, если он
одинаков для каждого года?
.
1. Пусть прирост продукции за год равен
первоначальный годовой объем производства А.
х%,
2. Тогда через год объем производства должен составить
100% х% А 1 0,01х А , а через два года
100% х% 1 0, 01х А 1 0, 01х
2
А
3. Этот объем равен 2,89А, а потому 1 0, 01х 2,89
2
.
Отсюда 1 0, 01х 1, 7
ОТВЕТ: 70%
х 0, 7
а
12.
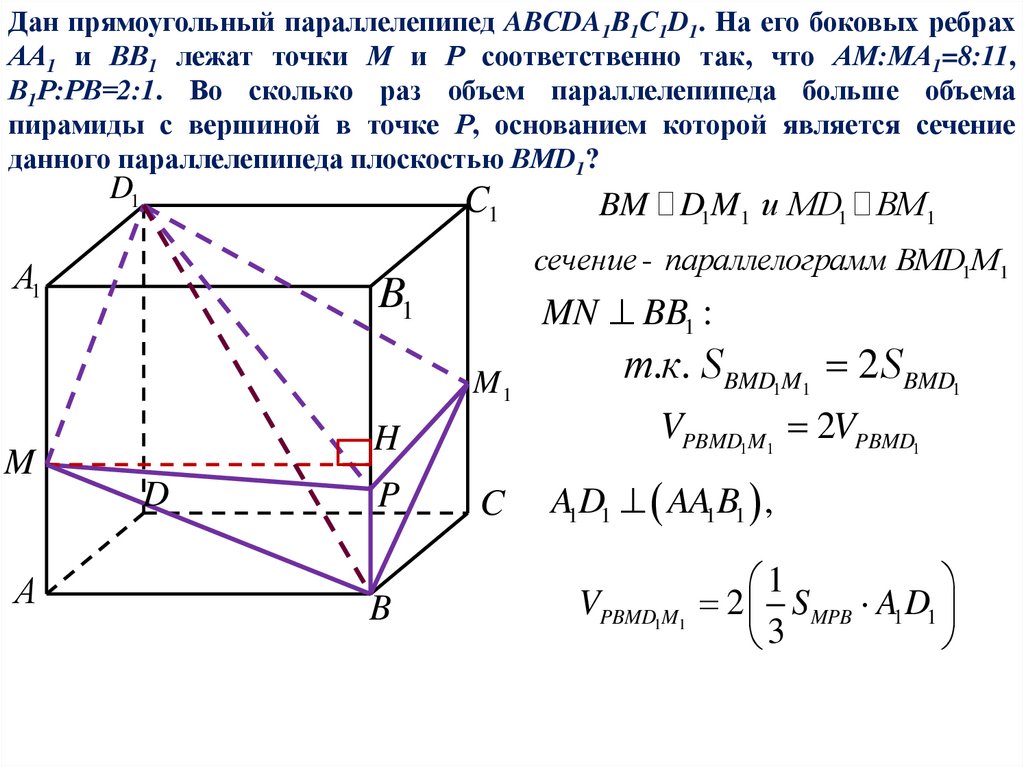
Дан прямоугольный параллелепипед ABCDA1B1C1D1. На его боковых ребрахАА1 и ВВ1 лежат точки М и Р соответственно так, что АМ:МА1=8:11,
В1Р:РВ=2:1. Во сколько раз объем параллелепипеда больше объема
пирамиды с вершиной в точке Р, основанием которой является сечение
данного параллелепипеда плоскостью ВМD1?
D1
C1
А1
cечение - параллелограмм BMD1M1
B1
MN BB1 :
M1
M
А
H
D
P
B
BM D1M1 и MD1 BM1
C
т.к. S BMD1M1 2S BMD1
VPBMD1M1 2VPBMD1
A1D1 AA1B1 ,
VPBMD1M1
1
2 S MPB A1D1
3
13.
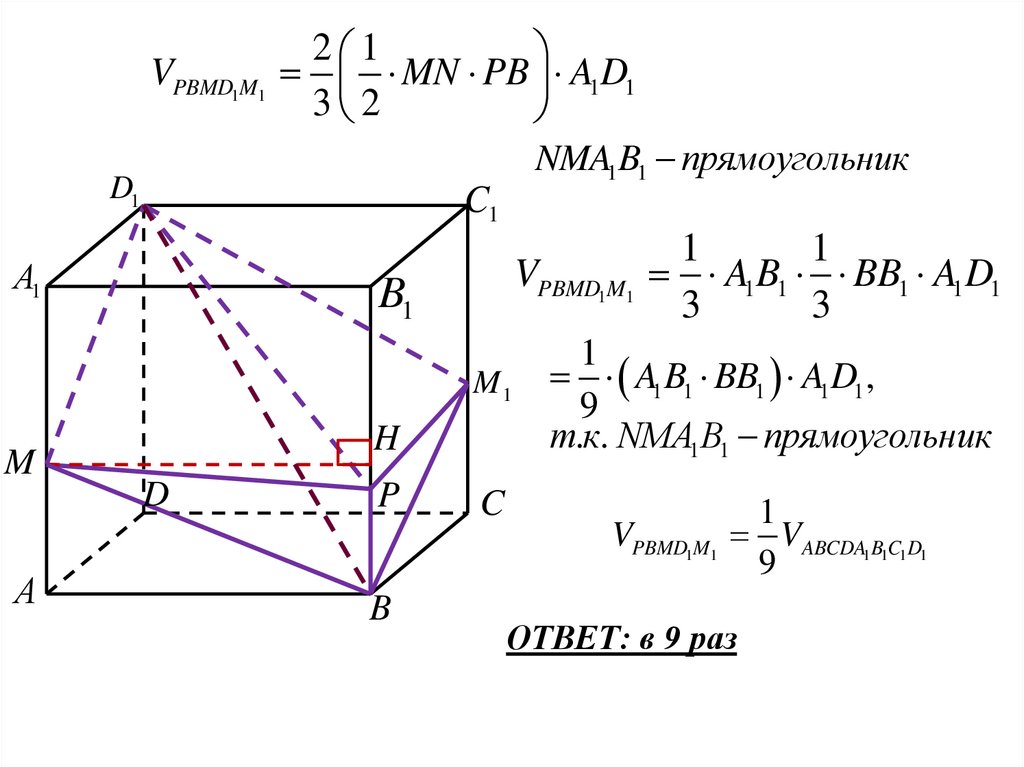
VPBMD1M12 1
MN PB A1D1
3 2
NMA1B1 прямоугольник
D1
C1
А1
VPBMD1M1
B1
M1
M
А
H
D
P
B
C
1
1
A1 B1 BB1 A1D1
3
3
1
A1B1 BB1 A1D1 ,
9
т.к. NMA1B1 прямоугольник
VPBMD1M1
1
VABCDA1B1C1D1
9
ОТВЕТ: в 9 раз
14.
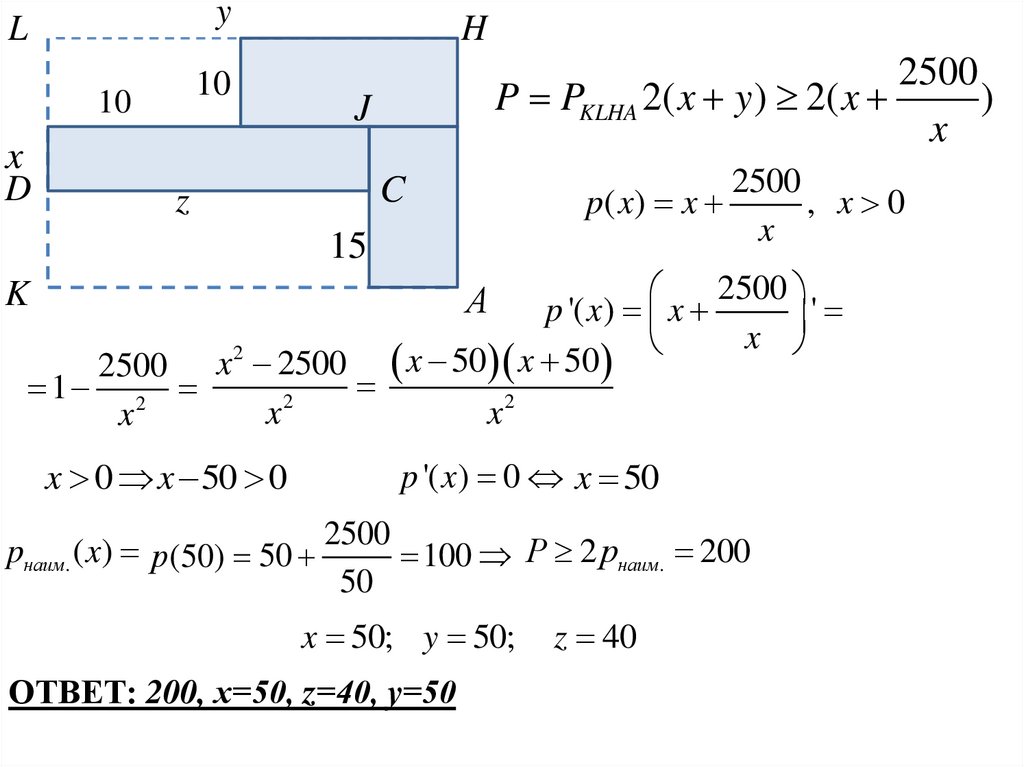
Требуется разметить на земле участок ABCDEFGH площадью 1800 м2,состоящий из трех прямоугольных частей и имеющий форму, изображенную
на рисунке, где FG=EF=10м, ВС=15м и CD 40м. Найдите наименьшее
значение периметра такого участка и какие-либо значения длин KL, LH и
CD, при которых периметр является наименьшим.
y
L
E
x
D
K
10
G
10
F
H
J
I
1. Пусть KL=х, LH=y, CD=z. Тогда
z≥40 и площадь прямоугольника KLHA
z
C
15
B
равна
А
xy 1800 10 10 15 z 1800 10 10 15 40
y
2500
x
15.
yL
10
10
x
D
H
2500
P PKLHA 2( x y ) 2( x
)
x
J
2500
p ( x) x
, x 0
x
C
z
15
K
2500
p '( x) x
'
x
x 50 x 50
А
2
2500 x 2500
1 2
2
x
x
x2
x 0 x 50 0
p '( x) 0 x 50
pнаим. ( x) р (50) 50
2500
100 Р 2 pнаим. 200
50
x 50; y 50;
ОТВЕТ: 200, х=50, z=40, у=50
z 40
16.
yL
10
10
x
D
H
J
KL x, LH y, CD 40 d
(d 0)
xy 1800 10 10 15(40 d )
C
z
15
K
А
2500 15d
2500 15d y
x
250015d
P 2 x y 2 x
x
x 50 2 15d x 50
2
100 200
x
pнаим. 200
d 0 x y 50
x 50; y 50;
ОТВЕТ: 200, х=50, z=40, у=50
z 40
17.
При каких значениях а сумма log cos 2 x 1a
и
log a cos 2 x 5
равна 1 хотя бы при одном значении х?
1. log a cos 2 x 1 log a cos 2 x 5 1
loga c 1 c 5 loga a
c 1 c 5 a 0 a 1, т.к. c 0
2
c 2 6c 5 a c 3 4 a
2. E cos x 1;1
E(c) 0;1 E(c 3) 3;4 E c 3 9;16
2
E c 3 4 5;12
2
5 а 12
18.
Примерные задания по математике дляобучающихся по программам
подготовки квалифицированных
рабочих, служащих в ПОО РБ
19.
11
а 1
: 1 а 1
а а 1
а а 1
а
а а 1
а 1
: 1
а 1
а 1
а а 1
:
а а 1
а а 1
а а 1
а а 1
а а 1 а 1 а 1
:
а а 1
а 1
а а 1
а а 1 а а 1
а 1 а 1
а 1
а 1
а 1 а 1
а 1
а 1 а 1
20.
Цена некоторого товара снижается ежегодно на 10%. На сколько процентовпо сравнению с первоначальной снизится стоимость товара через четыре
года?
.
1. Снижение цены за первый год на 10% означает, что она
составит 90%=0,9 начальной стоимости.
2. Воспользуемся формулой сложных процентов
3. Через четыре года стоимость товара будет равна
0,94 0,6561 65,61% первоначальной стоимость , а это
на 34,39% ниже.
ОТВЕТ: 34,39%
21.
В зрительном зале забронировано 10 мест для приглашенных гостей.Пришли 7 приглашенных. Найти вероятность того, что четверо из
пришедших гостей займут определенные для каждого из них места, если
гости занимают места случайным образом.
п А 10 9 8 7 6 5 4
7
10
т А 6 5 4
3
6
т А63
6 5 4
1
р( А) 7
п А10 10 9 8 7 6 5 4 5040
ОТВЕТ: 1/5040
22.
Найдите значение функцииf ( x) 10
x3 3 x
lg
log 0,1 x 5
x 5
в точке максимума.
f ( x) 10
x3 3 x
lg
log 0,1 x 5
x 5
lg x3 3 x
f ( x) 10
x3 3x
0
D( f ) : x 5
x 5 0
f ( x) 10
x3 3 x
lg
lg x 5
x 5
f ( x) x 3 x
3
2
x
3 x 0
D( f ) : x 3;
x 5
f '( x) x3 3x ' 3x 2 3 3 x 1 x 1
23.
f '( x) x3 3x ' 3x 2 3 3 x 1 x 1x
1
1 D f
x 1 единственная точка максимума
f ( 1) 1 3 1 2
3
ОТВЕТ:
1
2
24.
Решите уравнение7tgx cos2 x 3sin 2 x 1
sin x
7
3 2sin x cos x 1 cos 2 x
cos x
sin x
7
3 2sin x cos x sin 2 x 0
cos x
sin x
2
7
6
cos
x sin x cos x 0
cos x
sin x
0 tgx 0 x n, n Z
cos x
7 6 cos 2 x sin x cos x 0
sin x cos x 1
7 6 cos 2 x 7
ОТВЕТ: x n, n Z
7 1
25.
5Решите неравенство:
324 х 3 16
24 х 3 2
2 x 1
x
2 2 x 1
x
y 2t возрастает на D( y )
2 2 x 1
4х 3
x
4x 2
0
4 х 3
x
4 x 2 3x 4 x 2
0
x
x 2 4 x 1 0
x
4 x2 7 x 2
0
x
0, 25
ОТВЕТ: x ; 0, 25 0;2
0
2
x
26.
В прямоугольном параллелепипеде АВСDA1B1C1D1 известны длины ребер:АВ=3, AD=4, AA1=32. Найдите площадь сечения, проходящего через
вершины С, С1 и А
Сечением,
проходящим
через
D1
C1
А1
B1
вершины С, С1 и А является
прямоугольник.
Площадь
прямоугольника
равна
произведению его сторон.
По теореме Пифагора
D
А
C
B
ОТВЕТ: 160
AC AD 2 AB 2
42 32 5
SCC1 A1 A 5 32 160
27.
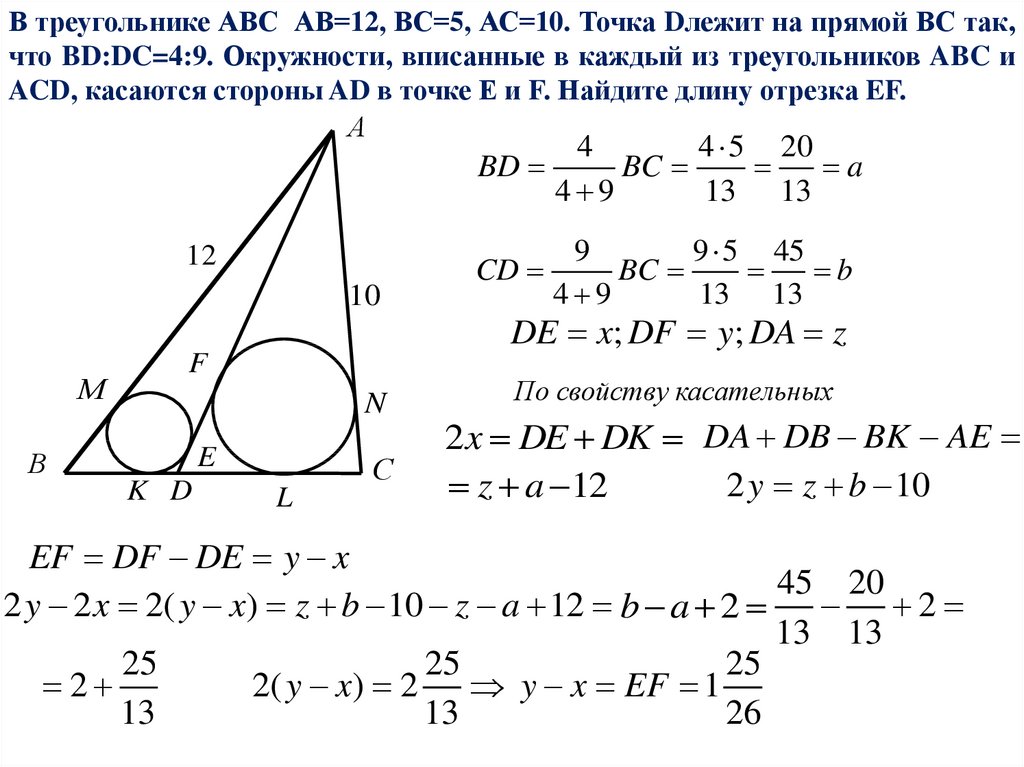
В треугольнике АВС АВ=12, ВС=5, АС=10. Точка Dлежит на прямой ВС так,что BD:DC=4:9. Окружности, вписанные в каждый из треугольников ABC и
ACD, касаются стороны AD в точке Е и F. Найдите длину отрезка EF.
А
4
4 5 20
BD
BC
a
4 9
13 13
12
10
М
F
N
E
В
K D
С
L
9
9 5 45
CD
BC
b
4 9
13 13
DE x; DF y; DA z
По свойству касательных
2x DE DK DA DB BK AE
2 y z b 10
z a 12
EF DF DE y x
45 20
2
2 y 2 x 2( y x) z b 10 z a 12 b a 2
13 13
25
25
25
2( y x) 2 y x EF 1
2
13
26
13
28.
СПАСИБОЗА
ВНИМАНИЕ !
29. Выступление на тему: «Решение задач повышенной сложности»
Хакимьянова Г.ГУфимский колледж радиоэлектроники,
телекоммуникаций и безопасности
преподаватель физики
30.
Задачи для олимпиадыподбираются так, чтобы дать
возможность студенту показать
знание курса физики в пределах
программы среднего
профессионального образования
на базе основного общего
образования, понимание
физических явлений и умение
правильно применять законы
физики для решения поставленных
задач.
.
31. Задача на закон всемирного тяготения
На какую часть ΔР уменьшаетсявес тела на экваторе вследствие
вращения Земли вокруг оси?
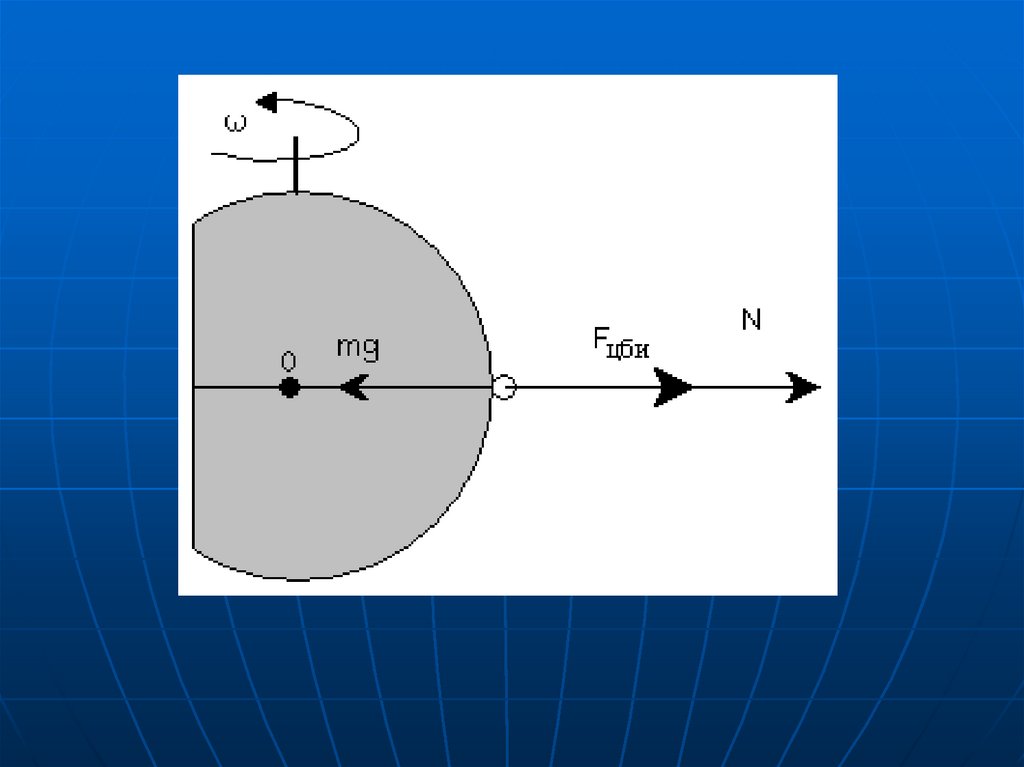
32. Решение
На тело, находящееся на экваторе, внеинерциальной системе отсчета
действуют следующие силы: сила
тяжести mg, сила реакции опоры N и
центробежная сила инерции Fцби
( рис.1). Причем, их сумма равна нулю.
Проецируя эти силы на радиальное
направление, получим уравнение:
N + Fцби = mg, откуда mg─ N= Fцби
33.
Рис. 134.
От сюда видно, что доля уменьшениявеса тела на экваторе равна:
ΔР/Р = 1─ N/mg = Fцби /mg = ω2 R/g, где
R – радиус Земли, ω – угловая скорость
вращения Земли. Подставляя
численные данные, получим: ΔР/Р =
3,4·10-3.
Итак, любое тело на экваторе
уменьшает свой вес вследствие
вращения Земли вокруг оси на 0,34%.
35. Задача на влажность воздуха
В запаянной трубке объемомV = 0,4л находится водяной пар
под давлением рп =8,5 ·103 Па при
температуре Tп = 423К. Какое
количество росы выпадет на
стенках трубки при ее охлаждении
до температуры Tнп = 295К?
36. Решение
В задаче рассматривают двасостояния пара в запаянной трубке – до
и после охлаждения. В первом
состоянии при его изохорном
охлаждении, начиная с некоторой
температуры (точки росы), пар станет
насыщающим, и дальнейшее понижение
температуры до 295 К вызовет его
частичную конденсацию.
37.
Происходит ли конденсация парапри изохорном понижении температуры
от значения T1 до T2 , если об этом не
сказано в условии задачи, можно
установить самим, зная плотность или
давление пара. С помощью таблиц
нужно только определить, будет ли
точка росы Тр > Т2 или нет. В данном
случае это неравенство имеет место,
следовательно, пар частично
конденсируется.
38.
Чтобы определить количество росы,выпавшей на стенках трубки, необходимо
найти массу пара при каждой из заданных
температур и вычесть из первого
результата второй. Для нахождения самих
масс удобно воспользоваться уравнением
Клапейрона – Менделеева, составив его
для каждого из двух состояний пара.
39.
Обозначим параметры состояния парадо его охлаждения через рп ,V, Tп и будем
считать, что его масса равна mп. Тогда,
уравнению Клапейрона – Менделеева,
pп V = (mп/Мп)RTп
После охлаждения и конденсации,
когда пар в трубке будет насыщающим, его
масса станет равной mнп, а параметры
примут значения pнп ,V и Tнп. Для
насыщающего пара уравнение КлапейронаМенделеева
pнп ·V = (mнп/Мнп) ·RTнп.
40.
При составлении мы не учитывалиобъем, занимаемый каплями, так как он
достаточно мал, и считали давление
насыщающего пара известным (из
таблиц), так как температура его Tнп
дана. Для определения массы росы,
выпавшей на стенках трубки,
составляем вспомогательное уравнение
m = mп ─ mнп ,где m─ искомая масса
росы. Решая полученные уравнения,
находим
m = 9 мг.
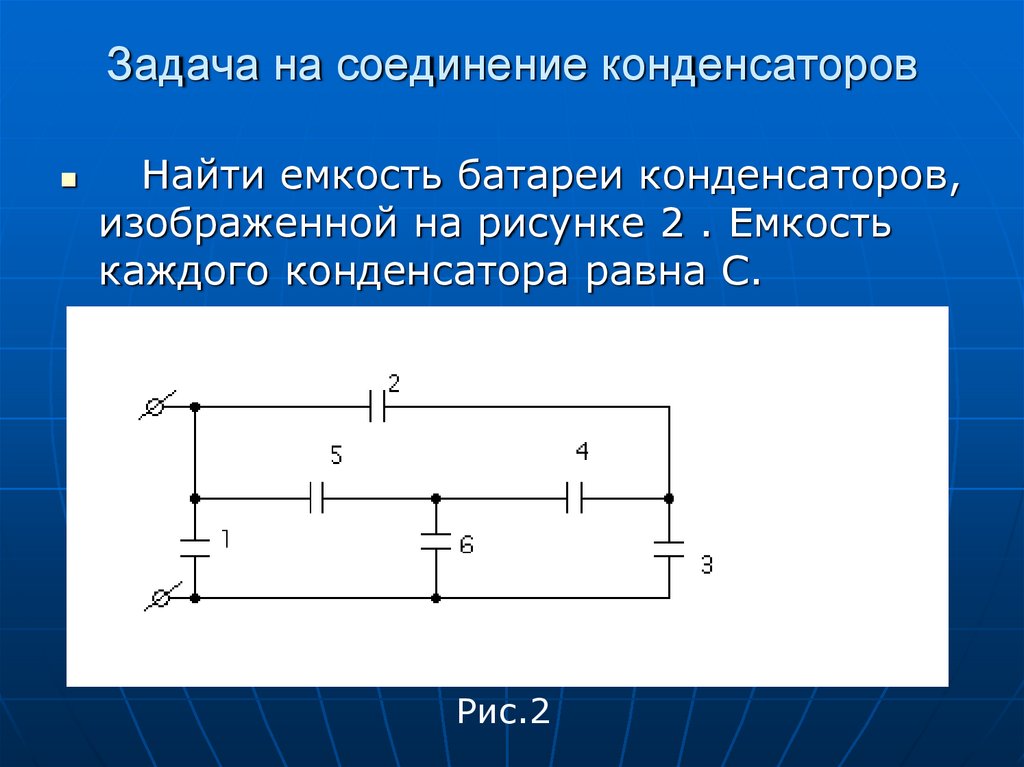
41. Задача на соединение конденсаторов
Найти емкость батареи конденсаторов,изображеннoй на рисунке 2 . Емкость
каждого конденсатора равна С.
Рис.2
42. Решение
Изобразим эквивалентную схему.Поскольку конденсаторы 1,2,5
соединены одноименными обкладками,
следовательно, они соединены
параллельно. Конденсатор 5 и 6
соединены противоположно
заряженными т.е. последовательно.
Аналогично 2 и 3.
43. Рисунок 3
Итак, на рисунке 3 каждый изконденсаторов соединен с источником и
с другими конденсаторами точно также,
как в исходной схеме
Рис.3
44.
Вследствие равенства емкостей всехконденсаторов разность потенциалов
между точками А и В равна нулю.
Поэтому конденсатор С4 не заряжен и
его емкость можно не учитывать. Его
уберем из схемы и получим более
упрощенную эквивалентную схему. В
результате получаем схему из трех
параллельных ветвей, две из которых
содержат по два последовательно
включенных конденсатора (рис.4).
45. Упрощенная эквивалентная схема
Рис.446.
Найдем общую емкость системы:С2,3 = С2 ∙ С3 / (С2 + С3) = С/2;
С5,6 = С/2;
С = С1 + С2,3 + С5,6 = С + С/2 +
С/2 = 2С.
Ответ: 2С
47. Задача по атомной физике
Рассматривая электрон какклассическую частицу,
движущуюся в атоме водорода по
круговой орбите вокруг
неподвижного протона, выразите
скорость v электрона и его
механическую энергию W через
радиус r орбиты.
48. Решение
Сила Кулона F = е2 /4πε0 r2 сообщаетэлектрону центростремительное
ускорение ац = υ2/r.
Из второго закона Ньютона следует:
υ= e /√(4πε0mr)
Отсюда находим энергию
движущегося вокруг ядра электрона:
W = mυ2/2 ─ e2 /4πε0 r = ─ e2 /8πε0 r.
49.
Она отрицательна, как и должнобыть для связанной частицы, которая не
может уйти на бесконечность ( нулевой
уровень потенциальной энергии здесь,
соответствует бесконечно большому
расстоянию между частицами)















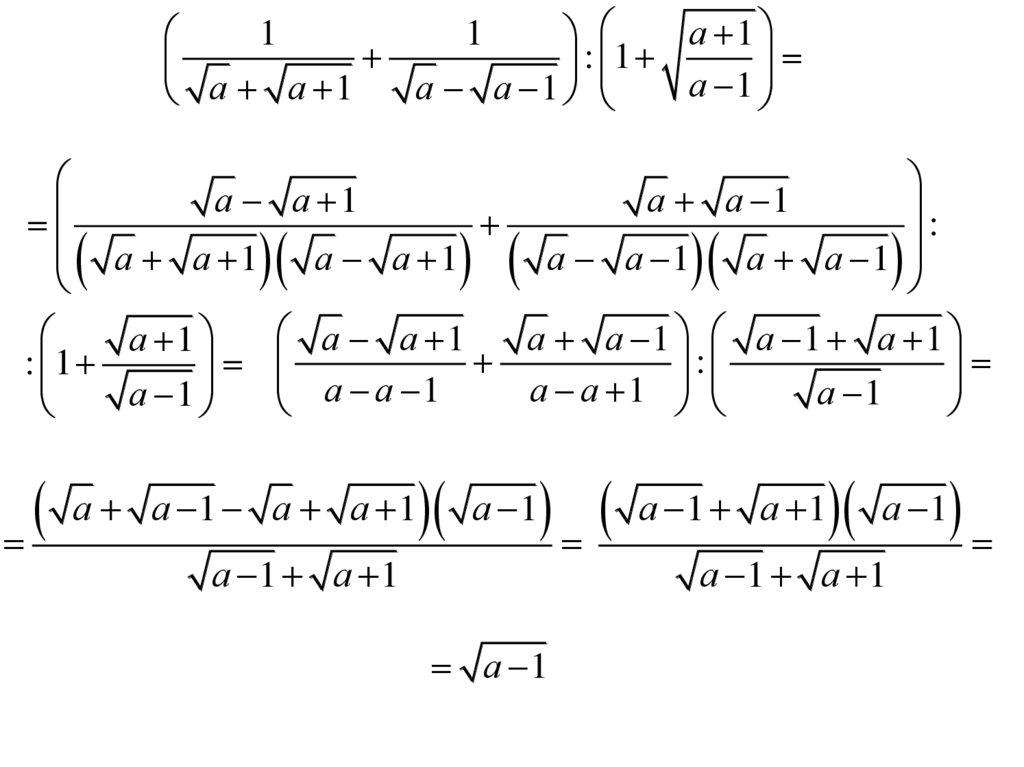




























 mathematics
mathematics








