Простейшие задачи в координатах. Урок геометрии в 9 классе

1. Простейшие задачи в координатах

Урок геометрии в 9 классе
Простейшие задачи в
координатах
Учебник:
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия 7 – 9
классы
Учитель математики:
Мохова В.И.

2. Диктант

Запишите разложение по координатным векторам i и j вектора a 2; -1 .
Выпишите координаты вектора c , если его разложение по координатным
векторам имеет вид c = - i + 2 j .
Найдите координаты вектора в , равного разности векторов m и t , если m
t 0; -4 .
Найдите координаты вектора 3 d , если d
4; -2 .
Дано: a 3; -2 , b 2; -3 . Найдите координаты вектора
Диагонали параллелограмма ABCD
через векторы СВ и СD.
-5;0 ,
m = a - 4 b .
пересекаются в точке О. Выразите вектор СО
Диагонали ромба равны 6 см и 8 см. Найдите его сторону.
Начертите прямоугольную систему координат Oxy и координатные векторы i и j .
Постройте вектор a -3, 1 с началом в точке O .

3. Тема урока

Простейшиеабаааба
задачи в координатах
аааббб
ааббааб
ббаббба

4.

Теоретический вопрос
ответ
Разложение вектора по координатным векторам.
.
Связь координат вектора с его разложением по
координатным векторам
Правила нахождения координат суммы двух
векторов.
Правила нахождения координат разности двух
векторов.
Правило нахождения произведения вектора на
число.
Формула координат вектора через координаты
его начала и конца.
Как найти координаты середины отрезка?
Как вычислить длину вектора по его
координатам?
Как найти расстояние между двумя
точками?
?
?
?

5. Метод координат КООРДИНАТЫ СЕРЕДИНЫ ОТРЕЗКА

у
А(x1;y1)
C(x;y)
В(x2;y2)
j
О
А(x1;y1)
i
х
x1 x2
x
2
В(x2;y2)
1
OC OA OB
2
OC x; y
OA x1; y1
OB x2 ; y2
y1 y2
y
2
• КАЖДАЯ КООРДИНАТА СЕРЕДИНЫ ОТРЕЗКА РАВНА
ПОЛУСУММЕ СООТВЕТСТВУЮЩИХ КООРДИНАТ ЕГО КОНЦОВ

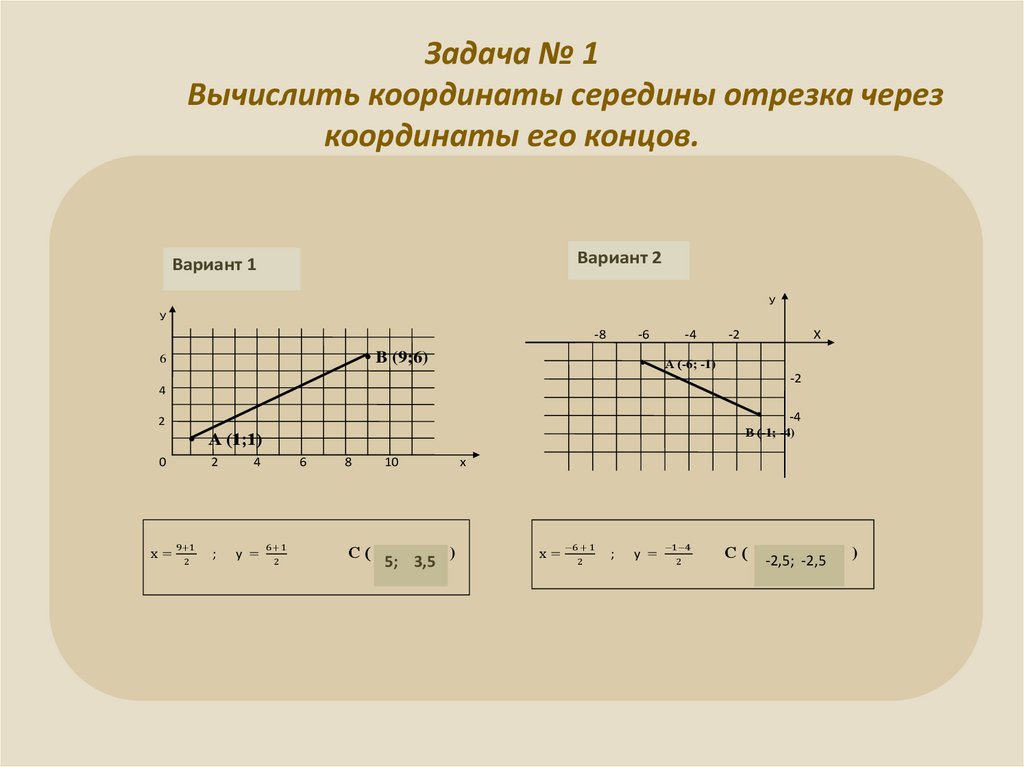
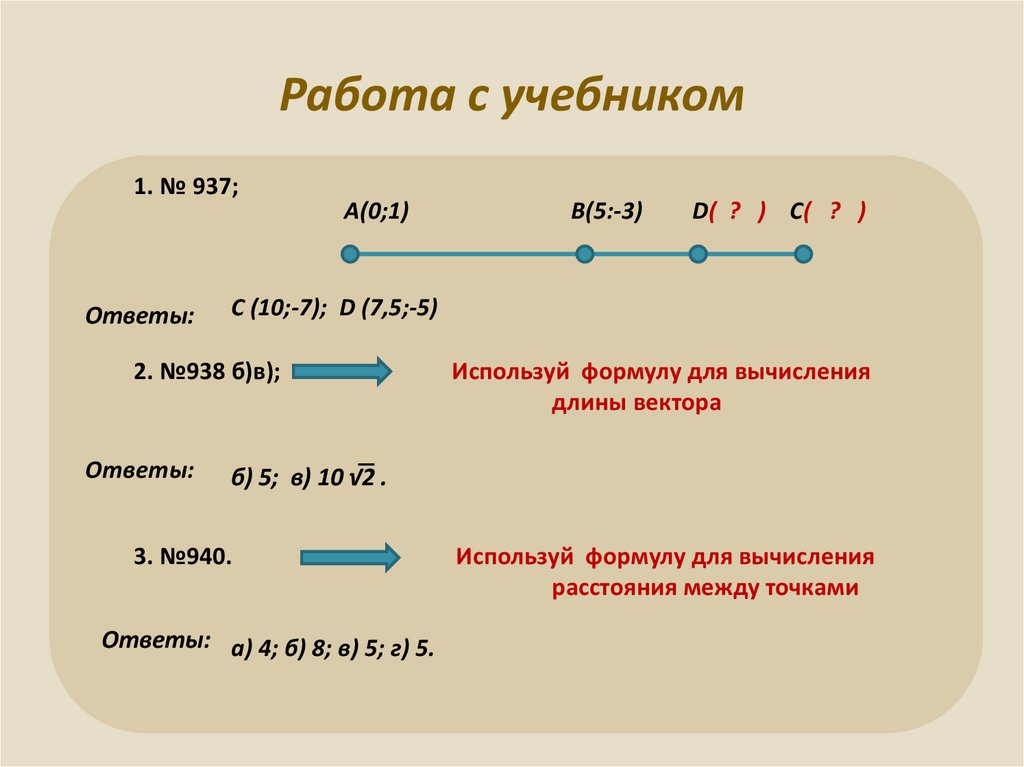
6. Задача № 1 Вычислить координаты середины отрезка через координаты его концов.

Вариант 2
Вариант 1
У
У
-8
• B (9;6)
6
-6
-4
А (-6; -1)
-2
Х
-2
4
2
• А (1;1)
0
х=
9+1
2
2
4
;
у =
-4
В (-1; -4)
6
6+ 1
2
8
С(
10
5; 3,5
х
)
х=
−6 + 1
2
;
у =
−1−4
2
С(
-2,5; -2,5
)

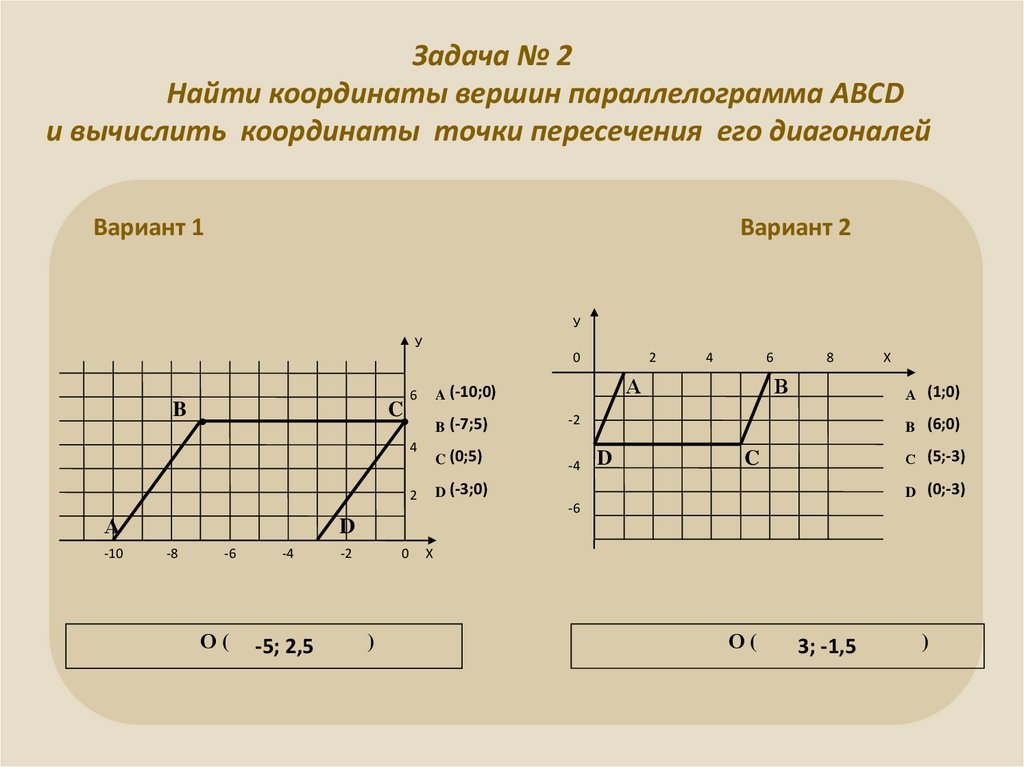
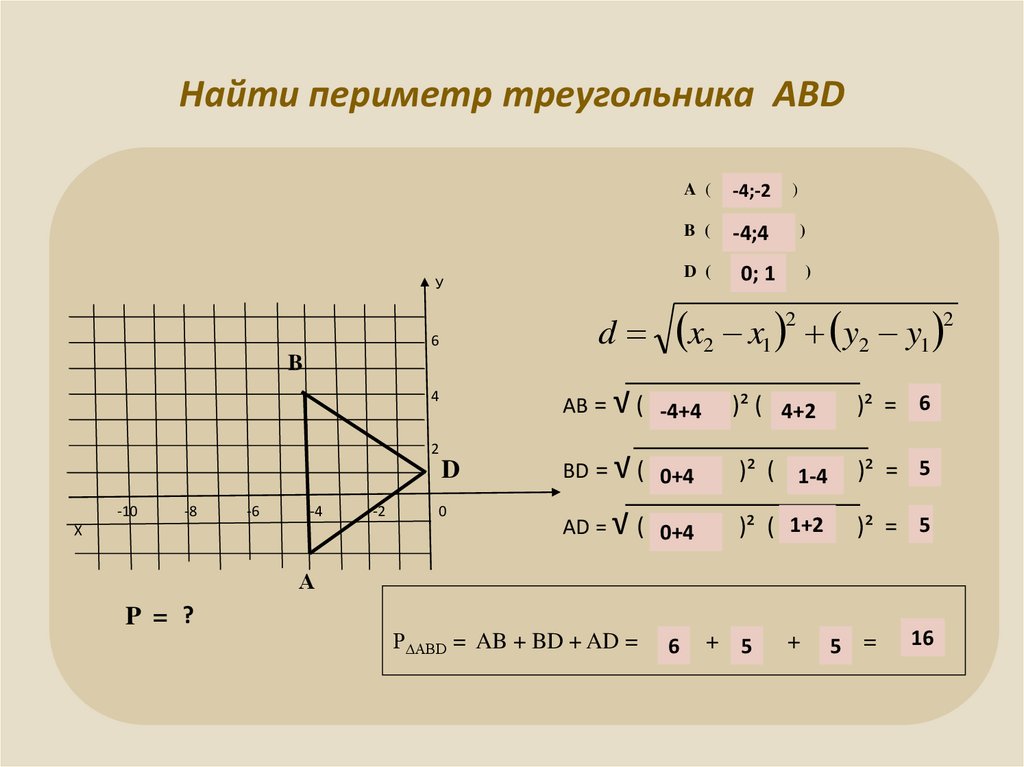
7. Задача № 2 Найти координаты вершин параллелограмма АВСD и вычислить координаты точки пересечения его диагоналей

Вариант 1
Вариант 2
У
У
0
B
C
4
\
-10
6
B (-7;5)
-2
C (0;5)
-4
8
В
Х
А (1;0)
B (6;0)
D
С (5;-3)
C
D (-3;0)
2
А
4
А
A (-10;0)
6
2
D (0;-3)
-6
D
-8
-6
О(
-4
-5; 2,5
-2
0
)
Х
О(
3; -1,5
)

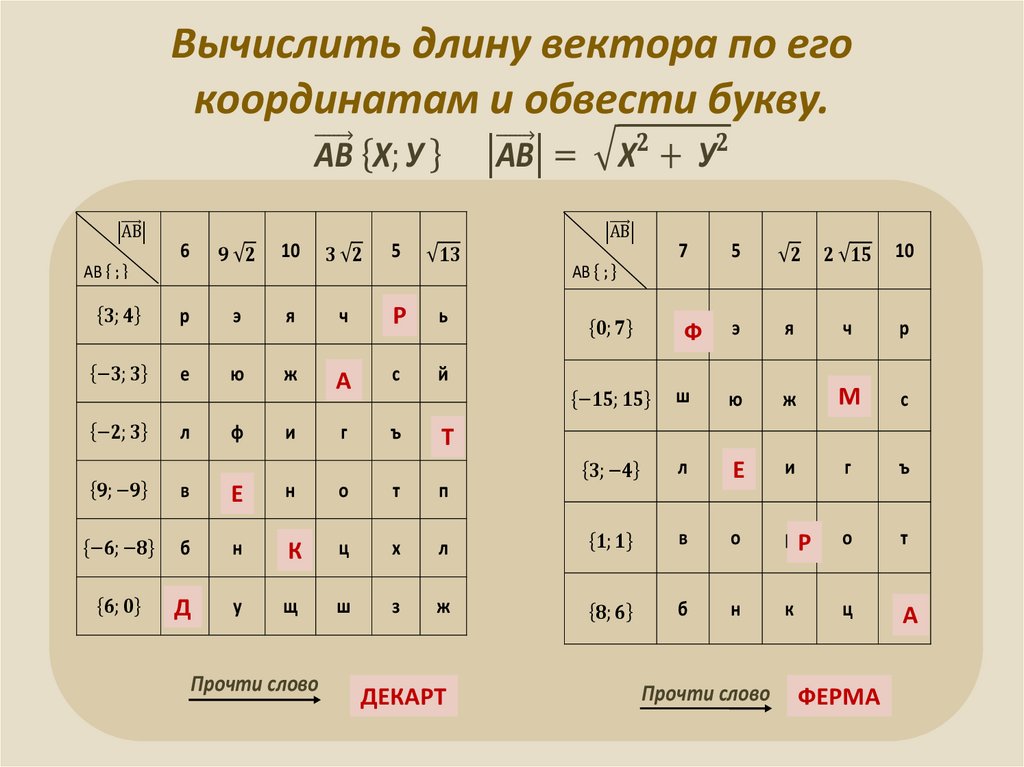
8. Метод координат ВЫЧИСЛЕНИЕ ДЛИНЫ ВЕКТОРА ПО ЕГО КООРДИНАТАМ

OA a
у
А2
О
OA a x; y
AA1 OA2 y
А(x;y)
OA1 x
a
А1
х
OA OA AA1 x 2 y 2
2
1
2
a OA OA
ДЛИНА ВЕКТОРА
a x; y
ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ
a x y
2
2

9. Вычислить длину вектора по его координатам и обвести букву.

Х