Similar presentations:
Касательная к окружности
1. КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
Учитель математики ГБОУ гимназии №1504Железнова Я.А.
2. Давайте вспомним:
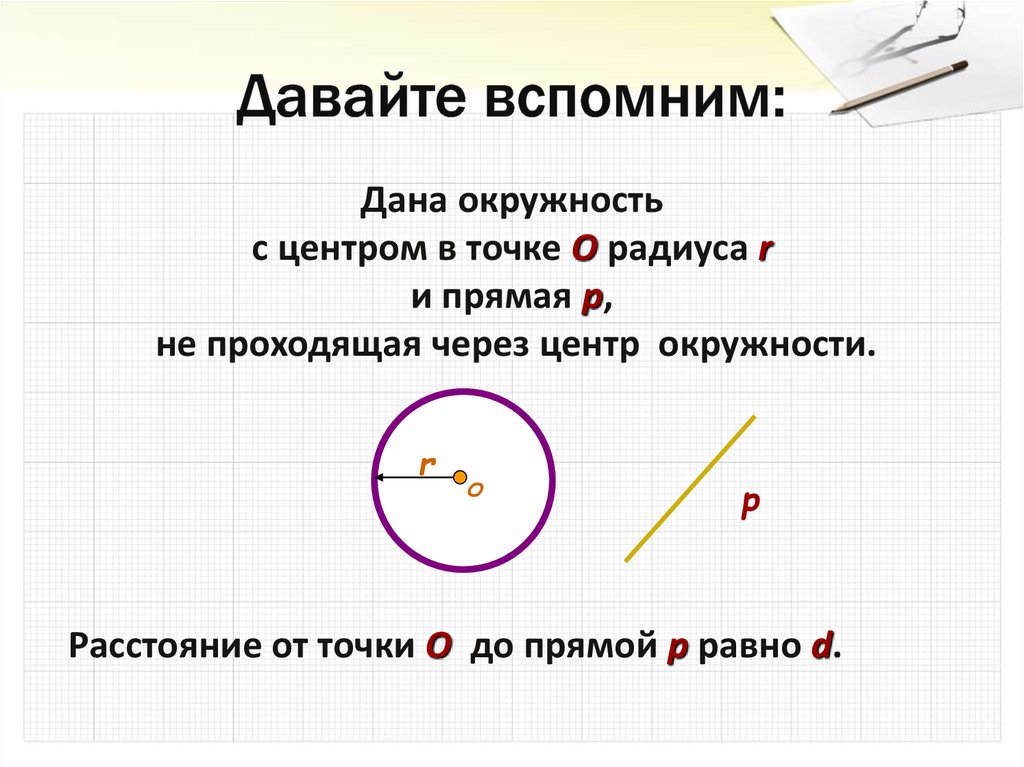
Дана окружностьс центром в точке О радиуса r
и прямая p,
не проходящая через центр окружности.
r
о
p
Расстояние от точки О до прямой p равно d.
3. Среди следующих утверждений укажите истинные
Окружность и прямая имеют две общие точки,если:
а) расстояние от центра окружности до прямой не
превосходит радиуса окружности;
б) расстояние от центра окружности до прямой
меньше радиуса окружности;
в) расстояние от окружности до прямой меньше
радиуса.
4. Закончите фразы, чтобы получилось верное высказывание
Окружность и прямая не имеют общихточек, если...
расстояние от центра окружности до
прямой больше радиуса окружности
Окружность и прямая имеют одну
общую точку, если…
расстояние от центра окружности до
прямой равно радиусу окружности
5. Установите истинность или ложность следующих утверждений:
а) Прямая а является секущей по отношению кокружности, если она имеет с окружностью
общие точки.
б) Прямая а является секущей по отношению к
окружности, если она пересекает окружность в
двух точках.
в) Прямая а является секущей по отношению к
окружности, если расстояние от центра
окружности до данной прямой не больше
радиуса.
6. Касательная
Прямая, имеющая сокружностью
только одну общую точку,
называется
КАСАТЕЛЬНОЙ к
окружности.
Прямая P касательная
Точка А - точка
касания прямой и
окружности
7. Свойство касательной
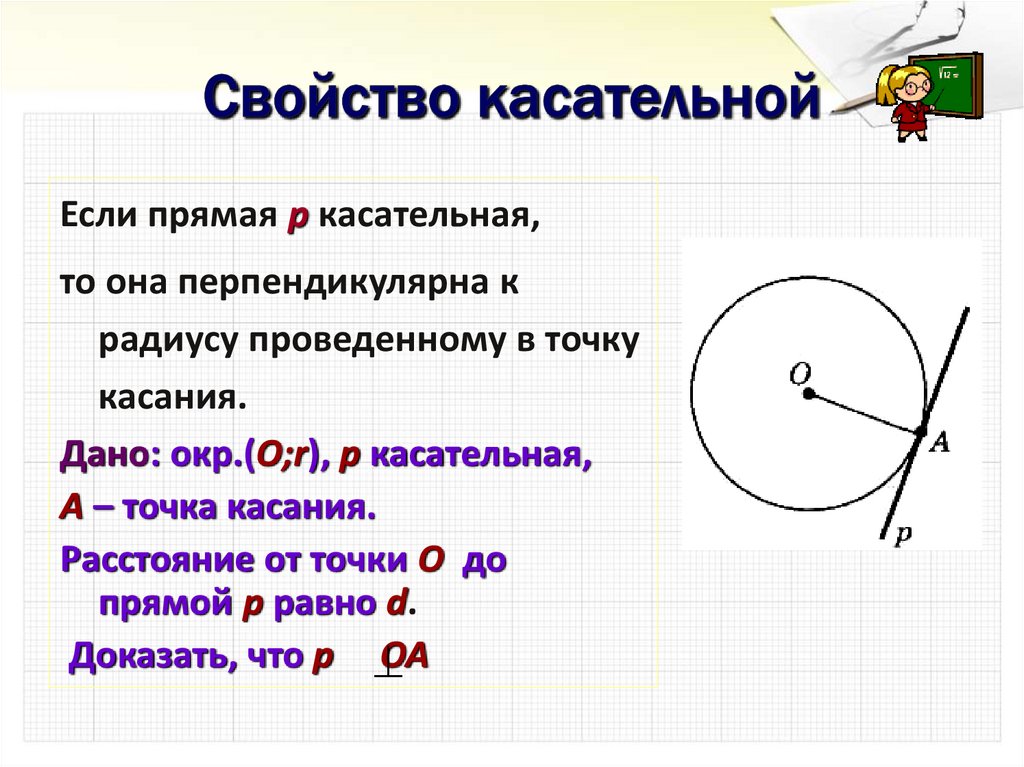
Если прямая р касательная,то она перпендикулярна к
радиусу проведенному в точку
касания.
Дано: окр.(О;r), р касательная,
А – точка касания.
Расстояние от точки О до
прямой p равно d.
Доказать, что р
ОА
8.
ДоказательствоДопустим, что р ОА.
Сравним
расстоян
ие от
центра
окружнос
ти до
прямой р
с
радиусом
окружнос
ти.
Тогда радиус ОА –наклонная к
прямой р.
Т.к. перпендикуляр
проведенный из т.О меньше
наклонной ОА, то d<r
Значит прямая и окружность
имеют две общие точки
Это противоречит условию: р –
Каково
касательная.
взаимное
Значит р
ОА
располож
ение
прямой р
9. ОТРЕЗКИ КАСАТЕЛЬНЫХ
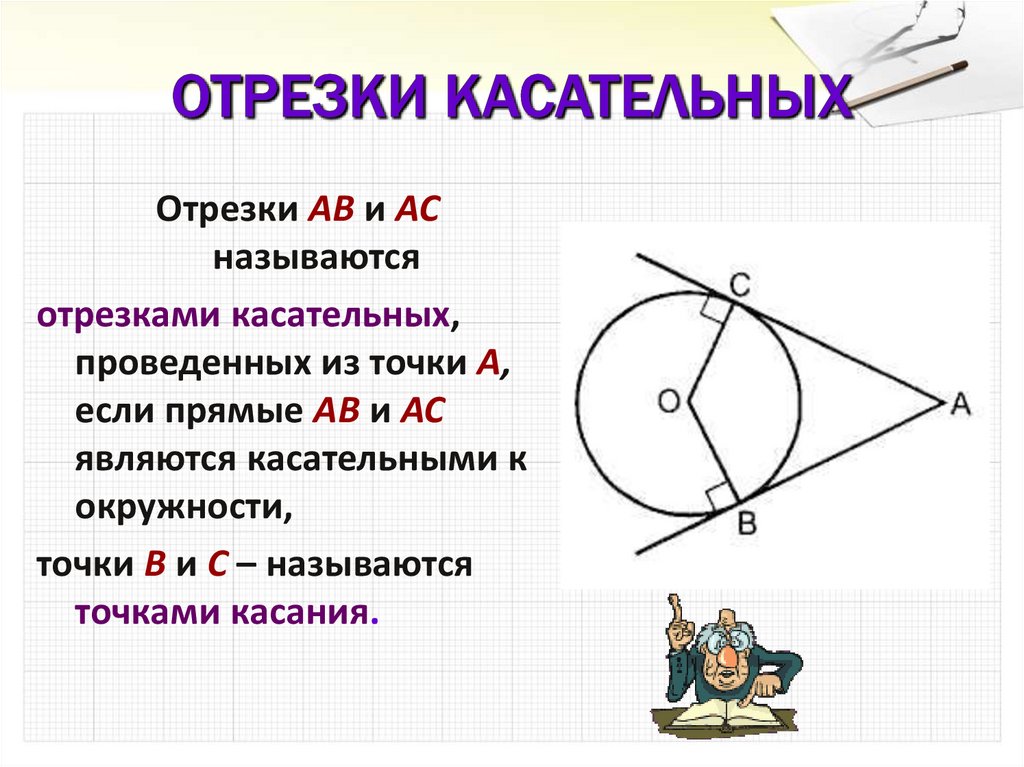
Отрезки АВ и АСназываются
отрезками касательных,
проведенных из точки А,
если прямые АВ и АС
являются касательными к
окружности,
точки В и С – называются
точками касания.
10. Свойство отрезков касательных
Отрезки касательных к окружности,проведенных из одной точки, равны и
составляют равные углы с прямой,
проходящей через эту точку и центр
окружности.
11. Дано:
aА
ОКР (О; R)
АВ и АС отрезки
касательных
т. В и С –точки касания
А, О а
Доказать, что
АВ = АС и
3 4
3 4
В
С
О
12. Доказательство
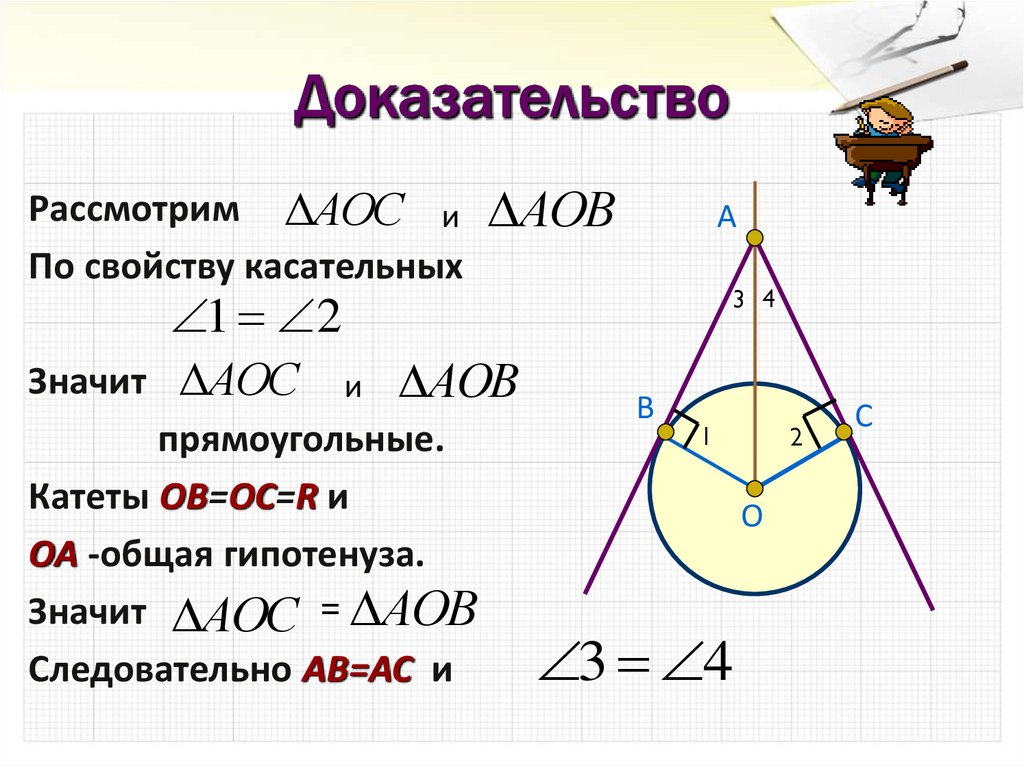
Рассмотрим АОС иПо свойству касательных
АОВ
1 2
Значит АОС и АОВ
прямоугольные.
Катеты ОВ=ОС=R и
ОА -общая гипотенуза.
Значит АОС = АОВ
Следовательно АВ=АС и
А
3 4
В
1
2
О
3 4
С
13. Сформулируйте обратное утверждение
Если прямая проходит через конецрадиуса, лежащий на окружности, и
перпендикулярна к этому радиусу, то она
является касательной.
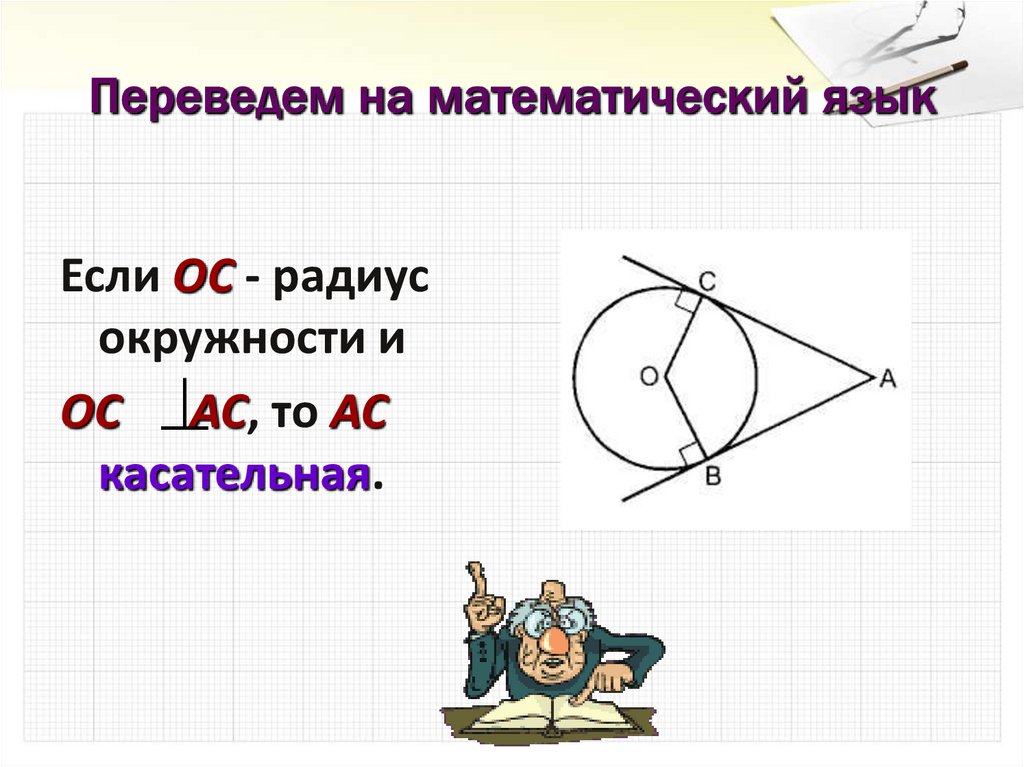
14. Переведем на математический язык
Если ОС - радиусокружности и
ОС АС, то АС
касательная.
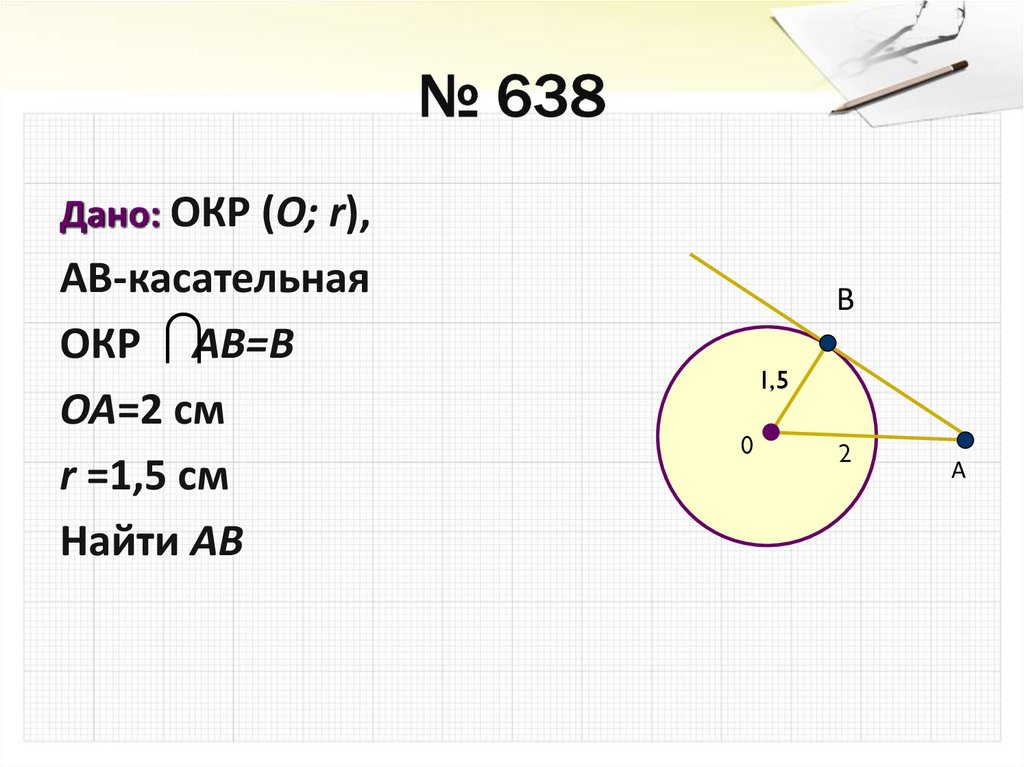
15. № 638
Дано: ОКР (О; r),AB-касательная
ОКР AB=B
ОА=2 см
r =1,5 см
Найти АВ
В
1,5
0
2
А
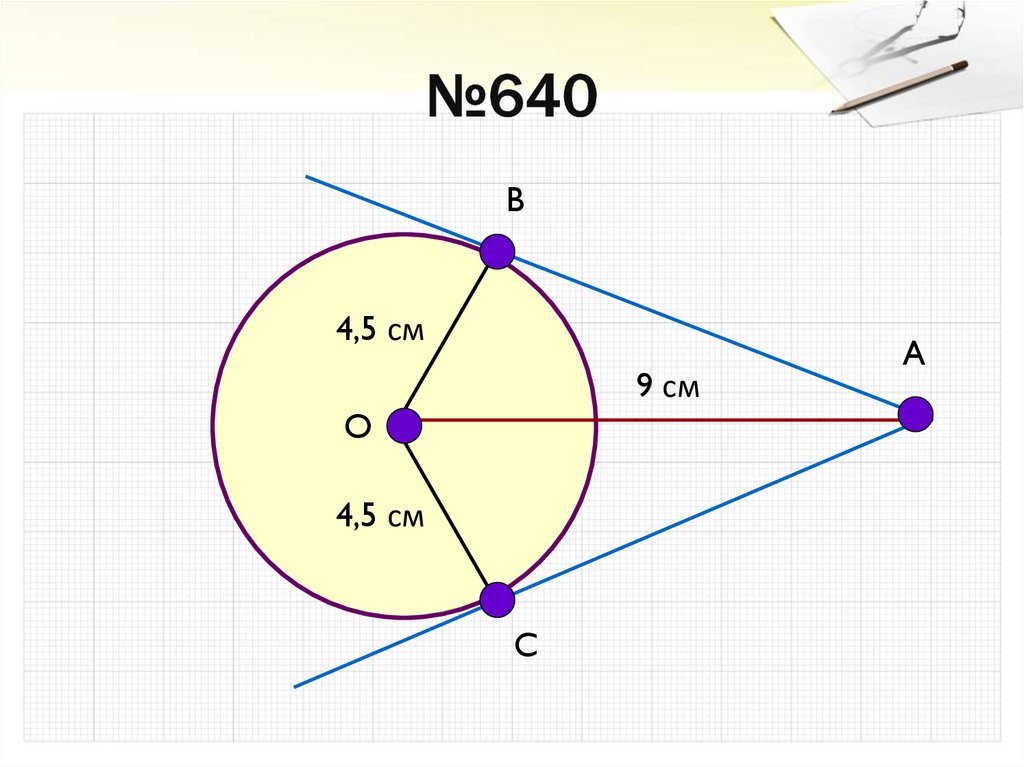
16. №640
B4,5 см
9 см
O
4,5 см
C
A
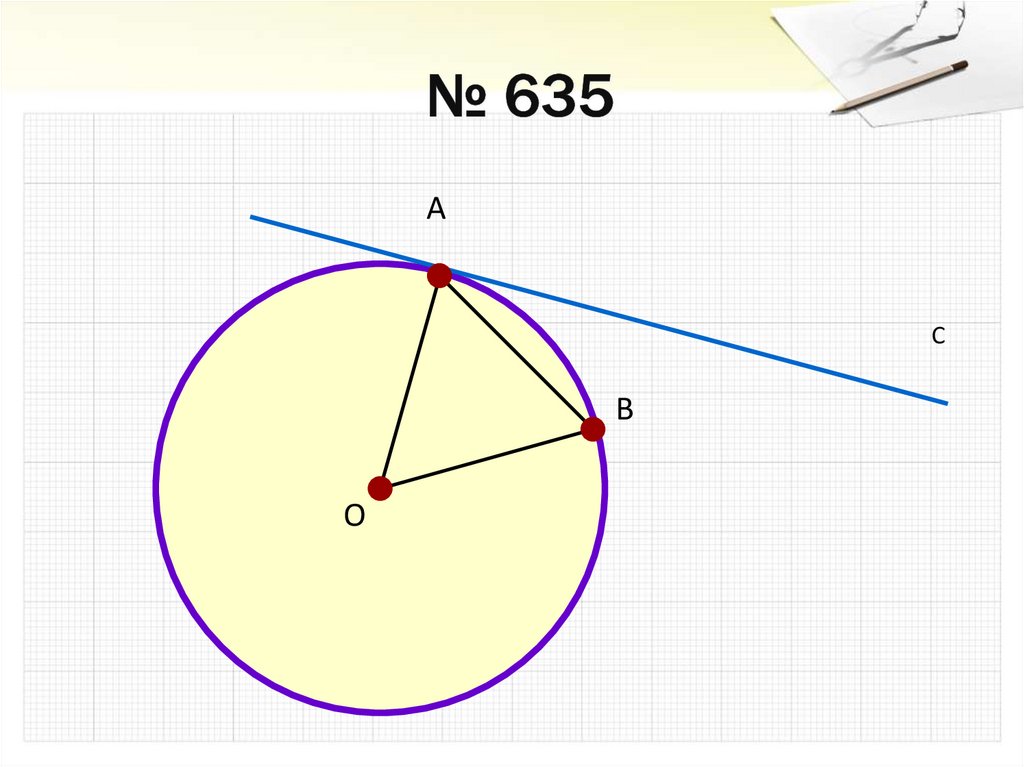
17. № 635
АС
В
О
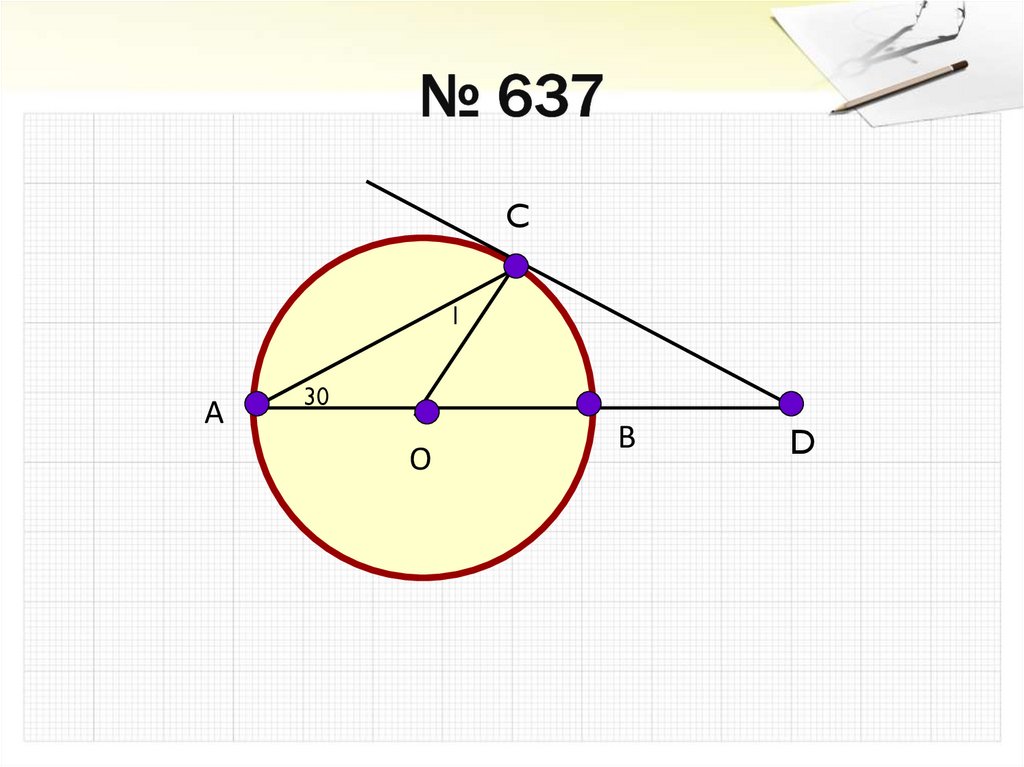
18. № 637
C1
А
30
О
В
D
19. Подведение итогов
20. Домашнее задание
П. 69 определение касательной, свойствокасательной, свойство отрезков
касательной, признак касательной
№ 636,638,639











 mathematics
mathematics








