Построение сечений многогранников

1.

Тема:
Построение сечений многогранников
Цель урока:
Рассмотреть способы
построения сечений многогранников

2. При построении сечения фигуры плоскостью необходимо помнить:

Через любые две точки плоскости проходит
прямая и притом только одна.
Если две параллельные плоскости пересечены
третьей, то линии их пересечения параллельны

3.

Задача 1.
АВСDA1B1C1D1 – четырехугольная призма. Точка К принадлежит ребру В1С1.
Постройте сечение этой призмы плоскостью, проходящей через точки В, D и К.
Р
K
C1
B1
М
А1
1) пл. (АВСD): ВD прямая
D1
2) пл.(ВB1C1С): ВК ∩ C1С = Р
3) пл. (D D1 C1С): DР ∩ D1C1 = М
4)
В
А
С
D
пл. (А1В2С1D1): прямая МК

4.

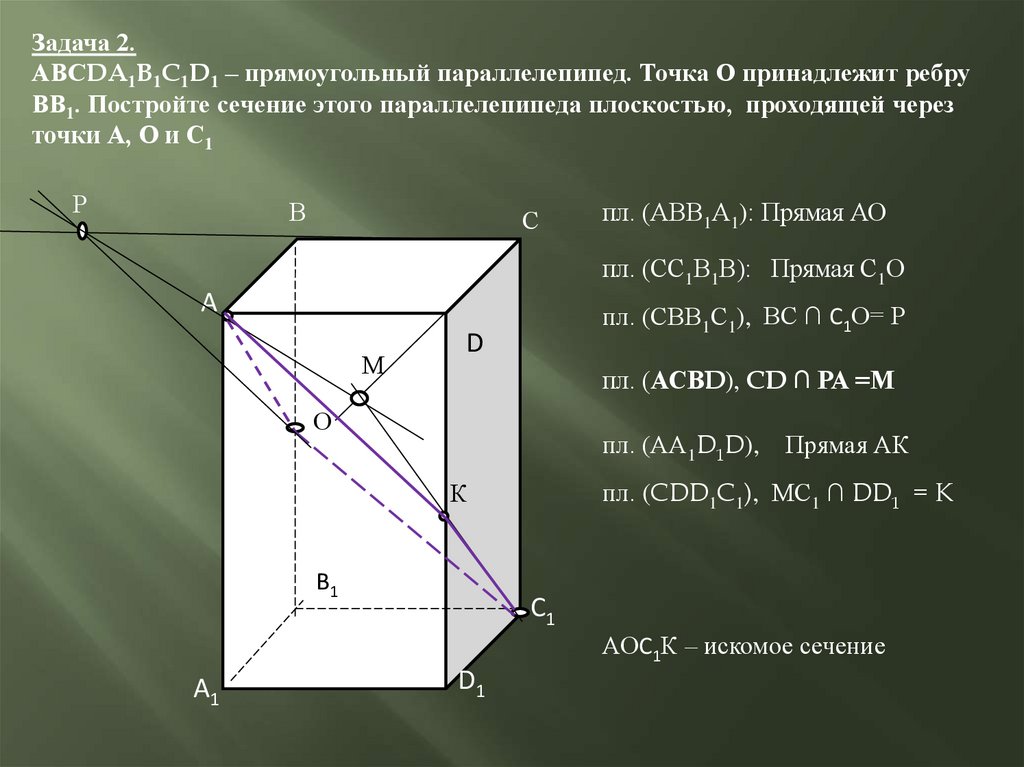
Задача 2.
АВСDA1B1C1D1 – прямоугольный параллелепипед. Точка О принадлежит ребру
ВВ1. Постройте сечение этого параллелепипеда плоскостью, проходящей через
точки А, О и С1
Р
В
С
пл. (АВВ1А1): Прямая АО
пл. (СС1В1В): Прямая С1О
А
М
пл. (СВВ1С1), ВС ∩ С1О= Р
D
пл. (АСВD), CD ∩ РА =М
О
пл. (АА1D1D),
пл. (CDD1C1), МС1 ∩ DD1 = K
К
В1
Прямая АК
С1
АОС1К – искомое сечение
А1
D1

5.

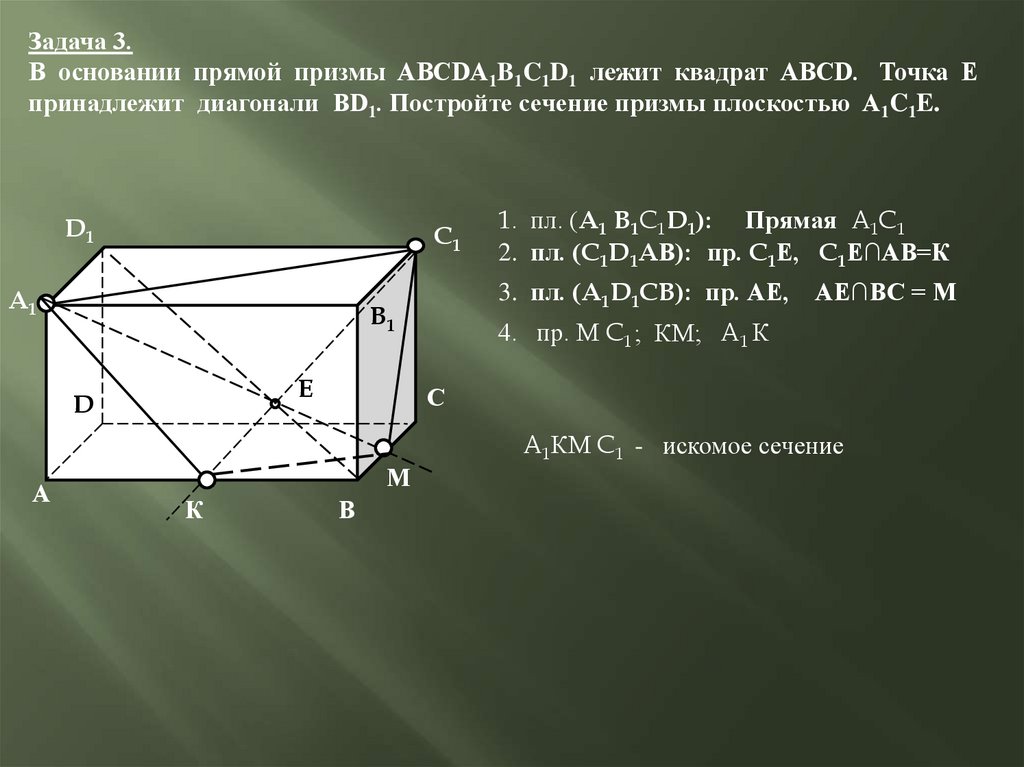
Задача 3.
В основании прямой призмы ABCDA1B1C1D1 лежит квадрат ABCD. Точка E
принадлежит диагонали BD1. Постройте сечение призмы плоскостью A1C1E.
D1
C1
A1
А
3. пл. (A1D1CB): пр. АЕ,
B1
E
D
АЕ∩ВС = М
4. пр. М C1 ; КМ; A1 К
С
М
К
1. пл. (A1 B1C1D1): Прямая A1C1
2. пл. (C1D1AВ): пр. C1Е, C1Е∩АВ=К
В
A1КМ C1 - искомое сечение