Similar presentations:
Методы перевода чисел из ПСС в СОК и обратно
1. Занятие № 3 (Лекции 5, 6). Методы перевода чисел из ПСС в СОК и обратно
Методы перевода чисел из ПСС в СОКПервый метод. Метод основан на использовании формулы
A
ai A mi
mi
для i 1, n .
В этом случае из исходного числа A для набора оснований
СОК mi получаем совокупность остатков ai , i 1, n . Число в
СОК представится в виде A ( a1 , a2 ,..., an ) .
1
2.
Второй метод. Метод осуществляется с помощью набораконстант, являющихся эквивалентами оснований P ПСС, которые
представляются в СОК.
Пусть задано число A в ПСС
r
A ( ar P r ar 1 P r 1 ... a1 P a0 ) ai Pi ,
i 0
ai 1, P 1 ,
пусть основание ПСС представляется в СОК по основаниям
m1 , m2 , ..., mn
P ( i ) 1( i ) , 2( i ) , ..., n( i ) , i 1, r .
Величины ai 1( i ) , 2( i ) , ..., n( i ) представлены также в СОК.
2
3.
Число A (Q1 , Q2 ,..., Qn ) (1) представляется в СОК, гдеQ j (ji ) (j i )
r
(2),
j 1, n .
i 0
Для образования числа A в СОК требуется r констант,
являющихся степенями оснований P ПСС и ( P 1) констант,
соответствующих возможным значениям коэффициентов ai , т.е. в
общем случае необходимо всего ( r P 1) констант.
3
4.
Пример реализации второго метода преобразования чисел изПСС в СОК.
Перевести число A 102 из десятичной ПСС в СОК с
основаниями m1 3 , m2 5 , m3 7 .
Константы для значений r и P представляются в следующем
виде
P 0 1 (1, 1, 1) , P1 10 (1, 0, 3) , P 2 100 (1, 0, 2) ;
a0 2 (2, 2, 2) , a1 0 (0, 0, 0) , a2 1 (1, 1, 1) .
Тогда в соответствии с выражениями (1, 2 слайд 3) имеем, что
A (2 1 0 1 1 1),(2 1 0 0 1 0),(2 1 0 3 1 2) 0, 2, 4
m1 3
m2 5
m1 7
Проверка: A 102 (0, 2, 4) .
4
5. Метод перевода чисел из СОК в ПСС
Пусть задана СОК основании m1 , m2 , ..., mn . Зададим n чиселB1 , B2 ,..., Bn в СОК, где B j b1( j ) , b2( j ) , ..., bn( j ) , j 1, n , которые
называются базисами СОК.
Это одни из основных констант СОК. Они рассчитываются
заранее по основаниям СОК и хранятся в ПЗУ в СОК и в ПСС.
Пусть необходимо перевести число A ( a1 , a2 ,..., an ) из СОК в
ПСС. Задача перевода заключается в том, что необходимо
определить числа 1 , 2 ,..., n , такие, что
1 B1 2 B2 ... n Bn A .
(1)
5
6.
Перепишем выражение (1) в СОК1 [b1(1) , b2(1) ,..., bn(1) ] 2 [b1(2) , b2(2) ,..., bn(2) ] ...
... n [b1( n ) , b2( n ) ,..., bn( n ) ] [a1, a2 , ..., an ] .
Для определения величины i , i 1, n , необходимо решить
систему линейных алгебраических уравнений
1 b1(1) 2 b1(2) ... n b1( n ) a1 ,
(1)
(2)
(n)
b
b
...
b
a2 ,
1 2
2
2
n
2
b(1) b(2) ... b( n ) a .
1 n
2
n
n
n
n
6
7.
Система уравнений будет иметь целые решения, еслиопределитель матрицы будет равен 1, т.е.
b1(1) b1(2) ... b1( n )
b2(1) b2(2) ... b2( n )
1 .
bn(1) bn(2) ... bn( n )
7
8.
Имеется большой выбор величин b1 , b2 ,..., bn , поскольку любаявозможная система величин b(ji ) приемлема в качестве базиса. В
частности, в качестве базисов СОК предполагаются следующие
величины B1 (1, 0, 0, ..., 0) , B2 (0, 1, 0, ..., 0) … Bn (0, 0, 0, ..., 0, 1) .
Их называют ортогональные базисы. В этом случае для
ортогональных базисов получим
1 a1 ,
a ,
2
2
n an .
Откуда, A ( a1 B1 a2 B2
1 0 0 ... 0
0 1 0 ... 0
1
0 0 0 ... 1
an Bn ) mod M ,
n
M mi .
i 1
8
9.
ПримерЗадана СОК m1 3 , m2 5 и m3 7 . M 3 5 7 105 .
Перевести число A (2, 3, 5) в десятичную ПСС. Ортогональные
базисы
имеют
вид
B1 (1, 0, 0) 70 ,
B2 (0, 1, 0) 21,
B3 (0, 0, 1) 15 .
A (2, 3, 5) 2 B1 3 B2 5 B3
2 70 3 21 5 15 278 68(mod105) .
Для того чтобы реализовать процедуру перевода чисел из СОК
в ПСС необходимо определить Bi ( i 1, n ).
9
10.
По определению ортогональных базисов они могут бытьпредставленными в виде
mi M
, i 1, n , где mi – целое
Bi (0, 0, ..., 0, 1, 0, ..., 0, 0) , Bi
mi
положительное число (вес ортогонального базиса).
Причём mi выбирается таким образом, чтобы имело место
сравнение
mi M
mi M
li mi 1.
1(mod mi ) или
mi
mi
(2)
10
11.
Вариант вычисления веса mi ортогонального базиса.M
Введём обозначение M i
. Разделим M i на mi . Так как значение
mi
M i составлено из множителей взаимно простых с mi , оно нацело не
делится, т.е. будет определенный остаток i . Тогда в соответствии
с формулой (2) значение mi округлится как результат решения
сравнения
mi i 1(mod mi ) .
Ввиду малости оснований mi , i СОК, значение
выбирается по числу i табличным образом (или перебором).
mi
11
12.
Общий алгоритм определения Bi .n
1. По значениям mi , определяем M mi .
i 1
M
2. Определяем значения M i
.
mi
3. Вычисляем значения i M i (mod mi ) .
4. По значениям i в выражении mi i 1(mod mi ) подбираем
(перебором) значение mi .
5. Bi mi M i .
Для контроля вычислений ортогональных базисов Bi можно
воспользоваться соотношением
n
B
i 1
i
1(mod M ) .
12
13. Метод определения ортогональных базисов
В соответствии с общим алгоритмом для СОК заданнойоснованиями m1 3 , m2 5 , m3 7 и m4 17 ( n 4 ), определим
ортогональные базисы
(i 1, n ) .
Bi
правильности полученного результата.
1. Определение значения модуля
n
4
i 1
i 1
Провести
проверку
M mi mi 3 5 7 17 1785 .
2. Определение частных значений модулей M i
M i M / mi :
M1 M / m1 5 7 17 595 ;
M 2 M / m2 3 7 17 357 ;
M 3 M / m3 3 5 17 255 ;
M 4 M / m4 3 5 7 105 .
(i 1, n )
13
14.
3. Определим значения i M i (mod mi ) для i 1, 4 :1 M1 (mod m1 ) 595(mod 3) 1;
2 M 2 (mod m2 ) 357(mod 5) 2 ;
3 M 3 (mod m3 ) 255(mod 7) 3 ;
4 M 4 (mod m4 ) 105(mod 17) 3 .
14
15.
4. Исходя из условия mi i 1(mod mi ) определим веса mi( i 1, 4 ) ортогональных базисов Bi , где mi 1, mi 1.
m1 1 1(mod m1 ) ; 1 1 ; m1 1, 2 ; m1 3 .
m1 1 ; 1 1 ; m1 1 ( m1 1) mod m1 (1 1) mod 3 1(mod 3) 1 ;
m1 2 ; 1 1 ; m1 1 ( m1 1) mod m1 (2 1) mod 3 2(mod 3) 2 .
m1 1
15
16.
m2 2 1(mod m2 ) ; 2 2 ; m2 1, 4 ; m2 5 .m2 1; 2 1; m2 2 (mod m2 ) (1 2) mod 5 2(mod 5) 2 ;
m2 2 ; 2 1; m2 2 (mod m2 ) (2 2) mod 5 4(mod 5) 4 ;
m2 3 ; 2 2 ; m2 2 (mod m2 ) (3 2) mod 5 6(mod 5) 1;
m2 4 ; 2 2 ; m2 2 (mod m2 ) (4 2) mod 5 8(mod 5) 3 .
m2 3
16
17.
m3 3 1(mod m3 ) ; 3 3 ; m3 1, 6 ; m3 7 .m3 1 ; 3 1 ; m3 3 (mod m3 ) (1 3) mod 7 3(mod 7) 3 ;
m3 2 ; 3 1 ; m3 3 (mod m3 ) (2 3) mod 7 6(mod 7) 6 ;
m3 3 ; 3 3 ; m3 3 (mod m3 ) (3 3) mod 7 9(mod 7) 2 ;
m3 4 ; 3 3 ; m3 3 (mod m3 ) (4 3) mod 7 12(mod 7) 5 ;
m3 5 ; 3 3 ; m3 3 (mod m3 ) (5 3) mod 7 15(mod 7) 1;
m3 6 ; 3 3 ; m3 3 (mod m3 ) (6 3) mod 7 18(mod 7) 4 .
m3 5
17
18.
m4 4 1(mod m4 ) ; 4 3 ; m4 1, 16 ; m4 17 .m4 1; 4 3 ; (1 3) mod17 3(mod17) 3 ;
m4 2 ; 4 3 ; (2 3) mod17 6(mod17) 6 ;
m4 3 ; 4 3 ; (3 3) mod17 9(mod17) 9 ;
m4 4 ; 4 3 ; (4 3) mod17 12(mod17) 12 ;
m4 5 ; 4 3 ; (5 3) mod17 15(mod17) 15 ;
m4 6 ; 4 3 ; (6 3) mod17 18(mod17) 1 ;
m4 7 ; 4 3 ; (7 3) mod17 21(mod17) 4 ;
m4 8 ; 4 3 ; (8 3) mod17 24(mod17) 17 ;
18
19.
m4 9 ; 4 3 ; (9 3) mod17 27(mod17) 10 ;m4 10 ; 4 3 ; (10 3) mod17 30(mod17) 13 ;
m4 11; 4 3 ; (11 3) mod17 33(mod17) 16 ;
m4 12 ; 4 3 ; (12 3) mod17 36(mod17) 2 ;
m4 13 ; 4 3 ; (13 3) mod17 39(mod17) 5 ;
m4 14 ; 4 3 ; (14 3) mod17 42(mod17) 8 ;
m4 15 ; 4 3 ; (15 3) mod17 45(mod17) 11 ;
m4 16 ; 4 3 ; (16 3) mod17 48(mod17) 14 .
m4 6
19
20.
5. Определяем значения ортогональных базисов Bi mi M i(i 1, n )
B1 m1 M 1 1 595 595 ;
B2 m2 M 2 3 357 1071;
B3 m3 M 3 5 255 1275 ;
B4 m4 M 4 6 105 630 .
Проверка:
( B1 B2 B3 B4 ) mod M (595 1071 1275 630) mod1785
3571mod 1785 1
20
21.
Пример.Перевести число AСОК (2, 3, 4, 1) из СОК, заданной
основаниями m1 3 , m2 4 , m3 5 и m4 7 в десятичную ПСС.
I этап. Необходимо определить значения ортогональных
базисов Bi (i 1, n ) .
4
1. M mi 3 4 5 7 420 .
i 1
2. Определим M i M / mi
M 1 M / m1 420 / 3 4 5 7 140 ;
M 2 M / m2 420 / 4 3 5 7 105 ;
M 3 M / m3 420 / 5 3 4 7 84 ;
M 4 M / m4 420 / 7 3 4 5 60 .
21
22.
3. Определим значения i M i (mod mi )1 M 1 (mod m1 ) 140(mod 3) 2 ;
2 M 2 (mod m2 ) 105(mod 4) 1 ;
3 M 3 (mod m3 ) 84(mod 5) 4 ;
4 M 4 (mod m4 ) 60(mod 4) 4 .
22
23.
4.Исходя
из
условия
mi i 1
определим
веса
mi
ортогональных базисов Bi ( i 1, 4 ).
m1 1 ; 1 2 ; ( m1 1 ) mod m1 (1 2) mod 3 2(mod 3) 2 ;
m1 2 ; 1 2 ; ( m1 1 ) mod m1 (2 2) mod 3 4(mod 3) 1 .
m1 2
23
24.
m2 1; 2 1 ; ( m2 2 ) mod m2 (1 1) mod 4 1(mod 4) 1 ;m2 2 ; 2 1; ( m2 2 ) mod m2 (2 1) mod 4 2(mod 4) 2 ;
m2 3 ; 2 1 ; ( m2 2 ) mod m2 (3 1) mod 4 3(mod 4) 3 .
m2 1
24
25.
m3 1 ; 3 4 ; ( m3 3 ) mod m3 (1 4) mod 5 4(mod 5) 4 ;m3 2 ; 3 4 ; ( m3 3 ) mod m3 (2 4) mod 5 8(mod 5) 3 ;
m3 3 ; 3 4 ; ( m3 3 ) mod m3 (3 4) mod 5 12(mod 5) 2 ;
m3 4 ; 3 4 ; ( m3 3 ) mod m3 (4 4) mod 5 16(mod 5) 1 .
m3 4
25
26.
m4 1; 4 4 ; ( m4 4 ) mod m4 (1 4) mod 7 4(mod 7) 4 ;m4 2 ; 4 4 ; ( m4 4 ) mod m4 (2 4) mod 7 8(mod 7) 1 ;
m4 3 ; 4 4 ; ( m4 4 ) mod m4 (3 4) mod 7 12(mod 7) 5 ;
m4 4 ; 4 4 ; ( m4 4 ) mod m4 (4 4) mod 7 16(mod 7) 2 ;
m4 5 ; 4 4 ; ( m4 4 ) mod m4 (5 4) mod 7 20(mod 7) 6 ;
m4 6 ; 4 4 ; ( m4 4 ) mod m4 (6 4) mod 7 24(mod 7) 3 .
m4 2
26
27.
5. Определяем ортогональные базисы Bi mi M i (i 1, n )B1 m1 M 1 2 140 280 ;
B2 m2 M 2 1 105 105 ;
B3 m3 M 3 4 84 336 ;
B4 m4 M 4 2 60 120 .
Проверка:
( B1 B2 B3 B4 ) mod M (280 105 336 120) mod 420
841(mod 420) 1
27
28.
II этап. Представим число AСОК (2, 3, 4, 1) в ПССAПСС ( a1 B1 a2 B2 a3 B3 a4 B4 ) mod M
(2 280 3 105 4 336 1 120) mod 420
(560 315 1344 120) mod 420 2339(mod 420) 239 420 .
Проверка: число AПСС 239 в ПСС представляется в СОК в виде
Aсок 2, 3, 4, 1 .
28













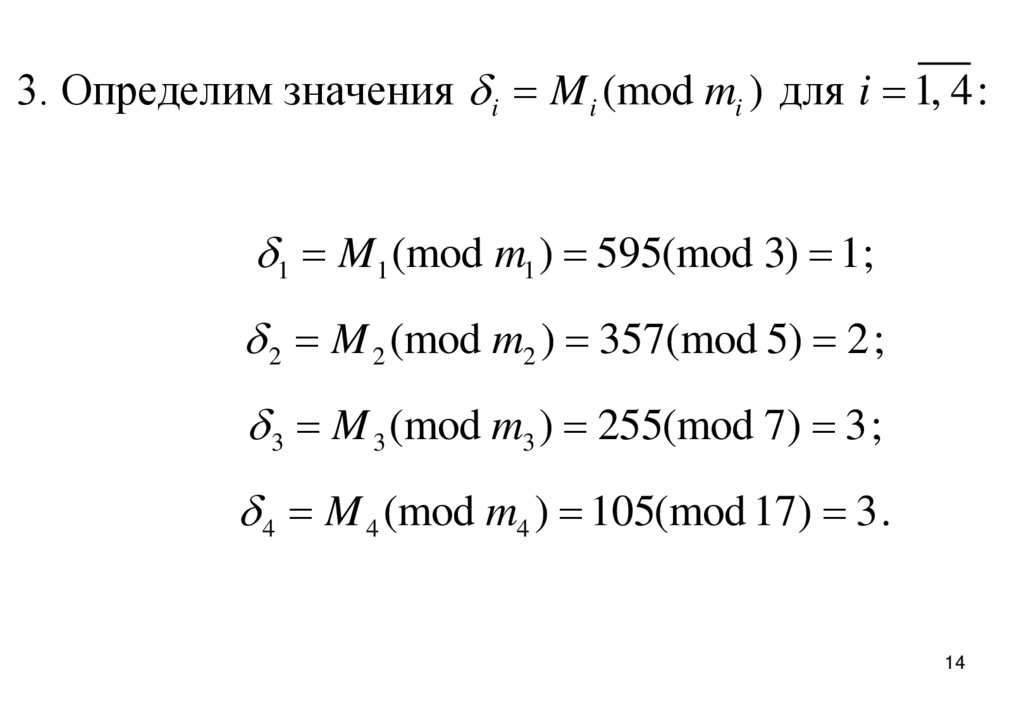

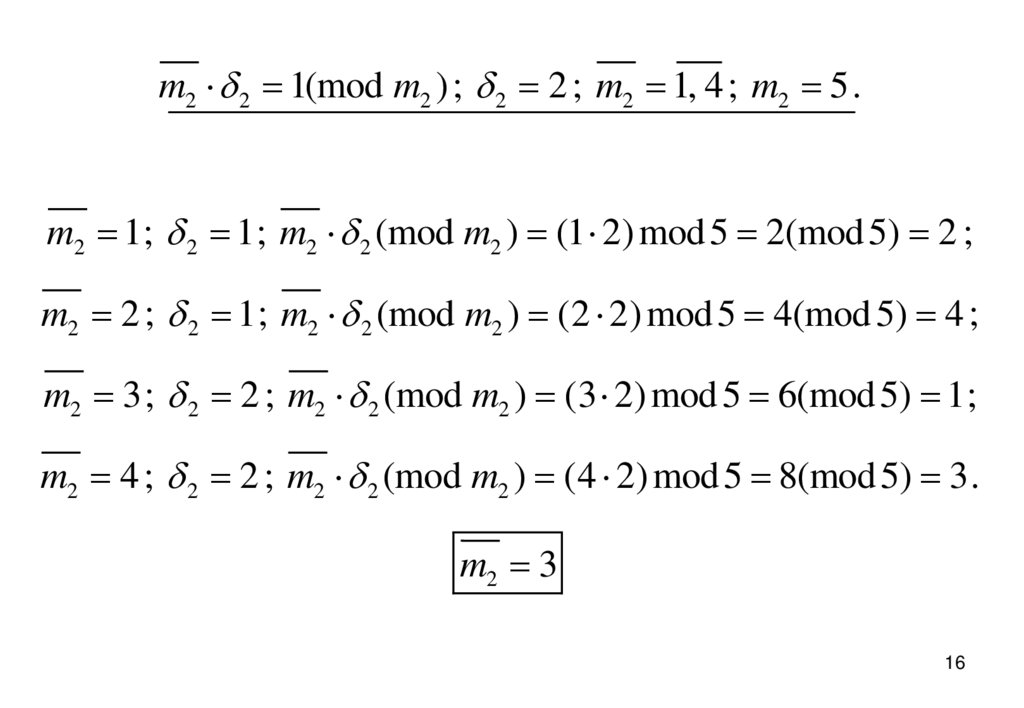








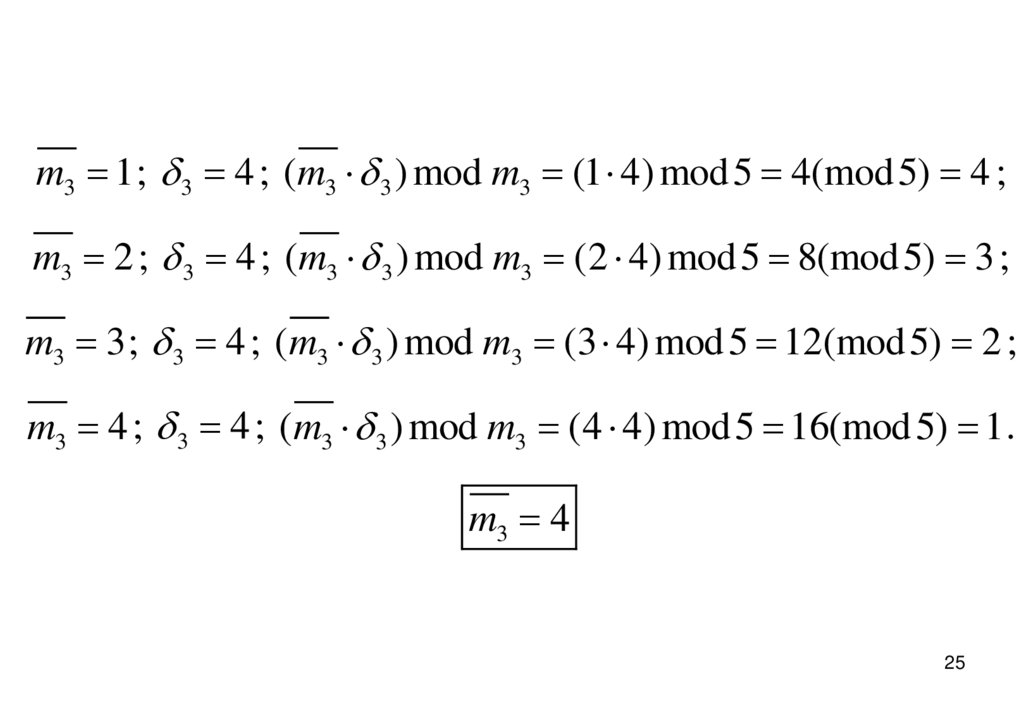



 mathematics
mathematics








