Интерактивный плакат. Четырехугольники

1.

Зуева Татьяна Михайловна, Лузан Елена Юрьевна
Муниципальное
бюджетное общеобразовательное
учреждение «Гимназия №22 г.Белгорода»
Учителя математики
Высшая квалификационная категория

2.

Геометрия, 7 – 9. Учебник для общеобразовательных
учреждений./ Л.С.Атанасян, В.Ф. Бутузов и др.М.:Просвещение, 2010.-384с.
Поурочные разработки по геометрии к учебному
комплекту Л.С.Атанасян и др. 8 класс./Н.Ф.Гаврилова –
М.:ВАКО, 2009.- 368с.
Геометрия 8. Рабочая тетрадь./Ю.А.Глазков и др. –
М.:Просвещение, 2009. – 96с.
Дидактические материалы по геометрии для 8./Б.Г.Зив и
др. – М.:Просещение, 2009. – 144с.
Наглядный справочник по математике для 7-11
классов./Л.Э.Генденштейн. – М.:Илекса, 2010. – 96с.

3.

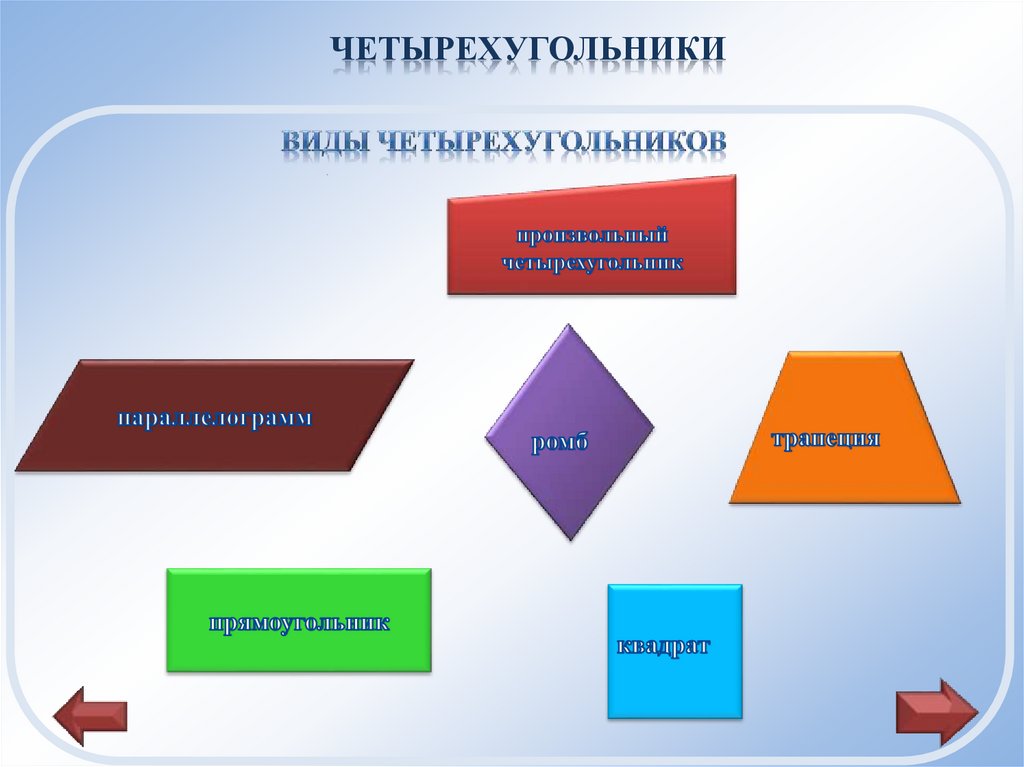
ЧЕТЫРЕХУГОЛЬНИКИ

4.

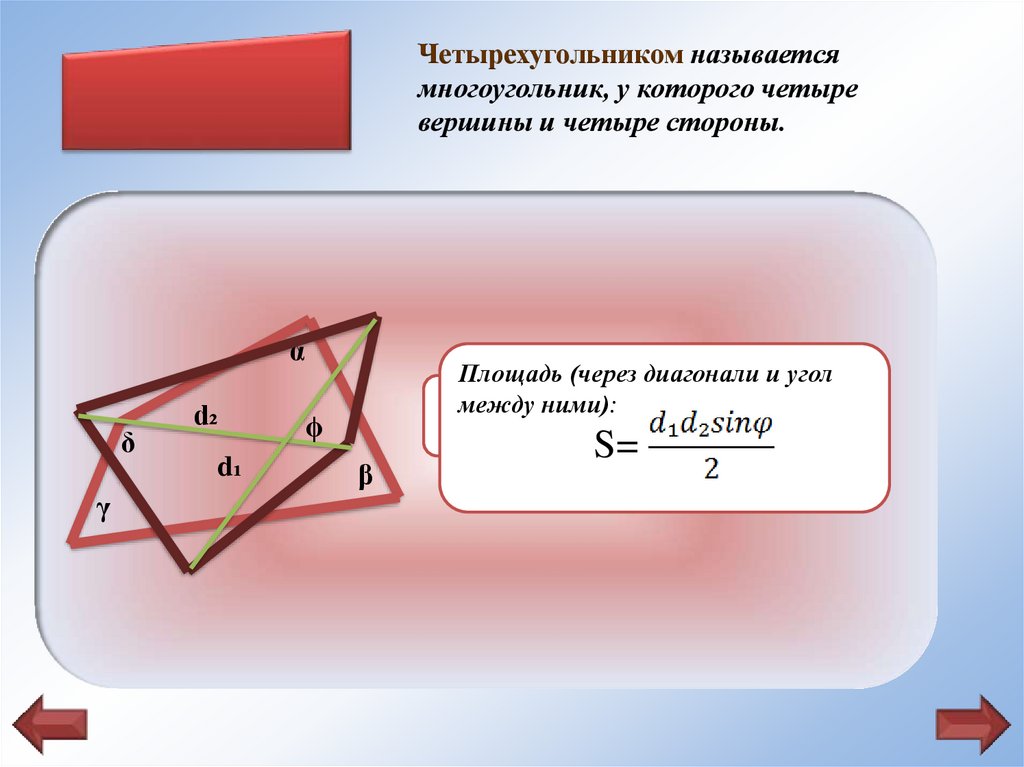
Четырехугольником называется
многоугольник, у которого четыре
вершины и четыре стороны.
α
δ
γ
d₂
d₁
Площадь (через диагонали и угол
Сумма
внутренних
углов равна 360°
между
ними):
α + β + γ + δ =360°.
ϕ
β
S=

5.

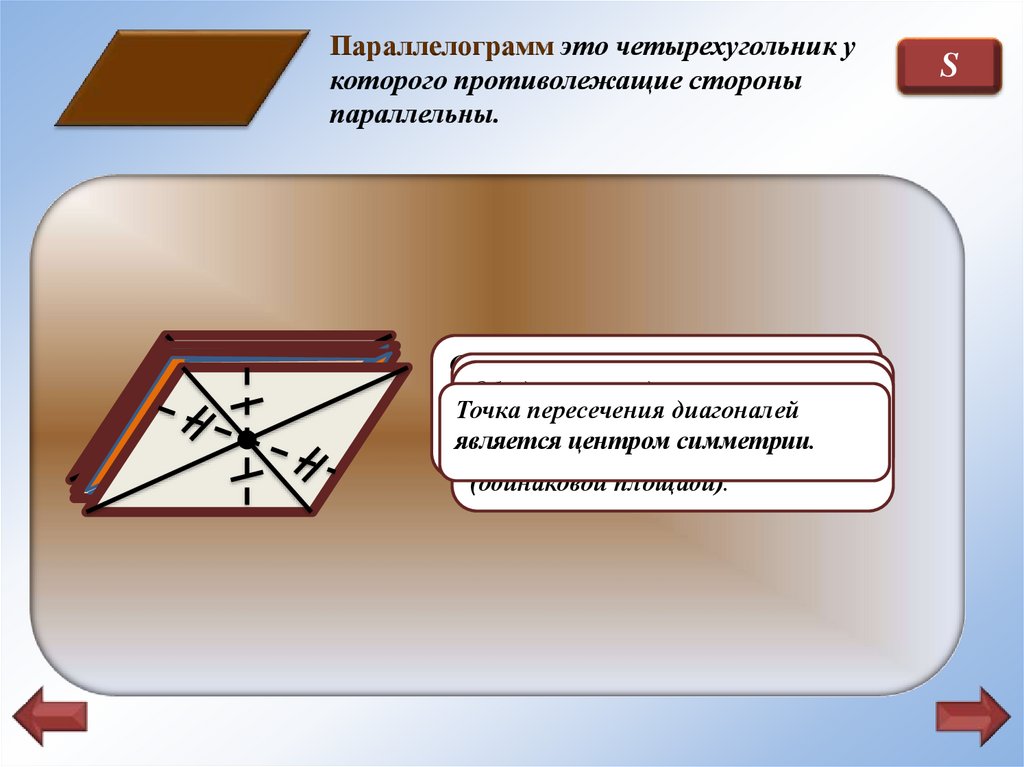
Параллелограмм это четырехугольник у
которого противолежащие стороны
параллельны.
Диагонали
точкой пересечения
Противолежащие
стороны
равны
и
Противолежащие
углы
попарно
равны.
Сумма
углов, прилежащих
к любой
Противолежащие
стороны попарно равны
делятся
пополам.
параллельны.
стороне,
равна 180°.

6.

Параллелограмм это четырехугольник у
которого противолежащие стороны
параллельны.
Сумма квадратов диагоналей равна
Каждая
диагональ делит
Обе диагонали
сумме
квадратовделят
всех сторон:
Точка
пересечения
диагоналей
параллелограмм
два
равных
параллелограмм на
на
четыре
d₁²+d₂²=a²+b²+c²+d².
является
центром
симметрии.
треугольника.
равновеликих
треугольника
(одинаковой площади).
S

7.

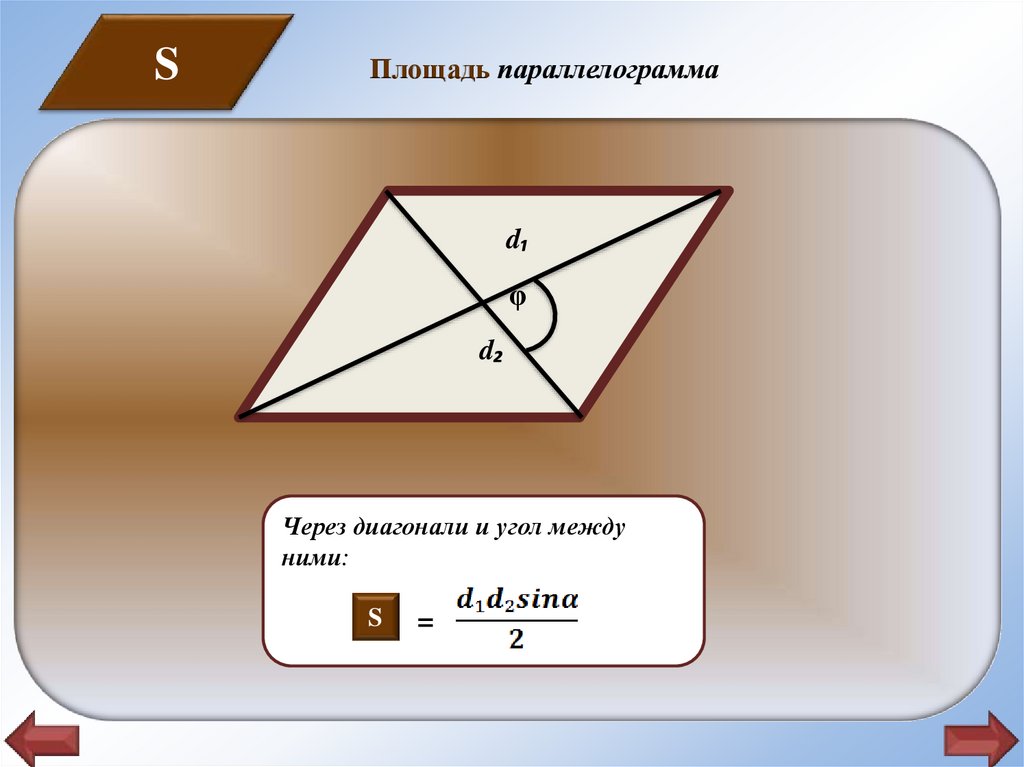
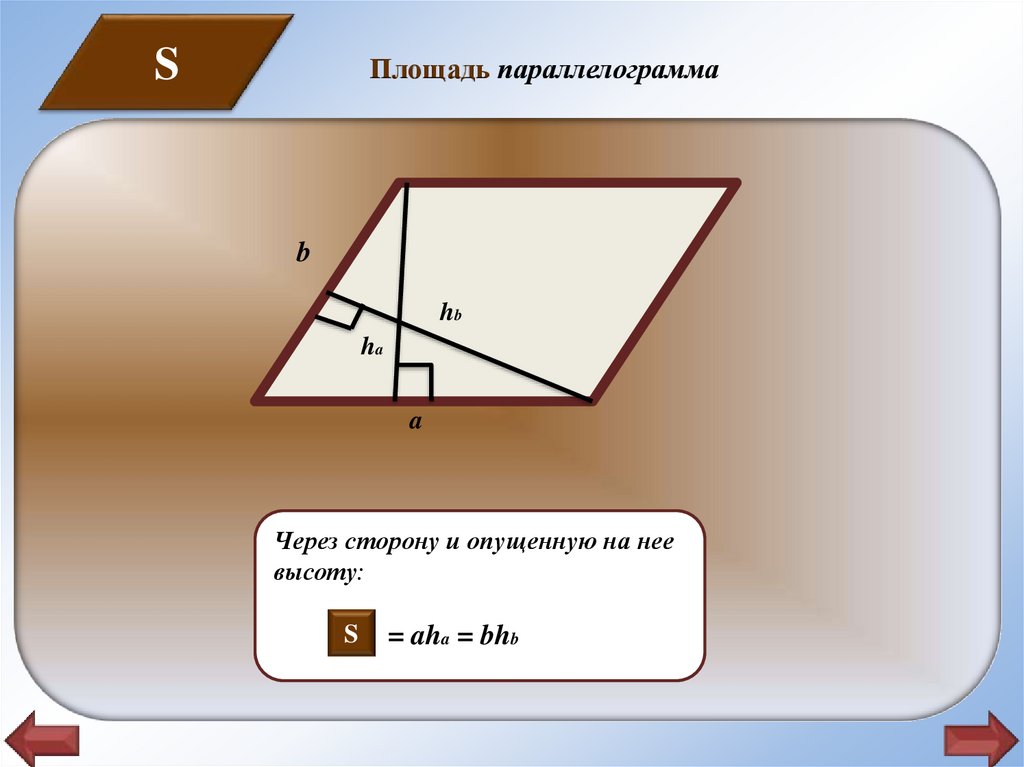
S
Площадь параллелограмма
Через диагонали и угол между ними:
S
=
Через сторону и опущенную на нее
высоту:
S
= aha = bhb
Через две прилежащие стороны и
угол между ними:
S = ab sinα.

8.

S
Площадь параллелограмма
d₁
φ
d₂
Через диагонали и угол между
ними:
S
=

9.

S
Площадь параллелограмма
b
hb
ha
a
Через сторону и опущенную на нее
высоту:
S
= aha = bhb

10.

S
Площадь параллелограмма
b
α
a
Через две прилежащие стороны и
угол между ними:
S
= ab sinα.

11.

Ромб это параллелограмм, у которого
все стороны равны.
Обе
Прямые,
диагонали
содержащие
являются
Все
стороны
равны.
Диагонали
перпендикулярны
и
биссектрисами
диагонали,
являются
внутренних
осями
точкой
пересечения
делятся
углов.
симметрии.
пополам.
S

12.

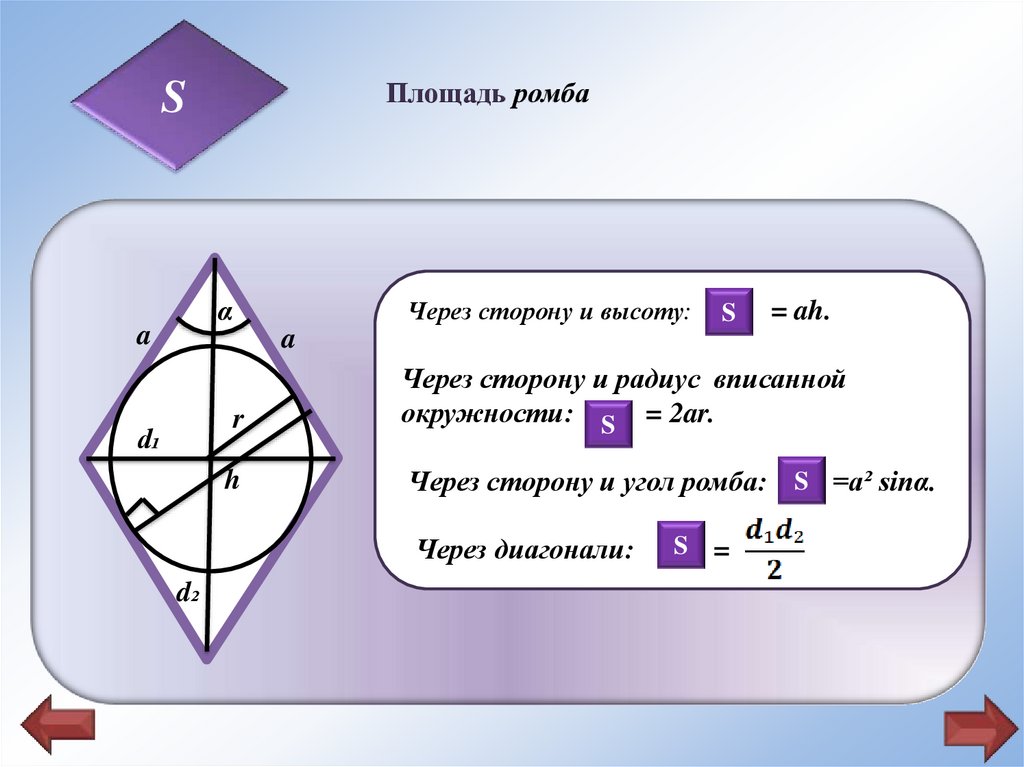
Площадь ромба
S
α
a
Через сторону и высоту: SS
= ah.
a
d₁
r
Через сторону и радиус вписанной
окружности: SS = 2ar.
h
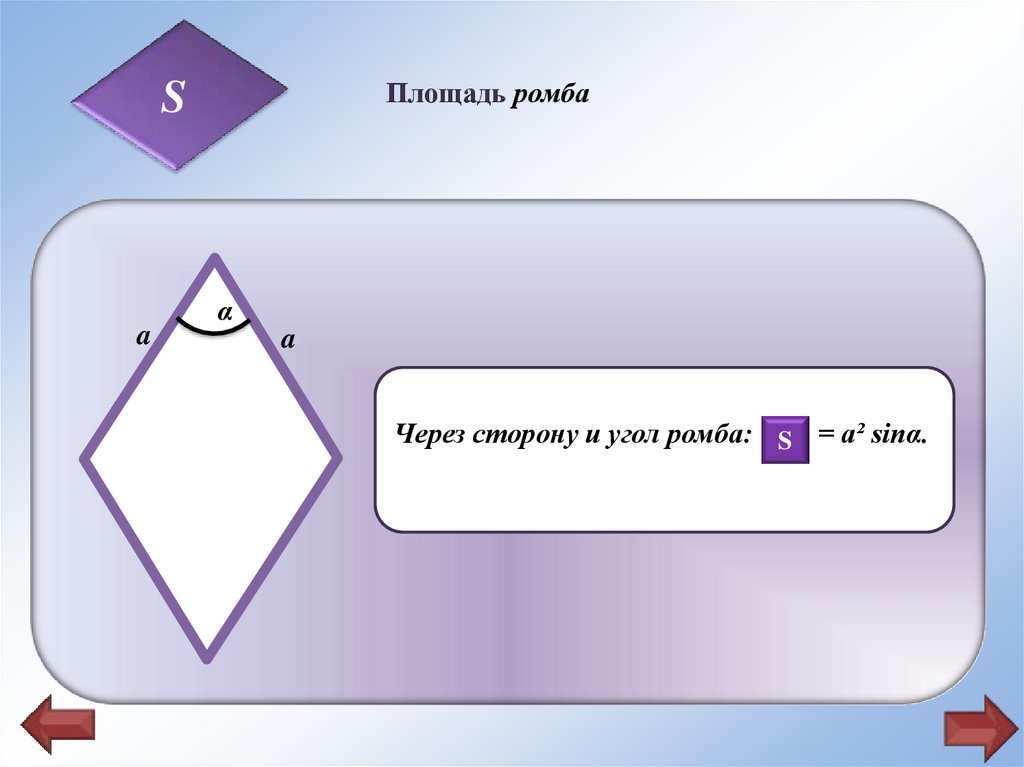
Через сторону и угол ромба: SS =a² sinα.
Через диагонали: SS =
d₂

13.

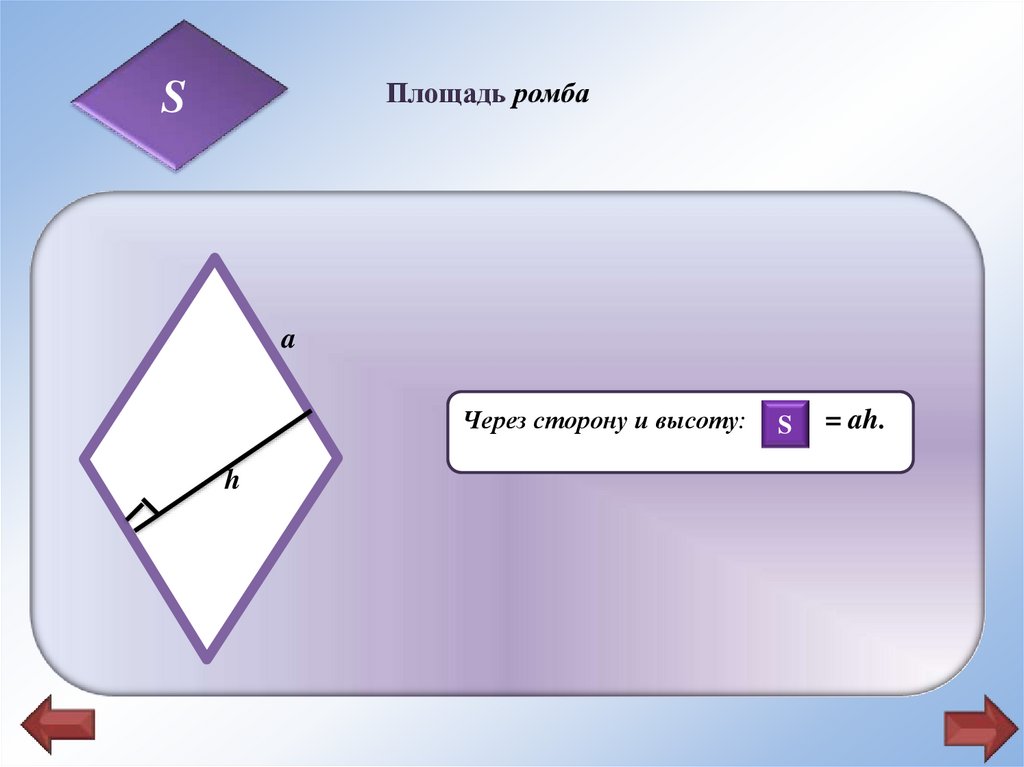
Площадь ромба
S
a
Через сторону и высоту: SS
h
= ah.

14.

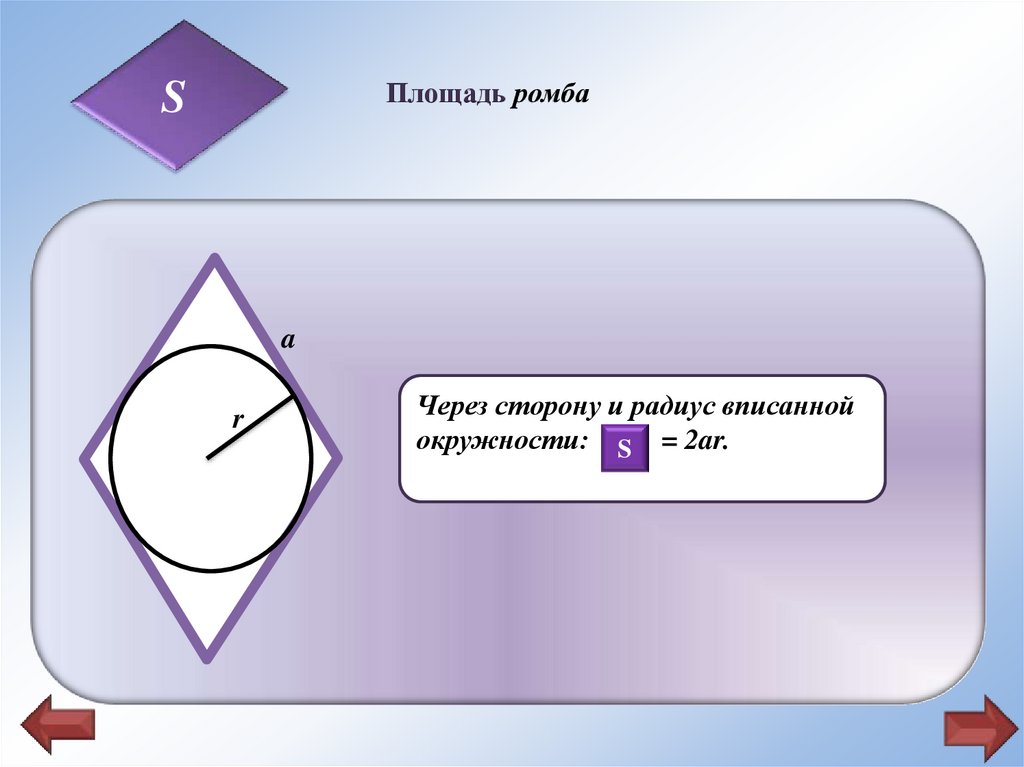
Площадь ромба
S
a
r
Через сторону и радиус вписанной
окружности: SS = 2ar.

15.

Площадь ромба
S
a
α
a
Через сторону и угол ромба: SS = a² sinα.

16.

S
d₁
Площадь ромба
Через диагонали: SS =
d₂

17.

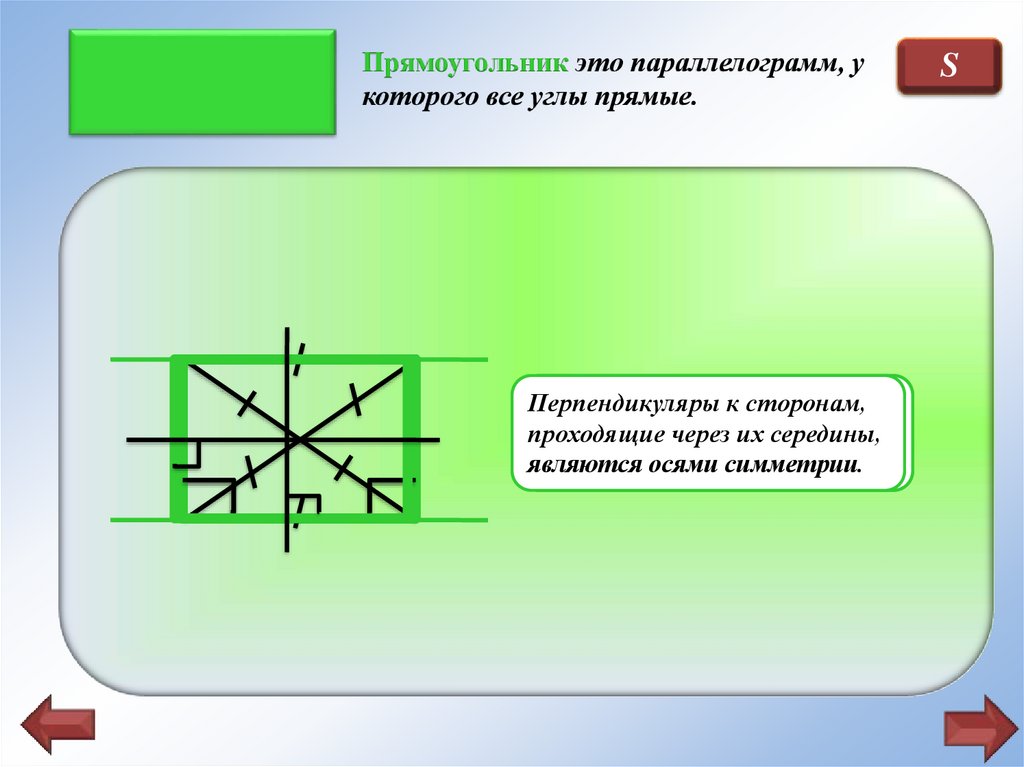
Прямоугольник это параллелограмм, у
которого все углы прямые.
Перпендикуляры
Две стороны
параллельны
кисторонам,
Диагонали
равны
точкой и
проходящие
углы, прилежащие
через
ихк середины,
одной
из
пересечения
делятся
пополам.
являются
этих сторон,
осями
прямые.
симметрии.
S

18.

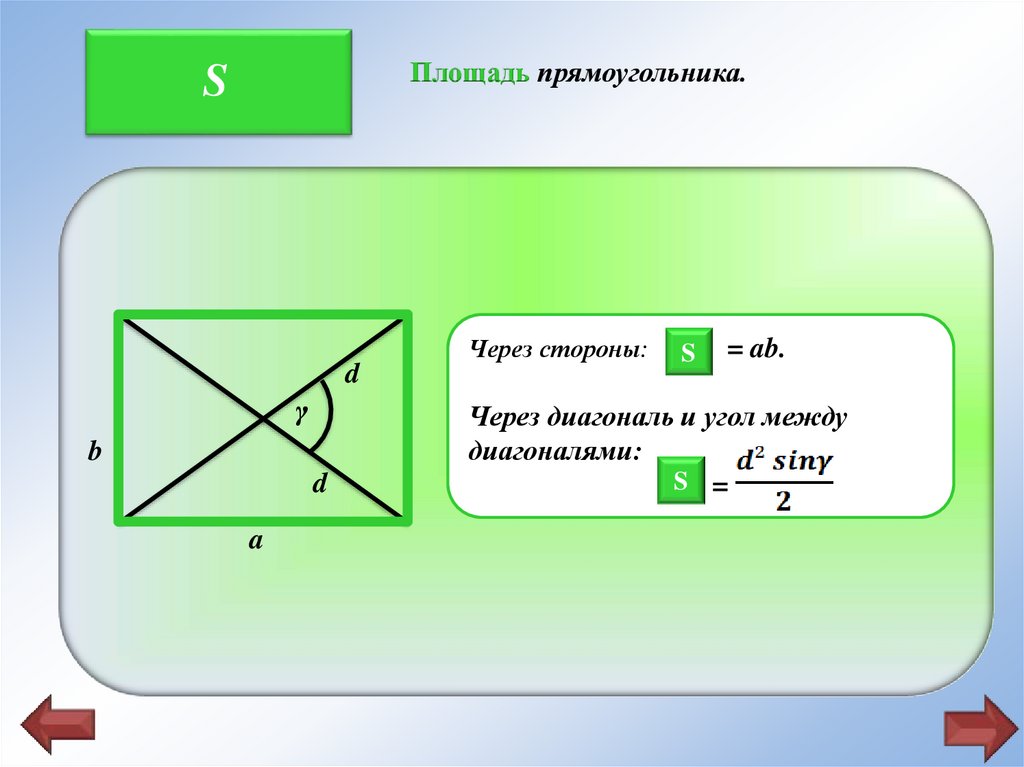
Площадь прямоугольника.
S
d
γ
b
d
a
Через стороны: SS
= ab.
Через диагональ и угол между
диагоналями:
SS =

19.

Площадь прямоугольника.
S
Через стороны: SS
b
a
= ab.

20.

Площадь прямоугольника.
S
d
γ
d
Через диагональ и угол между
диагоналями:
SS =

21.

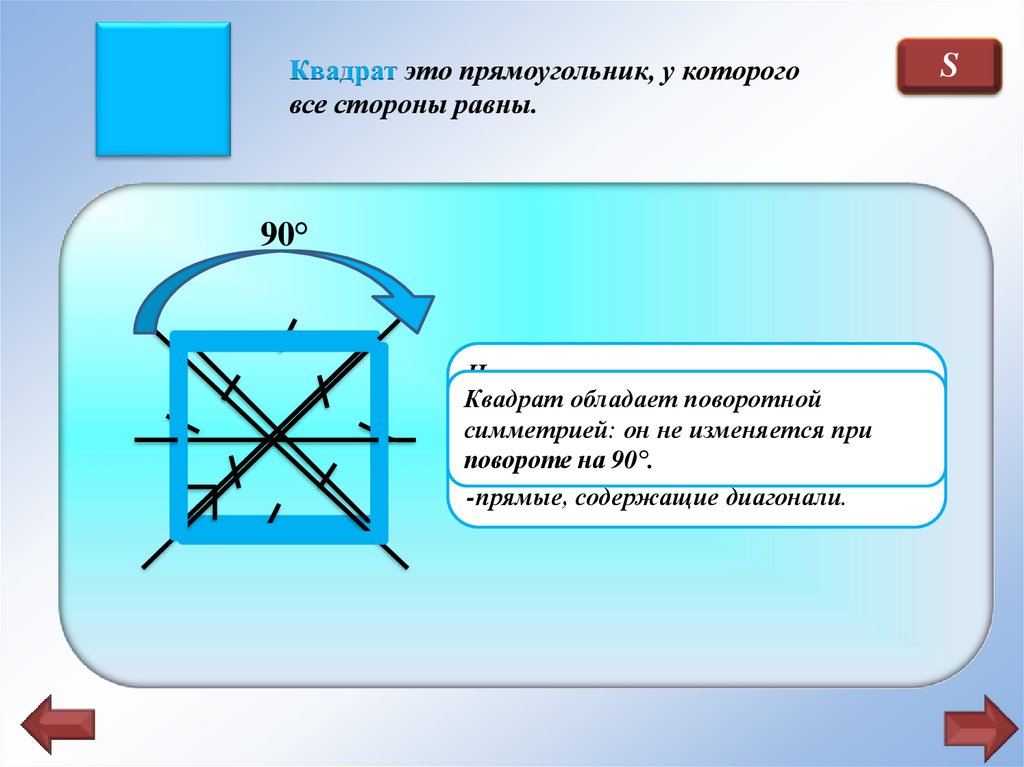
Квадрат это прямоугольник, у которого
все стороны равны.
90°
Четырехугольник имеет четыре оси
Все стороны
равны
и среди
Квадрат
обладает
поворотной
Диагонали
равны, перпендикулярны
и,
симметрии:
внутренних
углов
есть прямой
симметрией:
он не
изменяется
при
пересекаясь,
делятся
пополам.
-прямые,
перпендикулярные
сторонам
угол. на 90°.
повороте
и проходящие
через их середины;
-прямые, содержащие диагонали.
S

22.

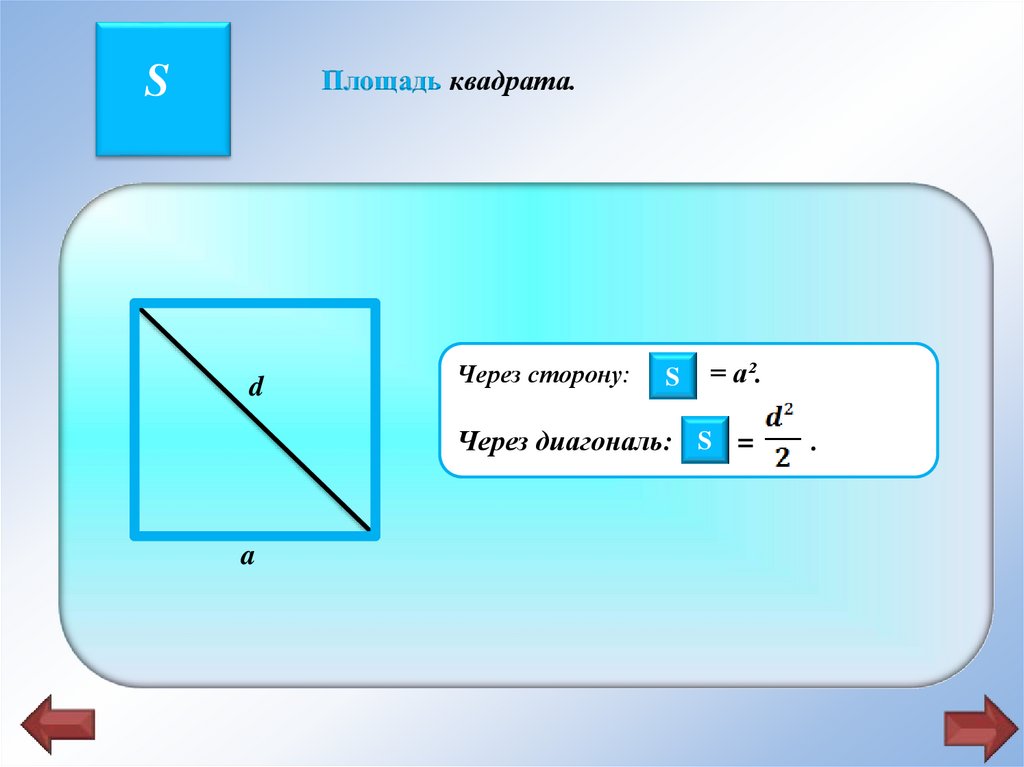
Площадь квадрата.
S
d
Через сторону: SS
= a².
Через диагональ: SS =
a
.

23.

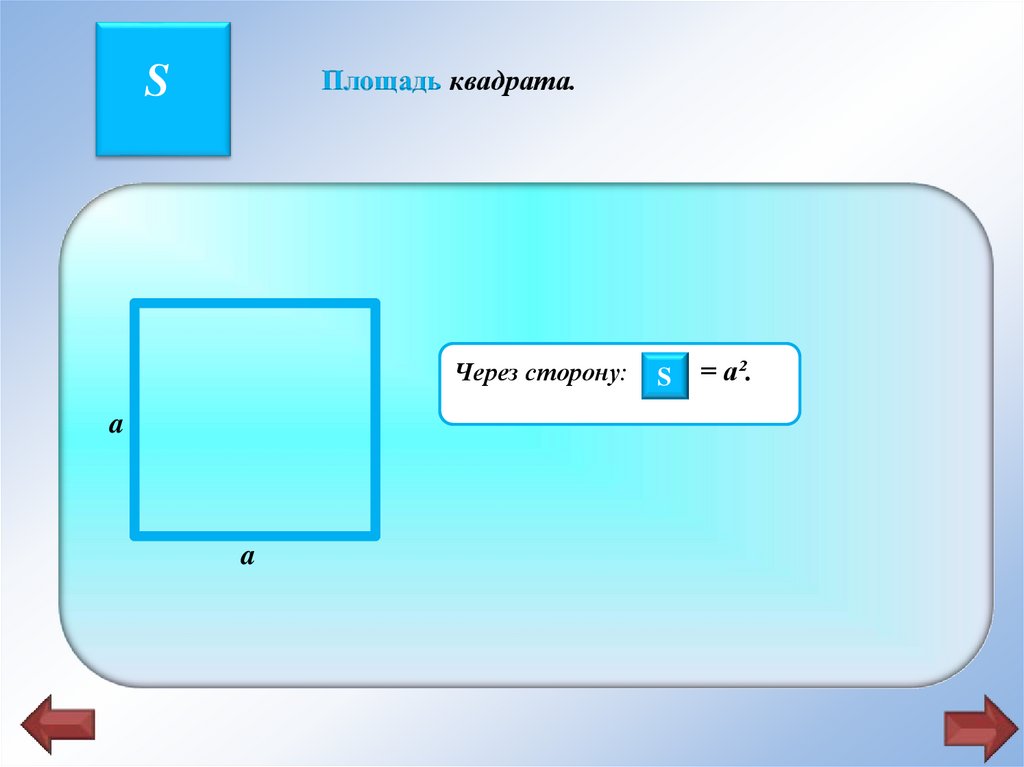
Площадь квадрата.
S
Через сторону: SS
a
a
= a².

24.

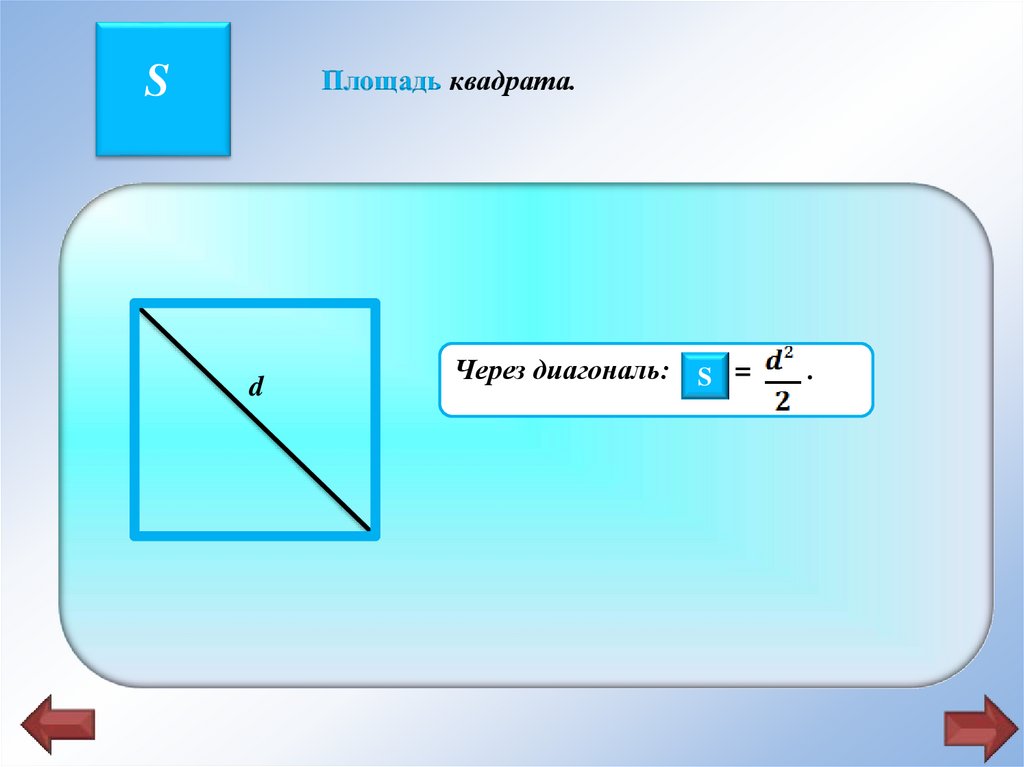
Площадь квадрата.
S
d
Через диагональ: SS =
.

25.

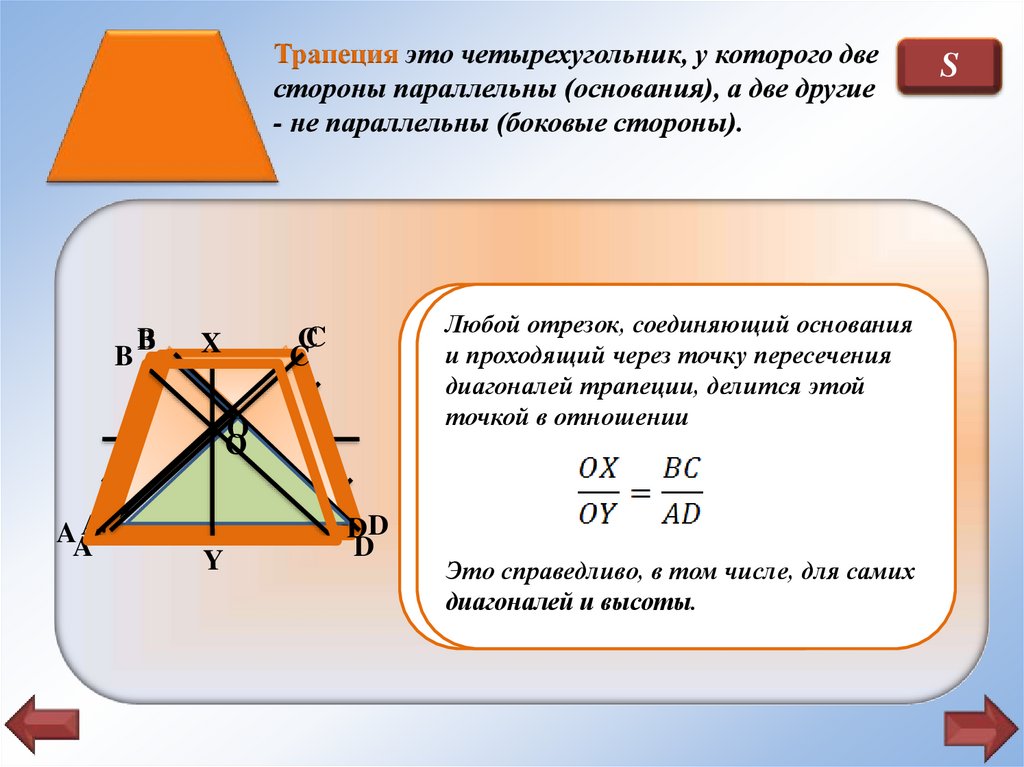
Трапеция это четырехугольник, у которого две
стороны параллельны (основания), а две другие
- не параллельны (боковые стороны).
B
B
X
β
Оγ
CC
C
O
ОО
AAA
α
Щ
Y
δ
DD
D
ТреугольникиAOD
Любой отрезок, соединяющий
и COB,
основания
образованные
и проходящий
основаниями
через
точкуипересечения
Средняя
линия
параллельна
основаниям,
Треугольники
AOB
и DOC.
отрезками
диагоналей
диагоналей,
трапеции,
подобны.
делится
этой
Сумма
углов,
прилежащих
к любой
равна
их полусумме
и делит
любой
Образованные
боковыми
сторонами
Коэффициент
точкойстороне,
вс отношении
подобия
k равен на прямых,
боковой
равна
180°:
концами,
лежащими
и отрезок
отрезками
диагоналей,
отношению
оснований:
содержащих
основания
пополам:
равновелики
(имеют
равные
α + β = 180°,
площади).
= MN
δ =180°.
MN ǁkγa,+
ǁ b, MN=
Отношение
Это справедливо,
площадей
в том
этих
числе, для самих
треугольников
диагоналей и высоты.
равно k².
S

26.

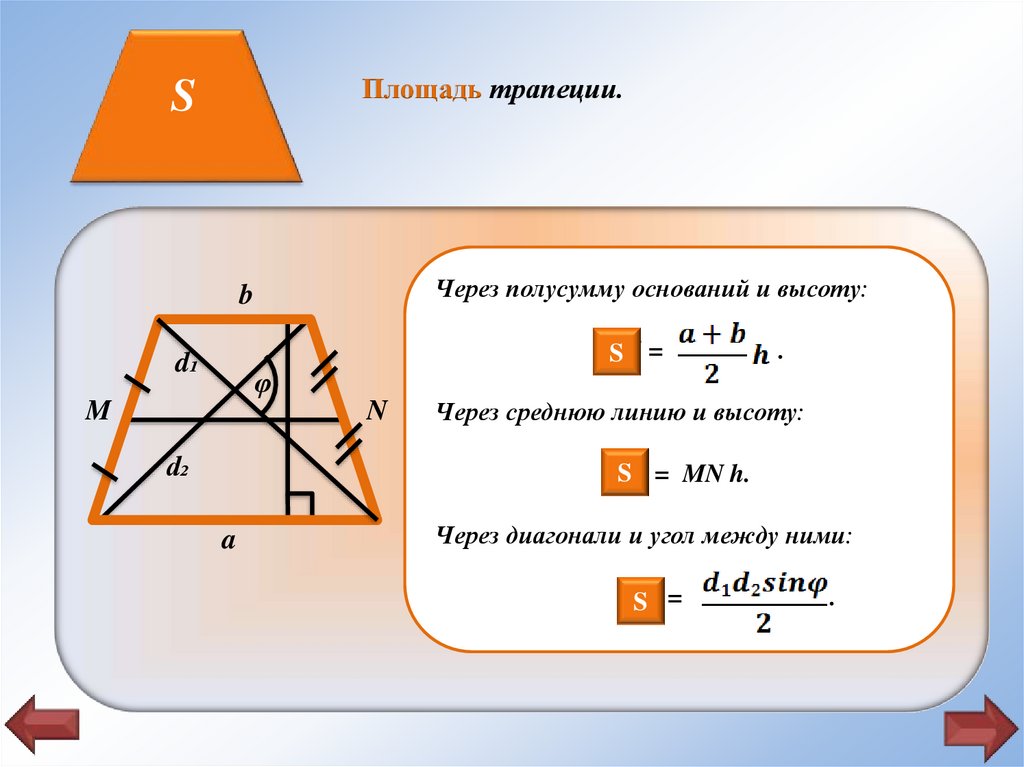
Площадь трапеции.
S
Через полусумму оснований и высоту:
b
SS =
d₁
φ
M
N
d₂
.
Через среднюю линию и высоту:
S S = MN h.
a
Через диагонали и угол между ними:
SS =
.

27.

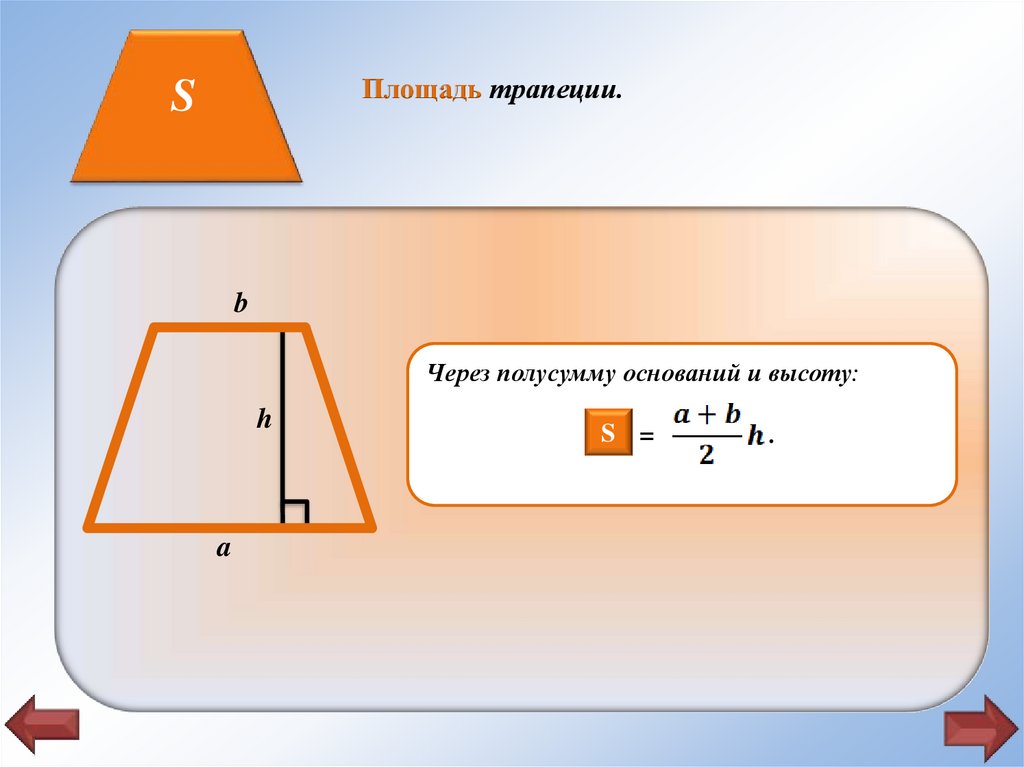
Площадь трапеции.
S
b
Через полусумму оснований и высоту:
h
a
SS =
.

28.

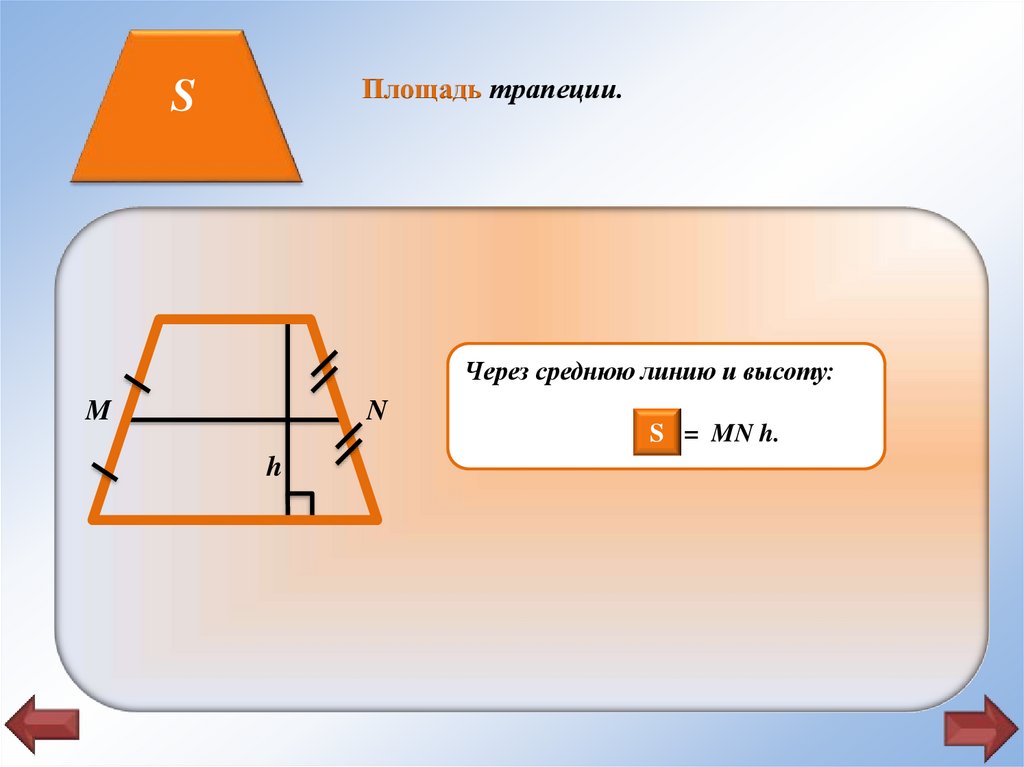
Площадь трапеции.
S
Через среднюю линию и высоту:
M
N
h
SS = MN h.

29.

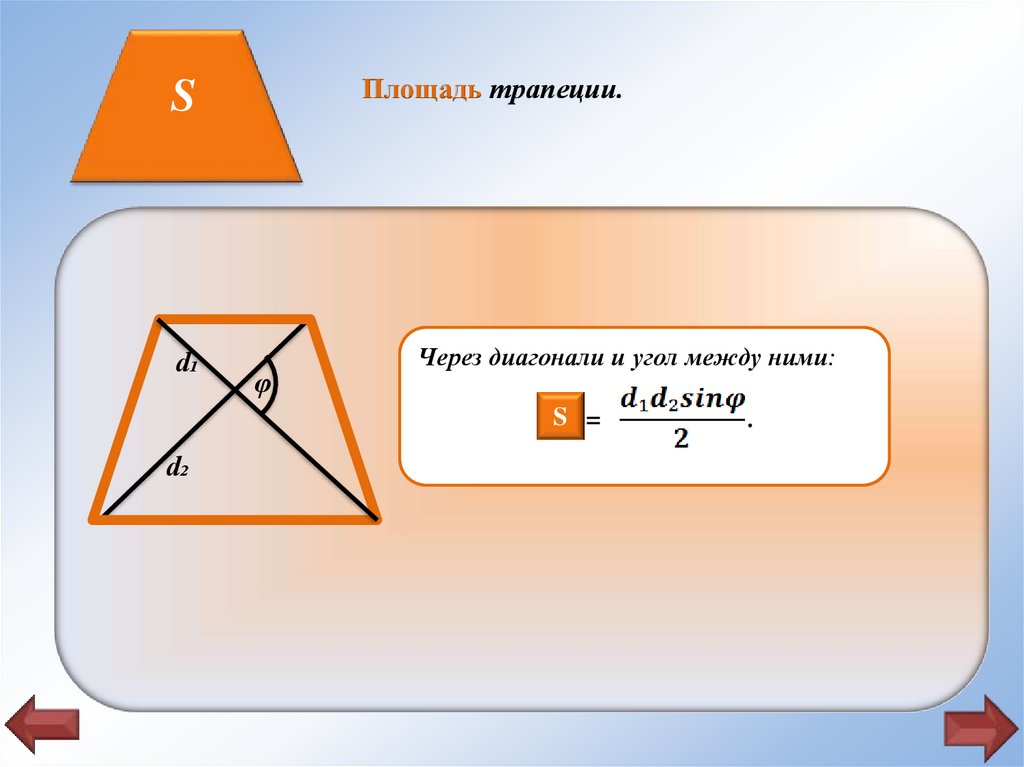
Площадь трапеции.
S
d₁
φ
Через диагонали и угол между ними:
SS =
d₂
.

30.

http://belgym22.ru/ - Сайт МБОУ «Гимназия №22» г.Белгород.
http://4ege.ru/gia-po-matematike/ - Видеоуроки к ЕГЭ.
http://www.it-n.ru/default.aspx - Сеть творческих учителей.
http://karmanform.ucoz.ru/ - Карман для математики.
http://uztest.ru/exam?idexam=1 – Тесты ГИА и ЕГЭ.
http://webmath.exponenta.ru/ax/aj/ta/oly.html - Книжные полки
http://www.it-n.ru/communities.aspx?cat_no=133137&tmpl=com ТРИЗ