Микроструктурные эффекты в порошковой дифракции и методы их описания

1. Микроструктурные эффекты в порошковой дифракции и основные методы их описания

Дифракция нейтронов 2017
Докладчик:
Подчезерцев С.Ю.
15.06.2017
Гатчина

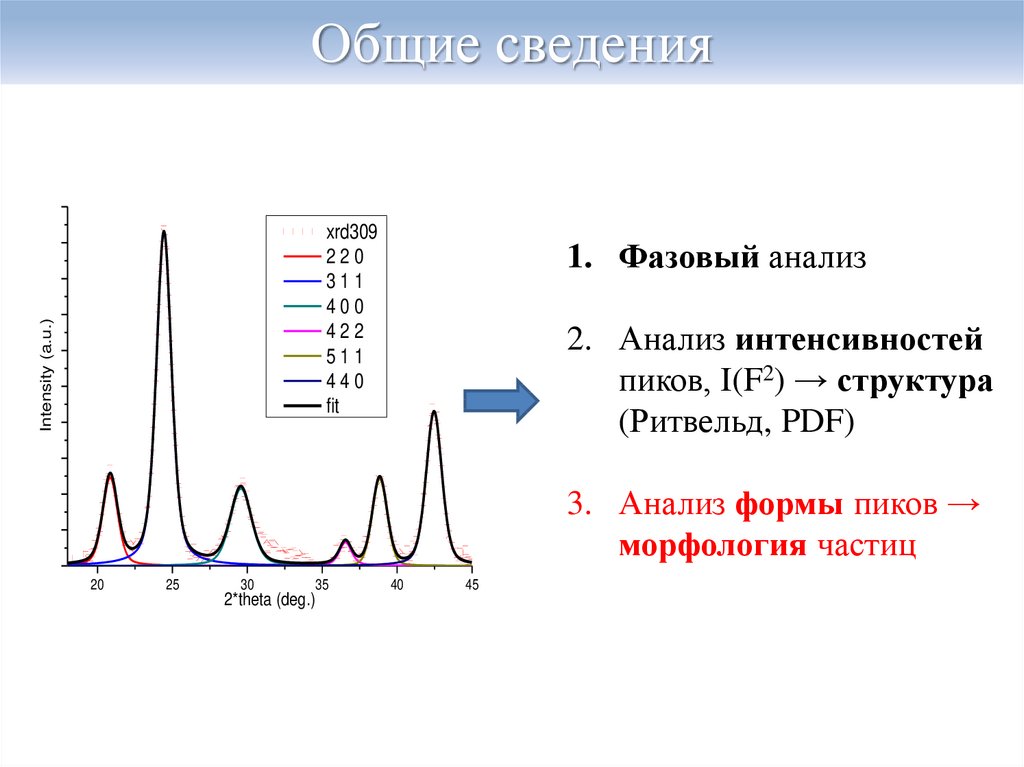
2. Общие сведения

Intensity (a.u.)
xrd309
220
311
400
422
511
440
fit
1. Фазовый анализ
2. Анализ интенсивностей
пиков, I(F2) → структура
(Ритвельд, PDF)
3. Анализ формы пиков →
морфология частиц
20
25
30
2*theta (deg.)
35
40
45

3. Рассеяние на кристаллах конечных размеров

Внутри кристалла
1
Функция формы g (r )
образца
0 За его пределами
G ( s ) FT g (r )
Фурье
образ
G ( s ) FT g (r ) g ( r )
s
автокорреляционной функции:V A (r ) g (u )g (r u )du
2
G ( s ) V FT { As (r )}
2
*
N
2
I (s )
F ( s ) F ( s )
G
(
s
H
)
VVc
H

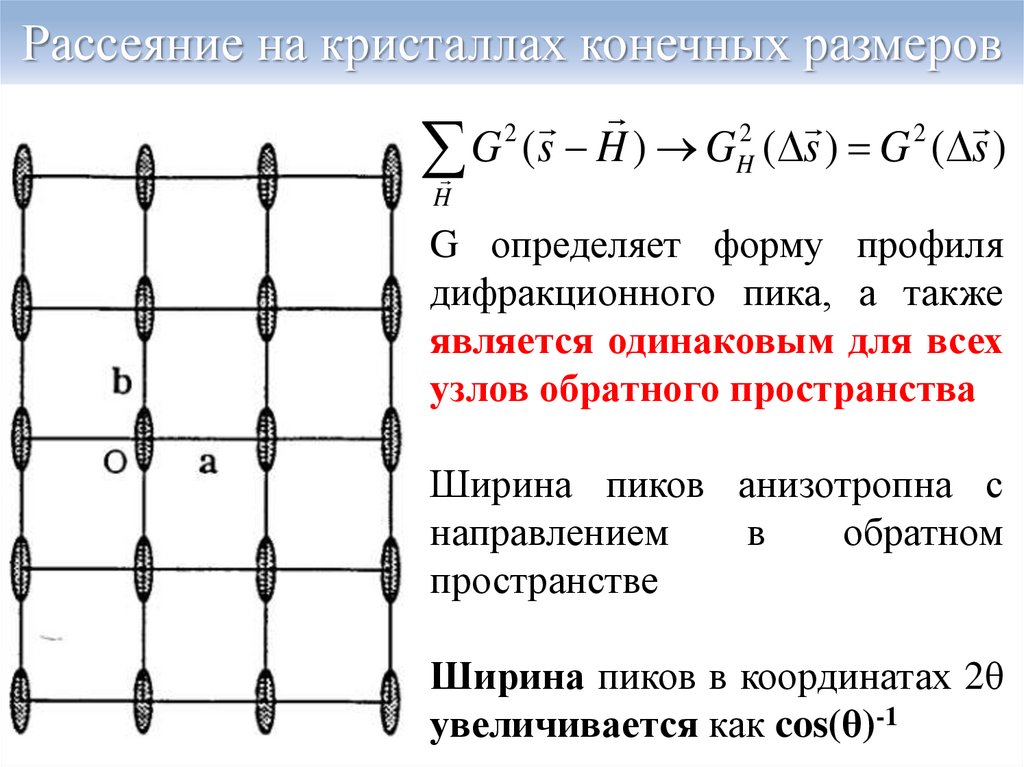
4. Рассеяние на кристаллах конечных размеров

2
2
2
G (s H ) GH ( s ) G ( s )
H
G определяет форму профиля
дифракционного пика, а также
является одинаковым для всех
узлов обратного пространства
Ширина пиков анизотропна с
направлением
в
обратном
пространстве
Ширина пиков в координатах 2θ
увеличивается как cos(θ)-1

5. Рассеяние на реальных кристаллах

Наличие дефектов: средняя структура + структурный
фактор конкретной ячейки
2 is Rn
*
I ( s ) ( Fm Fm n )e
n
m
Fm Fm (s ) структурный фактор m-ой ячейки
pn ( Rn , s ) Fm Fm* n нет зависимости от m, однако есть
зависимость от s
Количество членов во внутренней сумме определяется как
VAs(Rn)/Vc, тогда интенсивность можно переписать как:
V
I (s )
Vc
2
i
s
R
2
i
s
Rn
*
n
As ( Rn ) Fm Fm n e N As ( Rn ) pn ( Rn , s )e
n
n

6. Диффузное рассеяние

Средний структурный фактор
кристалла
F F 1 / N Fm
m
Локальные флуктуации n F Fm
pn F 2 m m* n F 2 n
I ( s ) NF 2 As ( Rn )e 2 is Rn N As ( Rn ) 2 e 2 is Rn
n
NF
VVc
n
2 is Rn
2
G (s H ) N ne
H
IBragg
n
IDiffuse

7. Кристаллы с напряжениями

Для «напряженного» кристалла
структурный фактор m-ой ячейки
Fm Fe
2 is u m
2 is ( u m u m n )
Определим AD ( Rn , s ) e
2 is Rn
2
Тогда интенсивность I ( s ) NF As ( Rn ) AD ( Rn , s )e
n
Если s=H+Δs рассеянная вокруг брегговского пика
интенсивность:
2 is Rn
2
I ( s ) NFH As ( Rn ) AD ( Rn , s )e
n
размер
деформации

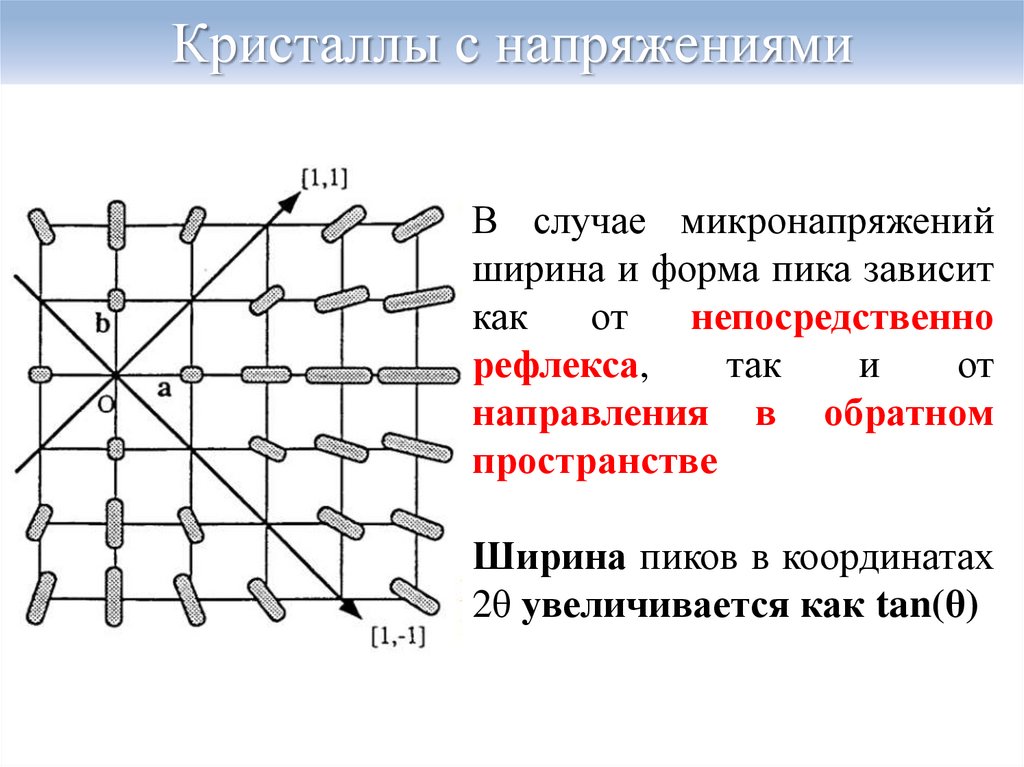
8. Кристаллы с напряжениями

В случае микронапряжений
ширина и форма пика зависит
как
от
непосредственно
рефлекса,
так
и
от
направления в обратном
пространстве
Ширина пиков в координатах
2θ увеличивается как tan(θ)

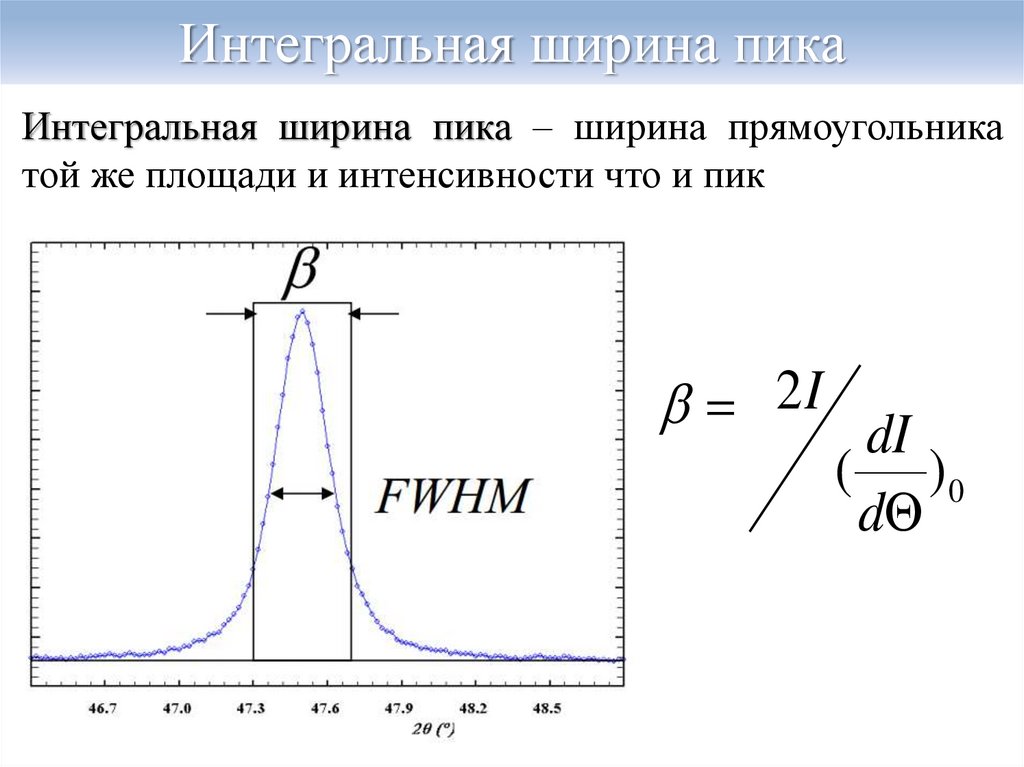
9. Интегральная ширина пика

Интегральная ширина пика – ширина прямоугольника
той же площади и интенсивности что и пик
2 I dI
( )0
d

10. Формула Шеррера

K hkl
DS
(2 ) cos 0
D – шерреровский размер
высота колонки из ЭЯ вдоль
направления hkl
K – константа Шеррера, имеет
зависимость от hkl и сингонии
D
5 nm
Ds ≠D
Не учтены никакие иные причины уширения пиков, кроме размерного
Но:
Ширина пиков с увеличением 2θ возрастает как cos-1θ

11. Формула Стокса-Уилсона

Деформационное уширение дифракционных пиков
2d sin
d
2 cos n
d d
def 2 ctg
d
tg
d
Уравнение Стокса-Уилсона.
ε – стоксовские микронапряжения.
Не понятен физический смысл уширения
Но:
Ширина пиков с увеличением 2θ возрастает как tanθ

12. Метод Уильямсона-Холла

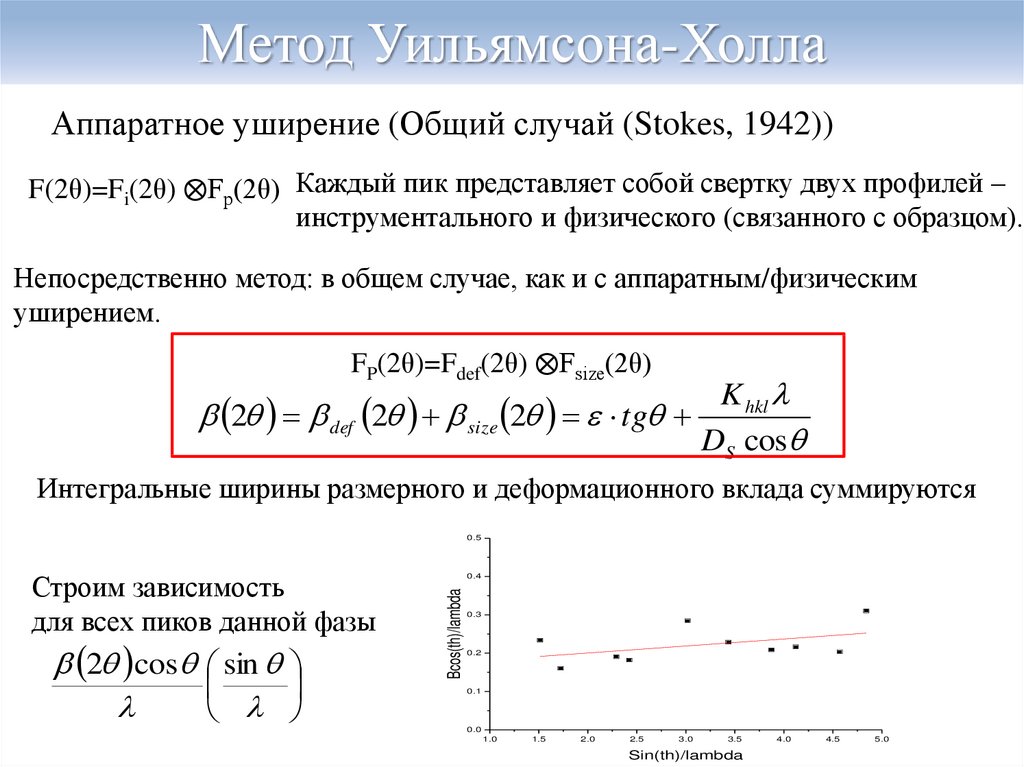
Аппаратное уширение (Общий случай (Stokes, 1942))
F(2θ)=Fi(2θ) ⨂Fp(2θ) Каждый пик представляет собой свертку двух профилей –
инструментального и физического (связанного с образцом).
Непосредственно метод: в общем случае, как и с аппаратным/физическим
уширением.
FP(2θ)=Fdef(2θ) ⨂Fsize(2θ)
2 def 2 size 2 tg
K hkl
DS cos
Интегральные ширины размерного и деформационного вклада суммируются
0.5
2 cos sin
0.4
Bcos(th)/lambda
Строим зависимость
для всех пиков данной фазы
0.3
0.2
0.1
0.0
1.0
1.5
2.0
2.5
3.0
3.5
Sin(th)/lambda
4.0
4.5
5.0

13. Метод Уоррена-Авербаха

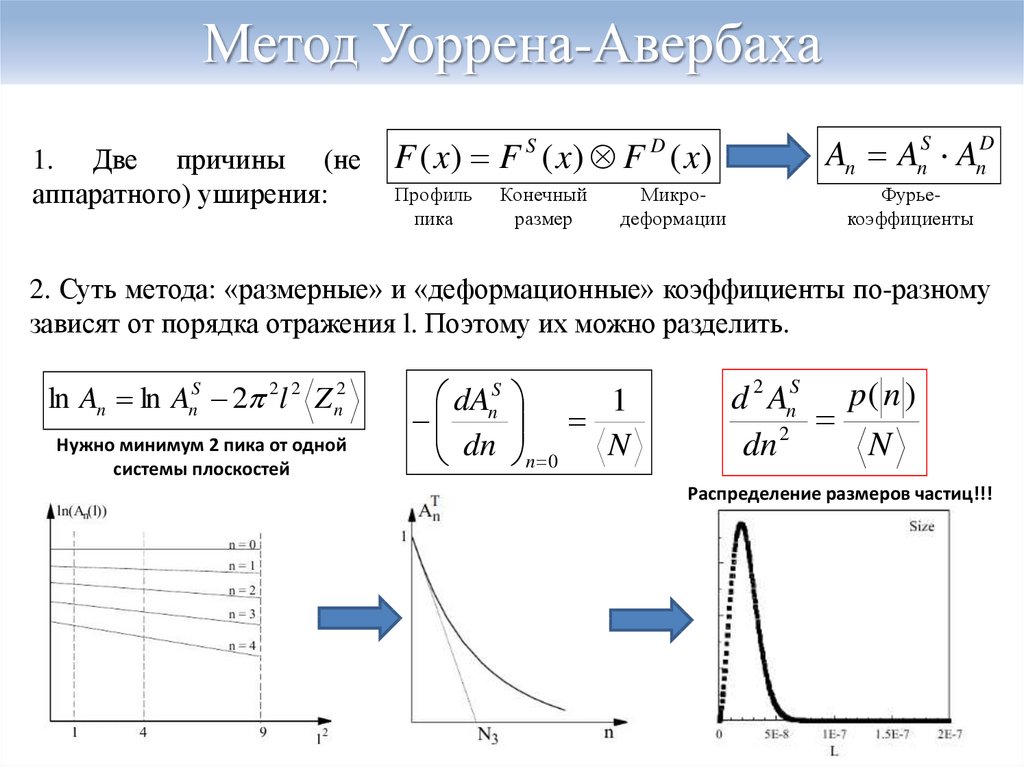
1. Две причины (не
аппаратного) уширения:
F ( x) F S ( x) F D ( x)
Профиль
пика
Конечный
размер
Микродеформации
An AnS AnD
Фурьекоэффициенты
2. Суть метода: «размерные» и «деформационные» коэффициенты по-разному
зависят от порядка отражения l. Поэтому их можно разделить.
ln An ln AnS 2 2l 2 Z n2
Нужно минимум 2 пика от одной
системы плоскостей
dAnS
dn
1
N
n 0
d 2 AnS p( n )
2
dn
N
Распределение размеров частиц!!!

14. Метод Ритвельда

Расчетная модель порошкового профиля задается выражением
yci I h (Ti Th ) bi
h
Профильная функция характеризуется
значением FWHM, а также параметрами
формы
Свертка аппаратного и физического
уширения

15. Параметры Кальотти

IG
H (U (1 ) D ( D )) tan V tan W
cos 2
2
G
2
2
ST
2
[Y F ( z )]
H L ( X DST ( D )) tan
cos
Принято считать, что гауссиан описывает аппаратное уширение, а
лоренциан физическое,
однако это не всегда так
U, αD, X – характеризуют микронапряжения
Y, IG, αz – характеризуют размер кристаллитов

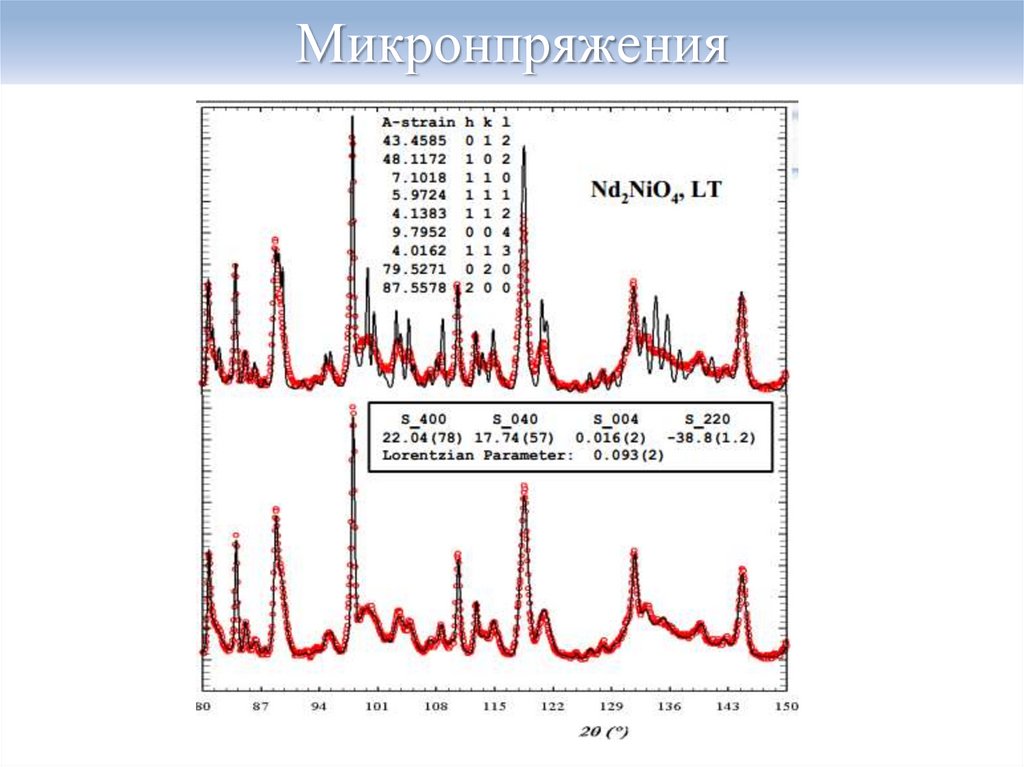
16. Микронапряжения

Возможные причины наличия микронапряжений в
образцах:
• Неоднородные искажения ЭЯ
• Дислокации
• Antiphase domains boundaries (перевод?)
• Эффекты на границах зерен
• Дефекты упаковки
• Неоднородность твердых растворов
• Влияние теплового фактора

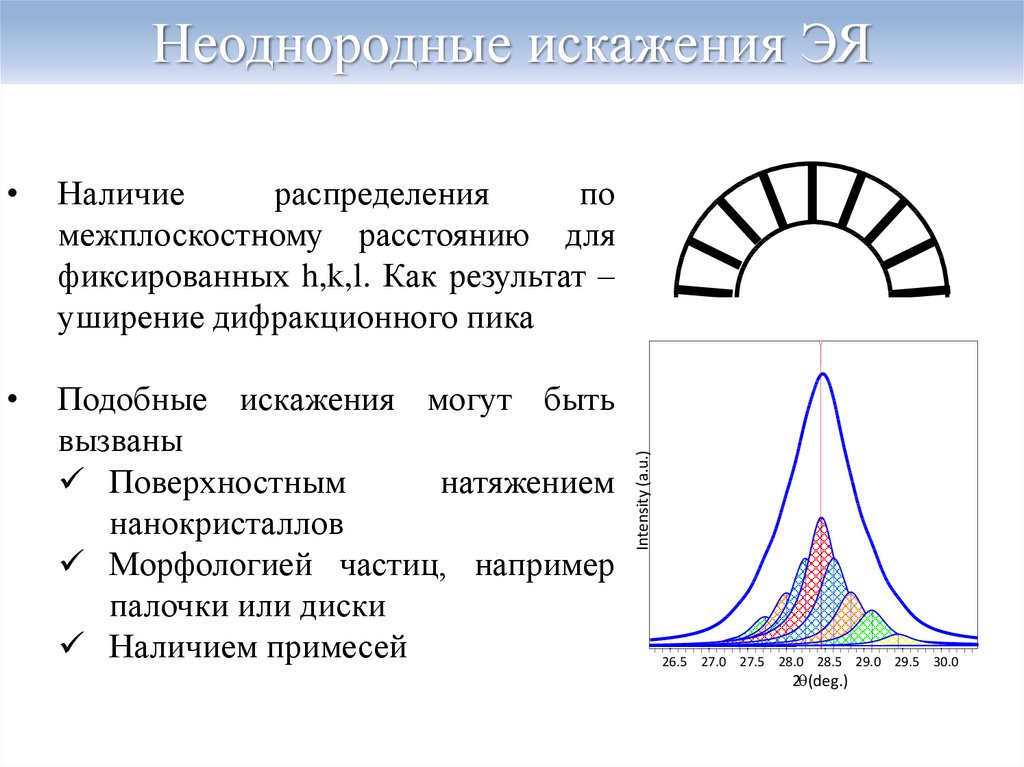
17. Неоднородные искажения ЭЯ

Наличие
распределения
по
межплоскостному расстоянию для
фиксированных h,k,l. Как результат –
уширение дифракционного пика
Подобные искажения могут быть
вызваны
Поверхностным
натяжением
нанокристаллов
Морфологией частиц, например
палочки или диски
Наличием примесей
Intensity (a.u.)
Неоднородные искажения ЭЯ
26.5 27.0 27.5 28.0 28.5 29.0 29.5 30.0
2 (deg.)

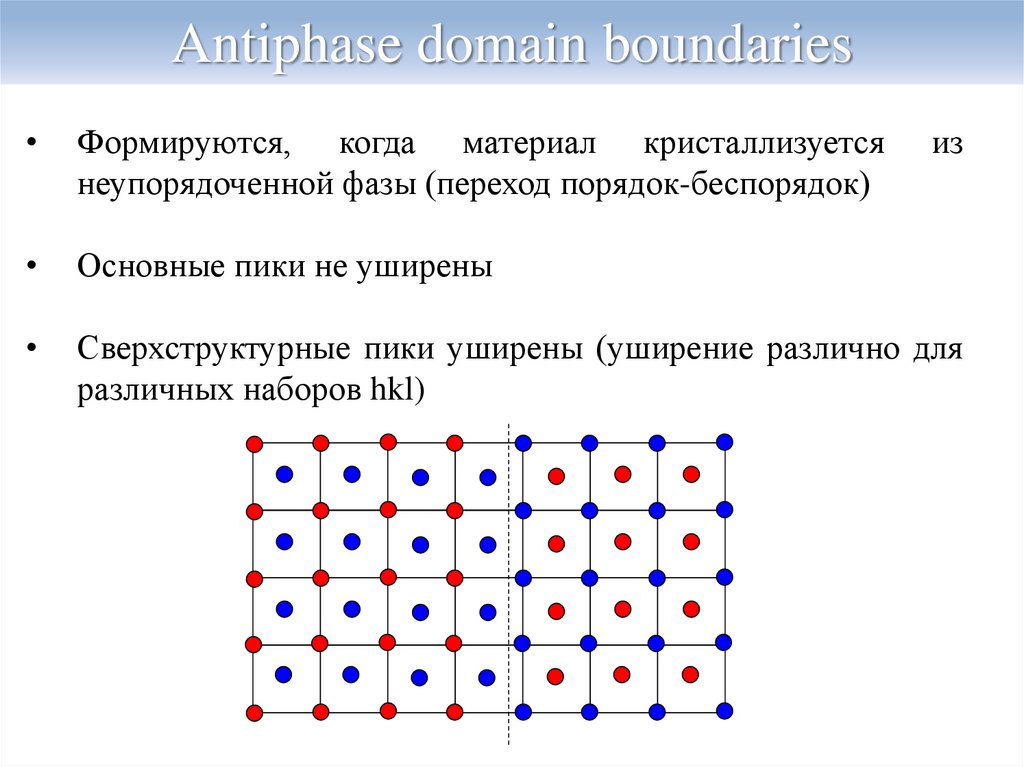
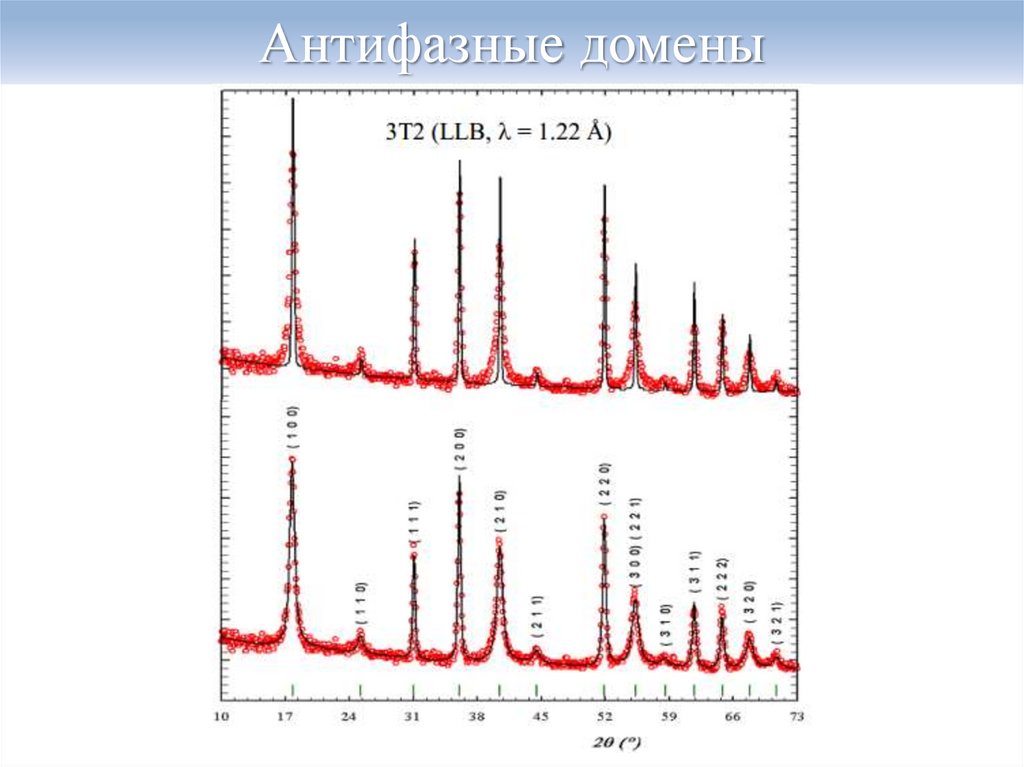
18. Antiphase domain boundaries

Формируются, когда материал кристаллизуется
неупорядоченной фазы (переход порядок-беспорядок)
Основные пики не уширены
Сверхструктурные пики уширены (уширение различно для
различных наборов hkl)
из

19. Дислокации

Линии уширяются т.к. распространение дислокаций имеет
hkl зависимость
Профиль является лоренцевским
Могут быть определены с помощью метода УорренаАвербаха
• Измерение нескольких порядков отражений
• Фурье коэффициенты будут иметь независящий от
размерного эффекта член и член зависящий от
напряжений

20. Дефекты упаковки

Уширение, связанное с наличием дефектов упаковки и
двойникованием будет сворачиваться с размерным Фурье
коэффициентом
• Размерный Фурье коэффициент определенный по
методу Уоррена-Авербаха содержит в себе вклады как от
размера частицы, так и от дефектов упаковки
• Вклад дефектов упаковки hkl-зависим, в то время, как
размерный вклад hkl-независим (в случае изотропных
частиц)
• Вклад дефектов упаковки варьируется, как hkl
зависимая функция кристаллической структуры образца

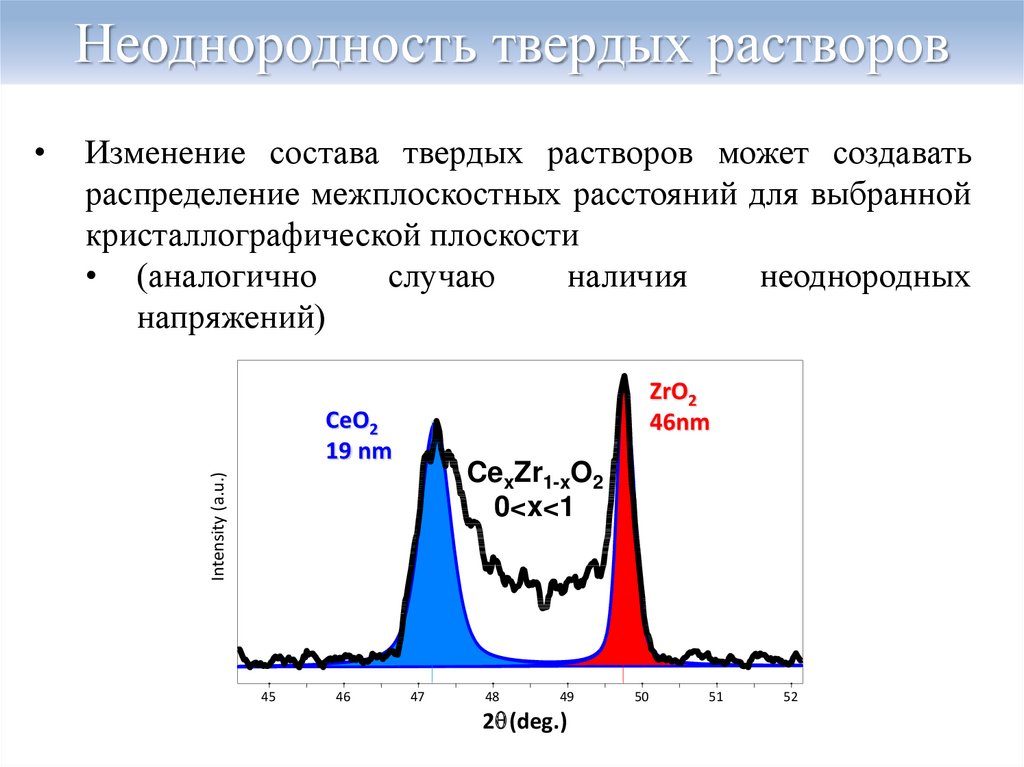
21. Неоднородность твердых растворов

Изменение состава твердых растворов может создавать
распределение межплоскостных расстояний для выбранной
кристаллографической плоскости
• (аналогично
случаю
наличия
неоднородных
напряжений)
ZrO2
46nm
CeO2
19 nm
CexZr1-xO2
0<x<1
Intensity (a.u.)
45
46
47
48
49
2 (deg.)
50
51
52

22. Тепловой фактор

Фактор Дебая-Валлера описывает осцилляцию атомов
вокруг их средней позиции в ячейке
Осцилляция атомов вокруг положения равновесия
приводит к перераспределению интенсивности пика из
максимума в «хвосты»
• Это не увеличивает FWHM пика, но увеличивает
интегральную ширину
Тепловой фактор растет с увеличением угла дифракции
Тепловой фактор должен быть свернут со структурной
амплитудой для каждого пика
• Различные атомы имеют различные тепловые факторы
• Каждый пик содержит различный вклад от атомов
кристалла
F f exp M
X / 3
M 2
d
2
2

23. Феноменологическая модель микронапряжений

Для любого выбранного рефлекса можно записать
1 / d M hkl Ah Bk Cl Dhk Ehl Fhk
2
2
2
2
A…F – метрические параметры обратной ячейки
Каждое зерно будет иметь свой набор A…F, отличный от <A>… <F>
Для удобства переобозначим A…F в αi, и положим что αi имеют гауссово
распределение, характеризуемое ковариантной матрицей
Cij ( i ai )(( j a j )
Дисперсия M
( M hkl )
2
Cii 2 ( i )
M M
(M hkl ) Cij
i j
i, j
2
S
H
HKL
HKL
H K L 4
K L
h k l D
ST
2
( M hkl )
180
8
2
10 8 ln 2(
)
2
M hkl

24. Феноменологическая модель микронапряжений

25. Феноменологическая модель микронапряжений

Выбор модели – два флажка в .pcr файле

26. Учет размеров зерен

27. Учет размеров зерен

28. Учет размеров зерен

29. Учет размеров зерен

30. Учет размеров зерен

Выбор модели только вручную!
Страница 119
FullProf manual

31. Стратегия

1. Необходим ли учет микроструктуры?
Нет?
2. Определение инструментальных параметров
3. Какова физическая причина уширений?
4. Выбор микроструктурной модели
U, V, W

32. Примеры

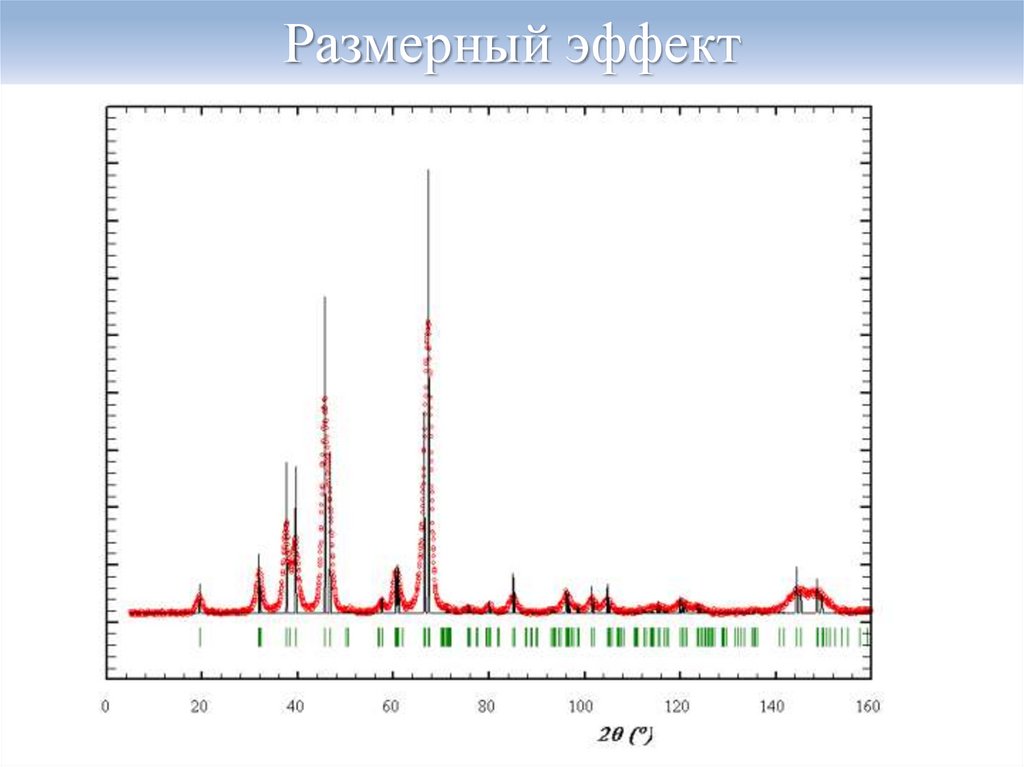
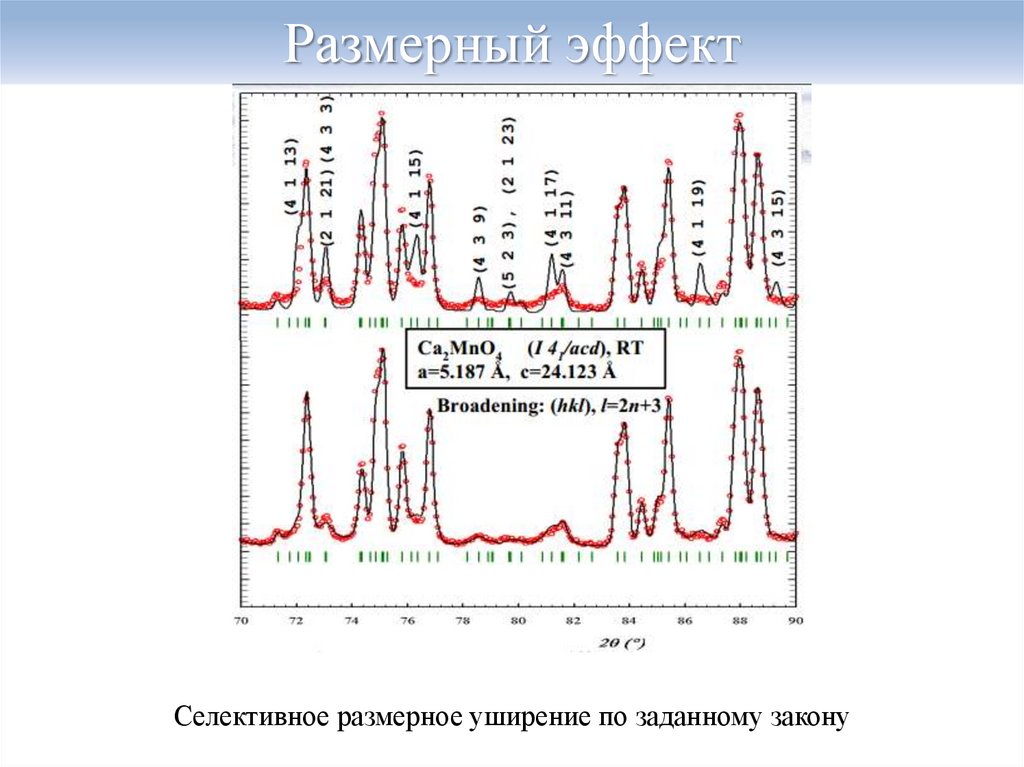
33. Размерный эффект

34. Размерный эффект

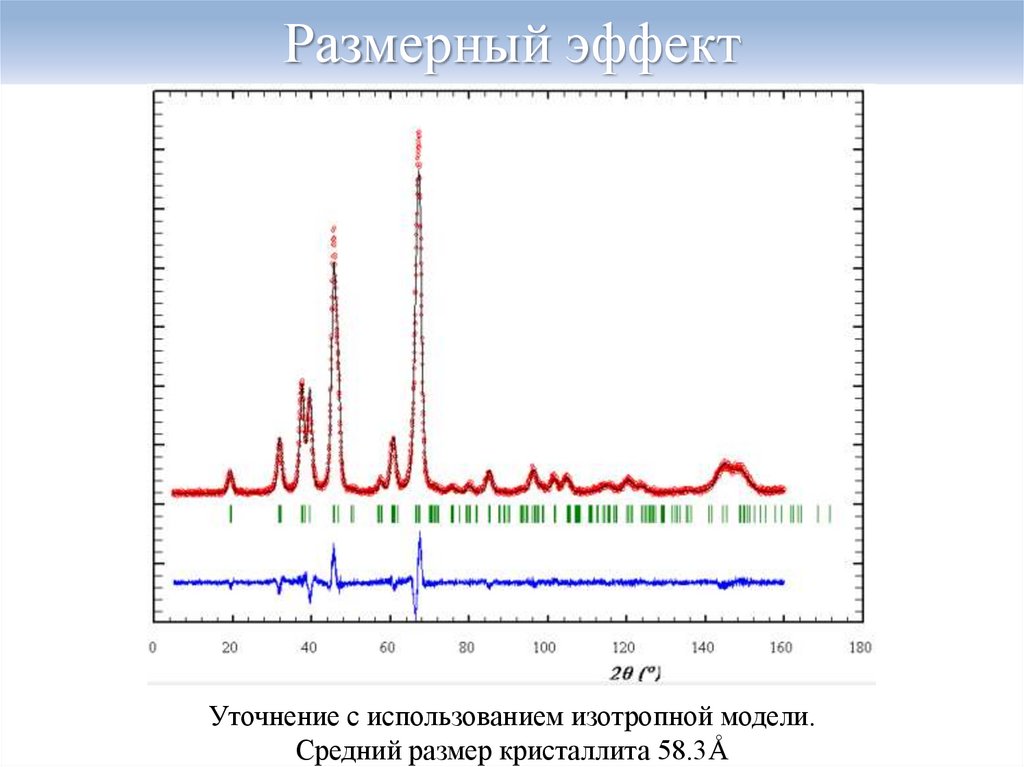
Уточнение с использованием изотропной модели.
Средний размер кристаллита 58.3Å

35. Размерный эффект

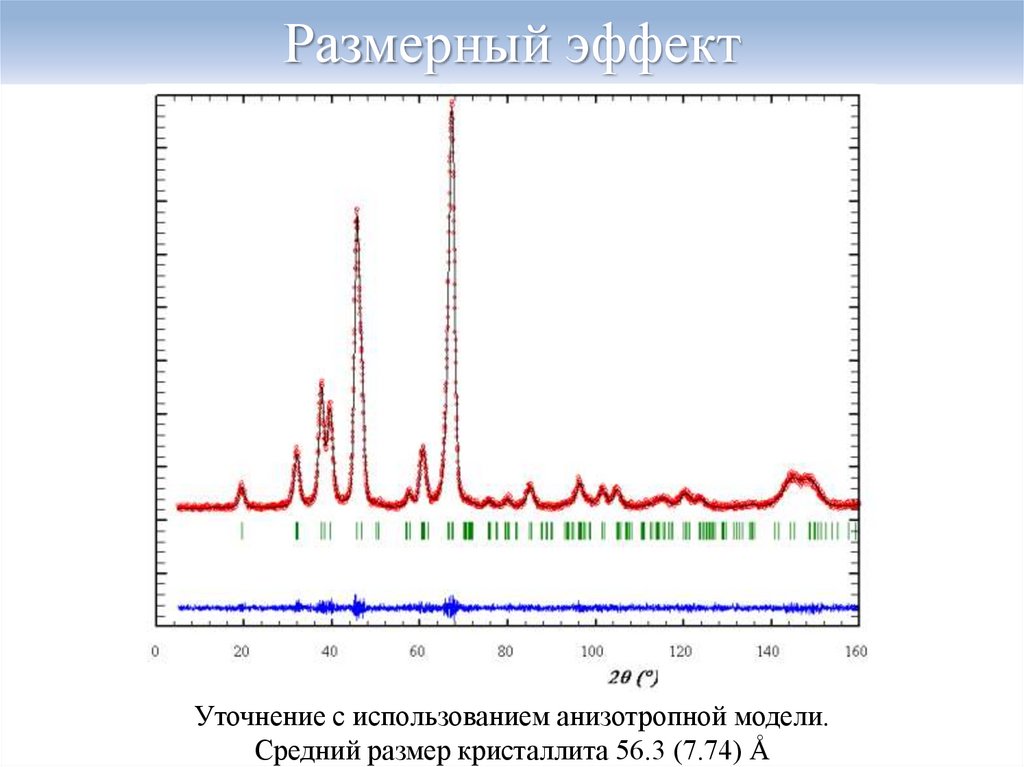
Уточнение с использованием анизотропной модели.
Средний размер кристаллита 56.3 (7.74) Å

36. Размерный эффект

Селективное размерное уширение по заданному закону

37. Микронпряжения

38. Антифазные домены

39. Спасибо за внимание!