Моделирование точности работы БИНС в контуре беспилотного ЛА

1. Дипломная работа

«Моделирование точности работы БИНС в
контуре беспилотного ЛА»
Дипломант: Арыкова А. Ю.
Руководитель работы: профессор Костюков В. М.

2.

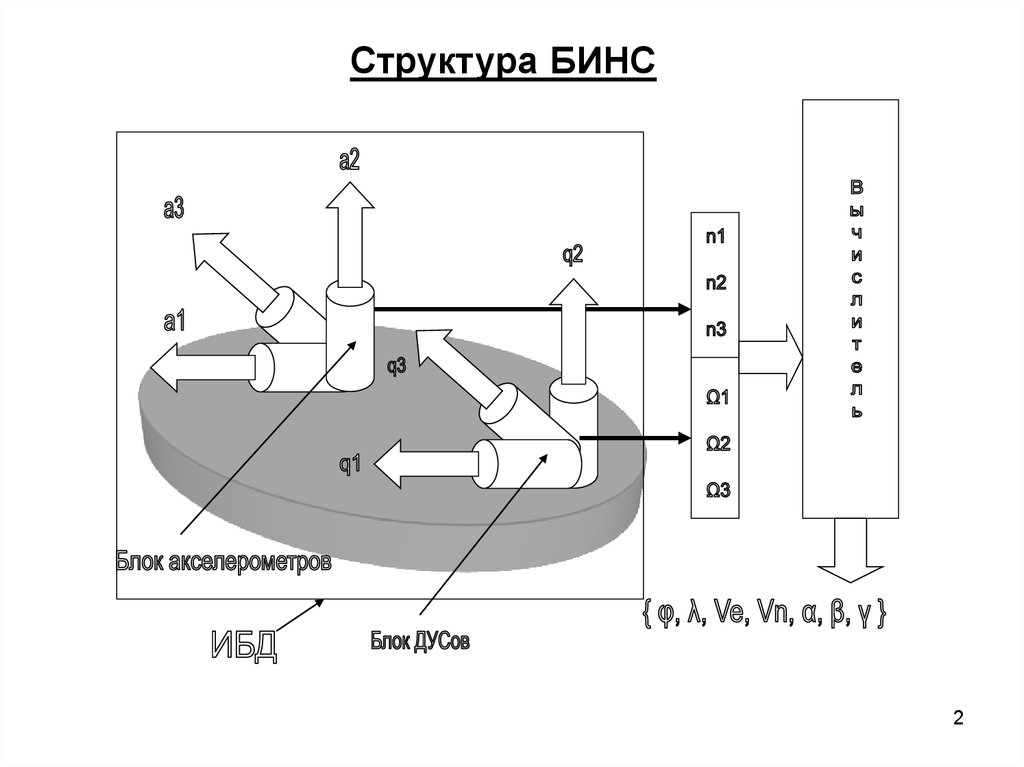
Структура БИНС
2

3.

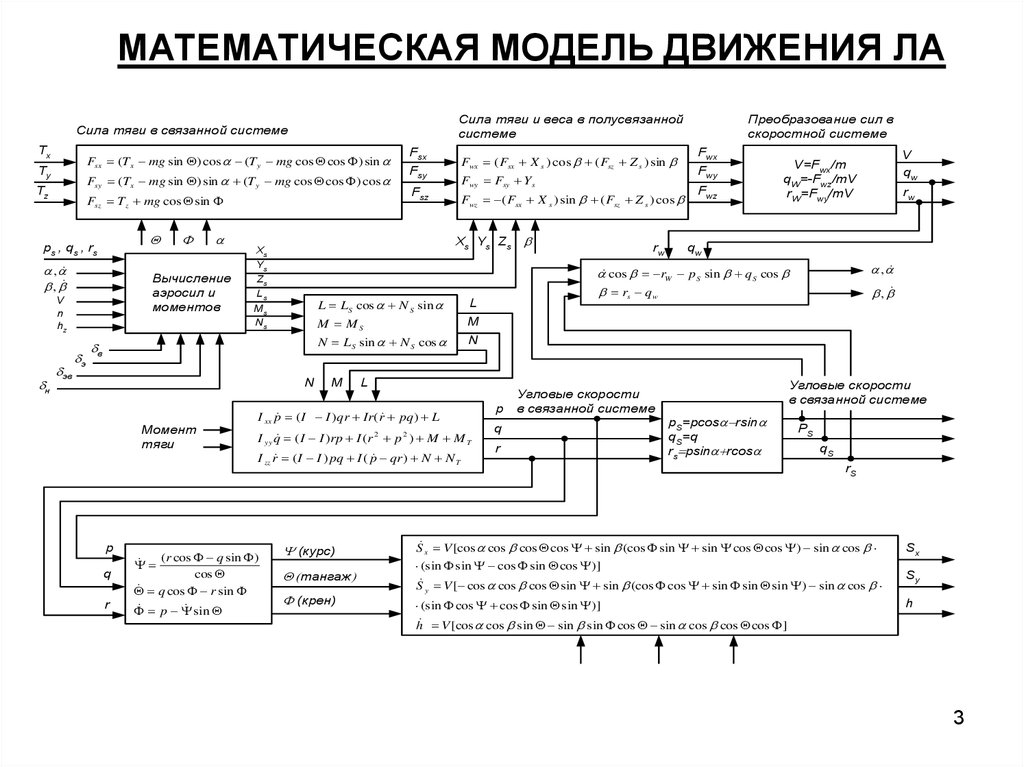
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ ЛА
Сила тяги и веса в полусвязанной
системе
Сила тяги в связанной системе
Tx
Fsx (Tx mg sin ) cos (T y mg cos cos ) sin
Ty
Fsy (Tx mg sin ) sin (T y mg cos cos ) cos
Tz
Fsz Tz mg cos sin
ps , q s , r s
,
,
эв
Вычисление
аэросил и
моментов
V
n
hz
н
э
N
p
q
r
Fwx ( Fsx X s ) cos ( Fsz Z s ) sin
Fsy
Fwy Fsy Ys
Fsz
Fwz ( Fsx X s ) sin ( Fsz Z s ) cos
Xs Ys Zs
Xs
Ys
Zs
Ls
Ms
Ns
в
Момент
тяги
Fsx
L LS cos N S sin
L
M MS
M
N L S sin N S cos
N
M
I yy q ( I I )rp I (r 2 p 2 ) M M T
I zz r ( I I ) pq I ( p qr ) N N T
(r cos q sin )
cos
q cos r sin
sin
p
(курс)
тангаж
(крен)
rw
Fwx
Fwy
Fwz
p
q
r
Угловые скорости
в связанной системе
V
qw
V=Fwx/m
qW=-Fwz/mV
rW=Fwy/mV
rw
qw
,
cos rW p S sin q S cos
rs q w
L
I xx p ( I I )qr Ir (r pq) L
Преобразование сил в
скоростной системе
,
Угловые скорости
в связанной системе
pS=pcos rsin
qS=q
rs psin rcos
PS
qS
rS
S x V [cos cos cos cos sin (cos sin sin cos cos ) sin cos
Sx
(sin sin cos sin cos )]
S y V [ cos cos cos sin sin (cos cos sin sin sin ) sin cos
Sy
(sin cos cos sin sin )]
h V [cos cos sin sin sin cos sin cos cos cos ]
h
3

4.

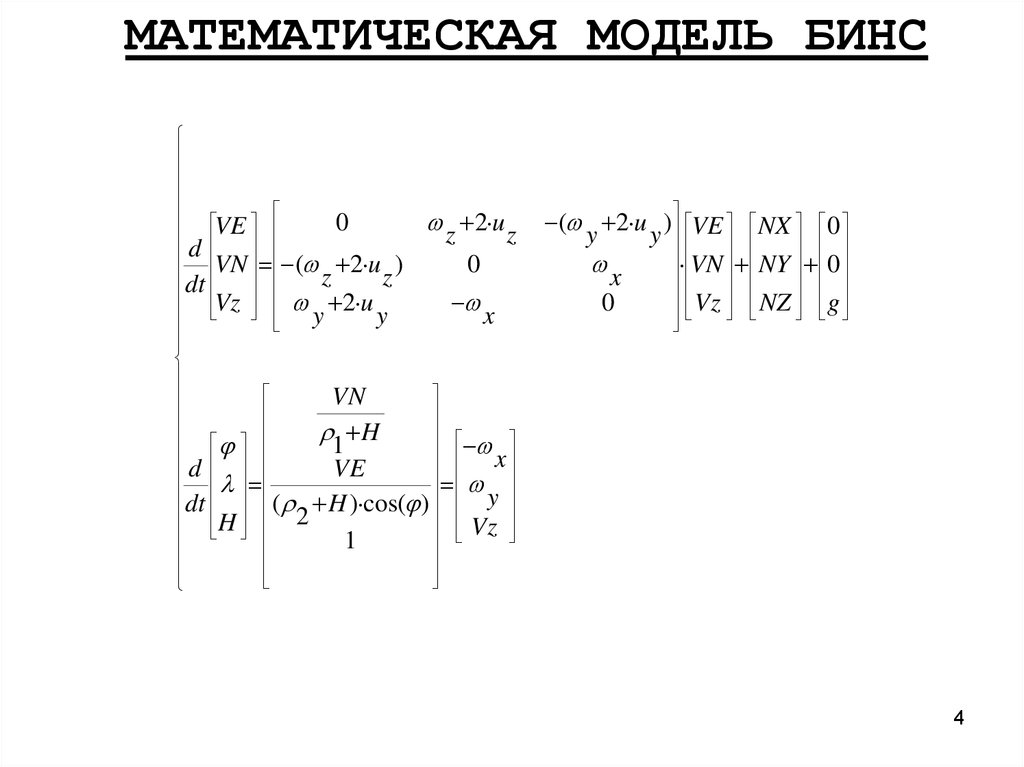
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ БИНС
VE
0
z 2 u z
d
0
VN ( z 2 u z )
dt
Vz 2 u
y
y
x
VN
1 H
x
VE
d
y
dt
(
H
)
cos(
)
2
H
Vz
1
( 2 u ) VE NX 0
y
y
x
VN
NY
0
g
0
Vz
NZ
4

5.

Уравнения Пуассона
0
d Cij
z
dt
y
z
0
x
x x
y y uy
z z uz
y
x Cij Cij
0
0
3
2
NX
NY C
ij
NZ
3
0
1
2
1
0
n1
n2
n3
5

6.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ БИНС
u y u cos( )
a (1 e 2 )
1
(1 e 2 sin 2 ( ))3 / 2
u z u sin( )
u 7292115 10
a
2
(1 e 2 sin 2 ( ))1 / 2
11
рад. / с.
а = 6378245 м – экваториальный
полудиаметр (эллипсоид Красовского
ПЗ42);
e2 = 0.0066934126 – эксцентриситет.
x
y cos( )
y sin( )
6

7.

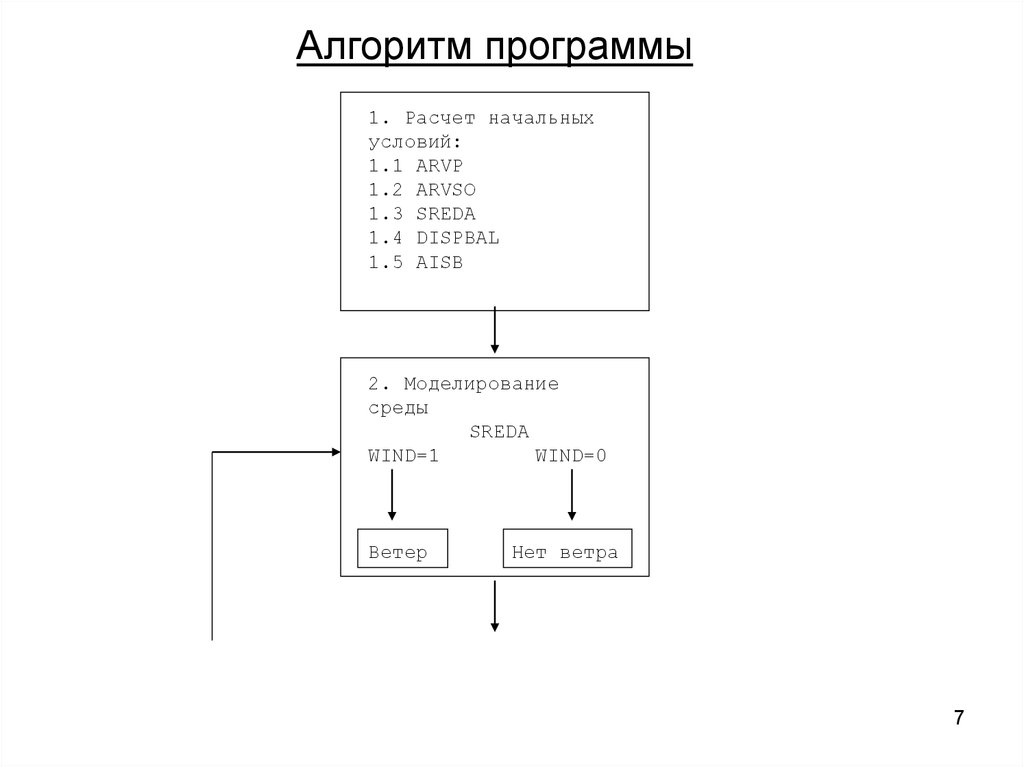
Алгоритм программы
1. Расчет начальных
условий:
1.1 ARVP
1.2 ARVSO
1.3 SREDA
1.4 DISPBAL
1.5 AISB
2. Моделирование
среды
SREDA
WIND=1
WIND=0
Ветер
Нет ветра
7

8.

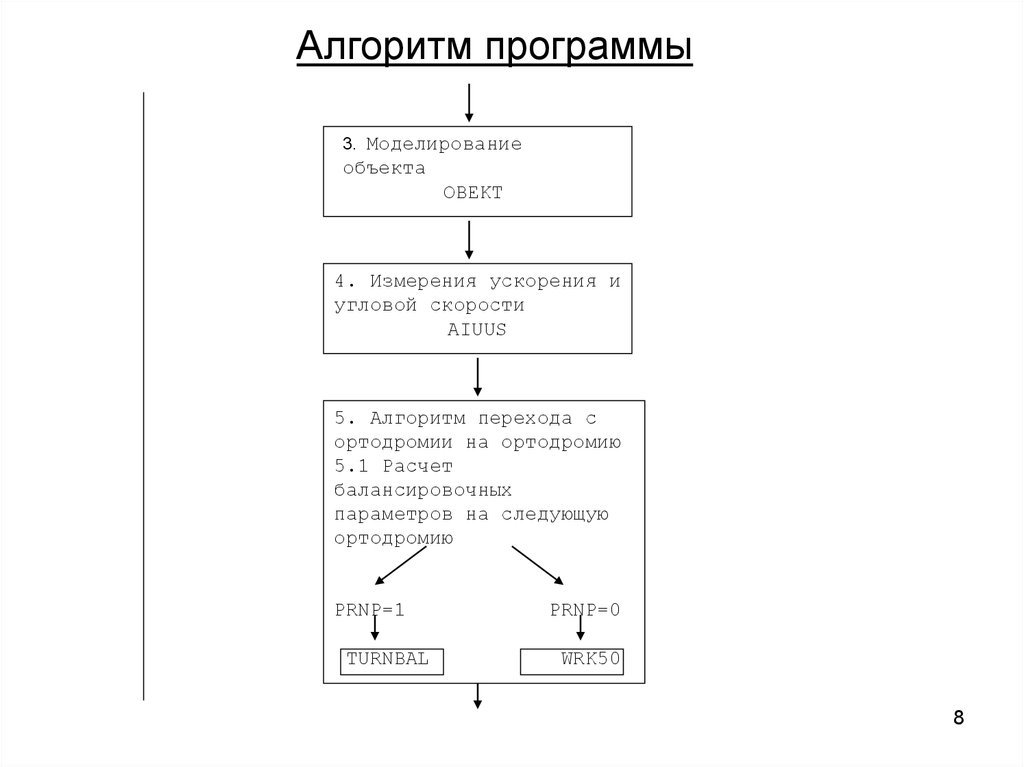
Алгоритм программы
3. Моделирование
объекта
OBEKT
4. Измерения ускорения и
угловой скорости
AIUUS
5. Алгоритм перехода с
ортодромии на ортодромию
5.1 Расчет
балансировочных
параметров на следующую
ортодромию
PRNP=1
TURNBAL
PRNP=0
WRK50
8

9.

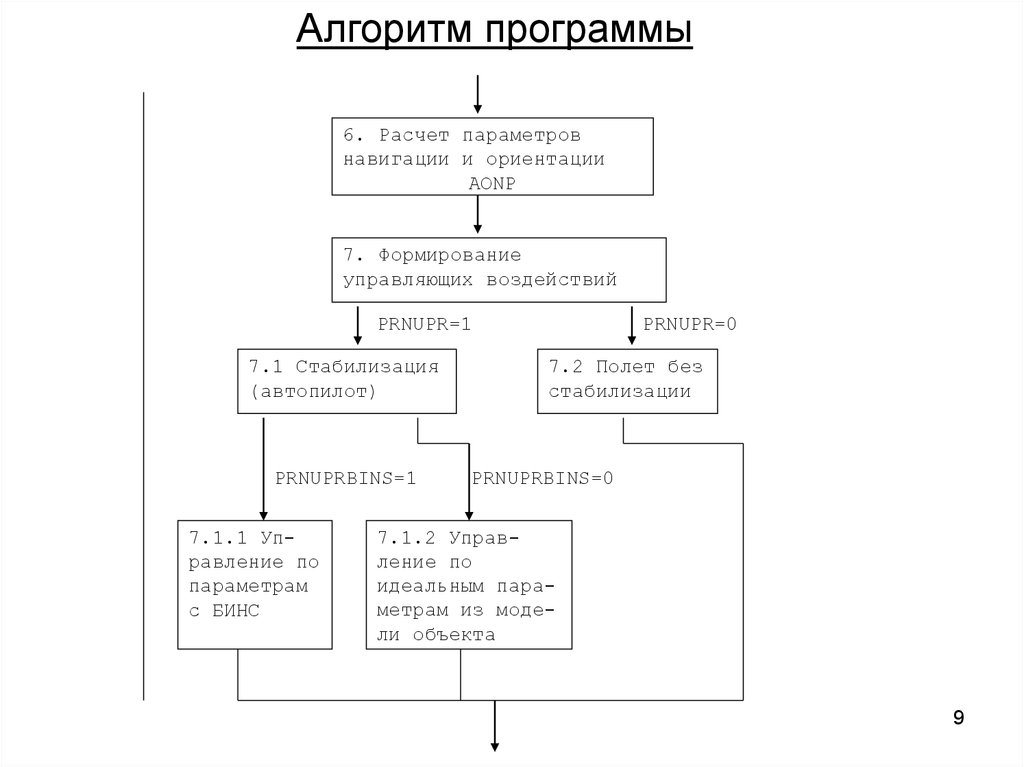
Алгоритм программы
6. Расчет параметров
навигации и ориентации
AONP
7. Формирование
управляющих воздействий
PRNUPR=1
7.1 Стабилизация
(автопилот)
PRNUPRBINS=1
7.1.1 Управление по
параметрам
с БИНС
PRNUPR=0
7.2 Полет без
стабилизации
PRNUPRBINS=0
7.1.2 Управление по
идеальным параметрам из модели объекта
9

10.

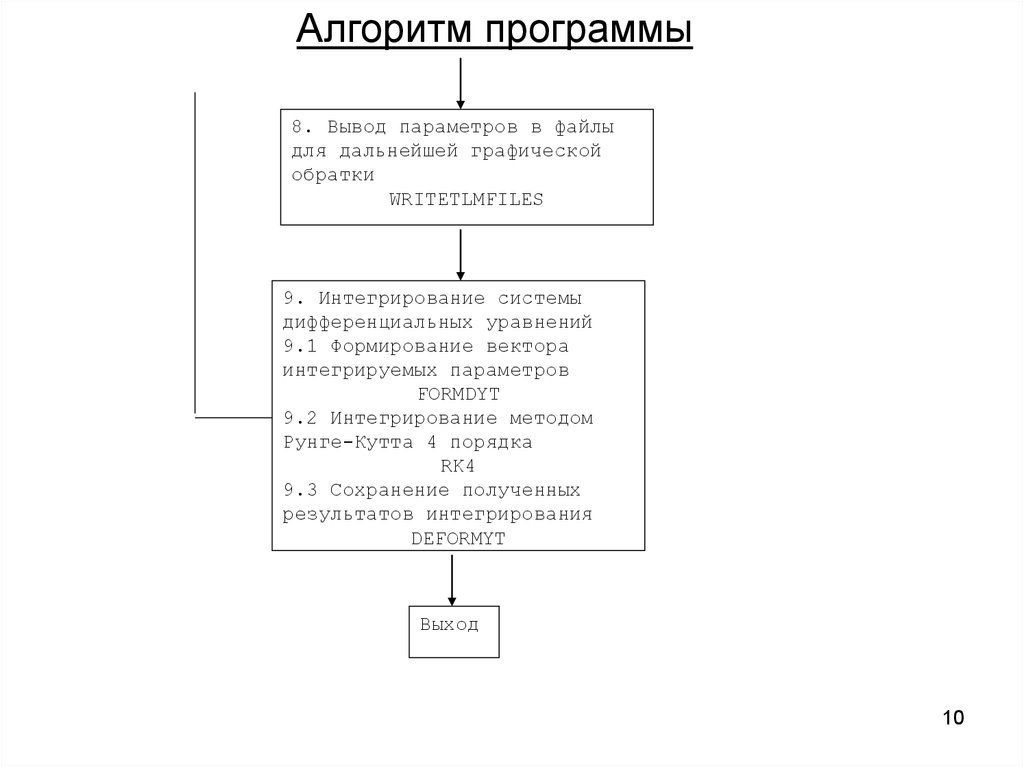
Алгоритм программы
8. Вывод параметров в файлы
для дальнейшей графической
обратки
WRITETLMFILES
9. Интегрирование системы
дифференциальных уравнений
9.1 Формирование вектора
интегрируемых параметров
FORMDYT
9.2 Интегрирование методом
Рунге-Кутта 4 порядка
RK4
9.3 Сохранение полученных
результатов интегрирования
DEFORMYT
Выход
10

11.

МОДЕЛЬ ОШИБОК БИНС
BxП Wax kax f x U az f y U ay f z x (n)
ByП Way U az f x kay f y U ax f z y (n)
BzП Waz U ay f x U ax f y kaz f z z (n),
xП О Дx k Дx X U Дz Y U Дy Z x (n)
yП О Дy U Дz X k Дy Y U Дx Z y (n)
zП О Дz U Дy X U Дx Y k Дz Z z (n)
11

12.

МОДЕЛЬ ОШИБОК БИНС
i (n) C Ai Ai (n) d Ai i (n 1)
где i x, y, z
C Ai Ai 1 Ai2 0, 003 м / с 2
d Ai Ai e
2 f Ai t Ai
0, 00000015
i (n) Ci Бi (n) di i (n 1)
где i x, y, z
Ci Бi 1 Бi2 0, 00057 град/с 0,00001 1/с
di Бi e
2 f Бi t Бi
0, 00187
12

13.

МОДЕЛЬ ОШИБОК БИНС
axП f X BxП
a y П fY B y П
azП f Z BzП
xП X xП
yП Y yП
zП Z z П
Оси
О1X1
О1Y1
О1Z1
О1XП
1
Z
- Y
О1YП
- Z
1
X
О1ZП
Y
- X
1
f X a X1 Z a Y1 Y a Z1
fY aY1 Z a X1 X a Z1
f Z aZ1 Y a X1 X a Y1
X X1 Z Y1 Y Z1
Y Y1 Z X1 X Z1
Z Z1 Y X1 X Y1
13

14.

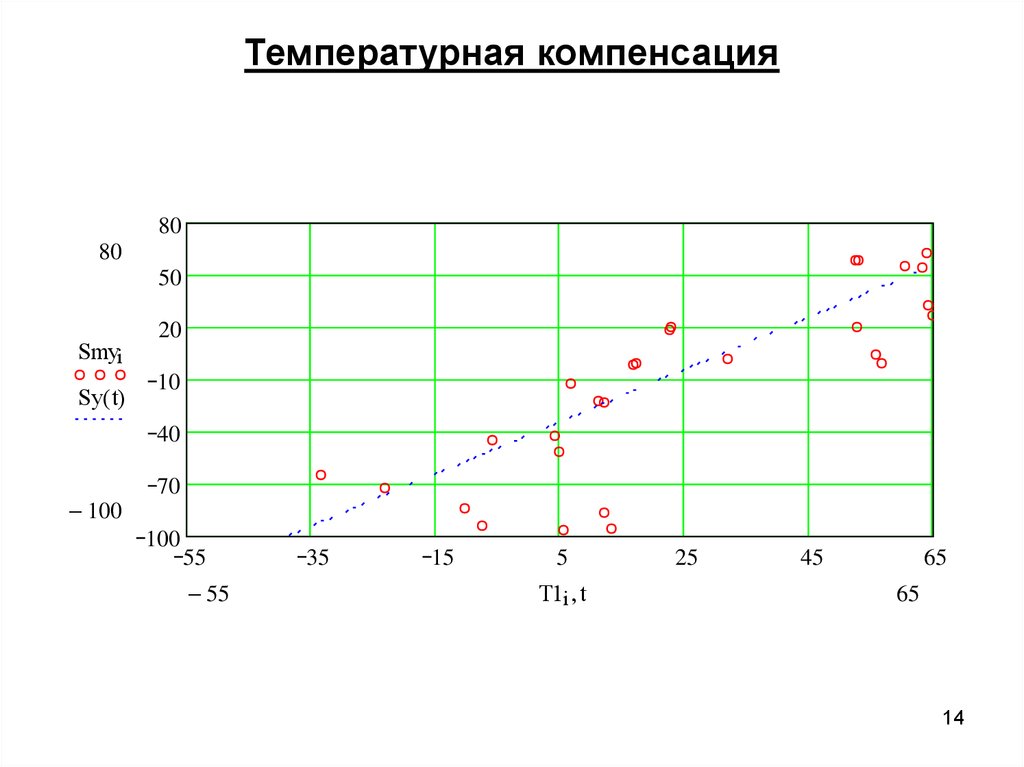
Температурная компенсация
80
80
50
20
Smyi
10
Sy( t)
40
70
100
100
55
55
35
15
5
T1i t
25
45
65
65
300
200
14

15.

Результаты моделирования
Сравним результаты моделирования:
1) Движение объекта с возмущенной
средой (с ветром), управление по
данным с БИНС. БИНС с ошибками
(без температурной компенсации)
NENOL1POST=0.014649
NENOL2POST=0.024414
NENOL3POST=0.012878
SIGMANENOL1=0.00473
SIGMANENOL2=0.00839
SIGMANENOL3=0.003967
MONENOL1=0.00049
MONENOL2=0.00049
MONENOL3=0.00049
NENOL1POSTGIR=0.000000024
NENOL2POSTGIR=0.000000027
NENOL3POSTGIR=0.000000005
SIGMANENOLGIR1=0.000000008
SIGMANENOLGIR2=0.000000002
SIGMANENOLGIR3=0.000000007
MONENOL1GIR=0.000072717
MONENOL2GIR=0.000072717
MONENOL3GIR=0.000072717
1) Движение объекта с возмущенной
средой (с ветром), управление по
данным с БИНС. БИНС с ошибками
(с температурной компенсации)
NENOL1POST=0.0
NENOL2POST=0.0
NENOL3POST=0.0
SIGMANENOL1=0.00183
SIGMANENOL2=0.00153
SIGMANENOL3=0.00102
MONENOL1=0.00049
MONENOL2=0.00049
MONENOL3=0.00049
NENOL1POSTGIR=0.0
NENOL2POSTGIR=0.0
NENOL3POSTGIR=0.0
SIGMANENOLGIR1=0.000000002
SIGMANENOLGIR2=0.00000000049
SIGMANENOLGIR3=0.00000000099
MONENOL1GIR=0.000072717
MONENOL2GIR=0.000072717
MONENOL3GIR=0.000072717
15

16.

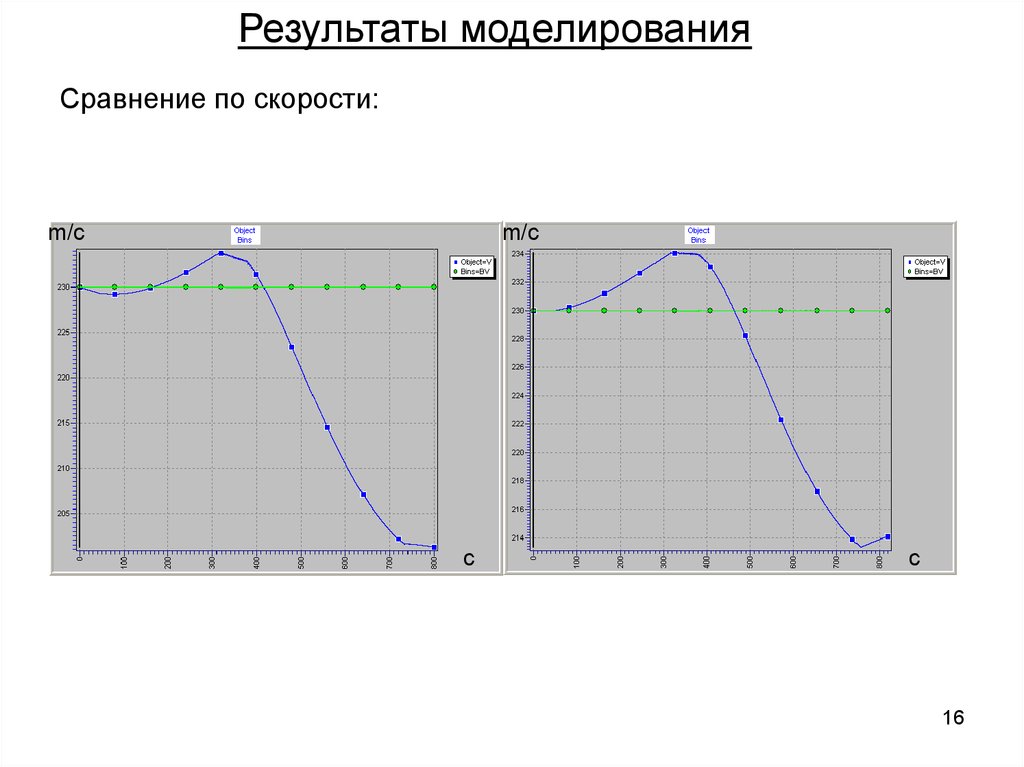
Результаты моделирования
Сравнение по скорости:
m/c
m/c
c
c
16

17.

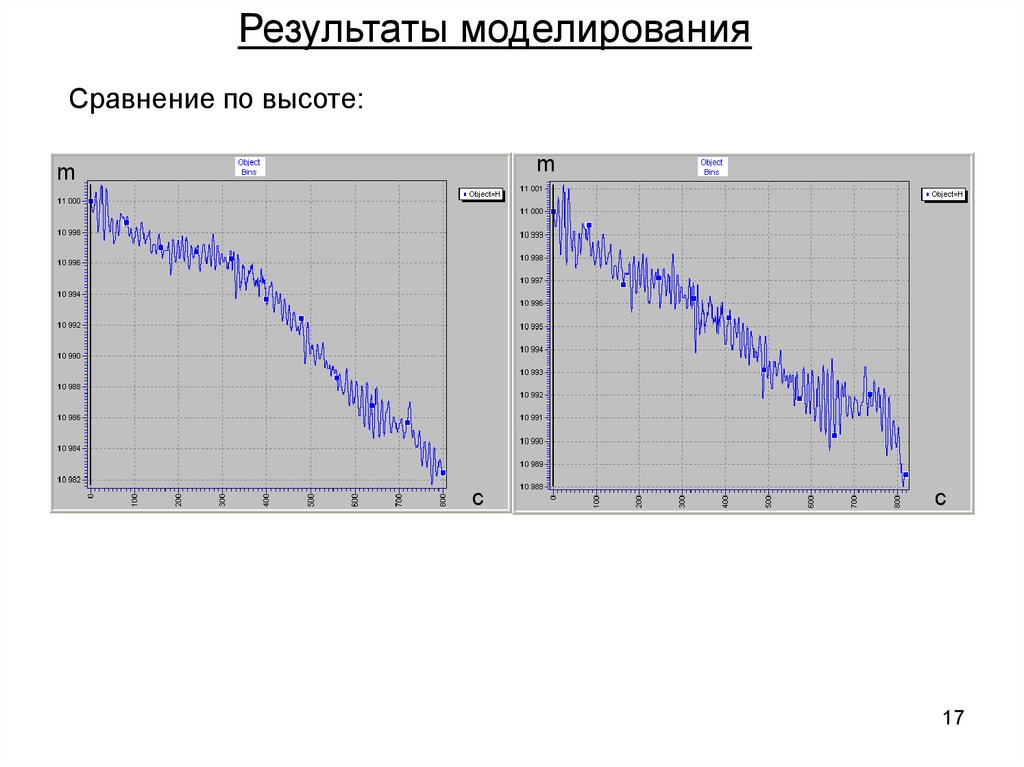
Результаты моделирования
Сравнение по высоте:
m
m
c
c
17

18.

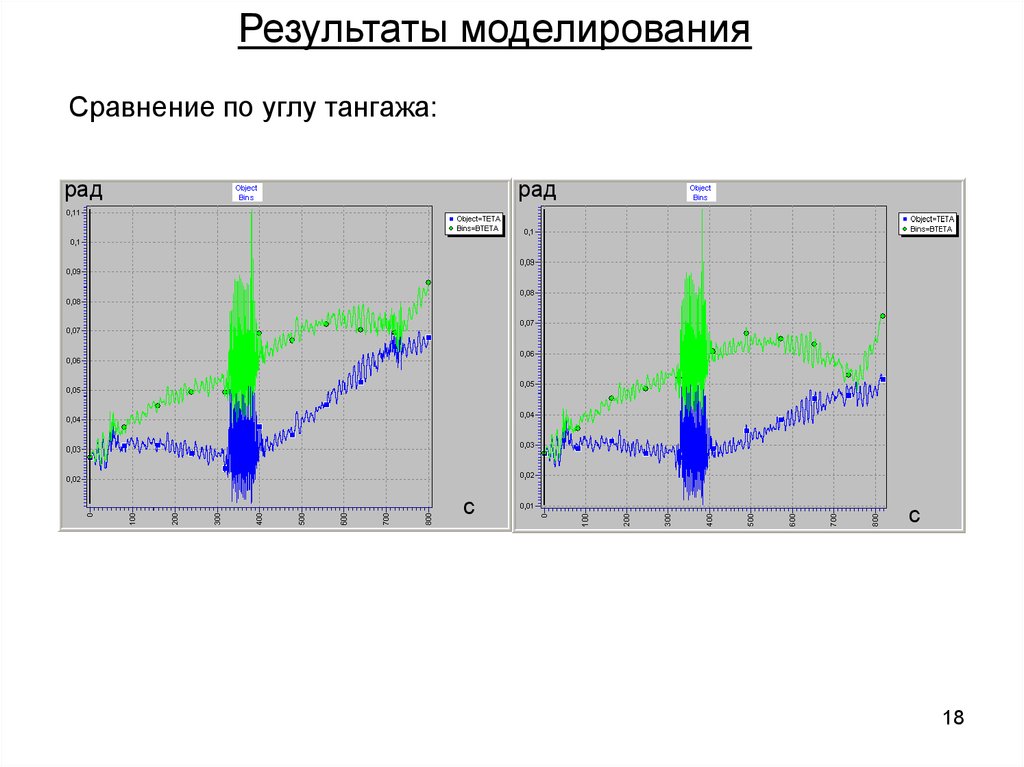
Результаты моделирования
Сравнение по углу тангажа:
рад
рад
c
c
18

19.

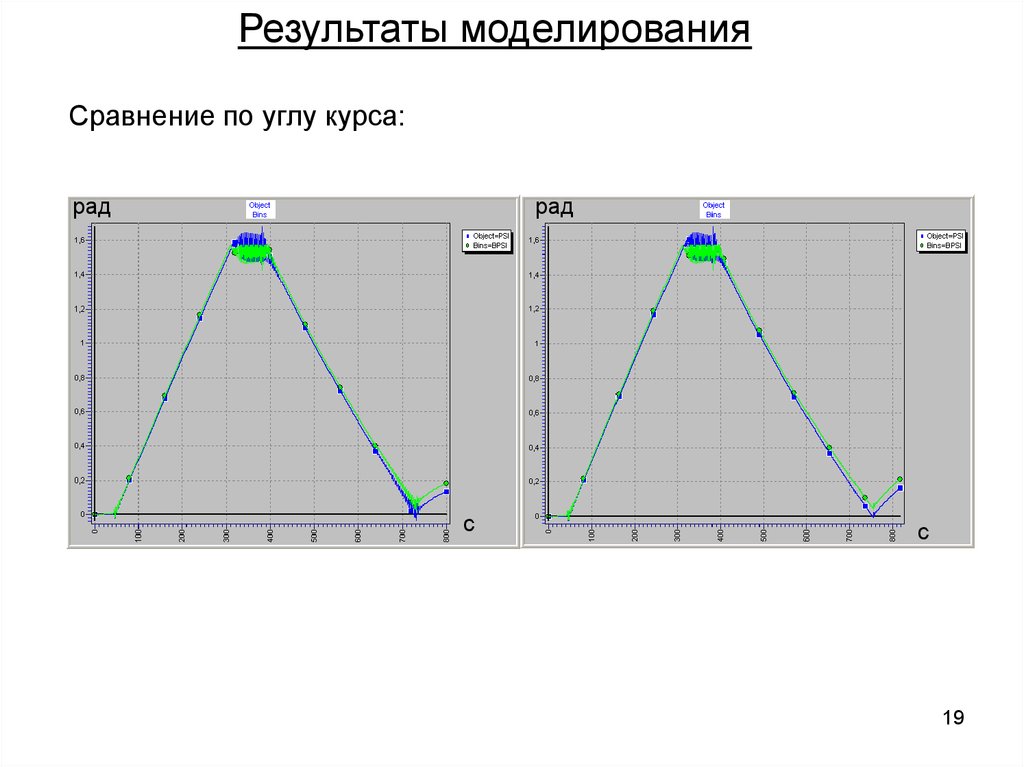
Результаты моделирования
Сравнение по углу курса:
рад
рад
c
c
19

20.

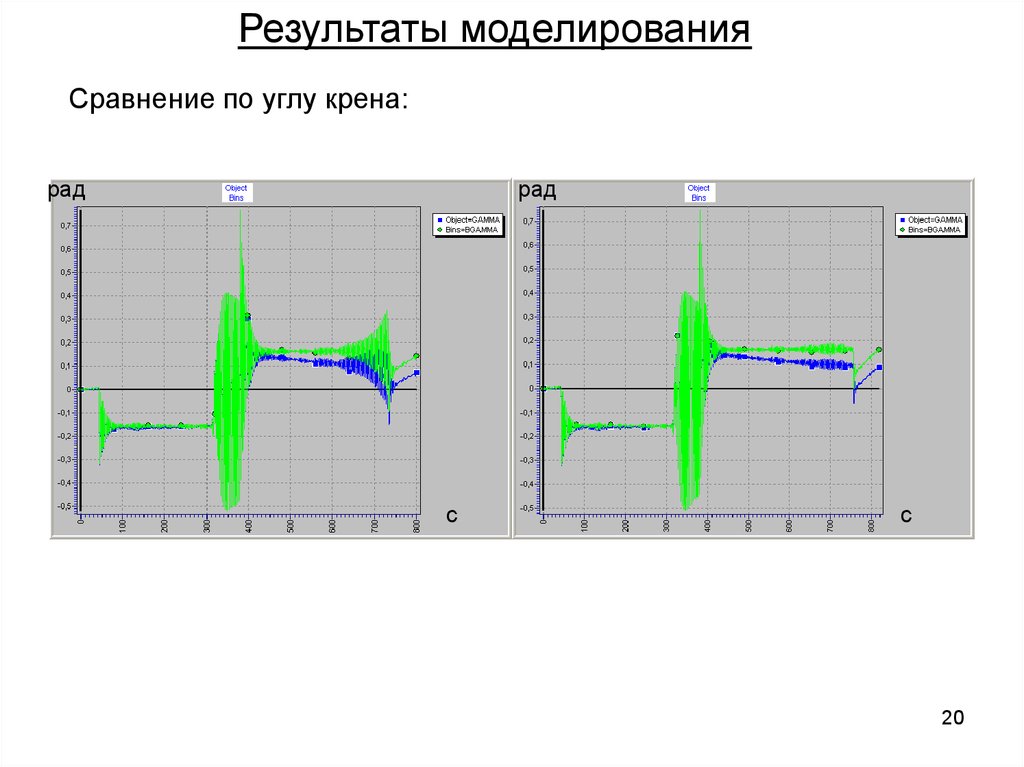
Результаты моделирования
Сравнение по углу крена:
рад
рад
c
c
20

21.

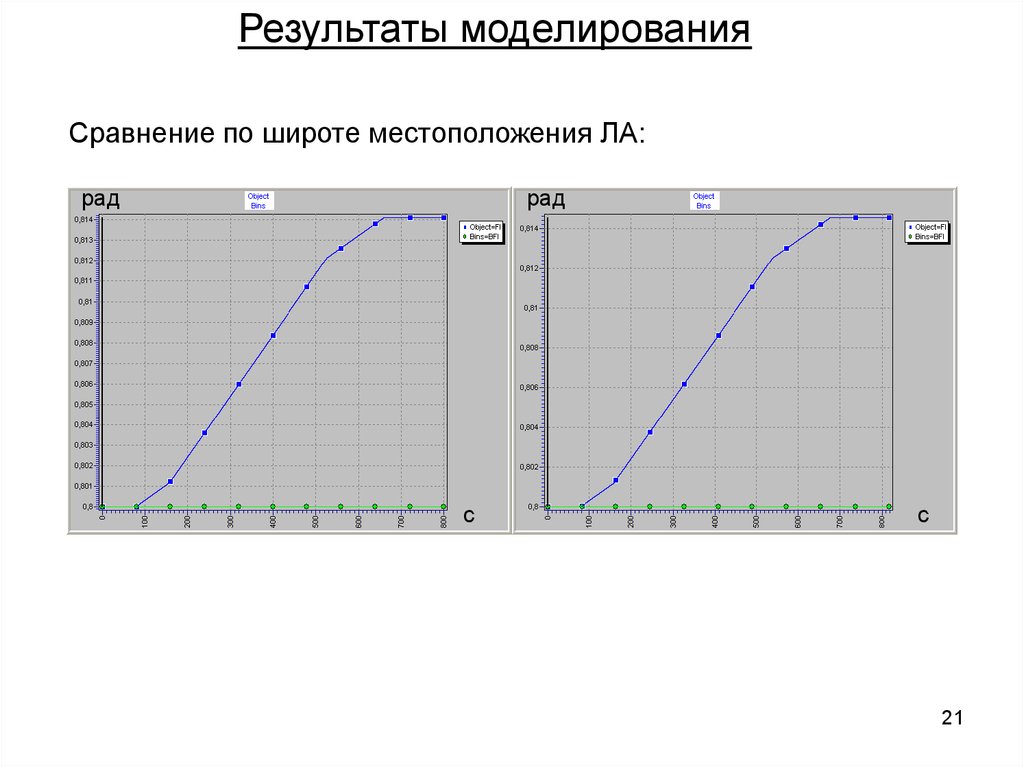
Результаты моделирования
Сравнение по широте местоположения ЛА:
рад
рад
c
c
21

22.

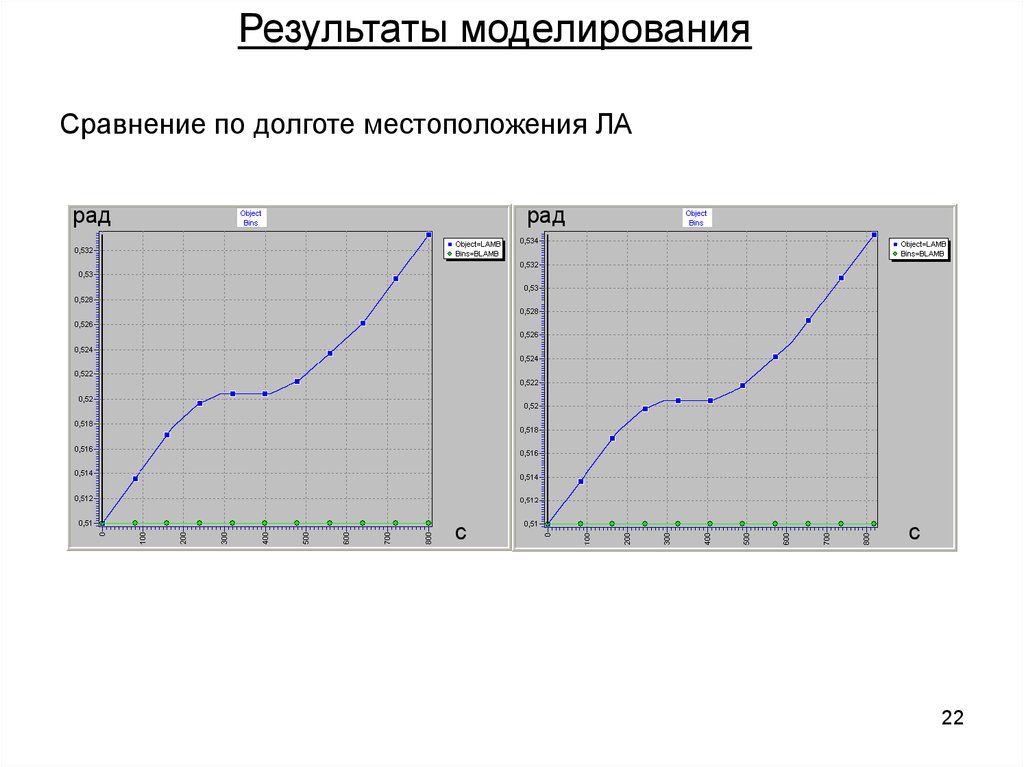
Результаты моделирования
Сравнение по долготе местоположения ЛА
рад
рад
c
c
22