Similar presentations:
Перпендикулярность прямой и плоскости
1.
УРОК №232. 1. Перпендикулярные прямые в пространстве
Ученик должен знать определениеперпендикулярных прямых в пространстве.
Ученик должен знать лемму о
перпендикулярности двух параллельных
прямых третьей прямой
3.
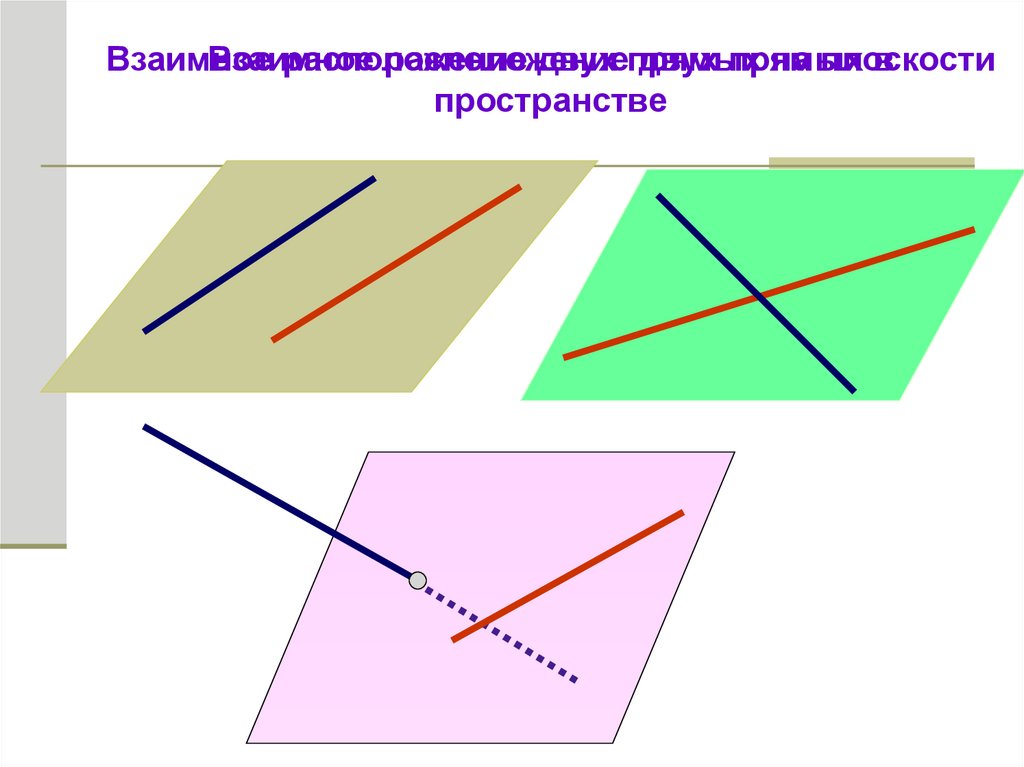
ВзаимноеВзаимное
расположение
расположение
двух прямых
двух прямых
на плоскости
в
пространстве
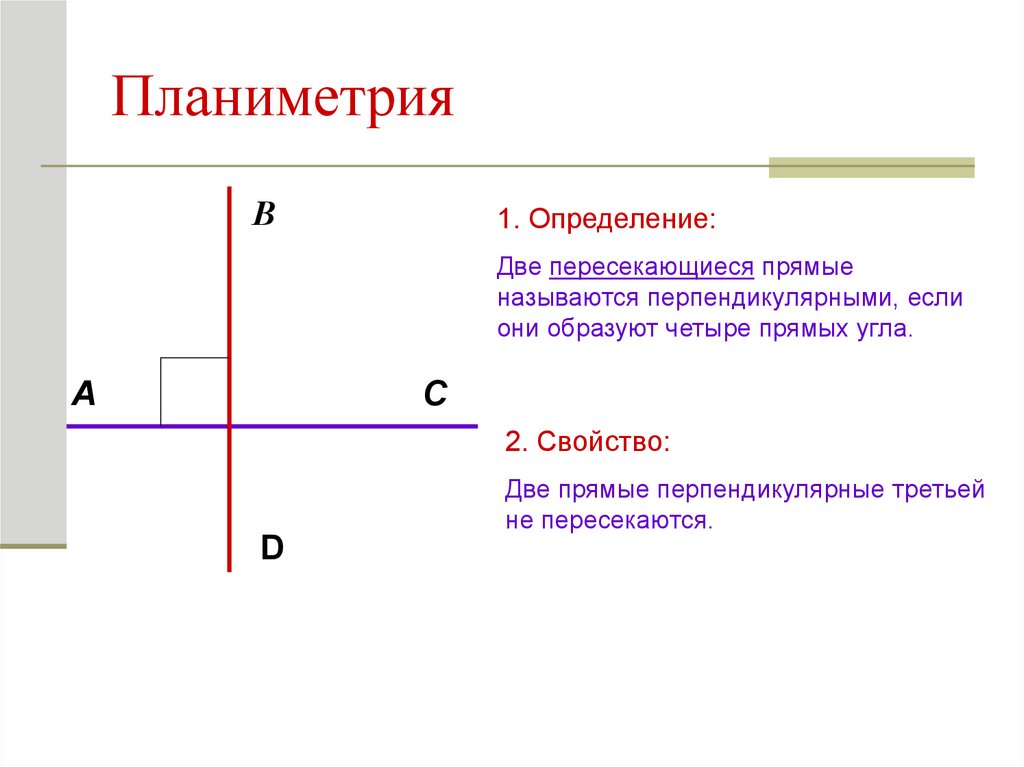
4. Планиметрия
В1. Определение:
Две пересекающиеся прямые
называются перпендикулярными, если
они образуют четыре прямых угла.
С
A
2. Свойство:
Две прямые перпендикулярные третьей
не пересекаются.
D
5. Стереометрия
ВВ
С
A
С
A
D
D
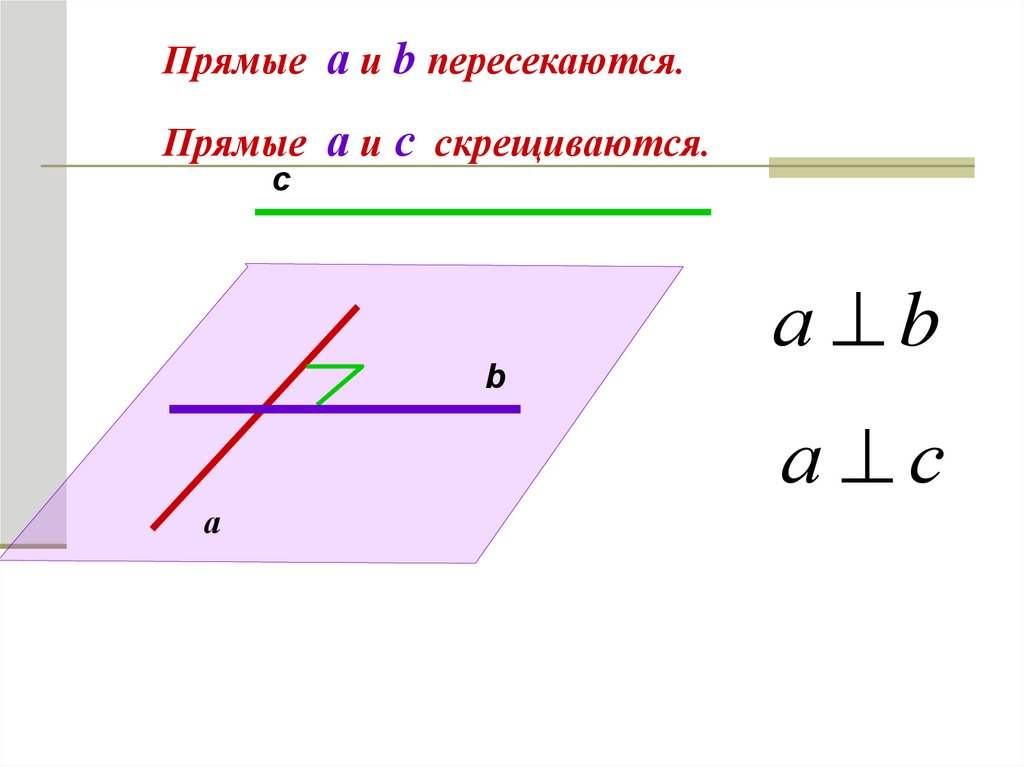
Две прямые в пространстве называются перпендикулярными,
если угол между ними равен 90°.
Взаимное расположение прямых в пространстве
6.
Прямые а и b пересекаются.Прямые а и с скрещиваются.
c
а b
b
а с
а
7.
Лемма о перпендикулярности двухпараллельных прямых к третьей
прямой
а
Дано: а с а b
Если одна из bдвух параллельных
прямых
Доказать b с
перпендикулярна к третьей
прямой,
то
и
Доказательство
другая М
прямая перпендикулярна
к этой
А
c
М а; b; с МА а
прямой
МС с
т.к. а с, то АМС 90
(углы с сонаправленными сторонами)
С
а b МА а то МА b
МА b и МС с; АМС 90
(углы с сонаправленными
сторонами)
то bc 90 , т.е. b c
8. Лемма о перпендикулярности двух параллельных прямых к третьей прямой
2. Параллельные прямые,перпендикулярные к
плоскости.
Знать определение прямой перпендикулярной к
плоскости.
Уметь формулировать и доказывать теоремы
прямую и обратную о параллельных прямых.
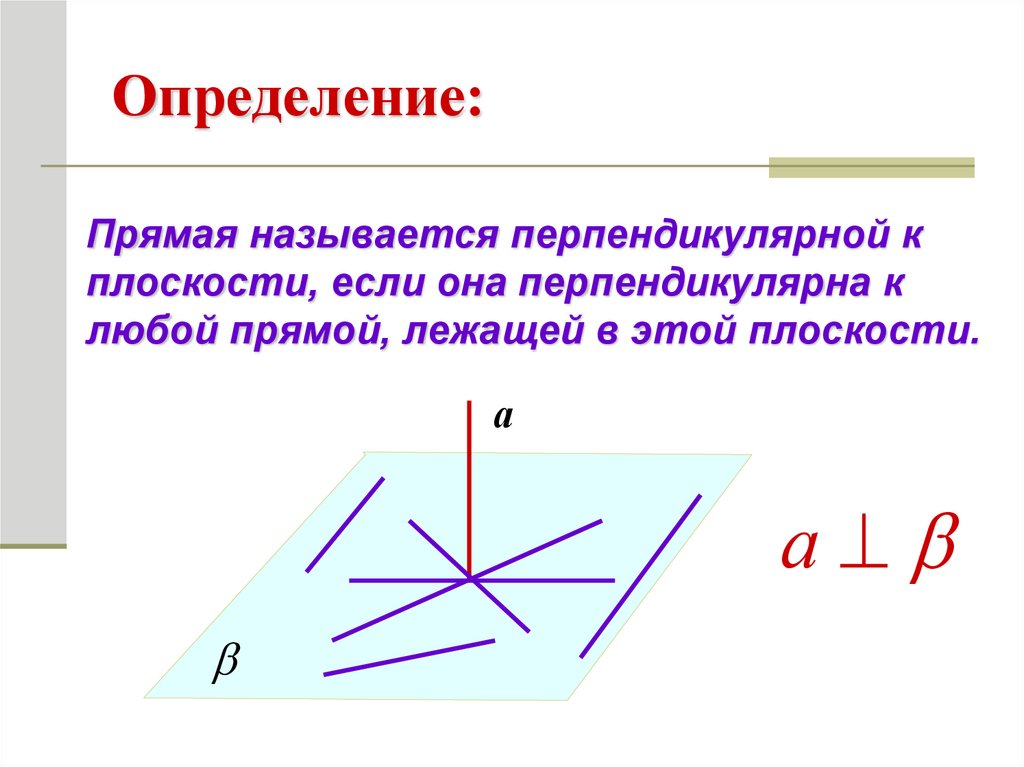
9. 2. Параллельные прямые, перпендикулярные к плоскости.
Определение:Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к
любой прямой, лежащей в этой плоскости.
а
а
10. Определение:
Теорема 1Если одна из двух параллельных прямых
перпендикулярна к плоскости, то другая
прямая перпендикулярна к этой плоскости
Дано: а b а
b
Доказать
а
b
Доказательство
x
а , то а x
x
по лемме b x
b
11. Теорема 1
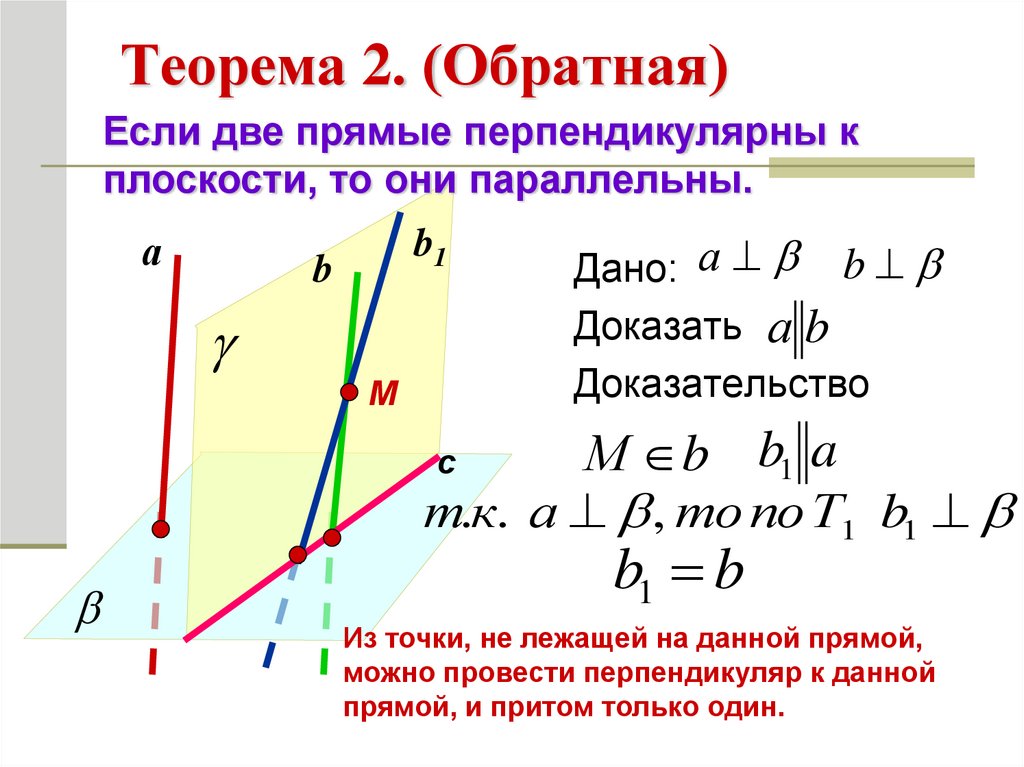
Теорема 2. (Обратная)Если две прямые перпендикулярны к
плоскости, то они параллельны.
а
b1
b
М
Дано: а b
Доказать а b
Доказательство
М b b1 a
т.к. а , то по Т1 b1
с
b1 b
Из точки, не лежащей на данной прямой,
можно провести перпендикуляр к данной
прямой, и притом только один.
12. Теорема 2. (Обратная)
ОДве прямые в пространстве называютсяперпендикулярными, если угол между ними равен
90°.
Л
Если одна из двух параллельных прямых
перпендикулярна к третьей прямой, то и другая
прямая перпендикулярна к этой прямой
О
Прямая называется перпендикулярной к плоскости,
если она перпендикулярна к любой прямой, лежащей
в этой плоскости.
Т1
Если одна из двух параллельных прямых
перпендикулярна к плоскости, то другая прямая
перпендикулярна к этой плоскости
Т2
Если две прямые перпендикулярны к плоскости, то
они параллельны.
13.
Домашнее заданиеп. 15, 16 стр. 34 -36 (знать определения;
формулировки и доказательства
леммы и теорем).
Вопросы № 1, 2, 3, 4 стр. 54
№ 116(б), №117








 mathematics
mathematics








