Объем тел

1.

МКОУ «Погорельская СОШ»

2.

3.

Цели :
• Сформировать навыки нахождения
объема конуса.
• Развитие логического мышления,
пространственного воображения,
умений действовать по алгоритму,
составлять алгоритмы действий.
• Воспитание познавательной
активности, самостоятельности.

4.

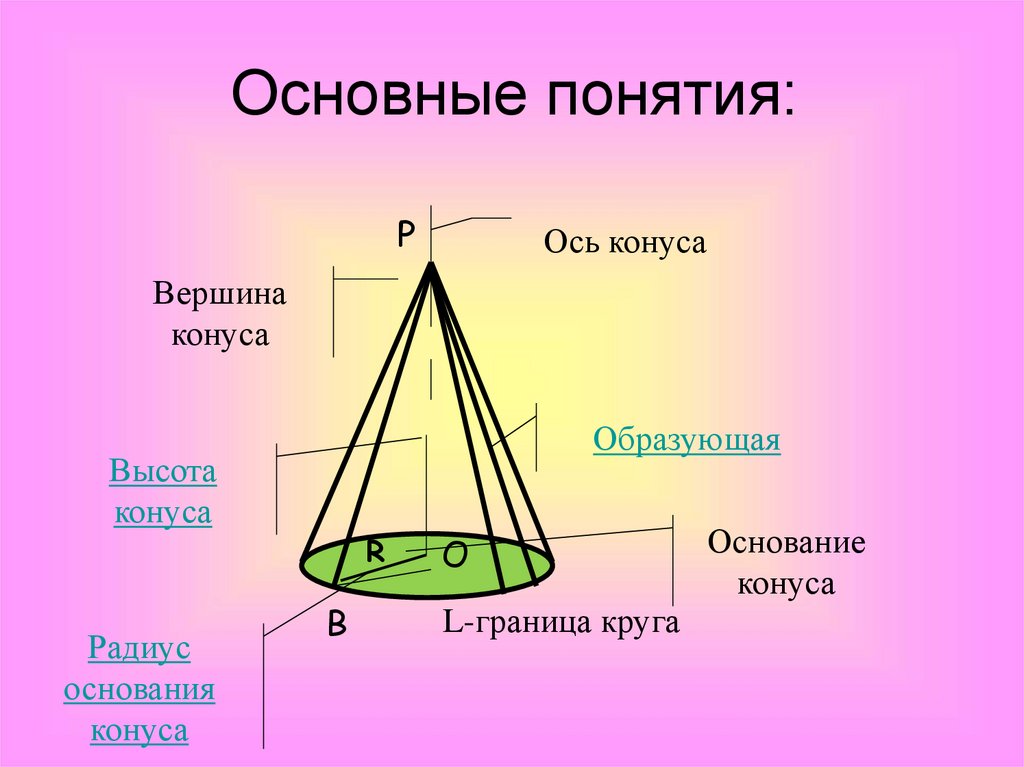
Основные понятия:
P
Ось конуса
Вершина
конуса
Образующая
Высота
конуса
R
Радиус
основания
конуса
B
O
L-граница круга
Основание
конуса

5.

Какая фигура получается в сечении конуса
плоскостью, проходящей через ось конуса?
Равнобедренный треугольник
Какая фигура получается в сечении конуса
плоскостью, проходящей параллельно
плоскости основания?
Круг
Какая фигура получается в сечении конуса
плоскостью, не задевающую плоскость
основания?
Эллипс
Как называется сечение конуса плоскостью
параллельной двум образующим конуса.
Гипербола

6.

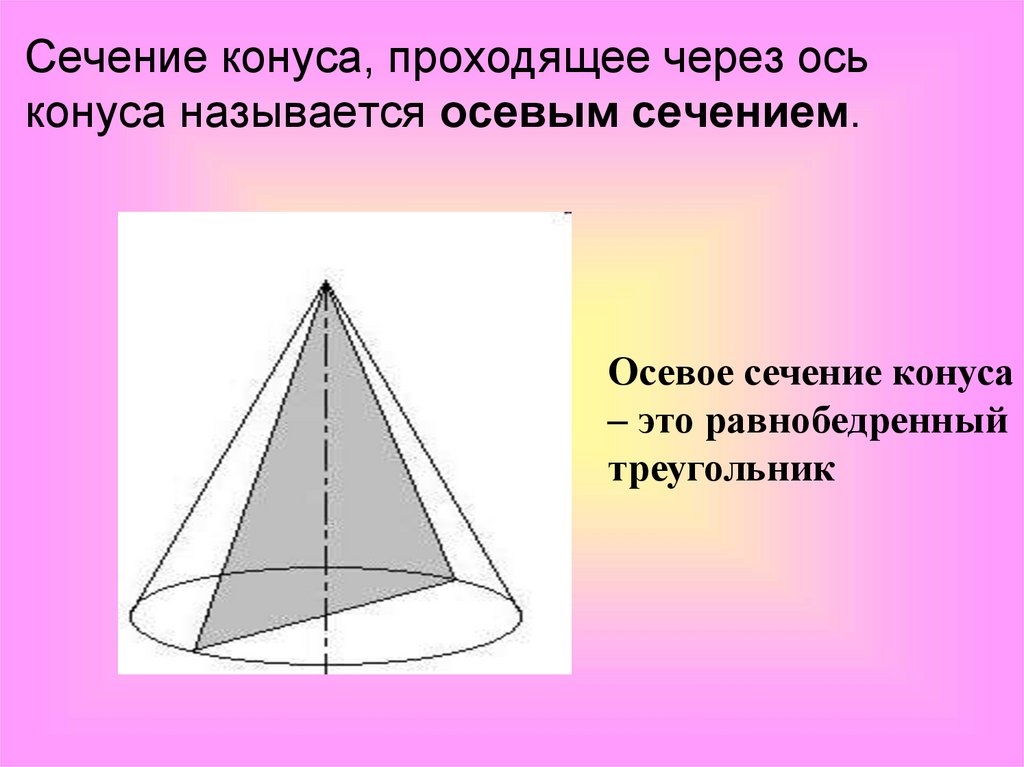
Сечение конуса, проходящее через ось
конуса называется осевым сечением.
Осевое сечение конуса
– это равнобедренный
треугольник

7.

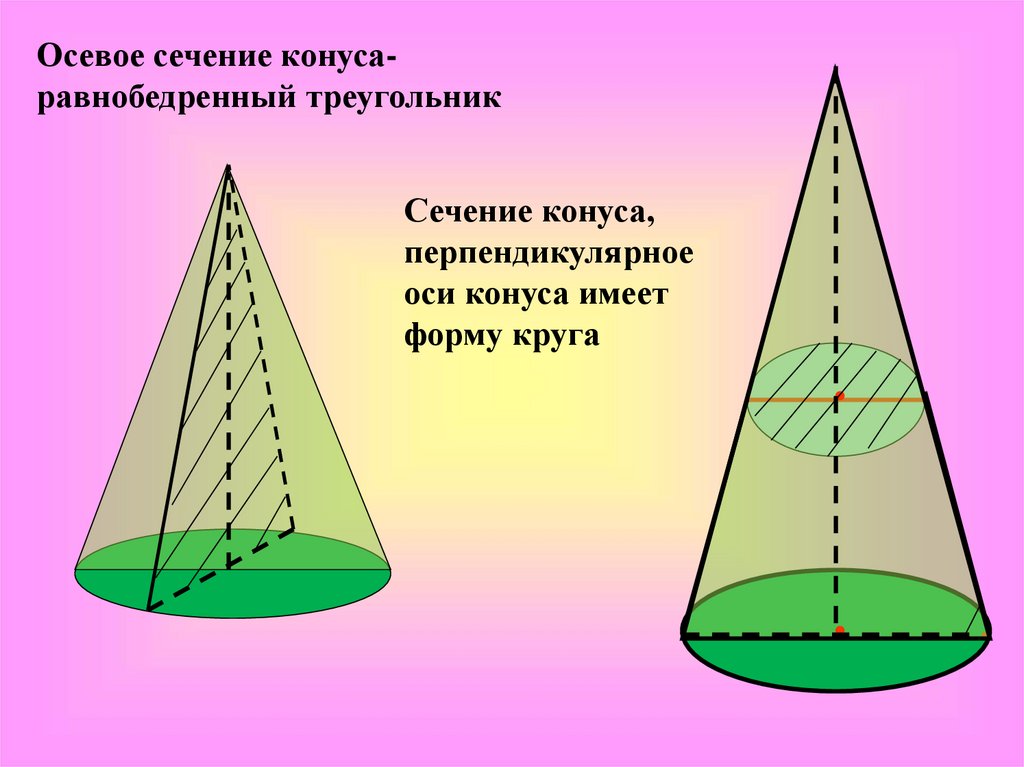
Осевое сечение конусаравнобедренный треугольник
Сечение конуса,
перпендикулярное
оси конуса имеет
форму круга

8.

Сечение плоскостью, пересекающей все образующие
конуса, - эллипс. (не задевает плоскость основания)
Сечение плоскостью, параллельной двум
образующим конуса, - гипербола.
Сечение плоскостью, параллельной одной
образующей конуса, - парабола.

9.

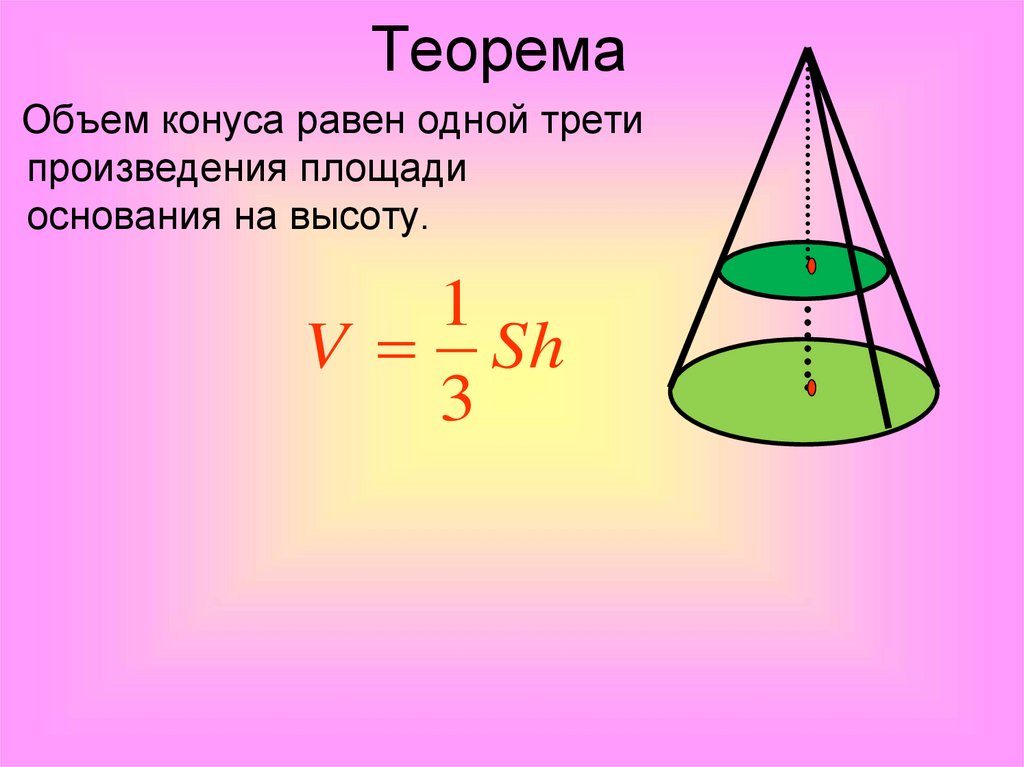
Теорема
Объем конуса равен одной трети
произведения площади
основания на высоту.
1
V Sh
3

10.

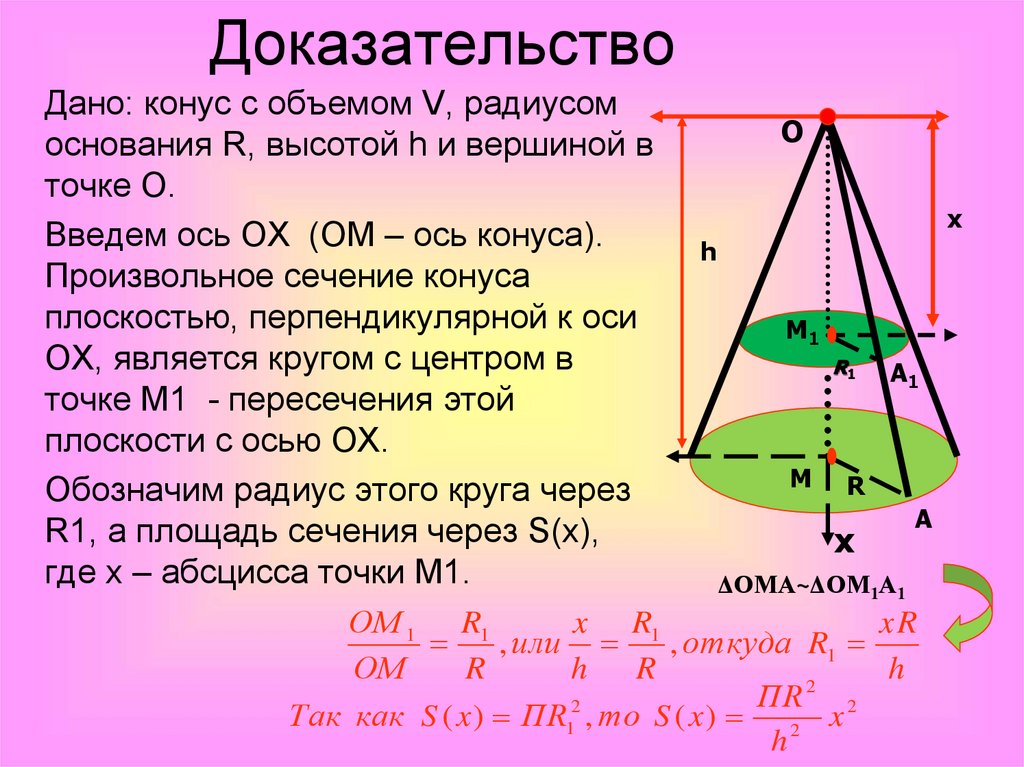
Доказательство
Дано: конус с объемом V, радиусом
основания R, высотой h и вершиной в
точке О.
Введем ось ОХ (ОМ – ось конуса).
Произвольное сечение конуса
плоскостью, перпендикулярной к оси
ОХ, является кругом с центром в
точке М1 - пересечения этой
плоскости с осью ОХ.
Обозначим радиус этого круга через
R1, а площадь сечения через S(х),
где х – абсцисса точки М1.
O
х
h
М1
R1
М
A1
R
х
A
ΔОМА~ΔОМ1А1
ОМ 1 R1
x R
xR
, или 1 , откуда R1
ОМ
R
h
R
h
2
ПR 2
Так как S ( x ) ПR12 , то S ( x )
x
2
h

11.

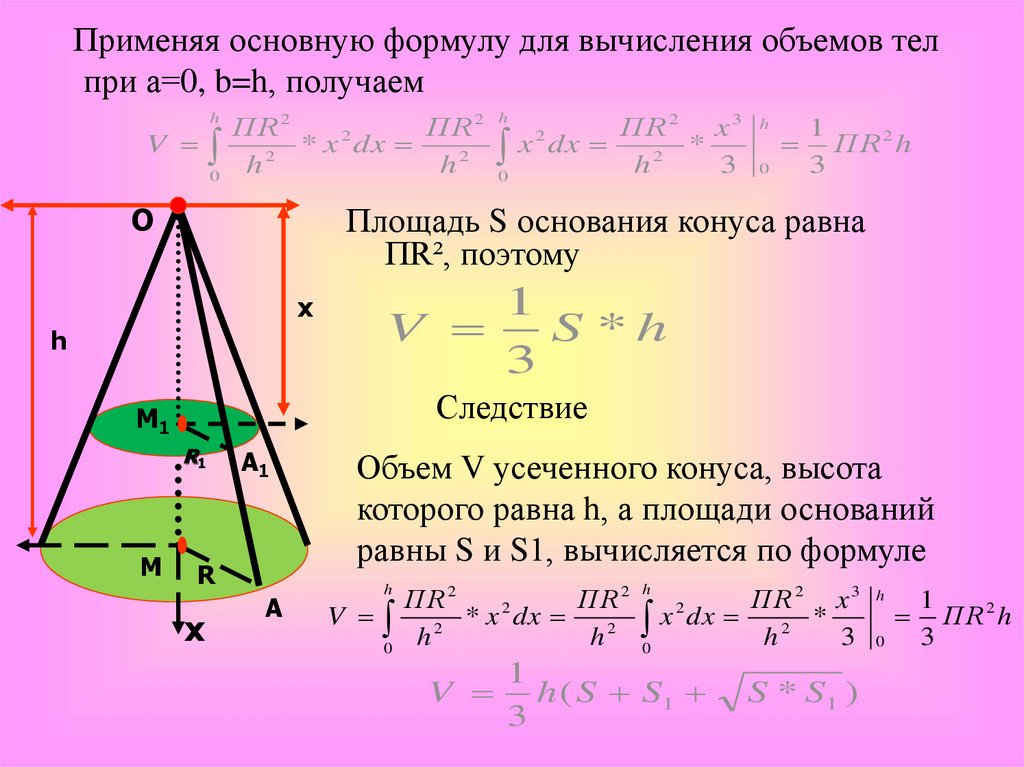
Применяя основную формулу для вычисления объемов тел
при а=0, b=h, получаем
h
V
0
ПR 2
ПR 2
2
* x dx
h2
h2
ПR 2 x 3
0 x dx h 2 * 3
2
h
0
1
ПR 2 h
3
Площадь S основания конуса равна
ПR², поэтому
O
1
V
S *h
3
х
h
Следствие
М1
R1
М
h
A1
R
х
A
Объем V усеченного конуса, высота
которого равна h, а площади оснований
равны S и S1, вычисляется по формуле
h
V
0
ПR 2
ПR 2
2
* x dx
2
h
h2
h
ПR 2 x 3
0 x dx h 2 * 3
2
1
V h ( S S1
3
S * S1 )
h
0
1
ПR 2 h
3

12.

Решение задач с целью закрепления материала
Ответы
1. Вычислить объем конуса , если его высота равна 6см, а площадь основания
42см2 .
2. Объем конуса с радиусом основания 4м и высотой 6м равен ?
3. Найдите площадь основания конуса , если его объем равен 256см3, а
высота 4м.
4. Вычислите объем усеченного конуса , если радиусы его оснований равны
3см, а площадь основания 16см2 и 4см2.
5. Вычислите объем усеченного конуса, если радиусы его оснований равны
3см и 9см, а высота 6см.
Ответы:
1. 84см3 , 2. 32Пм3, 3. 192см2, 4. 32см3 , 5. 234Псм3

13.

Решение задач
Зад. №1. Образующая конуса L составляет с плоскостью основания угол ß.
Найдите объем конуса.
Дано: Конус, треугольник РАВ-осевое сечение конуса,РА=РВ=L, РО-высота.
Найти: Vконуса-?
Решение:
Vкон.= 1/3·Пr2h , V=1/3·П·АО2·РО.
Р
РО/L=sinß, РО=sinß·L,
Из треугольника АРО (<О=900)
АО/L=cosß, АО=cosß·L
V=1/3·П·L·2cos2ß·L·sinß= 1/3·П·L3·2sinßcosß·1/2·cosß =
L
= 1/3·1/2·П·L3·sin2ßcosß=1/6·П·L3·sin2ßcosß
ß
А
О
Ответ:
В
V=1/6·П·L·3·sin2ßcosß

14.

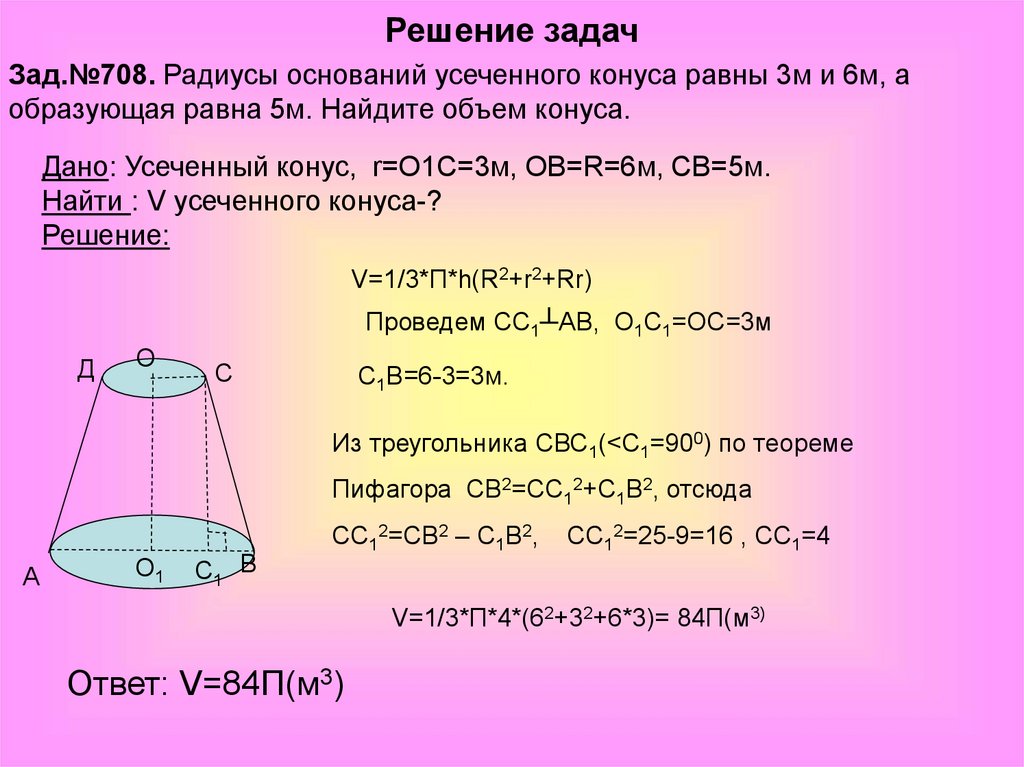
Решение задач
Зад.№708. Радиусы оснований усеченного конуса равны 3м и 6м, а
образующая равна 5м. Найдите объем конуса.
Дано: Усеченный конус, r=О1С=3м, ОВ=R=6м, СВ=5м.
Найти : V усеченного конуса-?
Решение:
V=1/3*П*h(R2+r2+Rr)
Проведем СС1┴АВ, О1С1=ОС=3м
Д
О
С
С1В=6-3=3м.
Из треугольника СВС1(<С1=900) по теореме
Пифагора СВ2=СС12+С1В2, отсюда
А
О1
С1 В
СС12=СВ2 – С1В2,
СС12=25-9=16 , СС1=4
V=1/3*П*4*(62+32+6*3)= 84П(м3)
Ответ: V=84П(м3)

15.

Решение задач
Зад.№2. Образующая конуса равна 60см, высота 30см. Найдите Vкон.
Дано:Конус РАВ , РО – высота, РА=60см, РО=30см.
Найти : V конуса-?
Решение:
V=1/3*Пr2h
Р
Из треугольника АОР (<О=900)
так как РО=АР/2 , то <А=300
60
30
R=АО=60*cos300=60*√3/2=30√3 (см)
А
300
О
В
V=1/3*П*(30√3)2= 27000П(см3)
Ответ: V=27000П(см3)

16.

Решение задач
Зад.№3. Образующая конуса равна 12см, наклонена к плоскости
основания под углом 300. Найдите Vкон.
Дано:Конус SАВ, SА=12см, <SAO=300.
Найти : V конуса-?
Решение:
V=1/3·Пr2h
S
V=1/3·П·АО2·SО .
из треугольника АSО (<О=900), h=SO=1/2·АС=6см.
12
А
R=АО=12·cos300=12·√3/2=6√3(cм)
300
О
В
V=1/3·П·(6√3)2·6= 216П(см3)
Ответ: V=216П(см3)

17.

Свойство объемов №1
Равные тела имеют равные объемы
Свойство объемов №2
Если тело составлено из нескольких тел, то
его объем равен сумме объемов этих тел.
Свойство объемов №3
Если одно тело содержит другое, то объем
первого тела не меньше объема второго.

18.

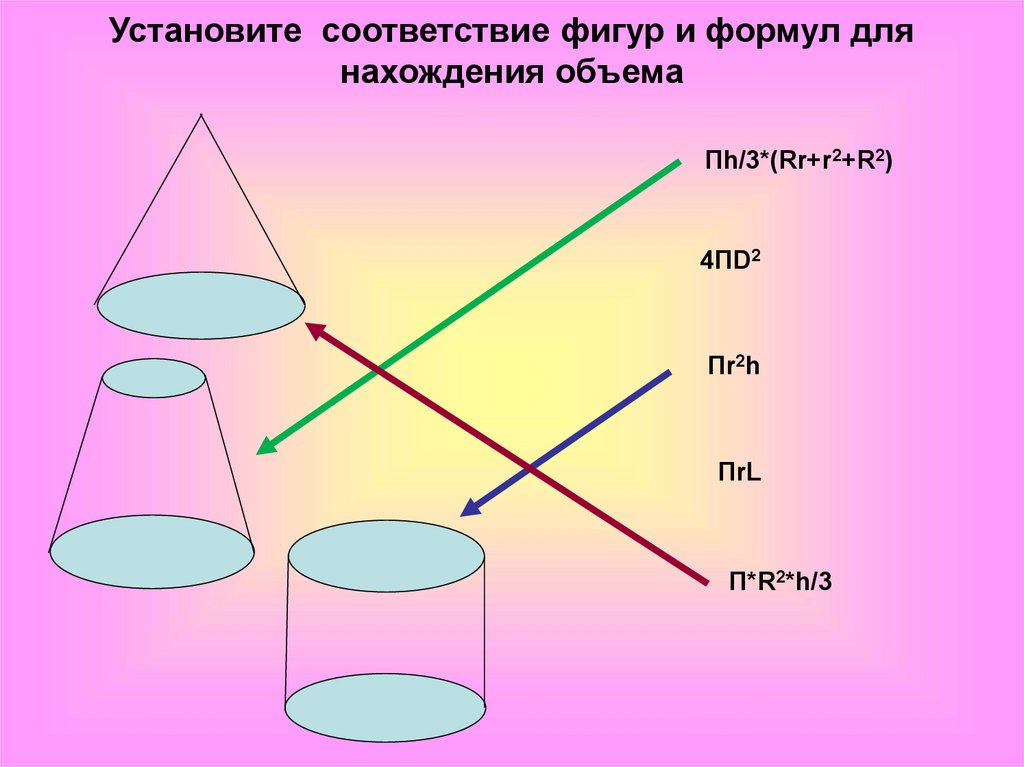
Установите соответствие фигур и формул для
нахождения объема
Пh/3*(Rr+r2+R2)
4ПD2
Пr2h
ПrL
П*R2*h/3

19.

Домашнее задание
П. 70, № 701,704,709, Д.К/р

20.

Библиография
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев
«Геометрия, 10-11», М., Просвещение, 2007
В.Я. Яровенко «Поурочные разработки по
геометрии», Москва, «ВАКО», 2006