Декартовая система координат

1. МОУ Дивногорская СОШ

2010 год

2. Давайте вспомним что же называется системой координат?

Системой координат
называется совокупность
одной, двух, трех или более
пересекающихся
координатных осей.
Точки, в которой эти оси
пересекаются– начала
координат .

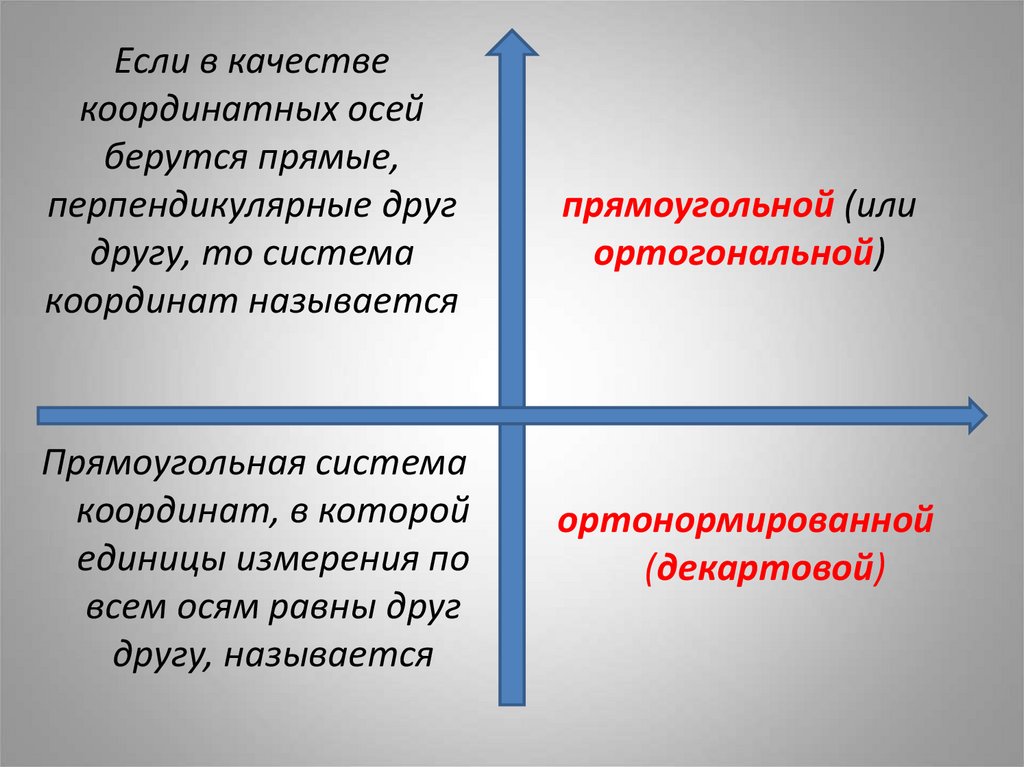
3. Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной

Если в качестве
координатных осей
берутся прямые,
перпендикулярные друг
другу, то система
координат называется
Прямоугольная система
координат, в которой
единицы измерения по
всем осям равны друг
другу, называется
прямоугольной (или
ортогональной)
ортонормированной
(декартовой)

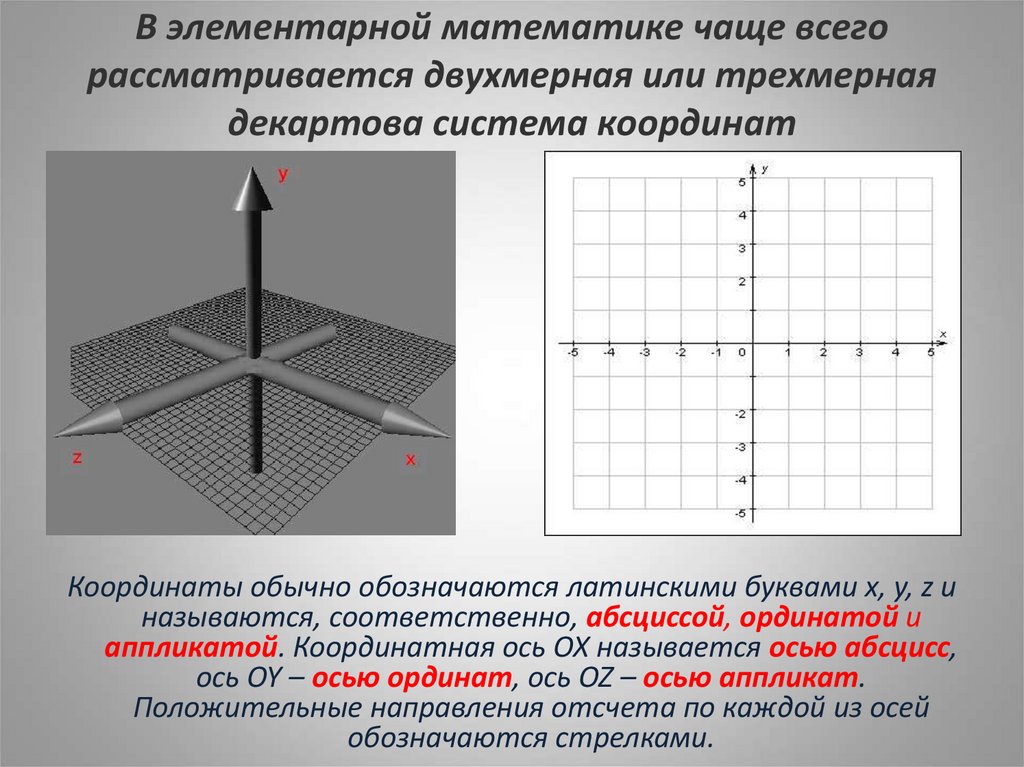
4. В элементарной математике чаще всего рассматривается двухмерная или трехмерная декартова система координат

Координаты обычно обозначаются латинскими буквами x, y, z и
называются, соответственно, абсциссой, ординатой и
аппликатой. Координатная ось OX называется осью абсцисс,
ось OY – осью ординат, ось OZ – осью аппликат.
Положительные направления отсчета по каждой из осей
обозначаются стрелками.

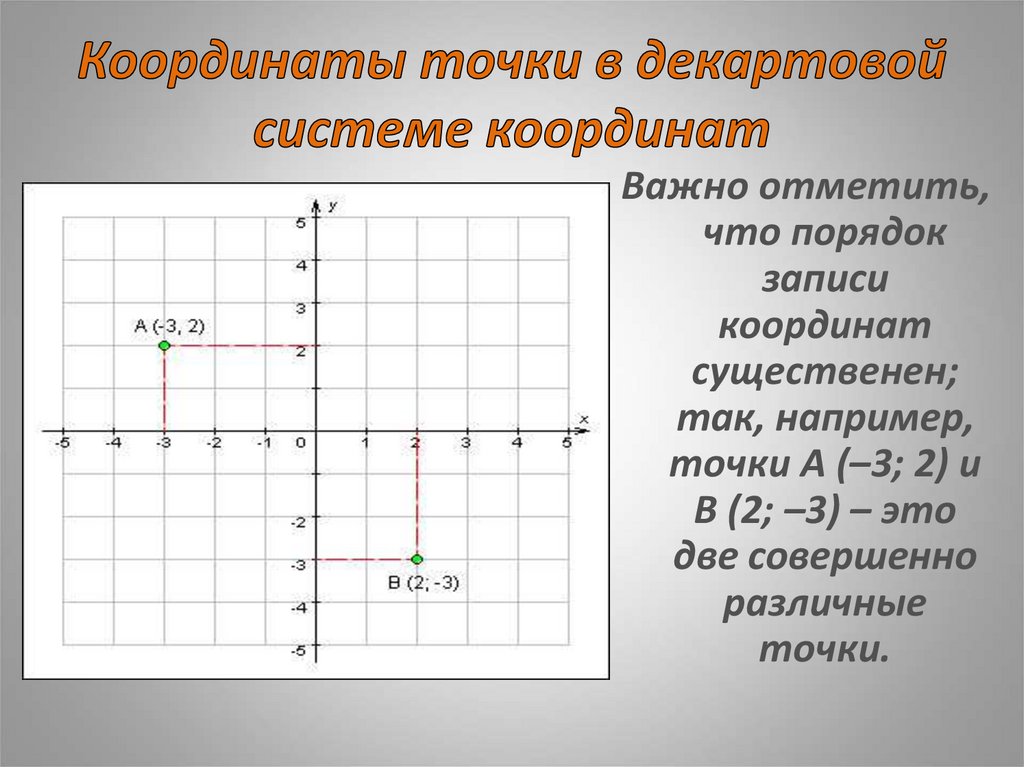
5. Координаты точки в декартовой системе координат

Важно отметить,
что порядок
записи
координат
существенен;
так, например,
точки A (–3; 2) и
B (2; –3) – это
две совершенно
различные
точки.

6. Координатные оси делят координатную плоскость на четыре квадранта (четверти). Точки, лежащие на осях координат, не принадлежат

ни
одному квадранту.
В двухмерной системе координат все точки,
лежащие над (под) осью OX, образуют верхнюю
(нижнюю) координатную полуплоскость. Все
точки, лежащие правее (левее) оси OY образуют
правую (левую) координатную полуплоскость.