Similar presentations:
Построение расписания минимальной длины для одностадийной системы с приборами различной производительности
1. Построение расписания минимальной длины для одностадийной системы с приборами различной производительности
ПОСТРОЕНИЕРАСПИСАНИЯ
МИНИМАЛЬНОЙ ДЛИНЫ
ДЛЯ ОДНОСТАДИЙНОЙ
СИСТЕМЫ С ПРИБОРАМИ
РАЗЛИЧНОЙ
ПРОИЗВОДИТЕЛЬНОСТИ
Исполнитель
Рожик Е.А.
Руководитель
Аснина А.Я.
2. Цель: разработка алгоритма построения расписания минимальной длины для системы с приборами различной производительности. Задачи: -рассмо
ЦЕЛЬ: РАЗРАБОТКА АЛГОРИТМА ПОСТРОЕНИЯЦЕЛИ И ЗАДАЧИ ВЫПУСКНОЙ
РАСПИСАНИЯ МИНИМАЛЬНОЙ ДЛИНЫ ДЛЯ
РАБОТЫ
СИСТЕМЫ С ПРИБОРАМИ РАЗЛИЧНОЙ
ПРОИЗВОДИТЕЛЬНОСТИ.
ЗАДАЧИ:
РАССМОТРЕТЬ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ
РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ОБСЛУЖИВАНИЯ
ТРЕБОВАНИЙ ПО ПРИБОРАМ;
ИЗУЧИТЬ МЕТОД ДЕКОМПОЗИЦИИ ДЛЯ ЗАДАЧИ
БОЛЕЕ ОБЩЕГО ВИДА;
ПЕРЕФОРМУЛИРОВАТЬ МЕТОД ДЛЯ ЗАДАЧИ
РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ;
ПРИМЕНИТЬ МЕТОД ДЛЯ РЕШЕНИЯ
ПОСТАВЛЕННОЙ ЗАДАЧИ;
ВЫВЕСТИ ФОРМУЛУ ЧИСЛА ПЕРЕХОДОВ С
ОДНОГО ПРИБОРА НА ДРУГОЙ ДЛЯ ЗАДАЧИ
РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ, РЕШАЕМОЙ
МЕТОДОМ ДЕКОМПОЗИЦИИ;
3. -показать, что с помощью метода декомпозиции получается распределение времени с минимально возможным переходов; -разработать конструктив
ЦЕЛИ И ЗАДАЧИ ВЫПУСКНОЙРАБОТЫ
ПОКАЗАТЬ, ЧТО С ПОМОЩЬЮ МЕТОДА
ДЕКОМПОЗИЦИИ ПОЛУЧАЕТСЯ РАСПРЕДЕЛЕНИЕ
ВРЕМЕНИ С МИНИМАЛЬНО ВОЗМОЖНЫМ
ПЕРЕХОДОВ;
РАЗРАБОТАТЬ КОНСТРУКТИВНЫЙ АЛГОРИТМ
ПОСТРОЕНИЯ РАСПИСАНИЯ;
РАЗРАБОТАТЬ ПРОГРАММУ РЕАЛИЗАЦИИ МЕТОДА
ДЕКОМПОЗИЦИИ И АЛГОРИТМА ПОСТРОЕНИЯ
РАСПИСАНИЯ С МИНИМАЛЬНЫМ ЧИСЛОМ
ПРЕРЫВАНИЙ;
РАЗРАБОТАТЬ МЕТОД ПОСТРОЕНИЯ РАСПИСАНИЯ
ДЛЯ СИСТЕМЫ С РАЗЛИЧНЫМИ МОМЕНТАМИ
ПОСТУПЛЕНИЯ ТРЕБОВАНИЙ.
4. Системы с идентичными приборами
СИСТЕМЫ С ИДЕНТИЧНЫМИПРИБОРАМИ
n
x
j 1
ij
m
x
ij
T
i = 1,..,n
T
j = 1,..,n
tj
j = 1,..,n
i 1
m
x
i 1
ij
xij 0
i = 1,..,n j = 1,..,n
T min
xij
tj
– время, в течение которого j е требование будет обслуживаться iм прибором;
длительность обслуживания jго требования.
Tmin = T* max( t1 ,
t1 t 2 ... t n
n
t
j 1
m
j
)
при условии, что
5.
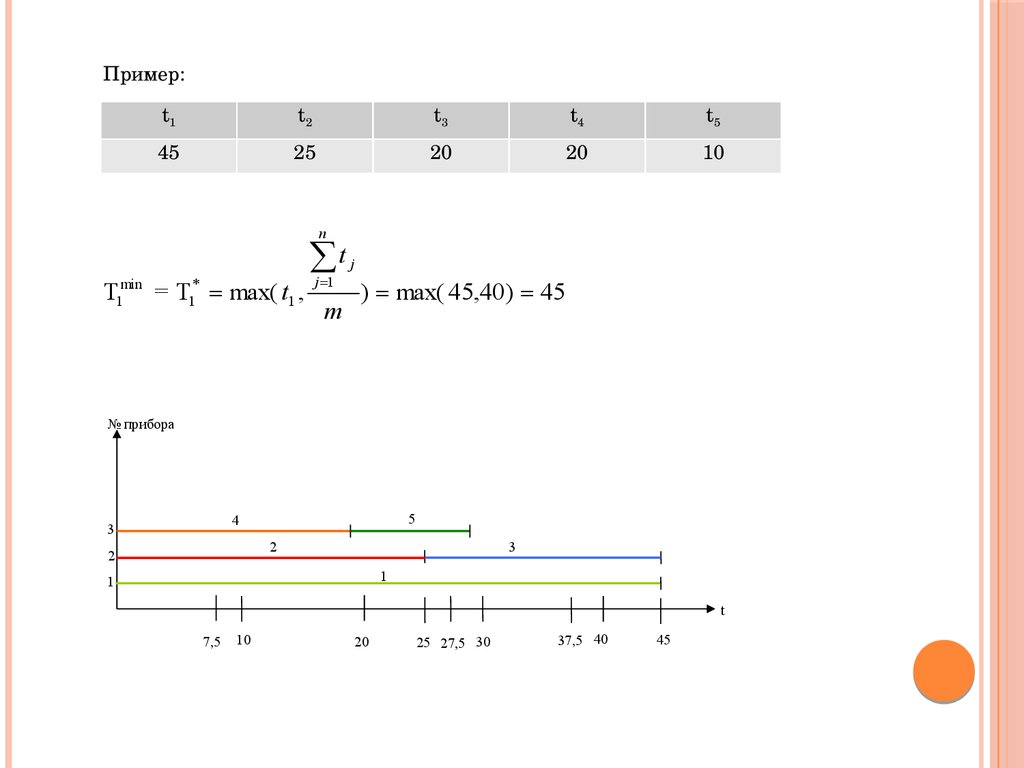
Пример:t1
t2
t3
t4
t5
45
25
20
20
10
n
min
1
T
= T max( t1 ,
*
1
t
j 1
m
j
) max( 45,40) 45
№ прибора
5
4
3
2
2
3
1
1
t
7,5
10
20
25 27,5 30
37,5 40
45
6.
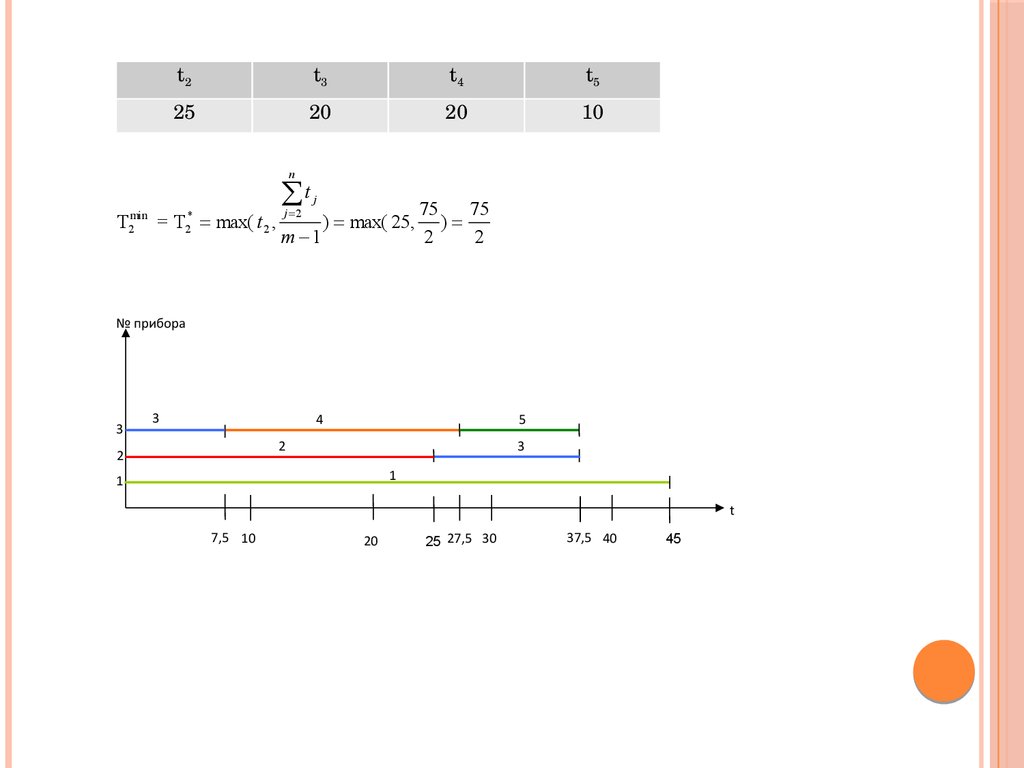
t2t3
t4
t5
25
20
20
10
n
min
2
T
= T max( t 2 ,
*
2
t
j 2
j
m 1
) max( 25,
75
75
)
2
2
№ прибора
3
3
4
5
2
2
3
1
1
t
7,5 10
20
25 27,5 30
37,5 40
45
7.
n(1)
(2)
x
j 1
m
ij
x
i 1
m
xij
t
i 1
ij
T
Системы с различными
приборами
i = 1,…,m;
T
j = 1,..,n
1
j = 1,..,n
ij
xij 0
i = 1,…,m, j = 1,..,n
T min
xij – время, в течение которого j - е требование будет обслуживаться i-м
прибором;
t ij - длительность обслуживания j-го требования на i-м
приборе.
T- длина расписания.
(1) – общее время занятости i-го прибора не превосходит T;
(2) – общее время обслуживания j-го требования не превосходит T.
8.
Системы с приборами различнойпроизводительности
tj
- длительность обслуживания j - го требования на приборе с самой низкой производительностью.
i
- показывает, во сколько раз быстрее обслуживается требование на i-м приборе по сравнению
с наименее производительным.
Тогда t ij
n
x
j 1
T
i = 1,..,m
(1)
ij
T
j = 1,..,n
(2)
j = 1,..,n
(3)
i = 1,..,m j = 1,..,n
(4)
i 1
m
x
i 1
i
- длительность обслуживания j-го требования на i-м приборе.
ij
m
x
tj
i
ij
tj
xij 0
T min
(5)
9.
Утверждение. Если 1 2 ... m ; t1 t 2 ... t nn
m 1
min F1max
ti t j
t1 t1 t 2
j 1
T max( ,
,..., mi 11 , m ) T *
1 1 2
i i
i 1
Заметим, что
,то
i
i 1
=1, получаем формулу для идентичных приборов:
n
F1max T max( t j ,
t
j 1
m
j
)
10.
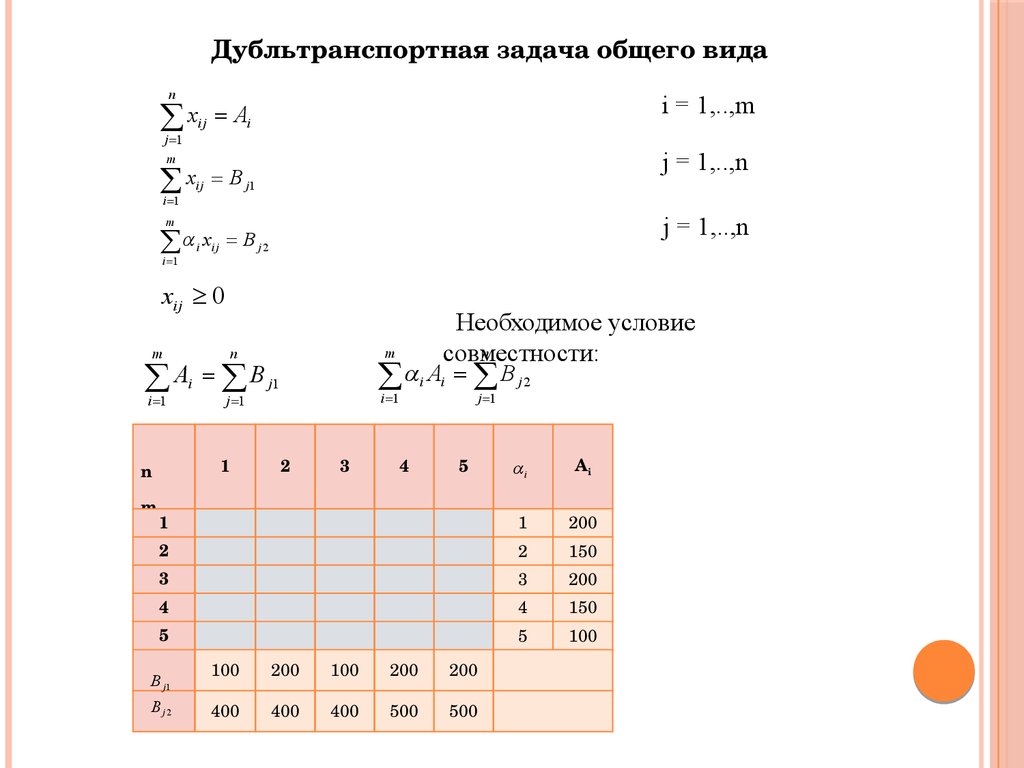
Дубльтранспортная задача общего видаn
Ai
i = 1,..,m
xij B j1
j = 1,..,n
x
j 1
ij
m
i 1
m
x
i
j = 1,..,n
B j2
ij
i 1
xij 0
m
i 1
m
n
A B
i
j 1
Необходимое условие
n
совместности:
A B
j1
i
i 1
i
j 1
j2
1
2
3
4
5
i
Ai
1
1
200
2
2
150
3
3
200
4
4
150
5
5
100
100
200
100
200
200
400
400
400
500
500
n
m
B j1
B j2
11.
Для всех j = 1…n-1Метод
декомпозиции
B
j2
Шаг 1.
s j max {ai
}
i
B
j
1
Определяется
B j 2 a s B j1
Шаг 2. Вычисляются
x kj
ak as
Шаг 3.
Если
x sj As
k j min {ai
i
B j1
}
и
x sj B j1 x kj
x kj Ak
AsH As x js
B j2
, то
и
AkH Ak x ks
и переход j = j +
1.
x sj As
Шаг 4. Если
x sj As
AsH 0
B Hj1 B j1 x sj
B Hj2 B j 2 a s x sj
s Hj s j 1
, то
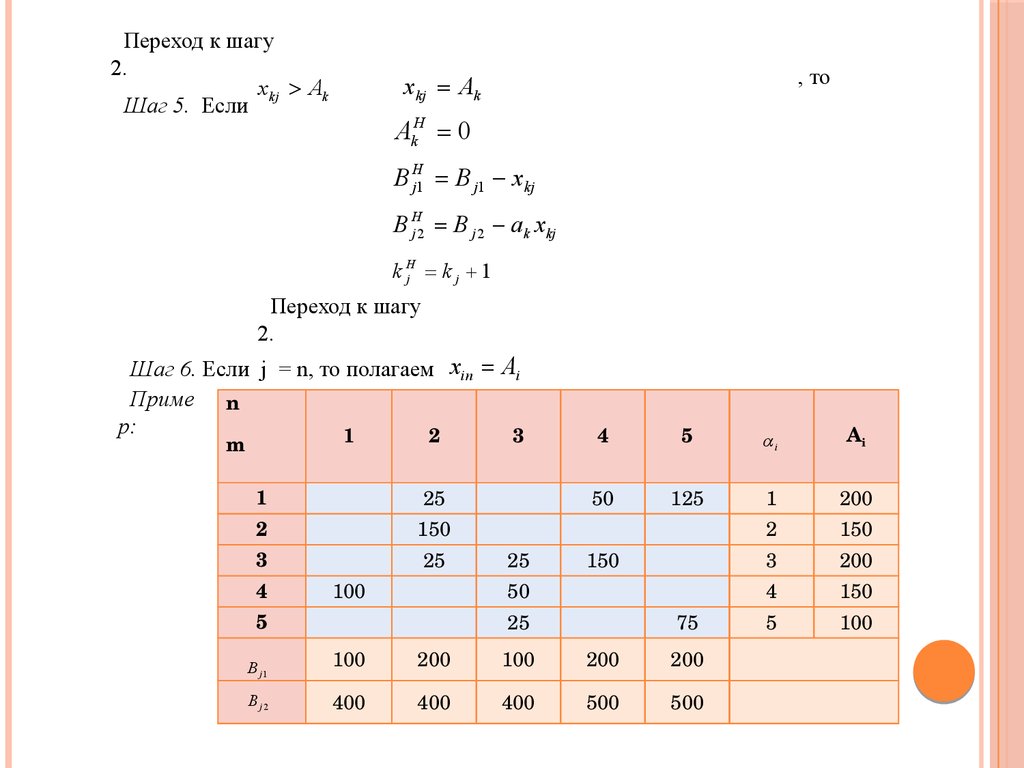
12.
Переход к шагу2.
x kj Ak
Шаг 5. Если
, то
x kj Ak
AkH 0
B Hj1 B j1 x kj
B Hj2 B j 2 a k x kj
k Hj k j 1
Переход к шагу
2.
Шаг 6. Если j = n, то полагаем xin Ai
Приме n
р:
1
2
3
m
4
5
i
Ai
1
25
50
125
1
200
2
150
2
150
3
25
25
150
3
200
4
100
50
4
150
5
25
75
5
100
B j1
100
200
100
200
200
B j2
400
400
400
500
500
13.
Задача распределениявремени
n
x
j 1
ij
n
x
j 1
m 1 j
m 1
x
i 1
ij
Tm 1 (n m)T *
x
i 1
Где:
j = 1,..,n
T
m 1
i
i = 1,..,m
T
ij
tj
Аi T *
Am 1 Tm 1
B j1 T *
B j2 t j
j = 1,..,n
14.
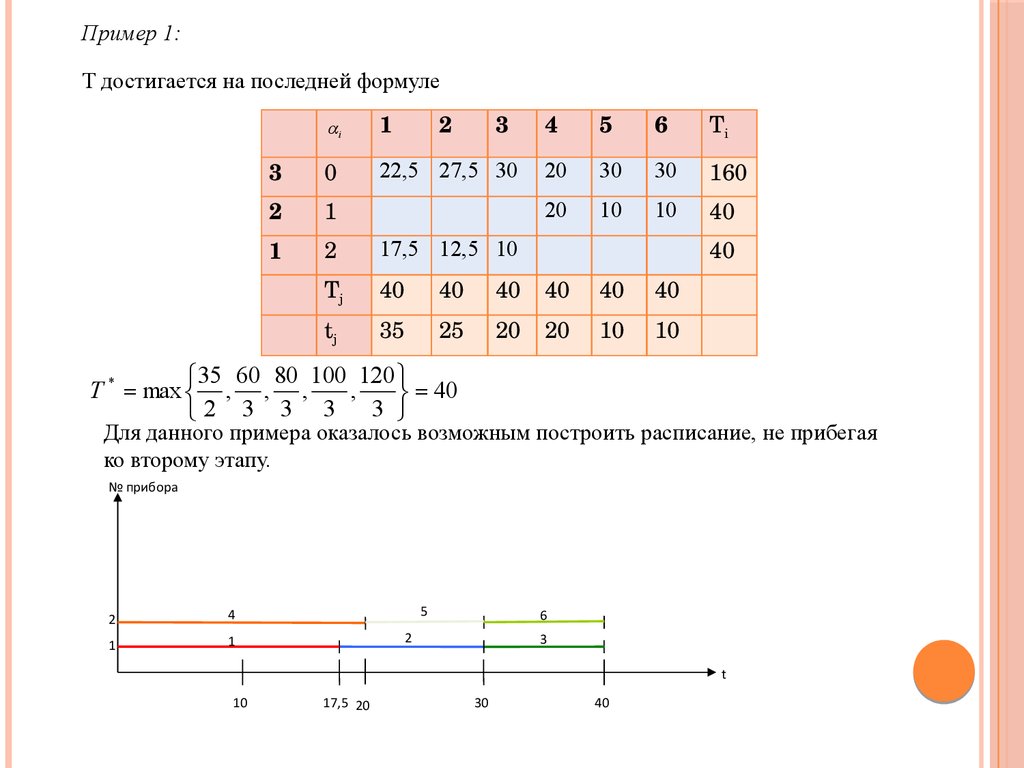
Пример 1:Т достигается на последней формуле
i
1
2
3
4
5
6
Ti
3
0
22,5 27,5 30
20
30
30
160
2
1
20
10
10
40
1
2
17,5 12,5 10
Tj
40
40
40
40
40
40
tj
35
25
20
20
10
10
40
35 60 80 100 120
T * max , , ,
,
40
3
2 3 3 3
Для данного примера оказалось возможным построить расписание, не прибегая
ко второму этапу.
№ прибора
2
4
1
1
5
6
2
3
t
10
17,5 20
30
40
15.
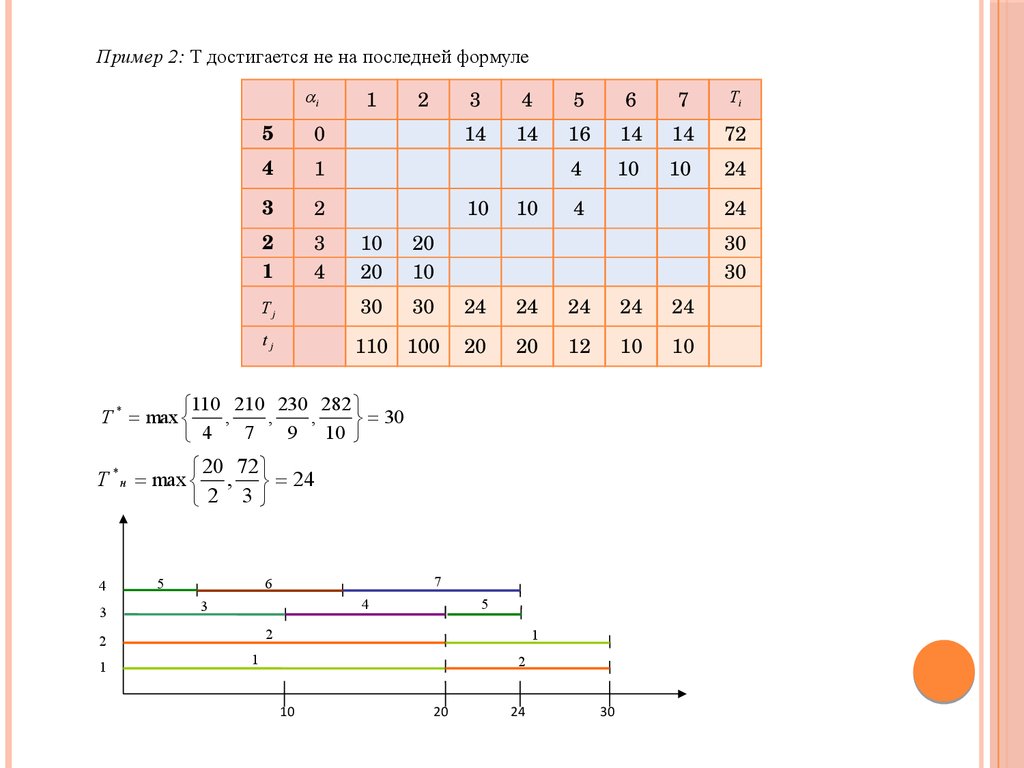
Пример 2: Т достигается не на последней формулеi
1
2
3
4
5
6
7
Ti
14
14
16
14
14
72
4
10
10
24
5
0
4
1
3
2
10
10
4
2
1
3
4
10
20
20
10
30
30
Tj
30
30
24
24
24
24
24
tj
110 100
20
20
12
10
10
24
110 210 230 282
T * max
,
,
,
30
7
9 10
4
20 72
T * н max , 24
2 3
4
3
5
5
4
3
2
2
1
7
6
1
1
2
10
20
24
30
16.
Алгоритм построения расписания0. Полагаем t=0
1.
Ti xij
j
T j xij
i
2. T max{Ti , T j }
3. i T Ti , j T T j
Строка, у которой i 0, называется плотной строкой
Столбец, у которого j 0, называется плотным столбцом
4. В каждой плотной строке и в каждом плотном столбце выделяется ровно
один элемент. И в каждой строке и в каждом столбце, не являющихся
плотными, выделяется не более одного элемента. Выделение нелднозначно,
обозначим ( xij )
5. Определяем интервал, на котором будем строить расписание
min{( x ij ) i ; ( xij ) j ; i ; j }, i
j
если нет выделения в столбце;
если нет выделения в строке;
17.
6. На интервале (t , t ) требования распределяются на обслуживание в соответствиис таблицей, полученной на первом этапе.
7. Преобразуем матрицу
( xij ) [ xij ] , xij
не изменится. Если какоето xij , будет «дырка»
8. Полагаем t t и переходим к шагу 1.
18.
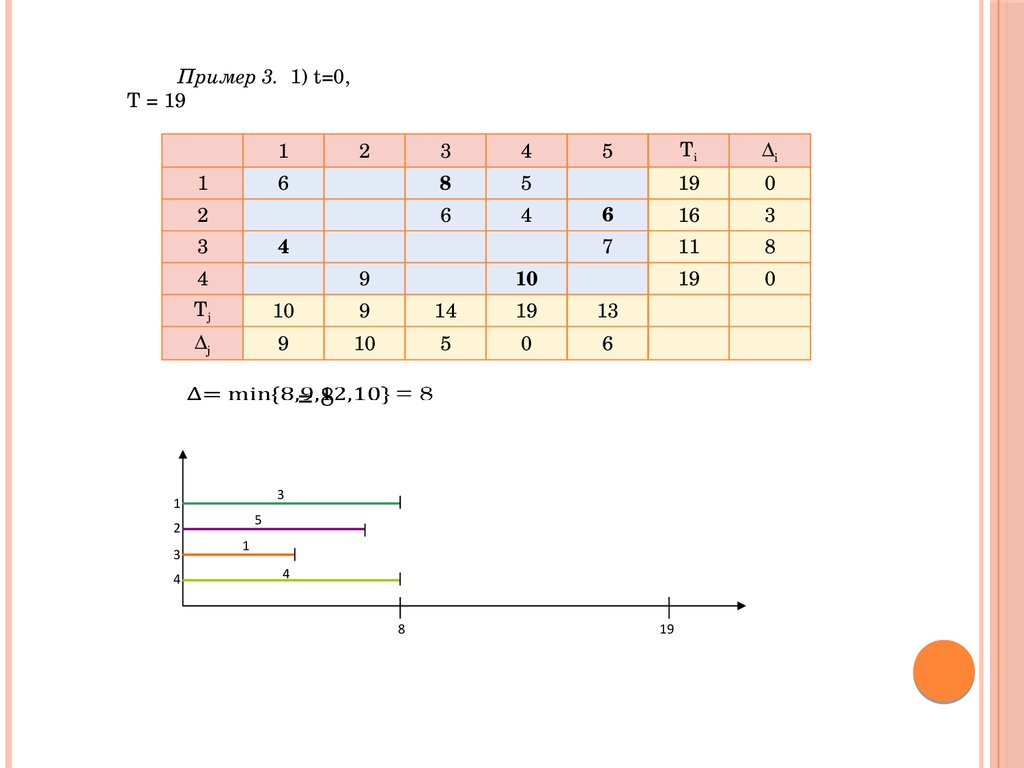
Пример 3. 1) t=0,T = 19
1
2
3
4
5
Ti
Δi
1
6
8
5
19
0
2
6
4
6
16
3
3
4
7
11
8
4
9
10
19
0
Tj
10
9
14
19
13
Δj
9
10
5
0
6
= 8
3
1
5
2
3
4
1
4
8
19
19.
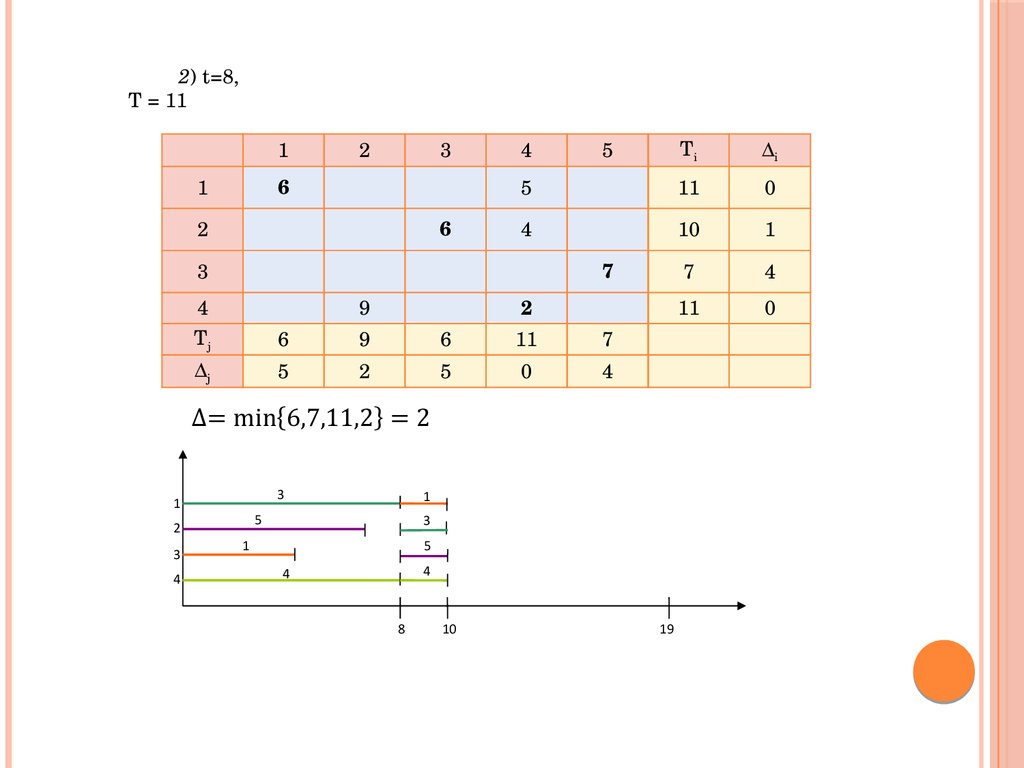
2) t=8,T = 11
5
Ti
Δi
5
11
0
10
1
7
7
4
1
2
1
6
2
6
4
3
3
4
4
9
2
11
0
Tj
6
9
6
11
7
Δj
5
2
5
0
4
3
1
5
2
3
4
1
3
1
5
4
4
8
10
19
20.
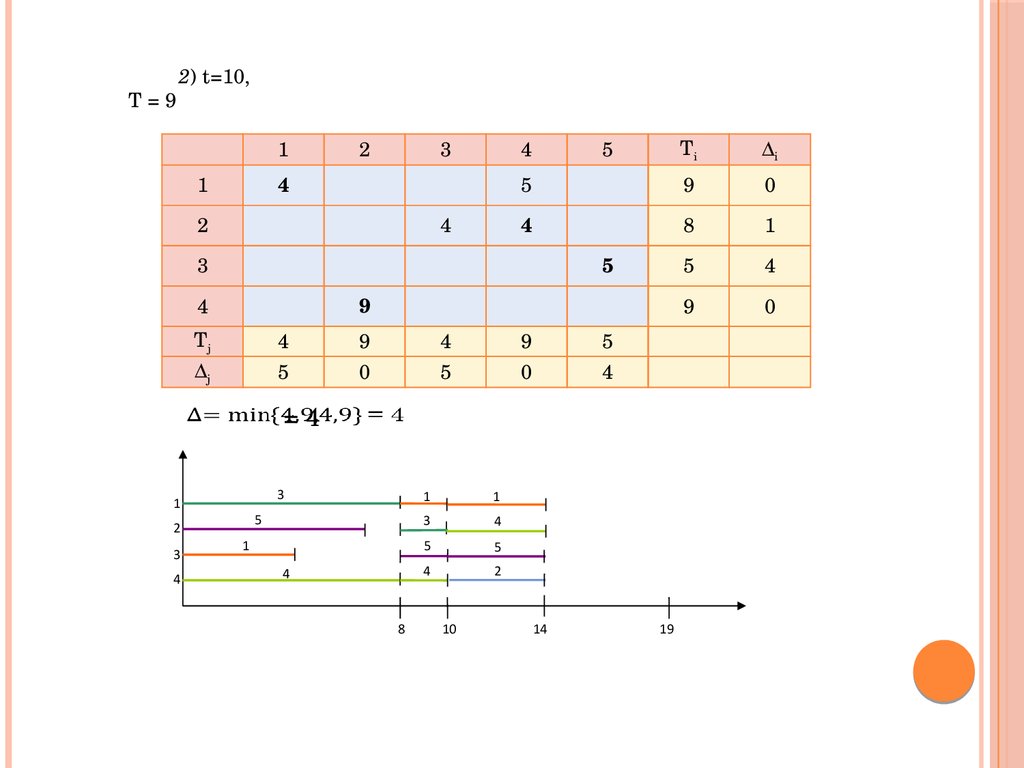
T = 92) t=10,
Δi
5
9
0
8
1
5
5
4
9
0
1
4
2
4
4
4
9
Tj
4
9
4
9
5
Δj
5
0
5
0
4
= 4
3
1
5
2
4
Ti
2
3
5
1
3
3
4
1
4
8
1
1
3
4
5
5
4
2
10
14
19
21.
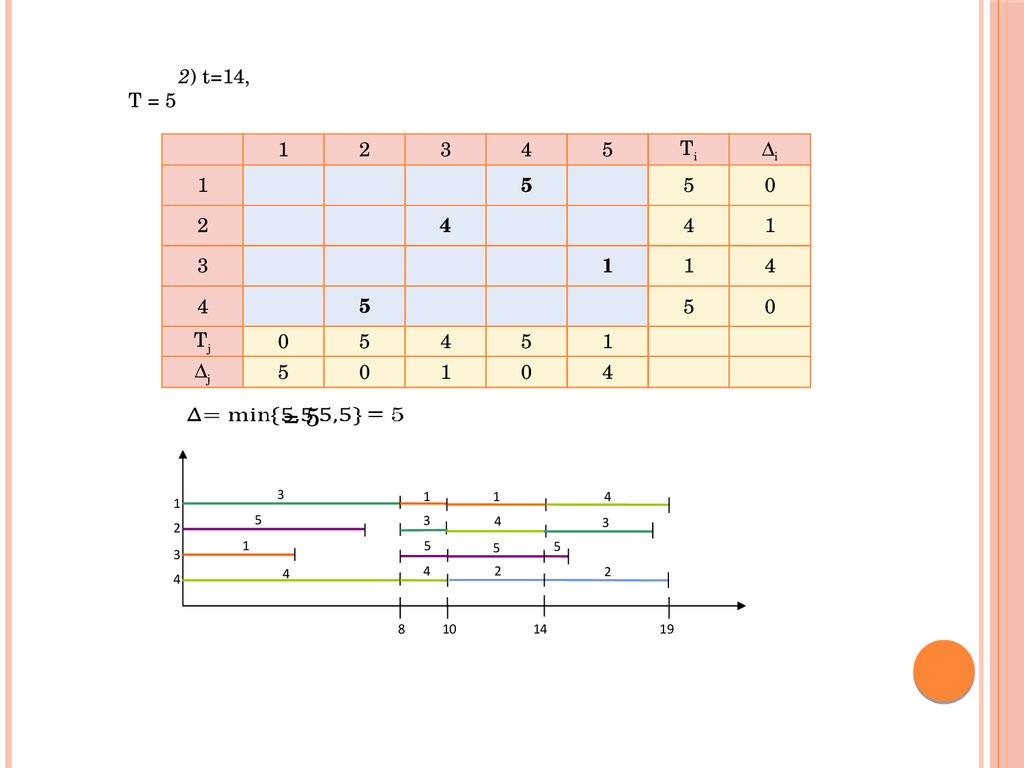
T = 52) t=14,
1
1
3
4
4
5
Ti
Δi
5
5
0
4
1
1
1
4
5
0
4
5
Tj
0
5
4
5
1
Δj
5
0
1
0
4
= 5
3
1
5
2
4
3
2
3
2
1
4
8
1
1
4
3
4
3
5
5
4
2
10
5
2
14
19
22.
Заметим, если достигает своего максимума не на последней формуле, топри использовании вышеприведенного алгоритма построения расписания и
алгоритма декомпозиции №1, приборы будут загружены неплотно:
Если же использовать алгоритм декомпозиции №2, приборы будут
загружены плотно:
23.
Построение расписания для задачи с различными моментами поступлениятребований
dj
время поступления jго требования в
систему
множества требований, поступивших в моменты
I 0 ,..., I r
времени
d 0 ,...d r
Алгоритм распределения времени и построения расписания
0. Пусть k = 0. Введем множество I . I . I k 1,2,...m
Ik .
1. Вычисляем оптимальное время обслуживания T для множества требований
2. По алгоритму декомпозиции распределяем время для множества I k I k I
на интервале [d k , d k T ].
Строим расписание.
3. Если T d k 1 d k , то расписание на интервале[d k , d k T ] оставляем неизменным,
переход к шагу 5. Иначе переход к шагу 4.
4. Изменяем полученное расписание. На интервале [d k , d k 1 ] расписание оставляем
неизменным. А из требований, обслуживающихся на интервале [d k 1 , d k T ]
m
k
составляем множество I . Полагаем t j ij i ,
i 1
где ijk время
обслуживания jго требования на iм приборе на интервале [d k 1 , d k T ] для j из I .
5. Если k<r, то k=k+1 и переход к шагу 1, иначе останов.
24.
Пример 4.1 этап. T=16, достигается на первой
формуле.
1
2
3
4
5
6
7
8
Ti
4 0
3 1
16
16
2 2
1 3
16
16
16
0
0
0
0
8
8
8
8
16
16
16
16
48
12
8
4
16
i
dj
Tj
tj
Пересчитываем T для оставшихся требований, поступивших в
момент 0.
Т=8, достигается на последней формуле.
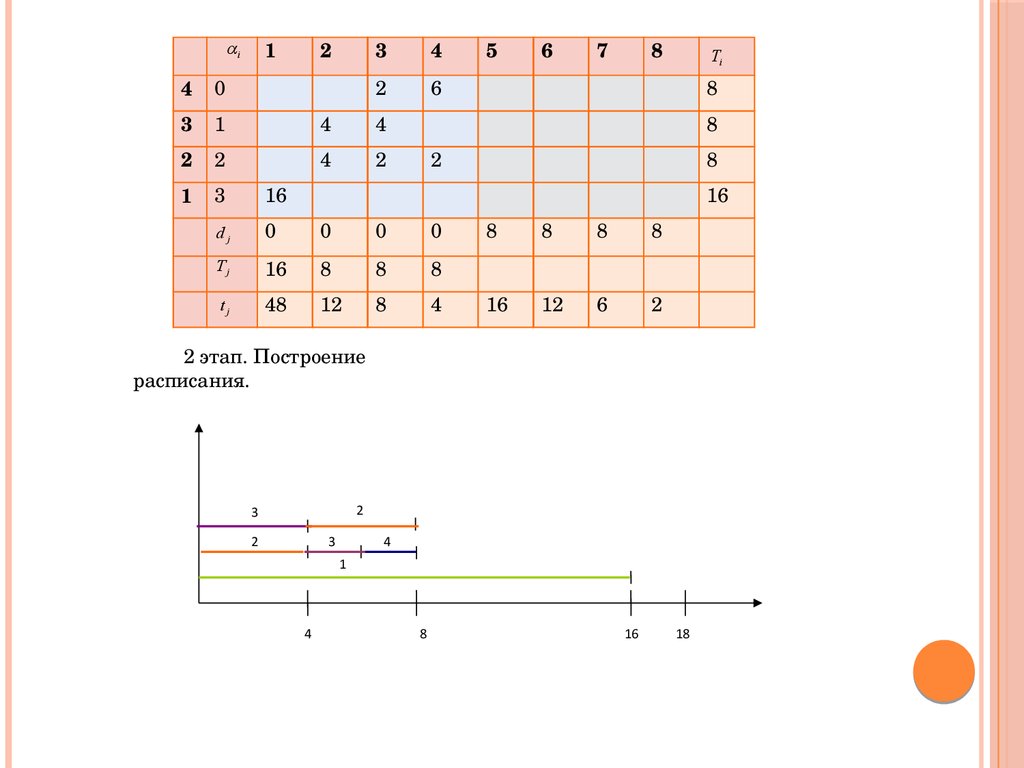
25.
i1
2
3
4
5
6
7
8
Ti
4
0
2
6
8
3
1
4
4
8
2
2
4
2
2
8
1
3
16
16
dj
0
0
0
0
8
8
8
8
T j
16
8
8
8
t j
48
12
8
4
16
12
6
2
2 этап. Построение
расписания.
2
3
2
3
4
1
4
8
16
18
26.
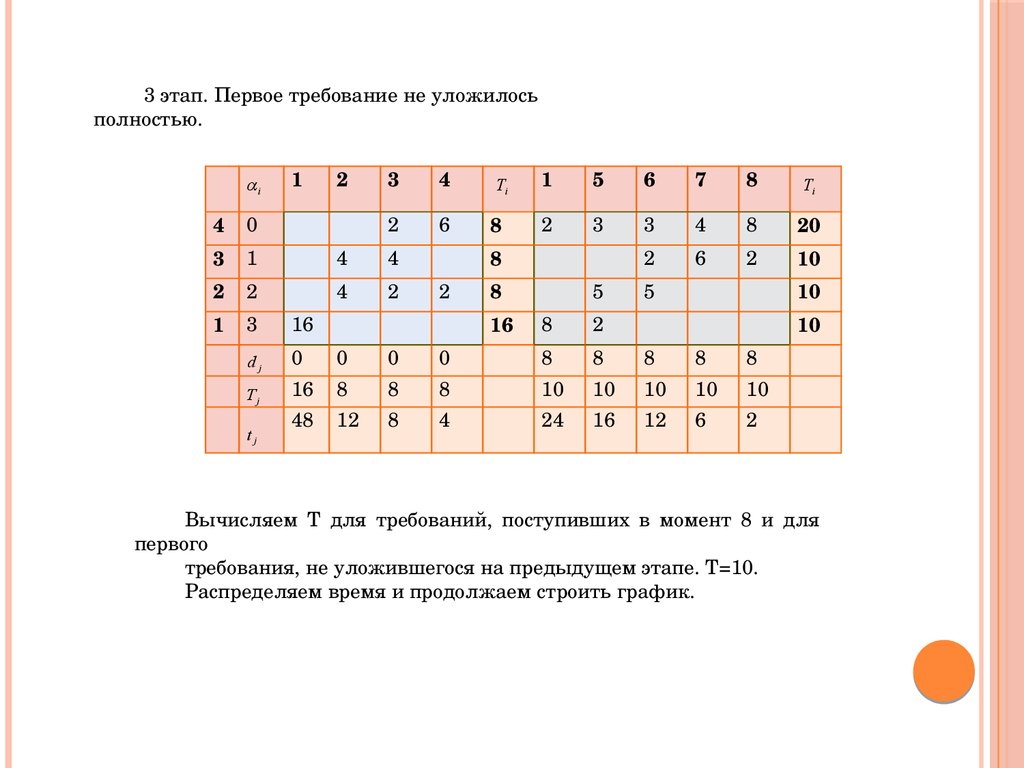
3 этап. Первое требование не уложилосьполностью.
i
1
2
3
4
Ti
1
5
6
7
8
Ti
4
0
2
6
8
2
3
3
4
8
20
3
1
4
4
8
2
6
2
10
2
2
4
2
2
8
5
5
10
1
3
16
16
8
2
10
d j
0
0
0
0
8
8
8
8
8
j
T
16
8
8
8
10
10
10
10
10
48
12
8
4
24
16
12
6
2
tj
Вычисляем Т для требований, поступивших в момент 8 и для
первого
требования, не уложившегося на предыдущем этапе. Т=10.
Распределяем время и продолжаем строить график.
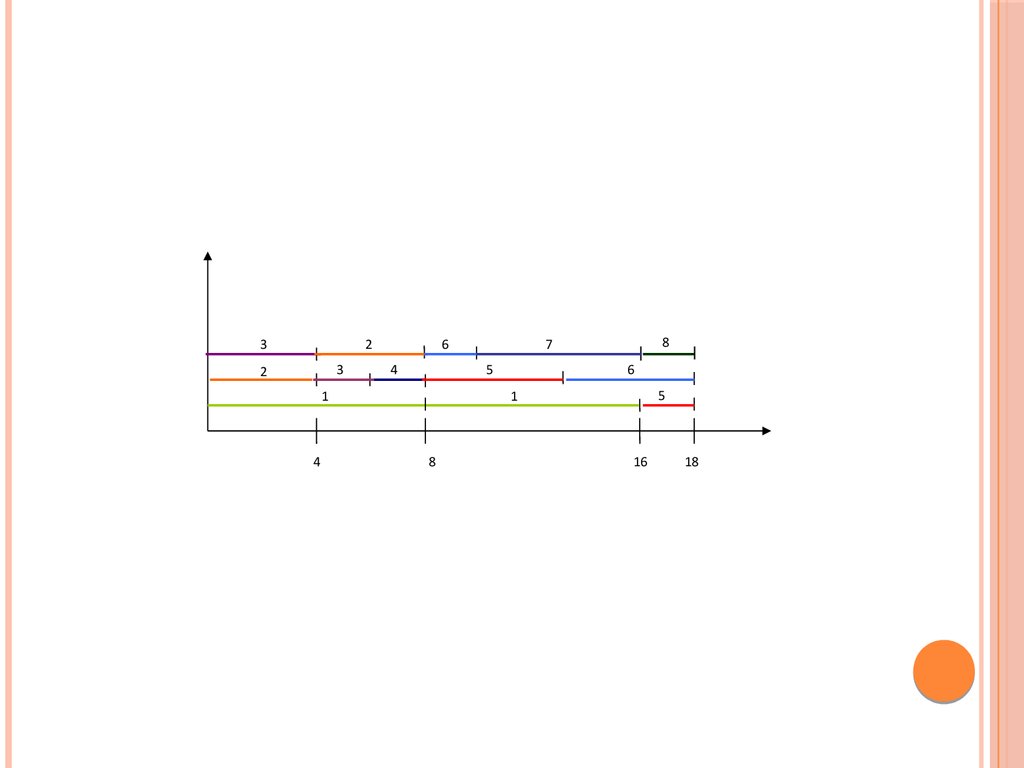
27.
32
3
2
6
4
5
1
4
8
7
6
5
1
8
16
18
28.
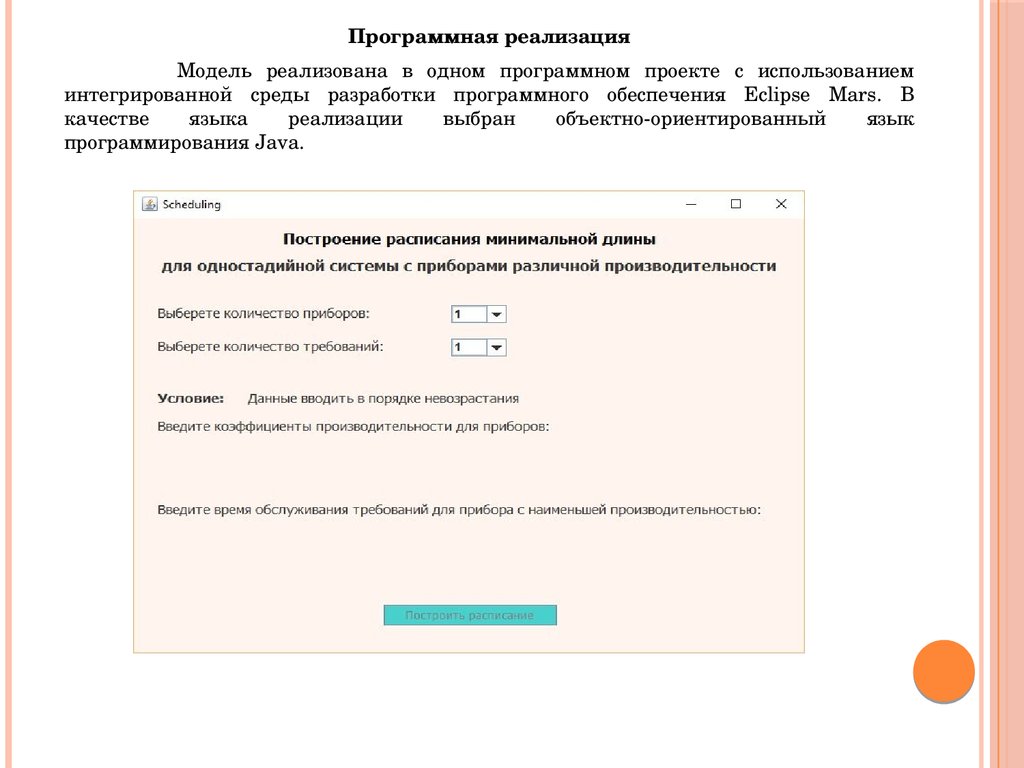
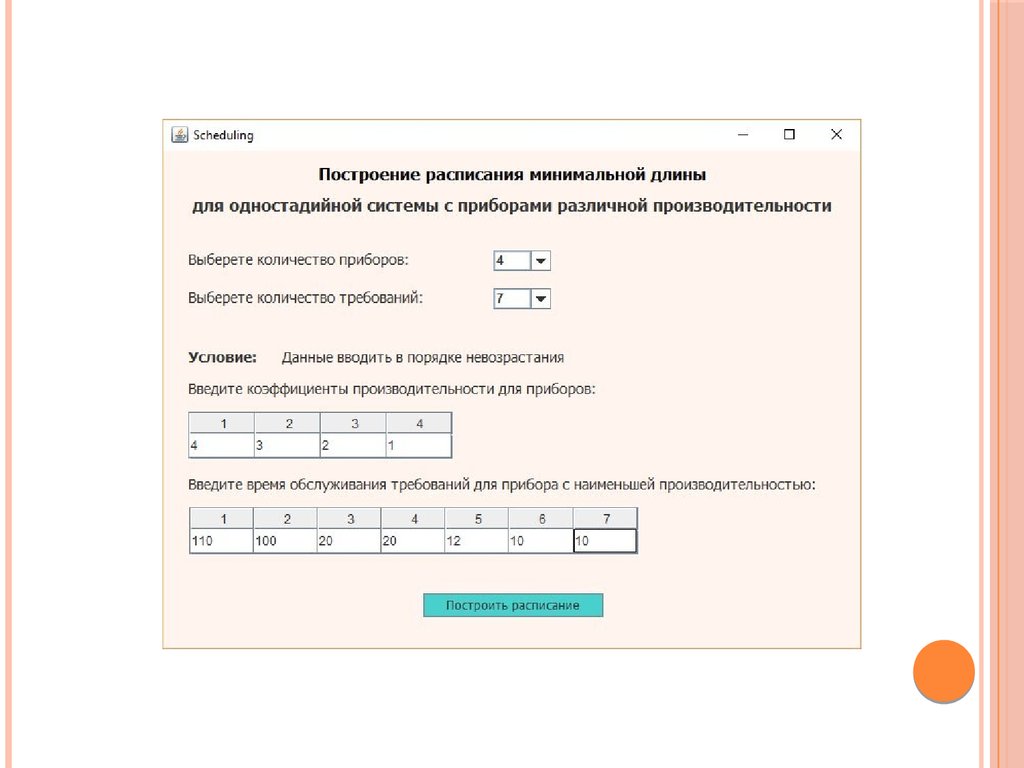
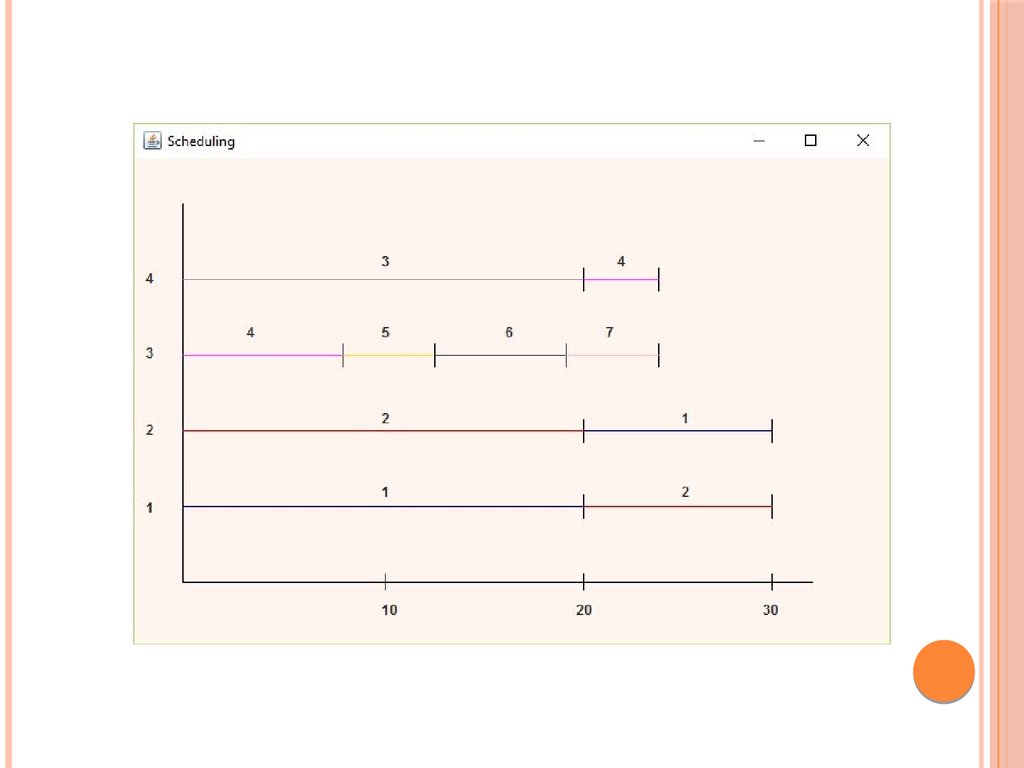
Программная реализацияМодель реализована в одном программном проекте с использованием
интегрированной среды разработки программного обеспечения Eclipse Mars. В
качестве
языка
реализации
выбран
объектноориентированный
язык
программирования Java.














 mathematics
mathematics electronics
electronics








