Разложение по переменным. ДМ 2. ДНФ и КНФ

1. Дискретная математика

2.

ДНФ и КНФ.
Разложение функции по переменным
Формула алгебры логики – запись
суперпозиции логических функций с
использованием знаков переменных,
скобок и знаков логических функций
(логических вязок):
1 , 2 , 3 , , ~ , , I , .
Порядок записи логических связок
определяет иерархию, на основании
которой расставляются скобки.

3. Расстановка скобок

Каждая подформула окружается скобками.
Скобки можно не ставить, если они внешние.
x y x y.
Отрицание связывает сильнее всех.
x y x y.
Конъюнкция связывает сильнее остальных
x y z x z y
x y z x z y.

4. Элементарной конъюнкцией называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более

одного раза.
x, x y , x y z.
Дизъюнктивной нормальной
формой (ДНФ) называется
дизъюнкция элементарных
конъюнкций.
x x y x y z.

5.

Дизъюнктивная форма будет
совершенной (СДНФ), если
каждая элементарная
конъюнкция содержит все
наименования переменных.
xyz x yz xyz x yz

6. Элементарной дизъюнкцией называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более

одного раза.
x, x y , x y z.
Конъюнктивной нормальной
формой (KНФ) называется
конъюнкция элементарных
дизъюнкций.
x x y x y z .

7.

Конъюнктивная форма будет
совершенной (СКНФ), если
каждая элементарная
дизъюнкция содержит все
наименования переменных.
x y z x y z x y z

8. Разложение функции по переменным

Введем обозначение
x x , x x.
0
1
Замечание:
1
,
x
x
0 , x

9. Разложение функции по переменным

Доказательство:
x 0 , 0 , x 0 0 1,
0
x 1, 1, x 1 1,
1
1
0
x 0, 1, x 0 0,
x 1, 0, x 1 1 0.

10. Теорема о разложении функции по переменным

Всякая логическая функция
y f x1 , x2 , ..., xn
может быть разложена по
переменным
x1 , x2 , ..., xm , m n

11. Разложение функции по переменным

то есть представлена в виде:
f x1 , x2 , ... , xm , ... , xn
1 2 ... m
1
x1
2
m
x2 ... xm
f 1 , 2 , ... , m , xm 1 , ... , xn

12. Разложение функции по переменным

Дизъюнкция в правой части равенства
берется по всем наборам параметров.
1 , 2 , ... , m 0,1 .
Всего частей разложения будет
m
2 .
Рассмотрим разложение по одной
переменной и по всем переменным.

13. Разложении по одной переменной

При m =1 в разложении будет ровно 2
конъюнкции, соединенные
дизъюнкцией.
f x , y , z x f 0, y , z x f 1, y , z
0
x f 0, y , z x f 1, y , z .
1

14. Пример 1:

Разложить по переменной х
функцию, заданную формулой.
f x , y , z x z x y

15. Пример 2:

Разложить по переменной х
функцию, заданную векторстолбцом
f x , y , z 01001110
Т

16. Разложении по всем переменным

При m = n в разложении будет ровно
столько частей, сколько единичных
наборов у функции. Каждая часть
соответствует одному единичному набору:
То есть для всех наборов 1 2 3 ,
таких что
f x , y , z
f 1 , 2 , 3 1 :
x
y z f 1 , 2 , 3
1 2 3
f 1 , 2 , 3 1

17. Правило построения СДНФ из вектор-столбца

Функция задана
таблицей
1. Выбрать все
единичные
наборы
значений
аргументов
х
у
F(x,y)
0
0
1
0
1
0
1
0
1
1
1
1

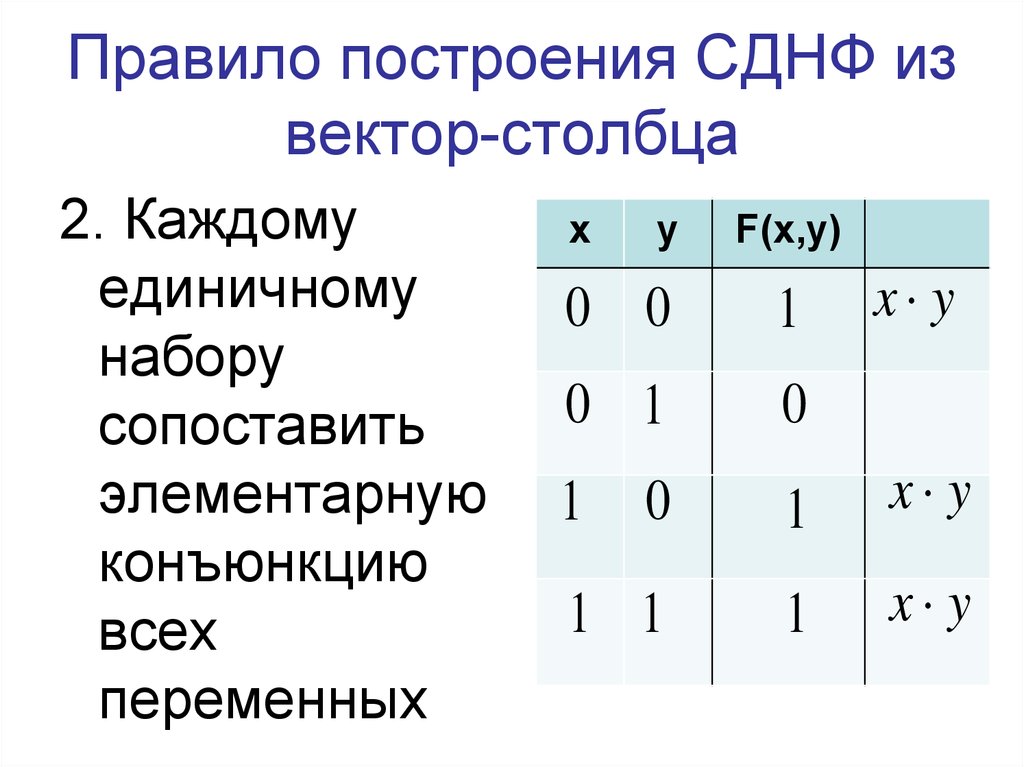
18. Правило построения СДНФ из вектор-столбца

2. Каждому
единичному
набору
сопоставить
элементарную
конъюнкцию
всех
переменных
х
у
F(x,y)
x y
0 0
1
0 1
0
0
1
x y
1 1
1
x y
1

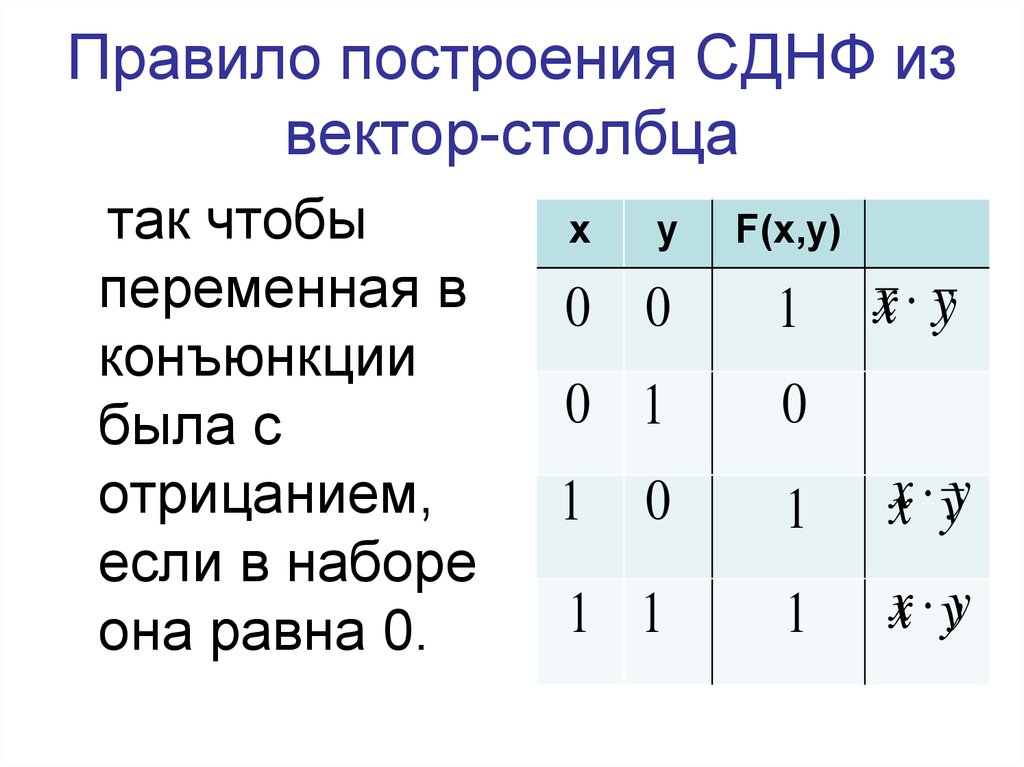
19. Правило построения СДНФ из вектор-столбца

так чтобы
переменная в
конъюнкции
была с
отрицанием,
если в наборе
она равна 0.
х
у
F(x,y)
x y
0 0
1
0 1
0
0
1
xx yy
1 1
1
x yy
1

20. Правило построения СДНФ из вектор-столбца

3. Соединить полученные
конъюнкции знаком
дизъюнкции
xy x y xy