Similar presentations:
Разложение функций по переменным
1.
Разложение функций по переменным.Нормальные формы
Процесс
замены
громоздких
булевых
функций равносильными, но более простыми,
путём использования законов алгебры логики,
называется минимизацией булевых функций.
Для алгебры логики справедливы законы,
которые аналогичны законам действия с
множествами.
Минимизировать булевы функции надо,
приводя их к нормальной форме.
2.
Элементарной конъюнкцией (дизъюнкцией)называется
выражение,
состоящее
из
конечного числа переменных и их отрицаний,
взятых в этом выражении не более одного раза
и
разделённых
операциями
конъюнкции
(дизъюнкции):
s
y i , где yi xi или x i , например x1 x 2 x 3 i 1
элементарная конъюнкция;
s
y i , где yi xi или x i ,например x1 x2 x 3 i 1
элементарная дизъюнкция;
3.
Дизъюнктивной(конъюнктивной)
нормальной формой называется дизъюнкция
(конъюнкция) конечного числа элементарных
конъюнкций (дизъюнкций).
Нормальная
форма
называется
совершенной, если в каждой её элементарной
дизъюнкции (конъюнкции) представлены все
переменные, входящие в данную функцию
(либо сами, либо с отрицанием). Например, для
функции F ( x1 , x2 , x3 ) x1 x2 x 3 x1 x 2 x3 данное
логическое выражение является совершенной
ДНФ, сокращённо СДНФ.
4.
Любая булева функция, не являющаясятождественным нулём или единицей, имеет
только одну СДНФ с точностью до
расположения переменных.
х1 х2 х3 F
0 0 0 0
0 0 1 0
Задача. Пусть при n= 3
0 1 0 1
булева функция задана таблицей 0 1 1 1
истинности. Составить СДНФ
1 0 0 0
и СКНФ для данной функции.
1 0 1 0
1 1 0 1
1 1 1 0
5.
Решение. СДНФ: по строкам, х1 х2 х3в которых булева
функция
0 0 0
принимает значение 1, составляем 0 0 1
элементарные
конъюнкции, 0 1 0
которые затем
объединяем
0 1 1
дизъюнкциями. В конъюнкцию
1 0 0
входит сама переменная, если
1 0 1
её значение в данной строке
1 1 0
равно 1, и отрицание этой
1 1 1
переменной, если её значение равно 0.
F
0
0
1
1
0
0
1
0
F ( x1 , x2 , x3 ) x1 x2 x 3 x1 x2 x3 x1 x2 x 3
6.
Решение. СКНФ: по строкам, х1 х2 х3 Fв которых булева
функция
0 0 0 0
принимает значение 0, составляем 0 0 1 0
элементарные
дизъюнкции, 0 1 0 1
которые затем
объединяем
0 1 1 1
конъюнкциями. В дизъюнкцию
1 0 0 0
входит сама переменная, если
1 0 1 0
её значение в данной строке
1 1 0 1
равно 0, и отрицание этой
1 1 1 0
переменной, если её значение равно 1.
F ( x1 , x 2 , x3 ) x1 x 2 x3 x1 x 2 x 3
x x x x x x x x x
1
2
3
1
2
3
1
2
3
7.
Существование СДНФ позволяет провестипроцедуру, называемую разложением булевой
функции по переменной
x k . Разложение
позволяет представить произвольную функцию
f ( x1 ,..., xn ) в виде
f ( x1 ,..., xn ) xk p( x1 ,..., xk 1 , xk 1 ,..., xn ) x k q( x1 ,..., xk 1 , xk 1 ,..., xn )
p и q – функции, не зависящие от
xk .
F ( x1 , x2 , x3 ) x1 x2 x1 x2 x 3
Пример.
Функция разложена по переменной x1 .
q( x2 ) x2
p( x2 , x3 ) x2 x 3
8.
Задача. По заданной таблице истинностинайти логическую функцию.
х1 х2 х3 F
Решение. Составим СДНФ:
F ( x1 , x2 , x3 ) x1 x 2 x 3 x1 x 2 x3 x1 x2 x 3 x1 x 2 x3 . 0 0 0 1
Минимизируем полученную
0 0 1 1
функцию, предварительно
0 1 0 1
разложив её по переменной x3 : 0 1 1 0
x3 x1 x 2 x1 x 2 x 3 x1 x 2 x1 x2 x 2 x3 x1 x 3 . 1 0 0 0
Здесь был применён закон
1 0 1 1
алгебры логики – закон
1 1 0 0
склеивания: ab ab a .
1 1 1 0
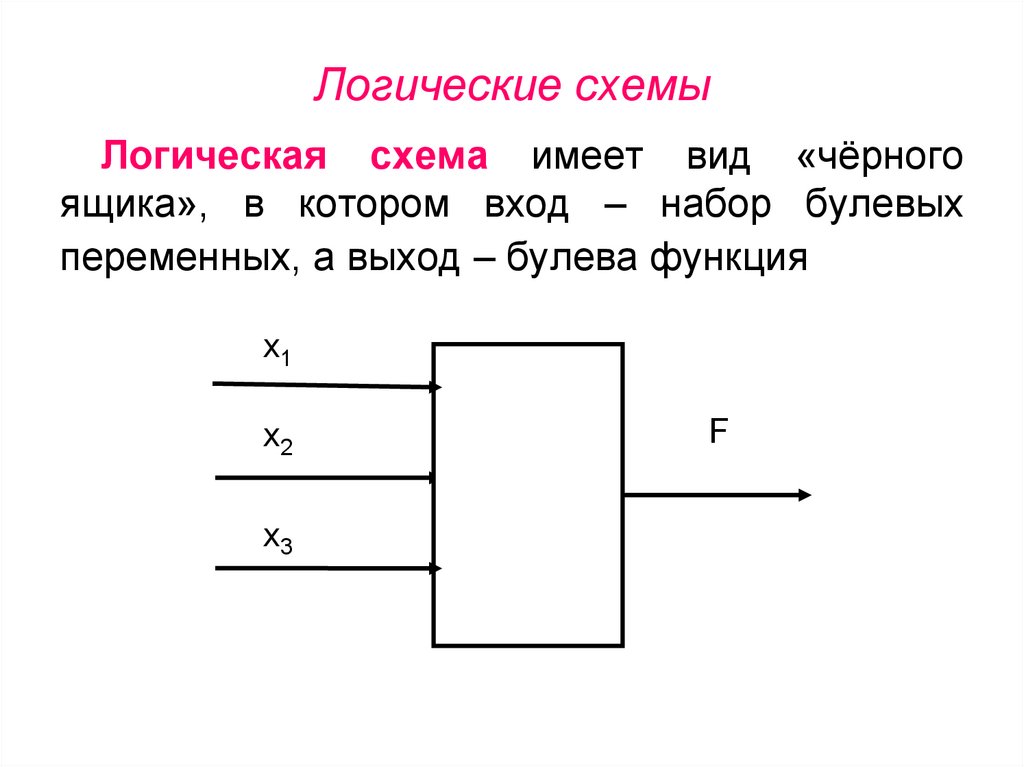
9. Логические схемы
Логическая схема имеет вид «чёрногоящика», в котором вход – набор булевых
переменных, а выход – булева функция
х1
х2
х3
F
10.
Задача.По заданной таблице истинности
построить логическую схему.
х1 х2 х3 F
Решение.
0 0 0 0
F ( x1 , x2 , x3 ) x1 x 2 x3 x1 x2 x 3 x1 x2 x3 .
0 0 1 0
Минимизируем результат:
0 1 0 0
x 2 x1 x3 x 2 x1 x 3 x1 x3 x1 x 2 x3 x1 x 2
0 1 1 0
x1 x 2 x 2 x3 x1 x 2 x3 x1 x 2 x1 x3
1 0 0 0
1 0 1 1
Для минимизации применили
разложение по x 2 , законы
1 1 0 1
склеивания,
переместительный, 1 1 1 1
распределительный и Порецкого.
11.
Построим два варианта логических схем побулеву выражению: а) F ( x1 , x2 , x3 ) x1 x3 x2
х1
х2
И
ИЛИ
х3
б)
F ( x1 , x2 , x3 ) x1 x3 x1 x2 .
х1
И
ИЛИ
х2
х3
И
б
12. Карты Карно
Карты Карно являются одним из наиболееудобных
способов
минимизации.
Это
специальные таблицы, дающие возможность
упростить процесс поиска минимальной формы
булева выражения с помощью графического
представления для количества переменных
n≤6.
Они
имеют
вид
прямоугольника,
разделённого на 2n клеток, в каждой из которых
– двоичный n-мерный набор значений функции
F
из
таблицы
истинности.
Отрицанию
переменной соответствует значение 0, самой
переменной – значение 1.
13.
Логическая функция F на карте представленасовокупностью клеток, заполненных единицами
или нулями, если известны её значения при
всём наборе аргументов, т.е. известна таблица
истинности или СДНФ.
Для
построения
минимальной
ДНФ
производится
«склеивание»
единиц.
Склеиваются только соседние клетки, которые
отличаются значением одной переменной.
Процесс сводится к объединению в группы
единичных клеток карт Карно. При этом общие
переменные
сохраняются,
а
различные
опускаются.
14. Алгоритм «склеивания»
1. Привести булеву функцию к ДНФ.2. Нанести единицы на карту Карно.
3. Объединить соседние единицы контурами,
охватывающими 2т клеток, где т=0, 1, 2, 3.
При этом может оказаться, что единица
попадает одновременно в два контура.
Контуры следует делать по возможности
крупнее.
4. Провести упрощения, т.е. в каждом контуре
оставить
только
общие
переменные,
объединённые конъюнкцией.
5. Объединить конъюнкции дизъюнкциями.
15.
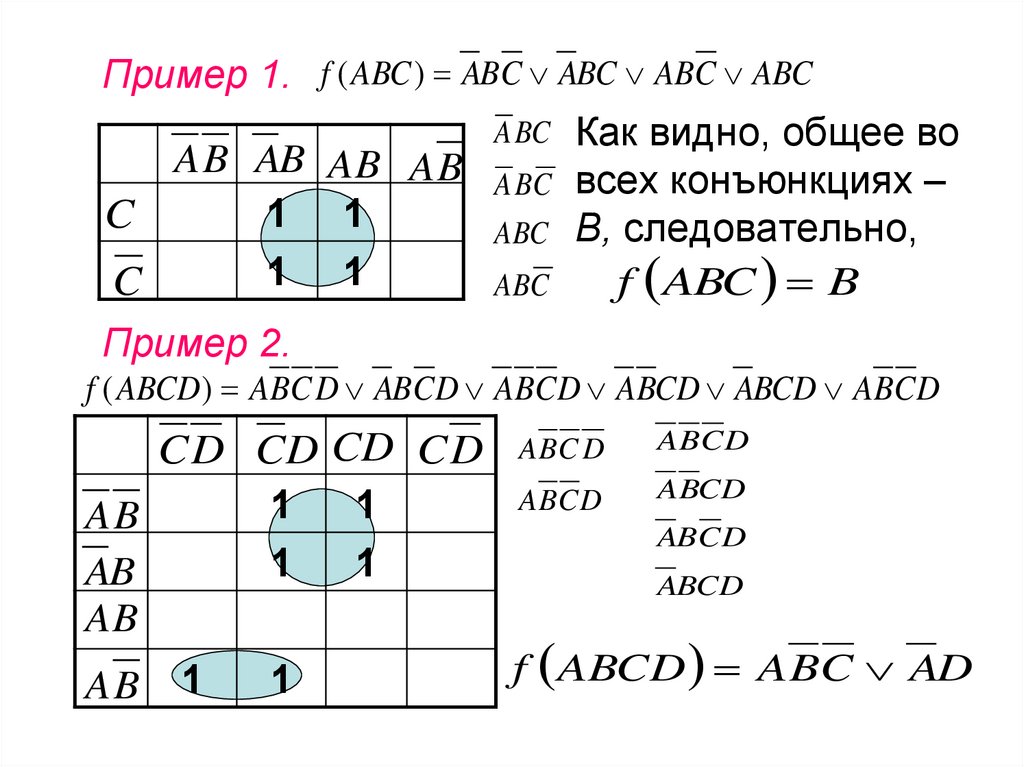
Пример 1. f ( ABC ) ABC ABC ABC ABCA BC Как видно, общее во
A B AB AB A B
A BC всех конъюнкциях –
1 1
C
ABC В, следовательно,
1 1
f ABC B
C
ABC
Пример 2.
f ( ABCD ) ABC D ABCD ABCD ABCD ABCD ABCD
C D CD CD C D
1
1
AB
AB
AB
AB
1
1
1
1
A BC D
A BC D
A BC D
A BCD
ABC D
ABCD
f ABCD A BC AD
16.
Карту можно сворачивать в вертикальныйцилиндр, т.е. «склеивать» её вертикальные
края. При этом совмещении единицы первого и
последнего столбцов окажутся соседними и
для них можно будет применить алгоритм
склеивания.
Карту можно сворачивать в горизонтальный
цилиндр, т.е. «склеивать» её горизонтальные
края. При этом единицы верхней и нижней
строк окажутся соседними.
Карту можно свернуть в шар и одновременно
«склеить» четыре единицы, расположенные в
углах.
17.
C D CD CD C DAB
AB 1
AB 1
AB
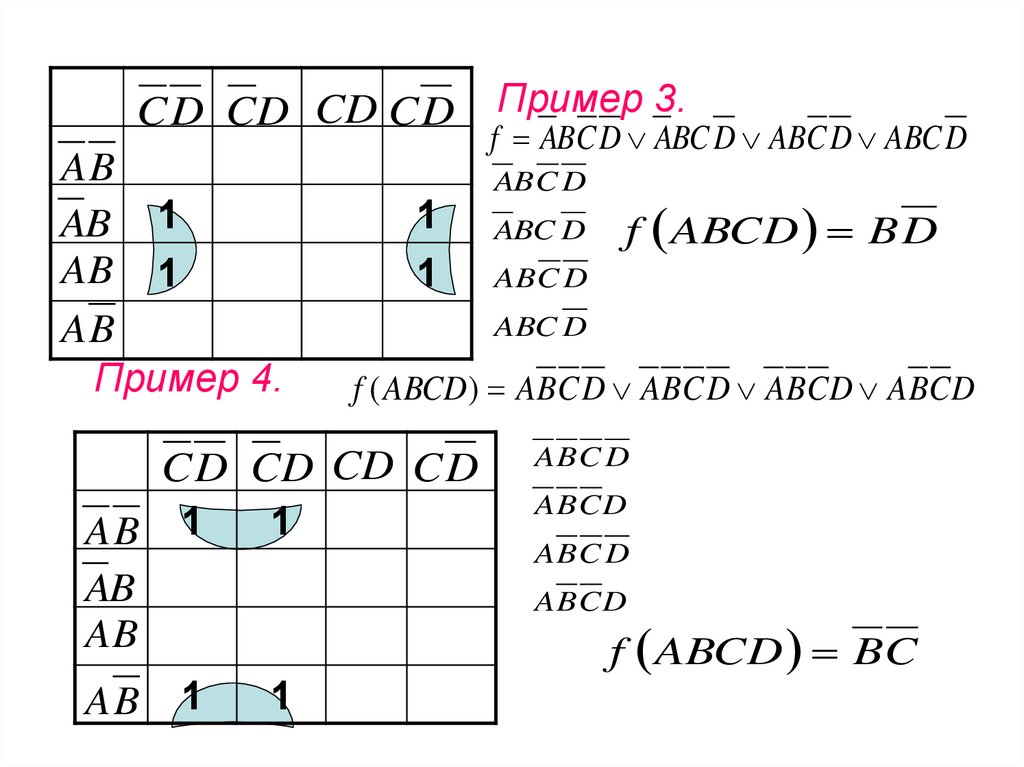
Пример 4.
AB
AB
AB
AB
1
1
f ABC D ABC D ABC D ABC D
AB C D
1
1
ABC D
f ABCD B D
ABC D
ABC D
f ( ABCD ) ABC D ABC D ABCD ABCD
C D CD CD C D
1
Пример 3.
A BC D
A BC D
A BC D
A BC D
f ABCD BC
1
18.
C D CD CD C DAB
1
1
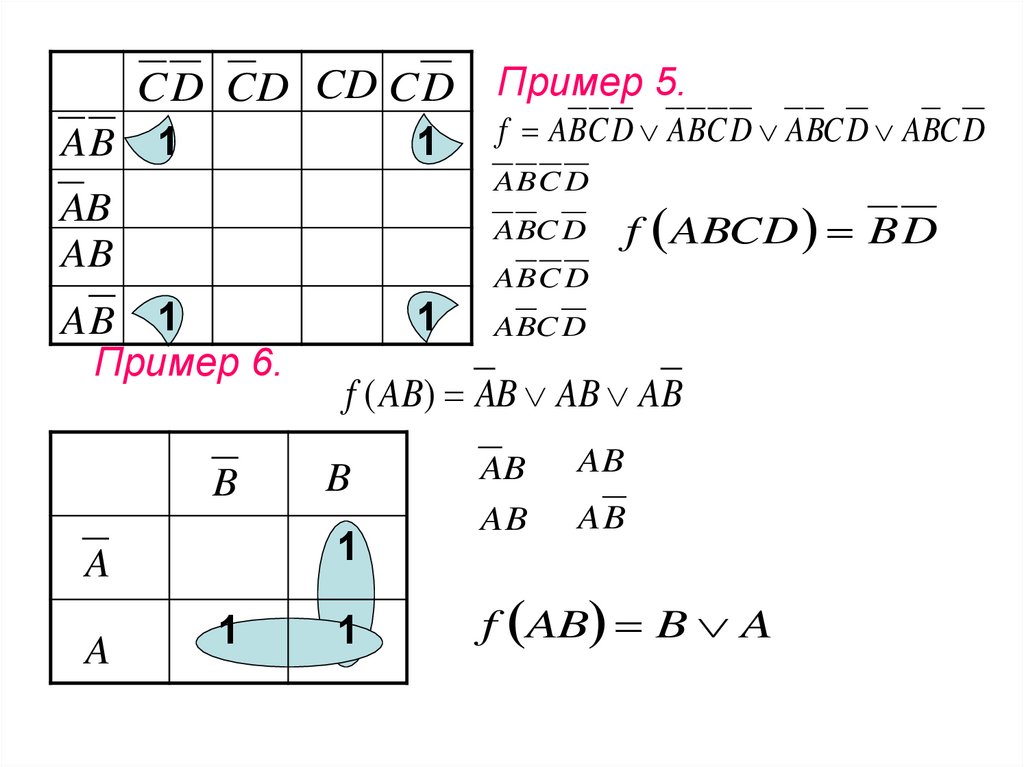
f ABC D ABC D ABC D ABC D
A BC D
AB
AB
A BC D
f ABCD B D
A BC D
AB 1
Пример 6.
B
1
1
A BC D
f ( AB) AB AB AB
B
1
A
A
Пример 5.
1
AB
AB
AB
AB
f AB B A
19. 2.5. Полином Жегалкина
В СДНФ булевой функции только одна изэлементарных конъюнкций равна 1. Это даёт
основание представить любую булеву функцию
с помощью операции сложения по модулю два.
Заменив в СДНФ x i на 1 xi x i и используя
распределительный закон для конъюнкции
относительно сложения по модулю два, имеем
1 xi 1 x j 1 xi x j xi x j . Тогда, учитывая,
что f f 0 , а f 0 f ,
булеву
функцию
можно представить в виде суммы по модулю
два конъюнкций.
20.
Пример. Представим в виде полиномаЖегалкина функцию, заданную в виде СДНФ:
f ( x1 x 2 x3 ) x1 x 2 x 3 x1 x 2 x 3
(1 x1 ) x 2 (1 x3 ) x1 (1 x 2 )(1 x3 )
( x 2 x1 x 2 )(1 x3 ) ( x1 x1 x 2 )(1 x3 )
x 2 x 2 x3 x1 x 2 x1 x 2 x3
x1 x1 x3 x1 x 2 x1 x 2 x3
x1 x 2 x1 x3 x 2 x3
















 mathematics
mathematics








