Введение в магнитостатику. Опыт Эрстеда. (Лекция 5)

1.

Кафедра физики
ЛЕКЦИЯ 5.
ПЛАН ЛЕКЦИИ
1. Введение в магнитостатику. Опыт Эрстеда.
2. Индукция магнитного поля .
3. Графическое изображение магнитного поля.
4. Закон Био – Савара - Лапласа.
5. Примеры расчета магнитных полей:
- магнитное поле прямого тока;
- магнитное поле равномерно движущегося заряда
Общая физика. «Магнитостатика»

2.

Кафедра физики
Введение в магнитостатику.
Рене Декарт обнаружил действие
постоянного магнита на железные
опилки (середина 17 века).
I
Эти опыты говорят нам о том,
что вокруг постоянного магнита
и провода с током существует
некая объективная реальность
данная нам в ощущениях и
существующая независимо от
нас – магнитное поле.
Раздел физики, изучающий свойства постоянных магнитных
полей, называется магнитостатикой.
Общая физика. «Магнитостатика»

3.

Кафедра физики
Введение в магнитостатику.
Магнитное поле Земли изучал англичанин Уильям Гильберт
(1564-1603), нам оно нужно для понимания учебного видео.
Общая физика. «Магнитостатика»

4.

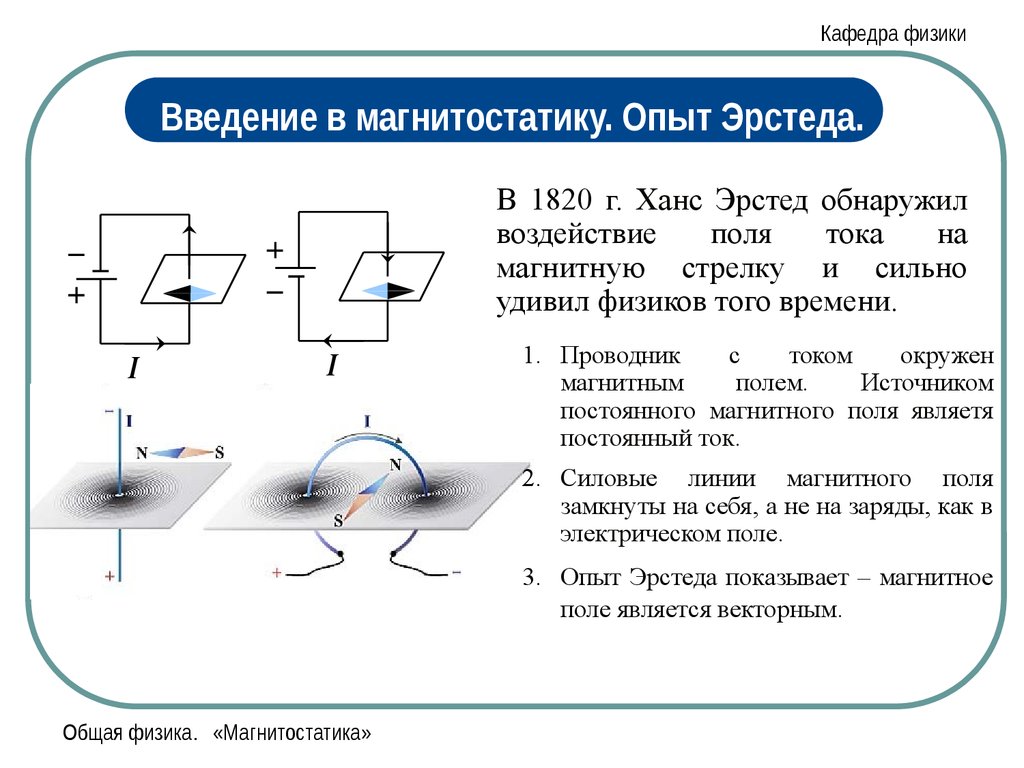
Кафедра физики
Введение в магнитостатику. Опыт Эрстеда.
В 1820 г. Ханс Эрстед обнаружил
воздействие
поля
тока
на
магнитную стрелку и сильно
удивил физиков того времени.
I
I
1. Проводник
с
током
окружен
магнитным
полем.
Источником
постоянного магнитного поля являетя
постоянный ток.
2. Силовые линии магнитного поля
замкнуты на себя, а не на заряды, как в
электрическом поле.
3. Опыт Эрстеда показывает – магнитное
поле является векторным.
Общая физика. «Магнитостатика»

5.

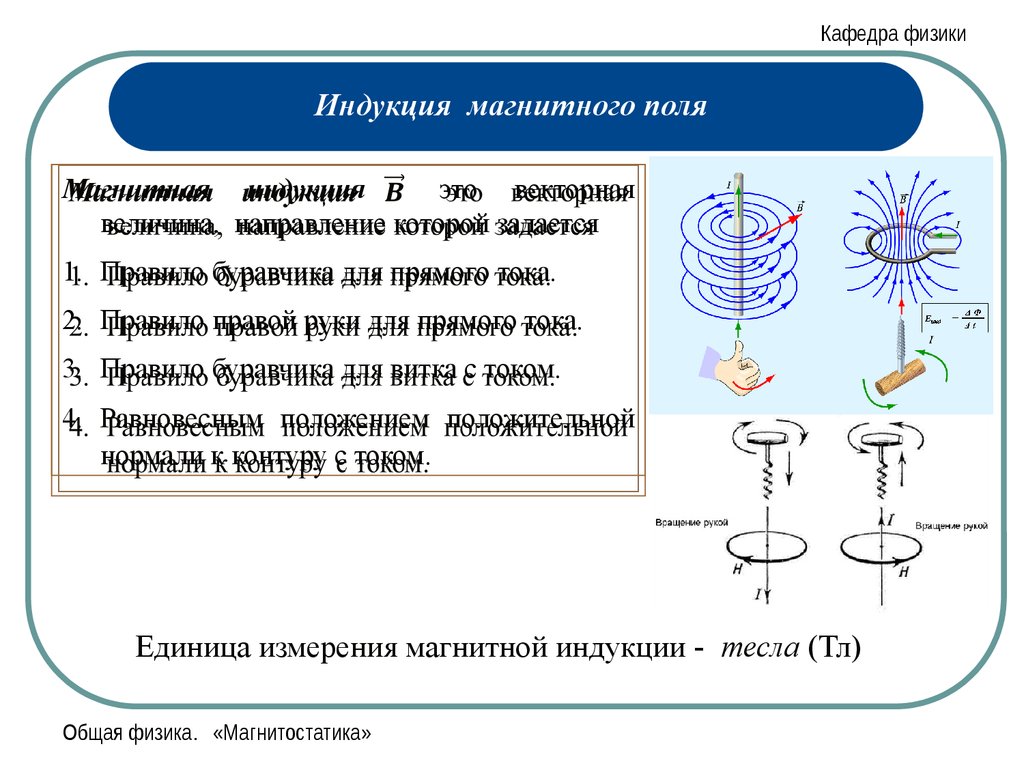
Кафедра физики
Индукция магнитного поля
Магнитная индукция
это векторная
величина, направление которой задается
1. Правило буравчика для прямого тока.
2. Правило правой руки для прямого тока.
3. Правило буравчика для витка с током.
4. Равновесным положением положительной
нормали к контуру с током.
Единица измерения магнитной индукции - тесла (Тл)
Общая физика. «Магнитостатика»

6.

Кафедра физики
Графическое изображение магнитного поля
Как и электрическое поле, магнитное поле изображается с
помощью силовых линий (линий магнитной индукции).
Силовые линии магнитного поля это такие линии, касательные к
которым в каждой точке совпадают по направлению с
векторами магнитной индукции.
Силовые линии любого постоянного магнитного поля являются
замкнутыми, либо начинаются и оканчиваются на бесконечности.
Магнитные поля нужно изображать так, чтобы картина поля давала
кроме направления также представление о величине магнитной
индукции. Для этого в местах увеличения магнитной индукции
силовые линии сгущаются, а в местах ослабления изображаются
более редкими.
Общая физика. «Магнитостатика»

7.

Кафедра физики
Взаимодействие токов. Физический смысл индукции
магнитного поля
Для магнитного поля, как и для электрического,
справедлив принцип суперпозиции:
B,
Поле с магнитной индукцией
порождаемое несколькими
движущимися
зарядами (токами), равно векторной сумме
полей Bi , порождаемых каждым зарядом (током) в
отдельности:
B
Общая физика. «Магнитостатика»
B
i

8.

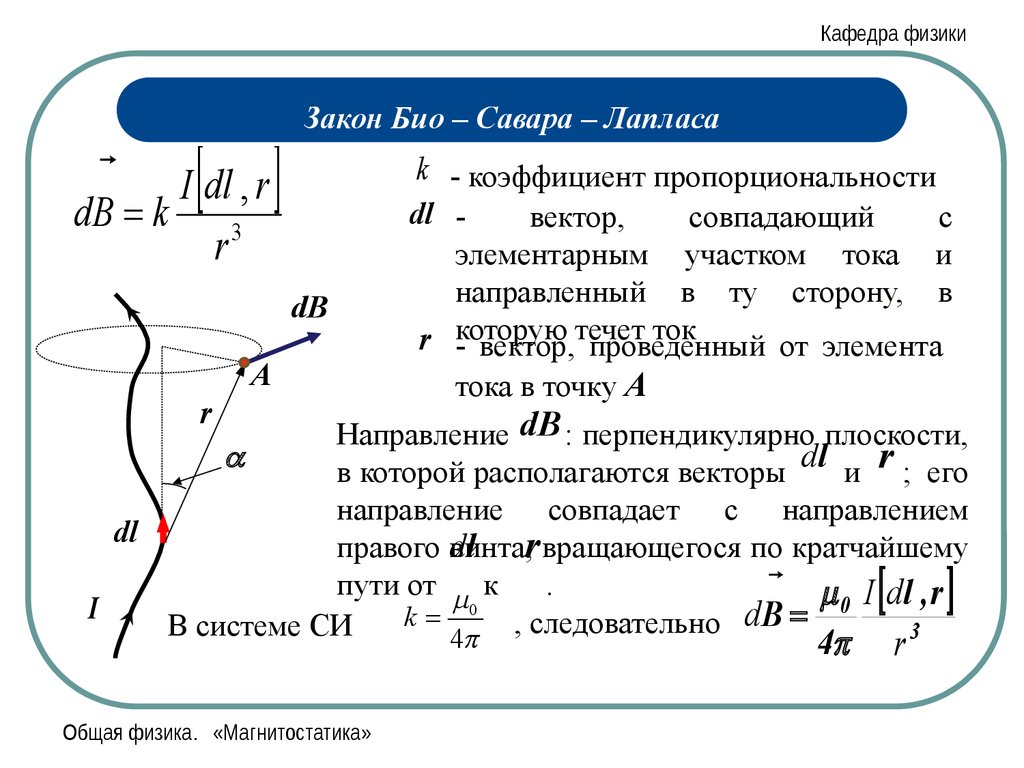
Кафедра физики
Закон Био – Савара – Лапласа
Токи, текущие по проводникам, создают в окружающем
пространстве магнитное поле. Как вычислить магнитное поле
произвольного тока? В электростатике: взаимодействие точечных
зарядов, затем - принцип суперпозиции. В магнитостатике - тот же
прием. Аналог точечных зарядов - малые прямолинейные участки
проводников с током - элементы тока. Важно знать закон, по
которому вычисляется магнитное поле, созданное элементом тока
Для магнитной индукции поля, создаваемого элементом тока
dl , была получена формула
длиной
Это закон Био – Савара – Лапласа
1820 г.
Общая физика. «Магнитостатика»
I dl ,r
dB k 3
r
I

9.

Кафедра физики
I dl , r
dB k 3
r
Закон Био – Савара – Лапласа
k - коэффициент пропорциональности
dl вектор,
совпадающий
с
dB
r
А
элементарным участком тока и
направленный в ту сторону, в
течет ток
r -которую
вектор, проведенный от элемента
тока в точку
А
Направление dB : перпендикулярно плоскости,
в которой располагаются векторы dl и r ; его
направление
совпадает с направлением
dl
dl r вращающегося по кратчайшему
правого винта,
пути от к
.
0 I dl , r
0
I
k
, следовательно dB
В системе СИ
3
4
4
Общая физика. «Магнитостатика»
r

10.

Кафедра физики
Закон Био – Савара – Лапласа
0 I dl , r
dB
4 r 3
Магнитная индукция является силовой
характеристикой магнитного поля.
dB
А
r
dl
I
Модуль dB определяется как
0 I dl r sin 0 I dl sin
dB
3
4
4
r
r2
где - угол между векторами dl и r .
0 - магнитная постоянная
/м[Н/А2]
Общая физика. «Магнитостатика»

11.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Поле прямого тока
I
b
Имеется тонкий, прямой, бесконечно
протяженный проводник, по которому
I
течет ток .
Вычислим магнитную индукцию в
b от
точке А на расстоянии
проводника.
Выделим элементарный участок
тока dl,
радиус-вектор r от элемента
направим
тока dl в точку А.
Общая физика. «Магнитостатика»
А
r
dl

12.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Поле прямого
тока
Элемент тока dl создает в точке А
магнитное поле с индукцией dB .
I
b
Положение dl на рисунке
выбрано
произвольно,
вектор dB от любого
другого dl в точке А будет иметь
dB
одно и то же направление –
перпендикулярно
плоскости
чертежа
Следовательно, сложение векторов dB
можно заменить сложением их модулей.
dl
Общая физика. «Магнитостатика»
dB
А
r

13.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Поле прямого тока
Модуль dB определяется формулой
0 I d l sin
dB
4
r2
Упростим
формулу,
выразив
входящие в нее величины через
один
переменный параметр – угол .
Для этого дополним рисунок и введем
новые обозначения.
I
b
dB
*
dl
r
d
rd
sin
d
d
r*
dl rd / sin
Общая физика. «Магнитостатика»
dB
А
d
r*
r
rd

14.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Поле прямого тока
dB
I
b
dB
А
В итоге получим:
d
r
dl
0 I d l sin
4
r2
rd
bd
b
dl
r
,
2
sin
sin
sin
dB
rd
Общая физика. «Магнитостатика»
0 I b d sin sin 2 0 I sin d
dB
2
2
4
4
b
b sin
Окончательно получили выражение:
0 I
dB
sin d
4 b

15.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Поле прямого тока
0 I
dB
sin d
4 b
Для всех элементов тока угол изменяется в пределах от 0 до .
Проинтегрируем в этих пределах полученное выражение:
0 I
0 I
0 I
B
sin d
( cos ) 0
4 b 0
4 b
2 b
Таким образом, магнитная индукция поля
прямого тока определяется выражением:
Общая физика. «Магнитостатика»
B
0 I
2 b

16.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле равномерно движущегося заряда
Определим величину магнитного поля, создаваемого точечным
зарядом q, движущимся с постоянной нерелятивистской скоростью v
Движущиеся заряды создают ток, поэтому выражение для B, которое
создается движущимся зарядом, получим из формулы
μ0 I dl , r
dB
4π r 3
Пусть имеются носители заряда
упорядоченно со скоростью v .
Общая физика. «Магнитостатика»
e
любого знака, которые движутся

17.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле равномерно движущегося заряда
Эти носители создают ток I j S en v S ,
где S - площадь поперечного сечения проводника,
носителей заряда в единице объема (концентрация).
Преобразуем числитель формулы
0 I dl , r
dB
4 r 3
n - число
I dl , r Idl , r enS dl v , r enSdl v , r
В итоге получим выражение вида
0 enS dl v , r
dB
4
r3
Произведение Sdl это объем отрезка провода длиной dl , поэтому
произведение nSdl равно числу носителей тока в этом объеме
Общая физика. «Магнитостатика»

18.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле равномерно движущегося заряда
0 enS d l v , r
dB
4
r3
nSdl , найдем
Если полученное выражение разделить на
магнитную
индукцию
поля,
создаваемого
одним носителем
e
v
тока , , который
движется со скоростью :
0 e v , r
Установлено, что это выражение справедливо
dB
для любых точечных зарядов,
4 r 3
r размеры
которых много меньше .
Заменив e на
q, окончательно получим
Общая физика. «Магнитостатика»
0 q v , r
B
3
4 r

19.

Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле равномерно движущегося заряда
0 q v , r
B
4 r 3
В полученной формуле r - это радиус-вектор,
проведенный от заряда q к точке
r
наблюдения,
. - его модуль
r
Конец
неподвижен в выбранной системе отсчета, а его начало
движется со скоростью v , поэтому вектор B зависит не только от
положения точки наблюдения, но и от времени.
В соответствии с полученной формулой вектор B располагается
перпендикулярно плоскости, в которой лежат векторы v и r
Общая физика. «Магнитостатика»

20.

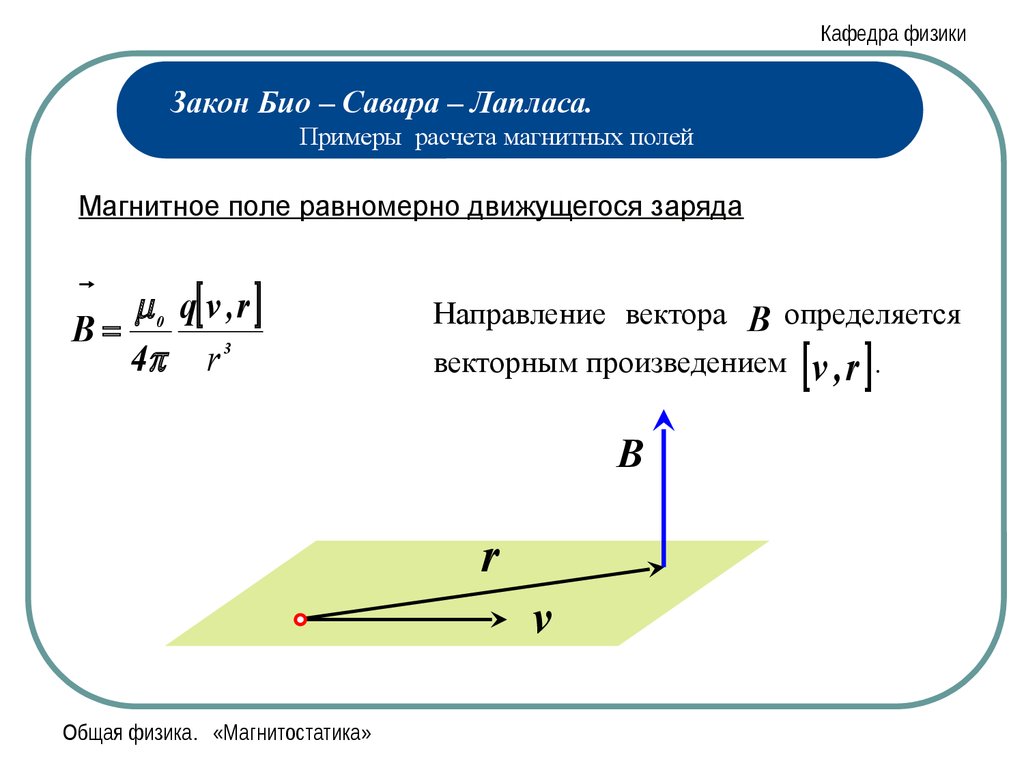
Кафедра физики
Закон Био – Савара – Лапласа.
Примеры расчета магнитных полей
Магнитное поле равномерно движущегося заряда
0 q v , r
B
4 r 3
Направление вектора B определяется
векторным произведением
B
r
Общая физика. «Магнитостатика»
v
.
v ,r

21.

Кафедра физики
Сила Лоренца
Рассмотрим пространство, в котором находятся заряды. Выделим
один из них, обозначим его q. На этот заряд действует сила со
стороны всех остальных зарядов. Эта сила зависит от величин
зарядов, от их взаимного расположения и от того, движутся или
покоятся заряды.
Экспериментами установлено, что на выделенный
заряд в общем случае действует сила:
v - скорость
заряда в рассматриваемой точке пространства
F qE q v , B
B – вектор индукции магнитного поля.
Выражение называется формулой Лоренца, а сила
Лоренца.
Общая физика. «Магнитостатика»
F-
силой

22.

Кафедра физики
Сила Лоренца
В формуле Лоренца
F qE q v , B
Первое слагаемое не зависит от
скорости движения заряда, и
определяет компонент силы,
которая
действует как на
движущийся,
так
и на
неподвижный заряды. E - это
напряженность электрического
поля, т.е. сила, действующая на
неподвижный единичный заряд
со стороны других зарядов
Общая физика. «Магнитостатика»
два слагаемых
Второе слагаемое определяет
компонент
силы,
которая
возникает только тогда, когда
выделенный
заряд
имеет
отличную от нуля скорость.
Вектор B - индукция магнитного
поля. Магнитное поле, в свою
очередь, может быть создано в
пространстве
только
движущимися зарядами.

23.

Кафедра физики
Сила Лоренца
F qE q v , B
v, B
Векторное произведение
Эта сила, как следует
из формулы Лоренца, зависит не только от
модулей векторов B и v, но и от их взаимного
расположения. Если
, тоv , B 0
, даже если
v \\ B
B 0 .
Итак, движущиеся заряды создают в окружающем их пространстве
магнитное поле. Пример движущихся зарядов – протекание тока в
проводниках.
Стационарные
электрические
токи
являются
источниками постоянного магнитного поля. Такое магнитное поле
можно рассматривать отдельно от электрического поля. Раздел
физики - магнитостатика.
Общая физика. «Магнитостатика»