Similar presentations:
Электростатика. Потенциал электростатического поля. Напряжение. (Лекция 2.2)
1.
Кафедра физикиЛекция 2_2
ЭЛЕКТРОСТАТИКА
ПЛАН ЛЕКЦИИ
1. Потенциал электростатического поля. Напряжение.
2. Электродвижущая сила.
3. Вычисление потенциалов электростатических полей :
- Потенциал поля бесконечной заряженной плоскости
- Потенциал поля двух разноименно заряженных плоскостей
- Потенциал поля бесконечного заряженного цилиндра
- Потенциал поля объемно-заряженного шара
Общая физика. «Электростатика»
2.
ПОТЕНЦИАЛЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
F
E
- напряженность
qпр
Wp
- потенциал
qпр
Кафедра физики
основные характеристики
электростатического поля
Напряженность - силовая характеристика поля
Потенциал - это энергетическая характеристика поля, т.к. он
определяет потенциальную энергию зарядов по отношению к полю.
Связь между напряженностью и потенциалом выражается формулой
E qrad
ex
ey
e z
y
z
x
Общая физика. «Электростатика»
3.
ПОТЕНЦИАЛЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Электростатическое поле является одномерным, если
характеристики поля зависят лишь от одной координаты.
Поля сферической, цилиндрической и плоской симметрий –
одномерные поля. В полях сферической и цилиндрической
симметрий характеристики зависят от радиальной координаты r,
центра или оси симметрии. Для этого
которая отсчитывается от
случая формула связи E и выглядит следующим образом:
d 0
E r
r
dr
0
r - единичный вектор, характеризующий направление
Формула используется при расчете электрических полей для
нахождения напряженности E r по известному потенциалу r .
Общая физика. «Электростатика»
4.
ПОТЕНЦИАЛЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Обратная задача – определить связь с E.
В скалярной форме связь и E выглядит как d E r dr.
Тогда
d E r dr
r
r
r
r0
r0
r r0 E r r dr
r
или
Пусть
r0 0
r0
r0
Тогда
r E r r dr
r
Эта формула используется для определения потенциала
известной напряженности E r r .
Общая физика. «Электростатика»
r по
5.
ПОТЕНЦИАЛЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
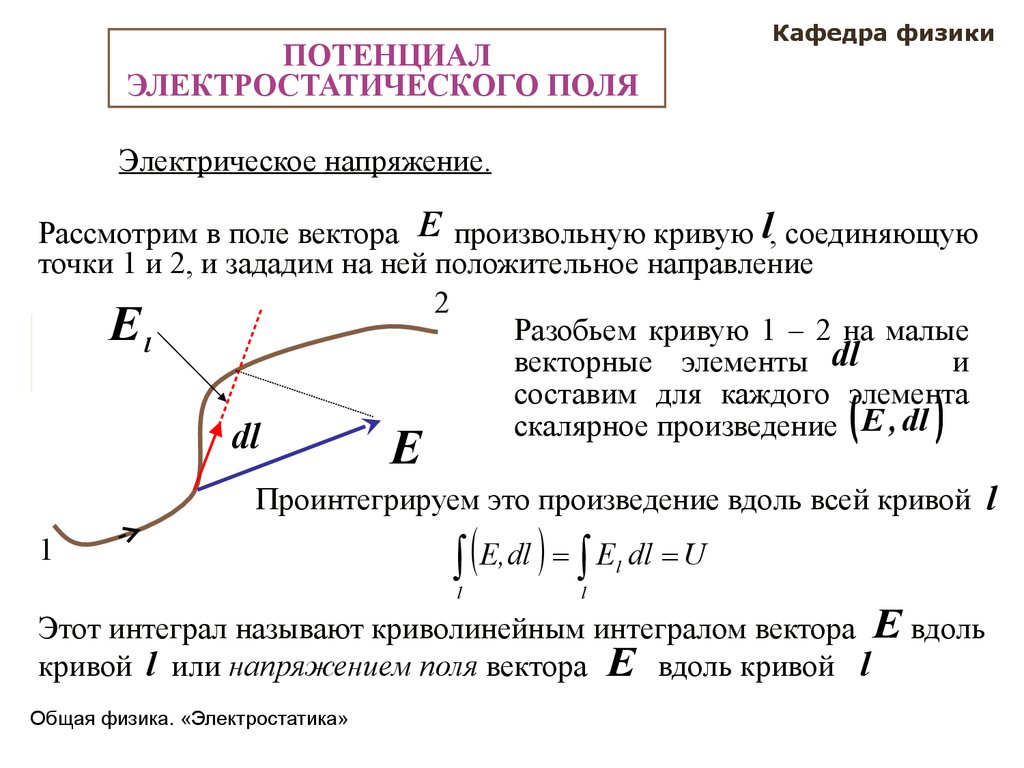
Электрическое напряжение.
Рассмотрим в поле вектора E произвольную кривую l, соединяющую
точки 1 и 2, и зададим на ней положительное направление
2
малые
Разобьем кривую 1 – 2 на
El
векторные элементы dl
и
составим для каждого элемента
скалярное произведение E , dl
dl
E
1
Проинтегрируем это произведение вдоль всей кривой l
E,dl El dl U
l
l
Этот интеграл называют криволинейным интегралом
вектора
кривой l или напряжением поля вектора E вдоль кривой l
Общая физика. «Электростатика»
E вдоль
6.
Кафедра физикиПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Электрическое напряжение.
2
El
2
dl
1
E
l
E,dl El dl U
l
Напряжение поля вектора E вдоль кривой l
показывает, в какой мере вектор E
dl кривой l.
проецируется на элементы
Поскольку вектор E
имеет смысл силы,
действующей на единичный положительный
заряд, то интеграл выражает работу поля по перемещению
такого заряда вдоль кривой l.
Работа сил поля над зарядом q равна произведению величины заряда
на разность потенциалов в начальной и конечной точках: A12 q 1 2
1
Тогда, обозначив точки 1, 2 на кривой 1 и 2 , для единичного
положительного заряда можно записать интеграл в виде
U
Общая физика. «Электростатика»
l
E, dl 1 2
7.
Кафедра физикиПОТЕНЦИАЛ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
U 1 2 Отсюда следует, что
Электрическое напряжение.
Электрическое напряжение вдоль кривой не зависит от
формы кривой и определяется только положениями
начальной и конечной точек
2
l 21
Если кривая замкнутая, то интеграл, имеет
название – циркуляция векторного поля
(циркуляция вектора напряженности) по
контуру
Рассмотрим замкнутый контур L l12 l 21
2
l12
1
1
L
Запишем для контура L
E, dl E, dl E, dl ( 1 2 ) ( 2 1 ) 0
Общая физика. «Электростатика»
l12
l21
8.
ПОТЕНЦИАЛЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Кафедра физики
Электрическое напряжение.
Запишем определение:
Циркуляция вектора напряженности электростатического поля по
контуру называется электродвижущей силой это контура (ЭДС)
Исходя из этого определения, полученное соотношение для замкнутого
контура
E , dl 0
L
можно сформулировать в виде нового определения
В электростатическом поле ЭДС замкнутого контура равна нулю
Общая физика. «Электростатика»
9.
Кафедра физикиРасчет потенциалов электростатических полей.
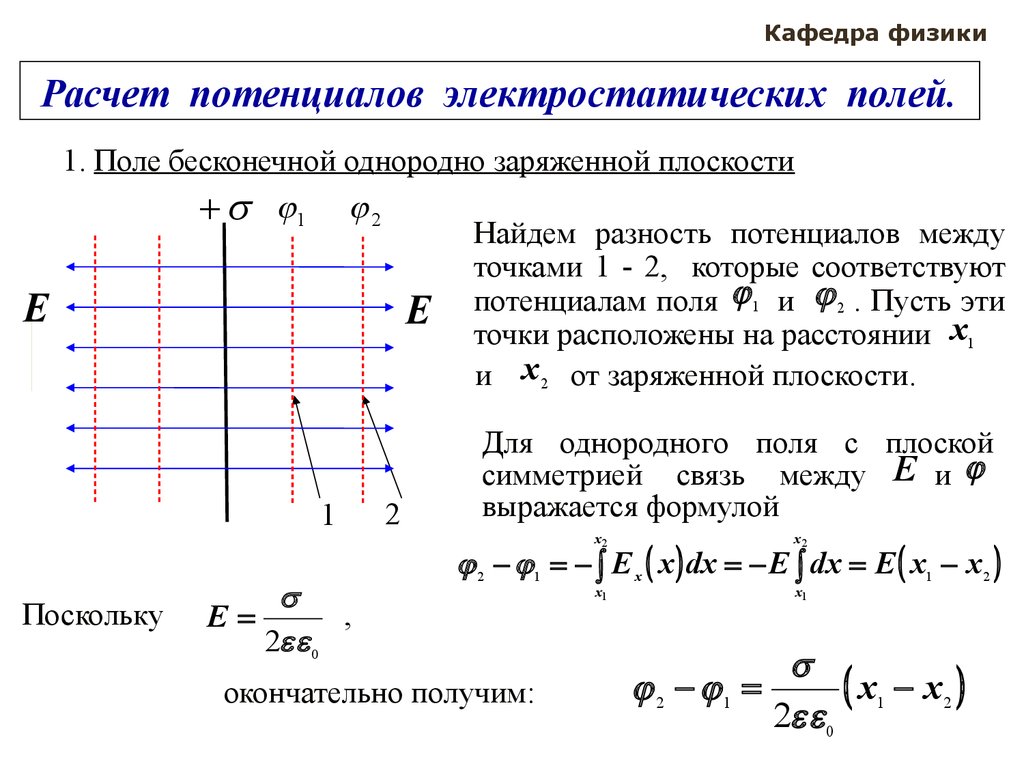
1. Поле бесконечной однородно заряженной плоскости
Пусть поверхностная плотность положительного заряда во всех
точках плоскости одинакова и равна
1
E
2
E
Электростатическое поле можно
изобразить графически не только
силовыми линиями, но и с помощью
эквипотенциальных поверхностей.
Эквипотенциальной поверхностью
называется геометрическое место
точек с одинаковым потенциалом.
Эквипотенциальные поверхности поля бесконечной однородно
заряженной плоскости представляют собой плоскости, параллельные
носителю заряда
10.
Кафедра физикиРасчет потенциалов электростатических полей.
1. Поле бесконечной однородно заряженной плоскости
1
2
E
E
1
Поскольку
,
E
2 0
2
Найдем разность потенциалов между
точками 1 - 2, которые соответствуют
потенциалам поля 1 и 2 . Пусть эти
точки расположены на расстоянии x1
и. x 2 от заряженной плоскости.
Для однородного поля с плоской
симметрией связь между E и .
выражается формулой
x2
x2
x1
x1
2 1 E x x dx E dx E x1 x 2
окончательно получим:
x1 x2
2 1
2 0
11.
Кафедра физикиРасчет потенциалов электростатических полей.
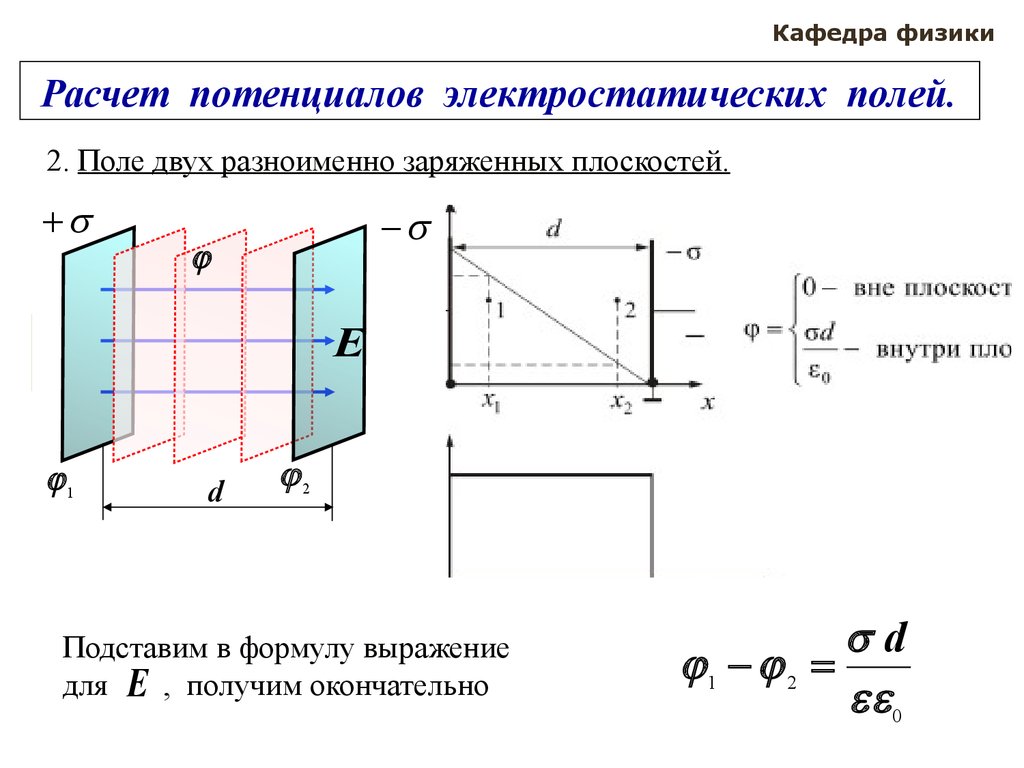
2. Поле двух разноименно заряженных плоскостей.
E
1
d
2
Две параллельные бесконечные плоскости
заряжены разноименно с одинаковой по
величине поверхностной плотностью
Поле сосредоточено между плоскостями и
однородно. В области между плоскостями
E
0
Вне плоскостей
Формула связи между
После интегрирования получим
Подставим в формулу выражение
для E , получим окончательно
иE
:
E 0
d Edx
d
d
0
0
1 2 Edx E dx Ed
d
1 2
0
12.
Кафедра физикиРасчет потенциалов электростатических полей.
2. Поле двух разноименно заряженных плоскостей.
E
1
d
2
Подставим в формулу выражение
для E , получим окончательно
d
1 2
0
13.
Кафедра физикиРасчет потенциалов электростатических полей.
3. Поле бесконечного заряженного цилиндра
Поле создается бесконечной положительно
заряженной цилиндрической поверхностью
Напряженность поля в каждой точке
направлена
вдоль
радиальной
прямой,
перпендикулярной к оси цилиндра
Определим разность потенциалов между
точками r1 и r2 .
1
E r
2 0 r
r R
r dr
r2
1 2 E r dr
ln
r
2 0 r r 2 0 r1
r2
2
1
1
r2
1 2
ln
2 0 r1
E
E
1
2
r1
r2
14.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
Рассмотрим область пространства, представляющую собой шар
радиусом R с объемной плотностью заряда .
Найдем потенциал электрического поля
внутри и вне шара.
0 r R
- поле внутри шара
R
1
q
E r
r
3
4 0 R
q
4 0 r
3 0
r R
- поле вне шара
E r
E r
r
2
E r
R3
3 0 r 2
15.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
Определим r по известной величине E r . Уравнение связи для
одномерного поля со сферической симметрией выглядит так:
r
R
r0
r E r r dr
r
Интегрирование проведем по радиальной
прямой r, соединяющей центр шара с точкой,
удаленной в бесконечность
- поле внутри шара 0 r R
Для определения r внутри шара интегрирование
проведем через две области с разными формулами
напряженности.
16.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R 3 dr
r
rdr
2
3 0 r
3 0 R r
R
R
Вычислим интегралы:
R
dr
3
r
( rdr R 2 )
3εε0
r
R
r
ρ
Первый интеграл:
R
1 2 2
rdr R r
2
r
Второй интеграл:
dr
1
3 1
3 1
R
R R
R2
2
R
r R
r
R
3
17.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
В итоге получим
r
1 2
2 R 2 ρ 3 R 2 1 r 2 ρ 3 R 2 1 r 2
R
r
3εε
3εε0 2
2 3εε0 2
3
0 2
ρ
Окончательно
2 1 2
r
R r
2εε0
3
ρ
18.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
- поле вне шара
r R
Для внешней области интегрируем по той же линии
от r r R до .
r Er r dr
r
ρ R3
dr
3εε0 r r 2
Такой интеграл мы рассмотрели выше -
В итоге для внешней области шара получим
r
dr
1
r2 r
r
ρ R3
3εε0 r
19.
Кафедра физикиРасчет потенциалов электростатических полей.
4. Поле объемно-заряженного шара
r
R
Таким образом, потенциал поля
объемнозаряженного шара определяется выражениями:
ρ R3
r
0 r R
3εε0 r
r
2 1 2
R r
2εε0
3
ρ
r R
Проверим правильность выражений
При r R потенциал должен быть одинаковым независимо от формулы.
2 1 2
ρ
R
R2
R R
2εε0
3
3εε0
ρ
R
ρ R3
3εε0 R
ρ
3εε0
R2
















 physics
physics








