Similar presentations:
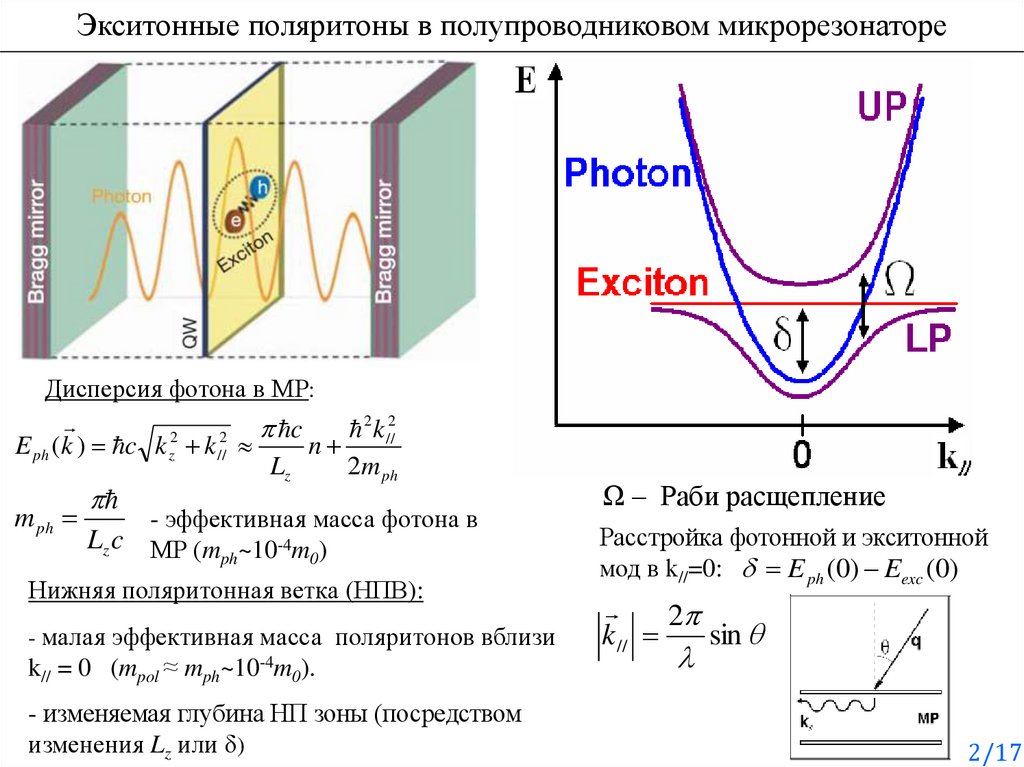
Экситонные поляритоны в полупроводниковом микрорезонаторе
1. Loss of coherence in cavity-polariton condensates: Effect of disorder versus exciton reservoir
A. A. Demenev, Ya. V. Grishina, S. I. Novikov, V. D. Kulakovskii, C.Schneider, S. Höfling
Phys. Rev. B. 94, 195302 (2016).
Polarization instability and the nonlinear internal
Josephson effect in cavity polariton condensates
generated in an excited state in GaAs microcavities
of lowered symmetry
A. A. Demenev, Ya. V. Grishina, A. V. Larionov, N. A. Gippius, C.
Schneider, S. Höfling, V. D. Kulakovskii
Phys. Rev. B 96, 155308 (2017).
2. Экситонные поляритоны в полупроводниковом микрорезонаторе
Дисперсия фотона в МР:2 k //2
c
2
2
E ph (k ) c k z k //
n
Lz
2m ph
m ph
Lz c
- эффективная масса фотона в
МР (mph~10-4m0)
Нижняя поляритонная ветка (НПВ):
- малая эффективная масса поляритонов вблизи
k// = 0 (mpol ≈ mph~10-4m0).
- изменяемая глубина НП зоны (посредством
изменения Lz или δ)
Ω – Раби расщепление
Расстройка фотонной и экситонной
мод в k//=0: E ph (0) Eexc (0)
2
k //
sin
2/17
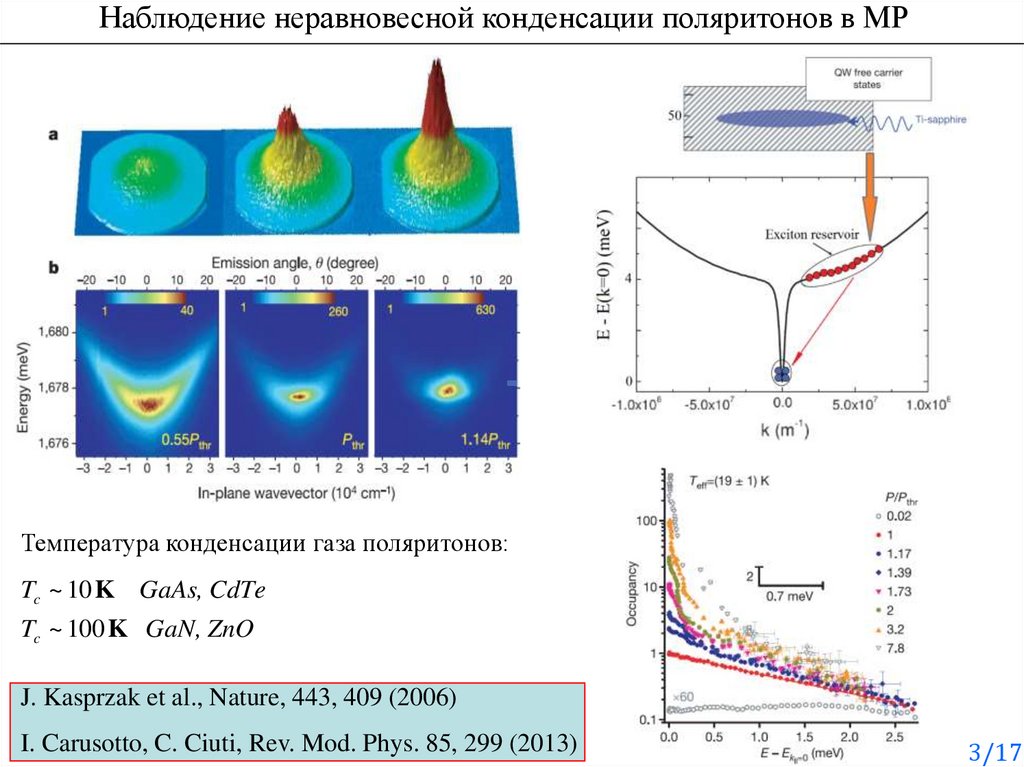
3.
Наблюдение неравновесной конденсации поляритонов в МРТемпература конденсации газа поляритонов:
Tc ~ 10 K GaAs, CdTe
Tc ~ 100 K GaN, ZnO
J. Kasprzak et al., Nature, 443, 409 (2006)
I. Carusotto, C. Ciuti, Rev. Mod. Phys. 85, 299 (2013)
3/17
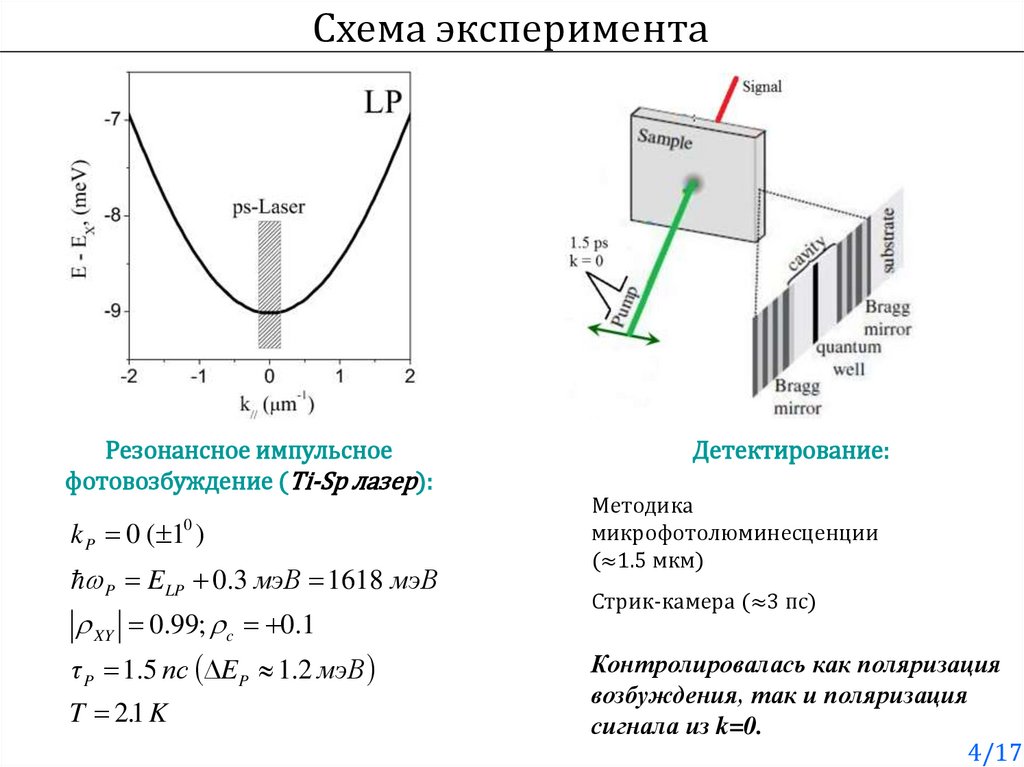
4.
Схема экспериментаРезонансное импульсное
фотовозбуждение (Ti-Sp лазер):
k P 0 ( 1 )
0
P E LP 0.3 мэВ 1618 мэВ
XY 0.99; c 0.1
τ P 1.5 пс E P 1.2 мэВ
T 2.1 K
Детектирование:
Методика
микрофотолюминесценции
(≈1.5 мкм)
Стрик-камера (≈3 пс)
Контролировалась как поляризация
возбуждения, так и поляризация
сигнала из k=0.
4/17
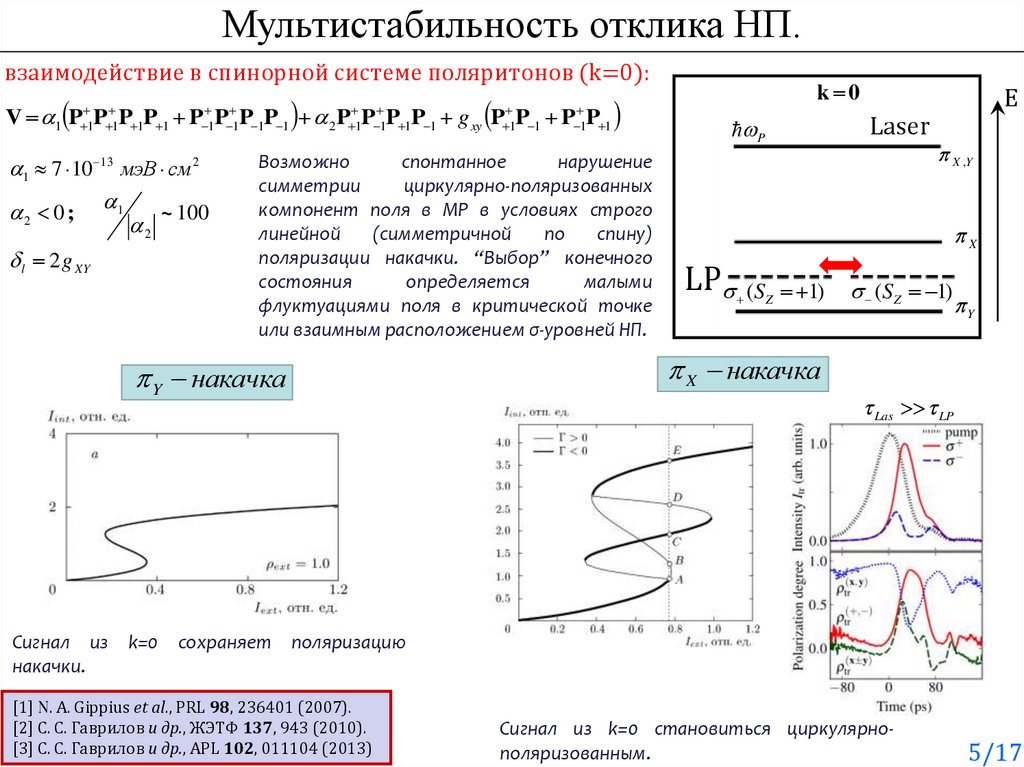
5.
Мультистабильность отклика НП.взаимодействие в спинорной системе поляритонов (k=0):
V 1 P P P P P P P P P P P P g xy P P P P
1 1 1 1
1 1 1 1
1 7 10 13 мэВ см 2
2 0 ; 1
~ 100
2
l 2 g XY
2 1 1 1 1
1 1
1 1
Возможно
спонтанное
нарушение
симметрии
циркулярно-поляризованных
компонент поля в МР в условиях строго
линейной
(симметричной
по
спину)
поляризации накачки. “Выбор” конечного
состояния
определяется
малыми
флуктуациями поля в критической точке
или взаимным расположением σ-уровней НП.
Y накачка
k 0
P
E
Laser
X ,Y
X
LP
(SZ 1)
(SZ 1)
Y
X накачка
Las LP
Сигнал из k=0 сохраняет поляризацию
накачки.
[1] N. A. Gippius et al., PRL 98, 236401 (2007).
[2] С. С. Гаврилов и др., ЖЭТФ 137, 943 (2010).
[3] С. С. Гаврилов и др., APL 102, 011104 (2013)
Сигнал из k=0 становиться циркулярнополяризованным.
5/17
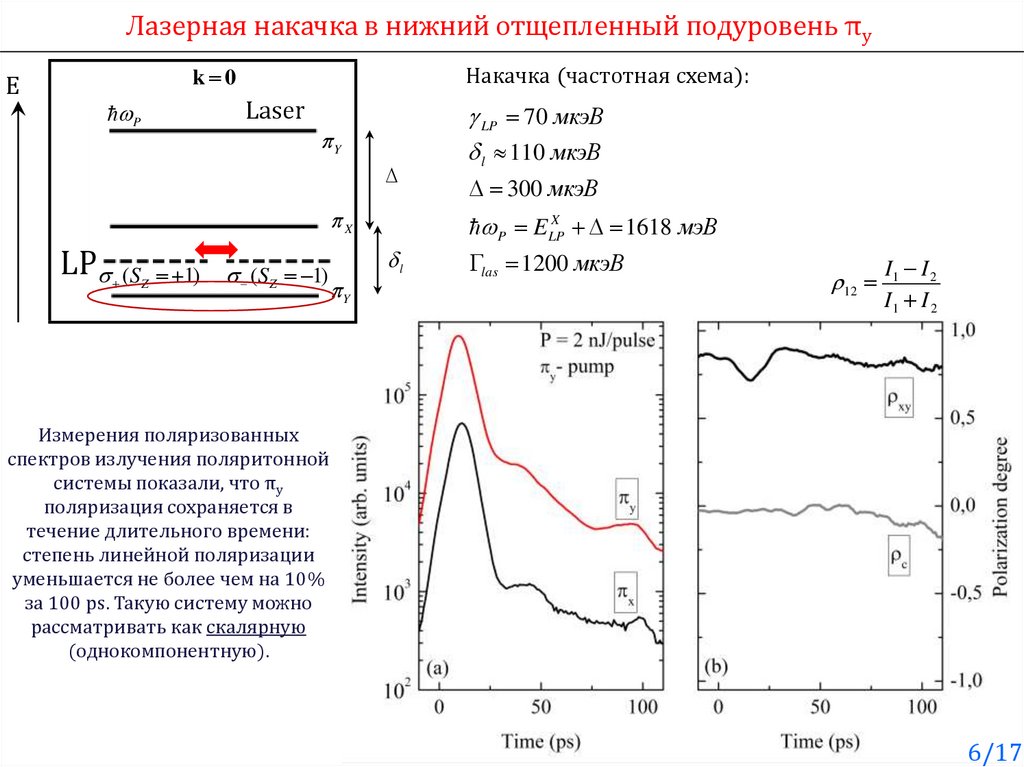
6.
Лазерная накачка в нижний отщепленный подуровень πyE
k 0
P
Накачка (частотная схема):
Laser
Y
X
LP
(SZ 1)
(SZ 1)
Y
LP 70 мкэВ
l 110 мкэВ
300 мкэВ
X
P ELP
1618 мэВ
l
las 1200 мкэВ
12
I1 I 2
I1 I 2
Измерения поляризованных
спектров излучения поляритонной
системы показали, что πy
поляризация сохраняется в
течение длительного времени:
степень линейной поляризации
уменьшается не более чем на 10%
за 100 ps. Такую систему можно
рассматривать как скалярную
(однокомпонентную).
6/17
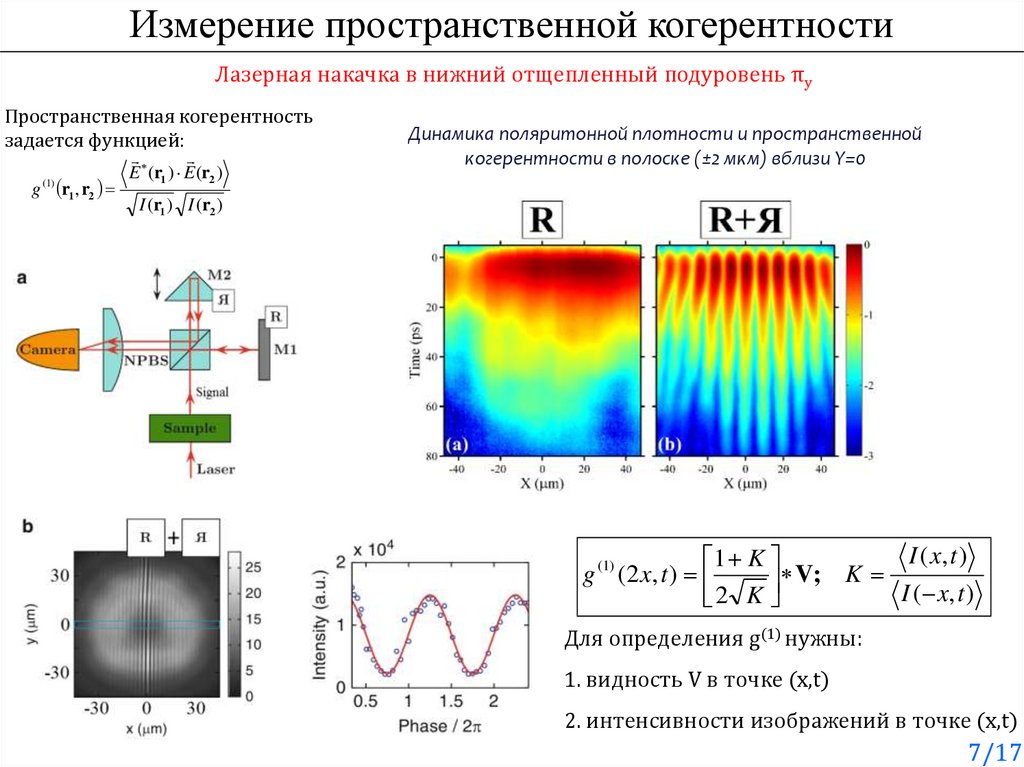
7.
Измерение пространственной когерентностиЛазерная накачка в нижний отщепленный подуровень πy
Пространственная когерентность
задается функцией:
g (1) r1 , r2
E (r1 ) E (r2 )
Динамика поляритонной плотности и пространственной
когерентности в полоске (±2 мкм) вблизи Y=0
I (r1 ) I (r2 )
I ( x, t )
1 K
g (1) (2 x, t )
V;
K
I ( x, t )
2 K
Для определения g(1) нужны:
1. видность V в точке (x,t)
2. интенсивности изображений в точке (x,t)
7/17
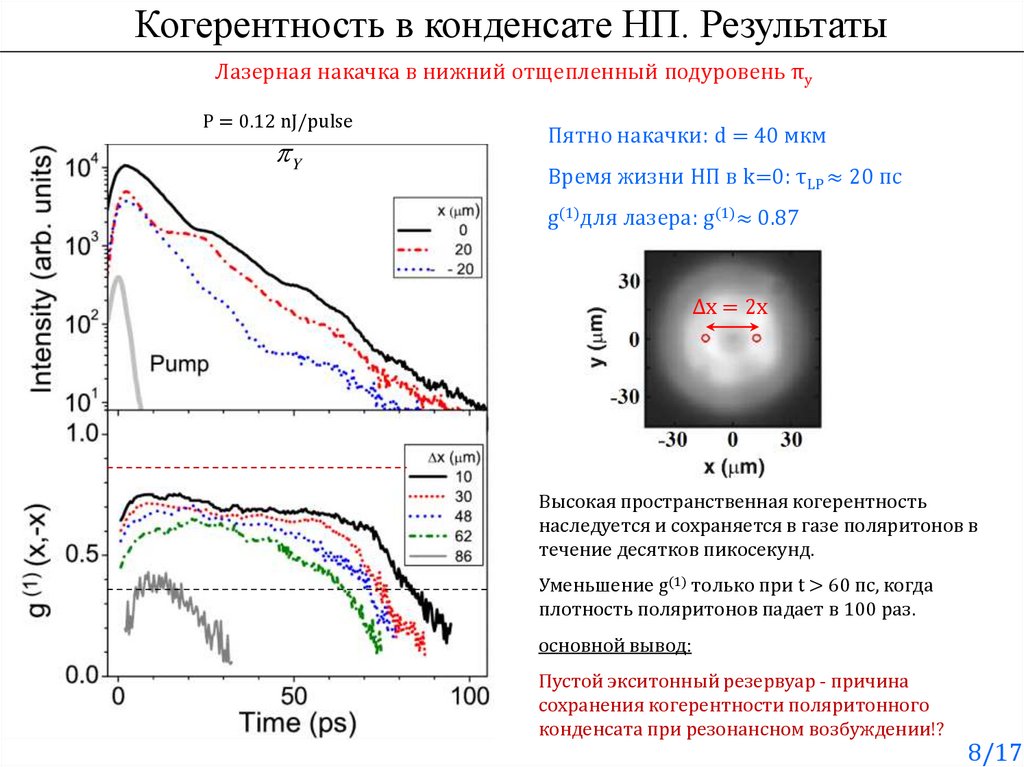
8.
Когерентность в конденсате НП. РезультатыЛазерная накачка в нижний отщепленный подуровень πy
P = 0.12 nJ/pulse
Y
Пятно накачки: d = 40 мкм
Время жизни НП в k=0: τLP ≈ 20 пс
g(1)для лазера: g(1)≈ 0.87
Δx = 2x
Высокая пространственная когерентность
наследуется и сохраняется в газе поляритонов в
течение десятков пикосекунд.
Уменьшение g(1) только при t > 60 пс, когда
плотность поляритонов падает в 100 раз.
основной вывод:
Пустой экситонный резервуар - причина
сохранения когерентности поляритонного
конденсата при резонансном возбуждении!?
8/17
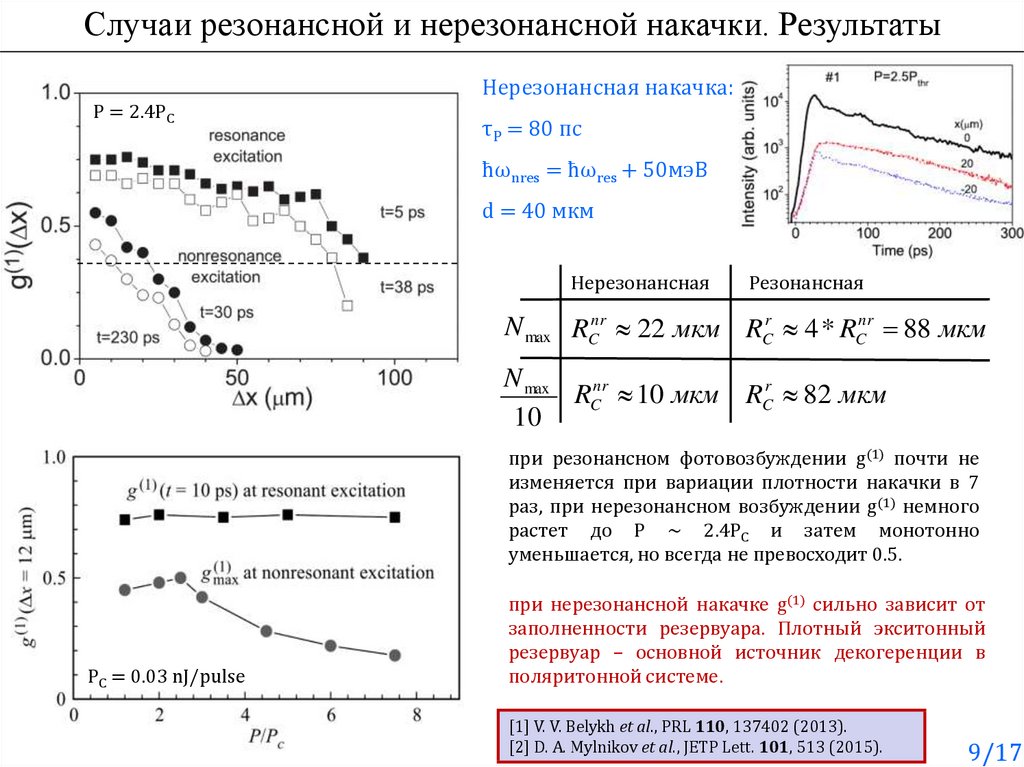
9.
Случаи резонансной и нерезонансной накачки. РезультатыНерезонансная накачка:
P = 2.4PC
τP = 80 пс
ħωnres = ħωres + 50мэВ
d = 40 мкм
Нерезонансная
Резонансная
N max RCnr 22 мкм RCr 4 * RCnr 88 мкм
N max
RCnr 10 мкм RCr 82 мкм
10
при резонансном фотовозбуждении g(1) почти не
изменяется при вариации плотности накачки в 7
раз, при нерезонансном возбуждении g(1) немного
растет до P ∼ 2.4PC и затем монотонно
уменьшается, но всегда не превосходит 0.5.
PC = 0.03 nJ/pulse
при нерезонансной накачке g(1) сильно зависит от
заполненности резервуара. Плотный экситонный
резервуар – основной источник декогеренции в
поляритонной системе.
[1] V. V. Belykh et al., PRL 110, 137402 (2013).
[2] D. A. Mylnikov et al., JETP Lett. 101, 513 (2015).
9/17
10.
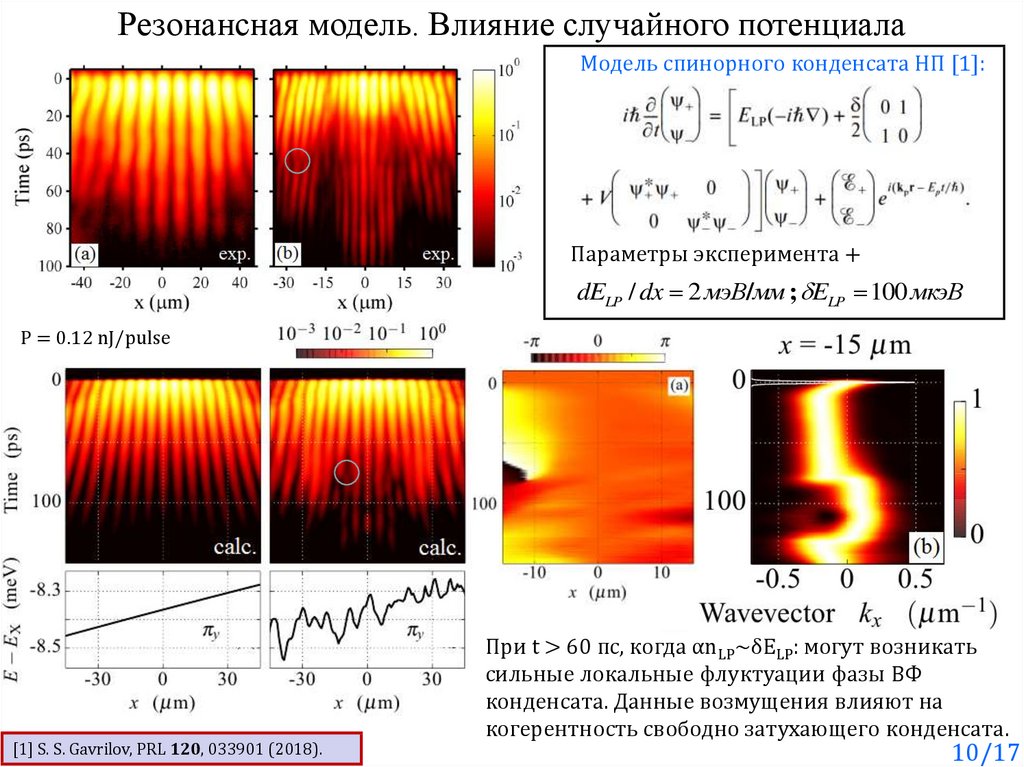
Резонансная модель. Влияние случайного потенциалаМодель спинорного конденсата НП [1]:
Параметры эксперимента +
dELP / dx 2 мэВ/мм ; ELP 100 мкэВ
P = 0.12 nJ/pulse
[1] S. S. Gavrilov, PRL 120, 033901 (2018).
При t > 60 пс, когда αnLP~δELP: могут возникать
сильные локальные флуктуации фазы ВФ
конденсата. Данные возмущения влияют на
когерентность свободно затухающего конденсата.
10/17
11.
Выводы. Накачка в нижний отщепленный подуровень πyПри резонансном возбуждении нижнего отщепленного линейного
подуровня:
-конденсат НП в k=0 сохраняет поляризацию накачки во всей области
времен наблюдения.
-конденсат наследует когерентность лазерного импульса в широком
диапазоне плотностей возбуждения и сохраняет ее в течение
десятков пикосекунд.
Основной причиной нарушения когерентности поляритонного
конденсата при нерезонансном возбуждении является его
взаимодействие с плотным экситонным резервуаром.
-В свободно затухающем поляритонном конденсате, при плотностях
поляритонов, обеспечивающих фиолетовый сдвиг НП меньше
амплитуды случайного потенциала могут возникать сильные
локальные флуктуации фазы ВФ конденсата. Как показывают
расчеты, данные локальные возмущения могут влиять на
корреляционные свойства свободно затухающего конденсата.
11/17
12.
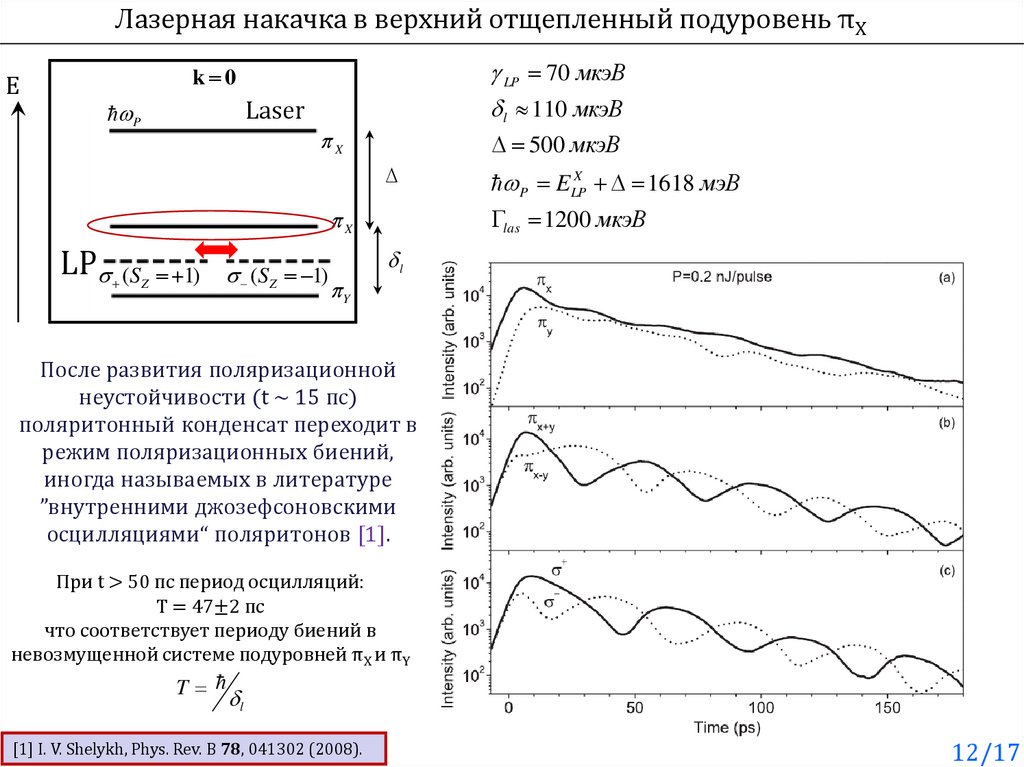
Лазерная накачка в верхний отщепленный подуровень πXE
LP 70 мкэВ
l 110 мкэВ
k 0
P
Laser
X
500 мкэВ
las 1200 мкэВ
X
LP
(SZ 1)
(SZ 1)
Y
X
P ELP
1618 мэВ
l
После развития поляризационной
неустойчивости (t ~ 15 пс)
поляритонный конденсат переходит в
режим поляризационных биений,
иногда называемых в литературе
”внутренними джозефсоновскими
осцилляциями“ поляритонов [1].
При t > 50 пс период осцилляций:
T = 47±2 пс
что соответствует периоду биений в
невозмущенной системе подуровней πX и πY
T
l
[1] I. V. Shelykh, Phys. Rev. B 78, 041302 (2008).
12/17
13.
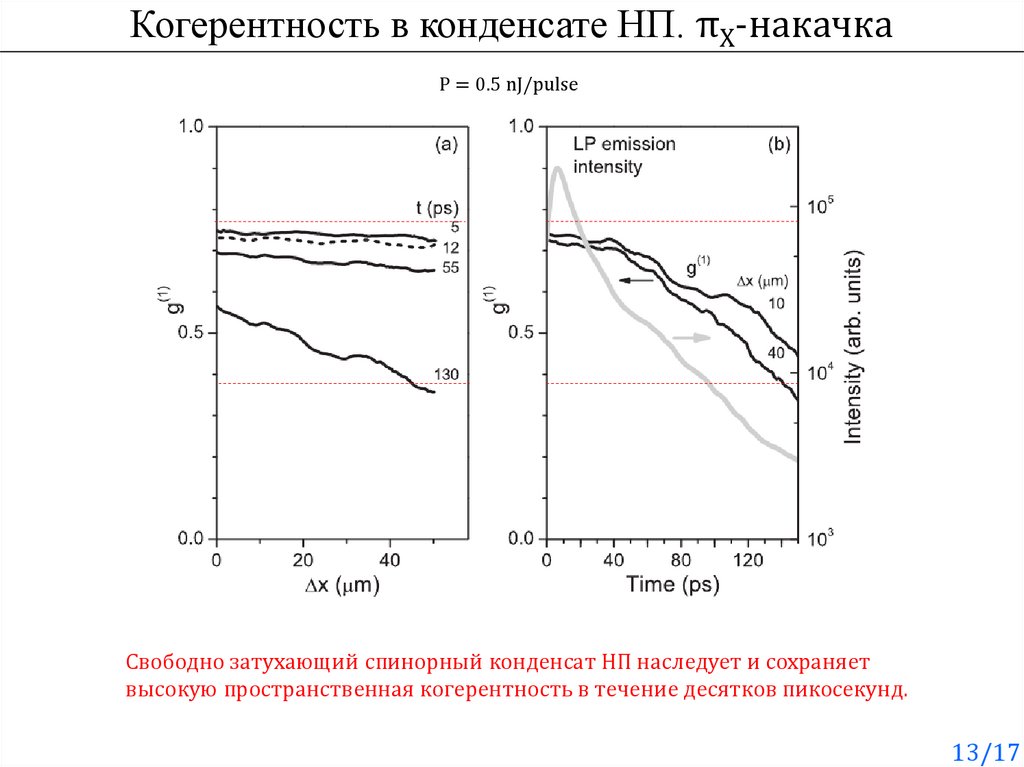
Когерентность в конденсате НП. πX-накачкаP = 0.5 nJ/pulse
Свободно затухающий спинорный конденсат НП наследует и сохраняет
высокую пространственная когерентность в течение десятков пикосекунд.
13/17
14.
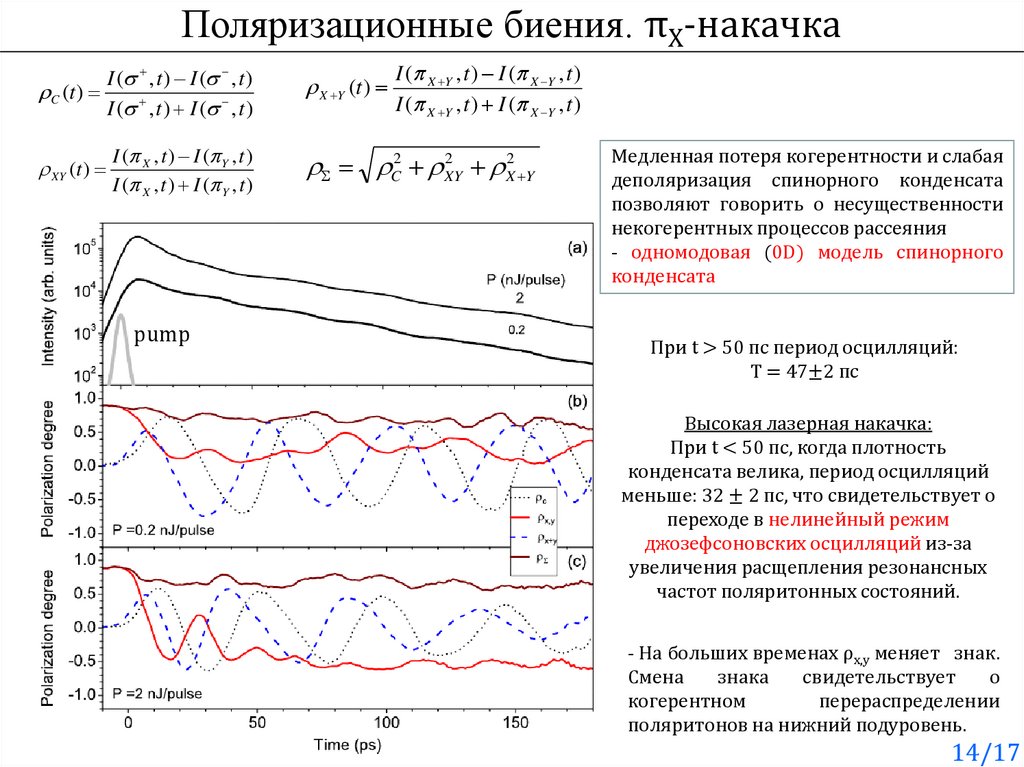
Поляризационные биения. πX-накачкаI ( , t ) I ( , t )
C (t )
I ( , t ) I ( , t )
XY (t )
I ( X , t ) I ( Y , t )
I ( X , t ) I ( Y , t )
pump
X Y (t )
I ( X Y , t ) I ( X Y , t )
I ( X Y , t ) I ( X Y , t )
2
C2 XY
X2 Y
Медленная потеря когерентности и слабая
деполяризация спинорного конденсата
позволяют говорить о несущественности
некогерентных процессов рассеяния
- одномодовая (0D) модель спинорного
конденсата
При t > 50 пс период осцилляций:
T = 47±2 пс
Высокая лазерная накачка:
При t < 50 пс, когда плотность
конденсата велика, период осцилляций
меньше: 32 ± 2 пс, что свидетельствует о
переходе в нелинейный режим
джозефсоновских осцилляций из-за
увеличения расщепления резонансных
частот поляритонных состояний.
- На больших временах ρx,y меняет знак.
Смена
знака
свидетельствует
о
когерентном
перераспределении
поляритонов на нижний подуровень.
14/17
15.
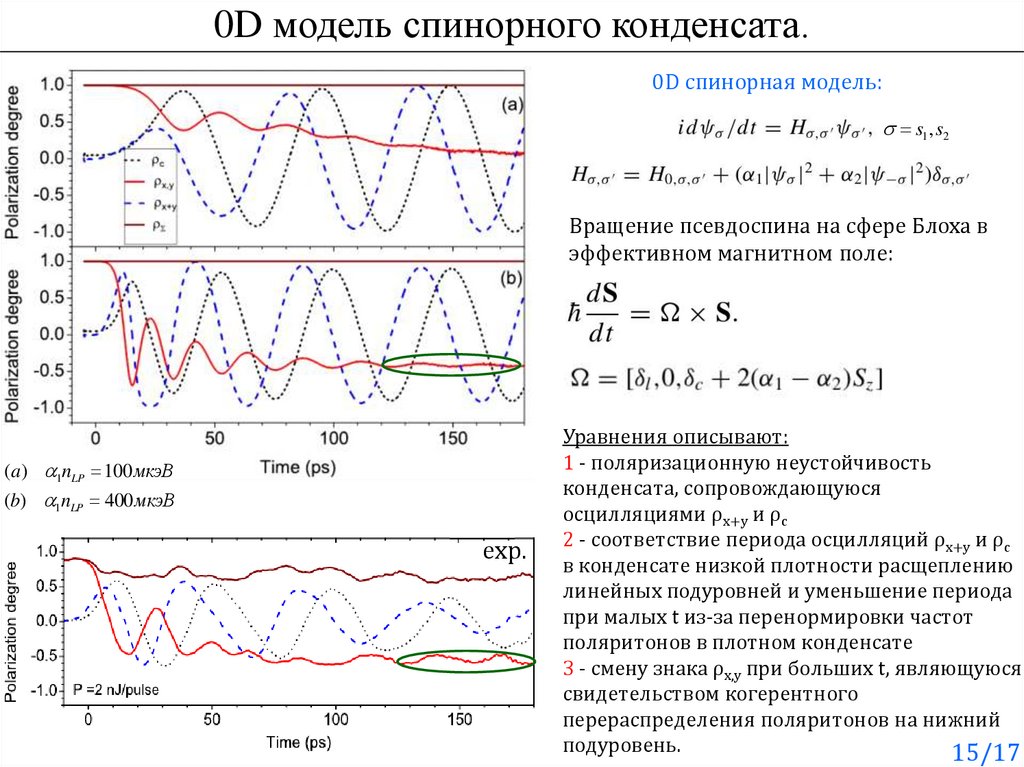
0D модель спинорного конденсата.0D спинорная модель:
s1, s2
Вращение псевдоспина на сфере Блоха в
эффективном магнитном поле:
(a) 1nLP 100 мкэВ
(b) 1nLP 400 мкэВ
exp.
Уравнения описывают:
1 - поляризационную неустойчивость
конденсата, сопровождающуюся
осцилляциями ρx+y и ρc
2 - соответствие периода осцилляций ρx+y и ρc
в конденсате низкой плотности расщеплению
линейных подуровней и уменьшение периода
при малых t из-за перенормировки частот
поляритонов в плотном конденсате
3 - смену знака ρx,y при больших t, являющуюся
свидетельством когерентного
перераспределения поляритонов на нижний
подуровень.
15/17
16.
Когерентное перераспределение поляритонов на нижний подуровеньХимпотенциал в поляритонной системе:
dE dn
E E
T
(t 0) 1 2 C2 S 0
Без затухания: nLP =const
2S0
; nLP 2S0
С затуханием: τLP =20 пс
α1nLP = 400 мкэВ
С
неравенство αl и α2 ведет к
зависимости
химпотенциала
конденсата от степени циркулярной
поляризации
(ρc)
даже
при
постоянной плотности: µ минимален
при
линейной
поляризации
конденсата и растет с ростом ρc.
В затухающем конденсате дефицит энергии,
возникающий
при
исчезновении
из
конденсата
частицы
с
эллиптической
поляризацией, компенсируется заменой части
компоненты
c
верхнего
подуровня
компонентой с нижнего подуровня с
сохранением когерентности конденсата.
16/17
17.
Выводы. Накачка в верхний отщепленный подуровень πXПри резонансном возбуждении верхнего отщепленного линейного
подуровня:
-конденсат наследует и сохраняет в течение десятков пикосекунд
когерентность лазерного импульса в широком диапазоне плотностей
возбуждения.
-конденсат теряет устойчивость при плотностях выше некоторого
порогового значения: он переходит в режим внутренних
джозефсоновских колебаний с сильно осциллирующими циркулярной
и диагональной линейной степенями поляризации. Причина:
спиновая анизотропия поляритон-поляритонного взаимодействия.
-наблюдается когерентное перераспределение поляритонов на
нижний подуровень. Причина: спиновая анизотропия поляритонполяритонного взаимодействия.
-при больших плотностях конденсата поляритон-поляритонное
взаимодействие приводит к “нелинейному” эффекту Джозефсона.
-эффекты хорошо описываются в рамках спинорных уравнений
Гросса−Питаевского.
17/17
18.
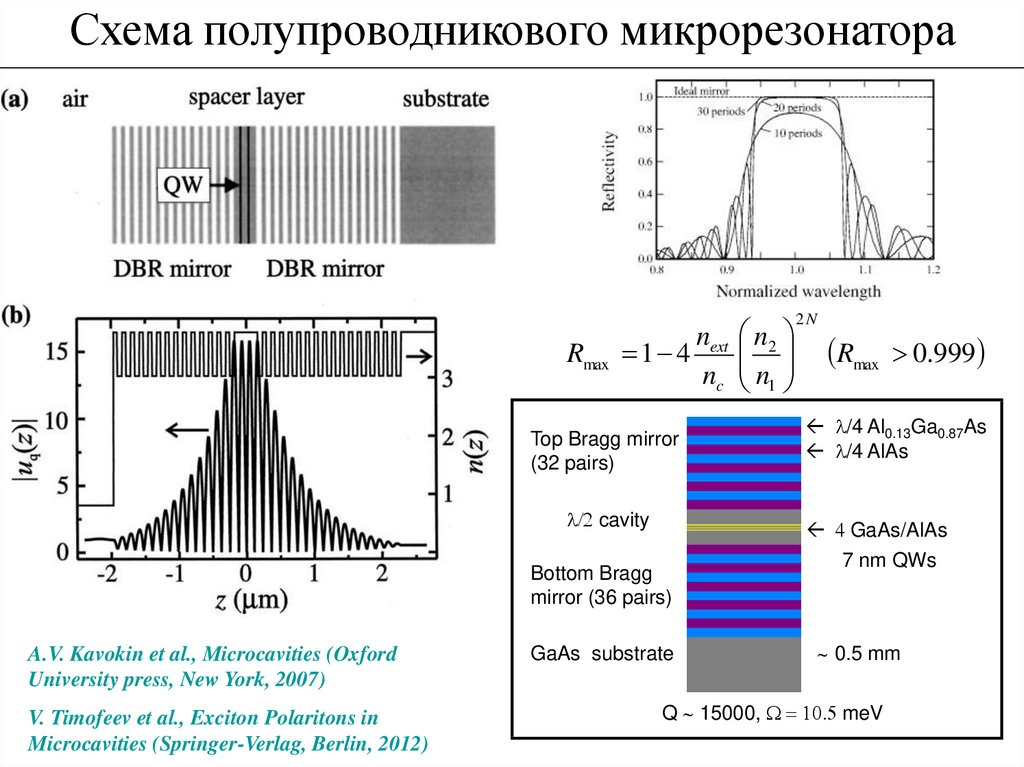
Спасибо за внимание!19. Схема полупроводникового микрорезонатора
Rmaxn
1 4 ext
nc
Top Bragg mirror
(32 pairs)
/2 cavity
Bottom Bragg
mirror (36 pairs)
A.V. Kavokin et al., Microcavities (Oxford
University press, New York, 2007)
V. Timofeev et al., Exciton Polaritons in
Microcavities (Springer-Verlag, Berlin, 2012)
GaAs substrate
n2
n1
2N
Rmax
0.999
/4 Al0.13Ga0.87As
/4 AlAs
4 GaAs/AlAs
7 nm QWs
~ 0.5 mm
Q ~ 15000, W 10.5 meV





 physics
physics








