Similar presentations:
Химическая физика горения
1. ХИМИЧЕСКАЯ ФИЗИКА ГОРЕНИЯ
ЛЕКЦИИНГУ 2012 г.
2. Программа курса
• Вводная лекция. История изучения процессов горения исовременное состояние исследований.
• Термодинамика процессов горения, температура и химический
состав системы в равновесии.
• Химическая кинетика. Скорость химических реакций.
Элементарные химические реакции, теория переходного
состояния. Кинетика обратимых, параллельных,
последовательных и цепных реакций.
• Роль диффузии и теплопередачи в процессах горения.
• Основы и математическое описание теории горения.
Самовоспламенение и зажигание. Теория теплового взрыва
Семенова и Франк-Каменецкого. Цепной взрыв.
• Теория распространения пламени в газах. Тепловая теория
Малляра–Ле-Шателье, Зельдовича–Франк-Каменецкого. Теория
цепного распространения пламени Зельдовича. Пределы
распространения пламени. Поджигание пламени искрой.
3. Программа курса
• Численное моделирование многокомпонентных реагирующих газовыхпотоков с применением многостадийных механизмов реакций и детальной
кинетики для описания скорости распространения и структуры
ламинарных пламен с помощью пакета CHEMKIN. Определение
лимитирующих стадий процесса и характерных путей реакций.
• Экспериментальные методы изучения горения газовых пламен.
• Измерение нормальной скорости распространения пламен.
• Измерение структуры пламен – профили концентрации веществ и
температуры в волне горения.
• Методы управления процессом горения - ингибирование и
промотирование горения.
• Ламинарные диффузионные пламена.
• Образование вредных веществ при горении, методы уменьшения их
выбросов.
• Горение конденсированных систем, экспериментальные методы
исследования.
• Исследование кинетики термического разложения конденсированных
веществ как первичного этапа процесса их горения.
• Горение энергетических материалов.
4.
Литература.1. Коробейничев О.П. Физика и химия горения: Учебное пособие / НГУ,
Новосибирск, 2011
2. Фристром Р.М., Вестенберг А.А. Структура пламени. М.: Металлургия,
1969.
3. Fristrom, R.M., Flame Structure and Processes. Oxford University Press,
New York, 1995.
4. Варнатц Ю., Маас У. и Диббл Р. «Горение. Физические и химические
аспекты, моделирование, эксперименты, образование загрязняющих
веществ». Москва. Физматлит. 2003
5. Kuo K.K. Principles of Combustion. A Wiley-Interscience. Publication, 1986.
6. Термодинамические свойства индивидуальных веществ. Справочник.
Под редакцией В.П. Глушко., М., Изд-во АН СССР, т. 1, т. 2, (1962)
7. JANAF Thermochemical Fables. (Stull D.R. Prophet- eds.). US Departament
of Commerce, Washington DC (1971)
8. Щетинков Е.С. Физика горения газов. М.: Наука, 1965.
9. Франк-Каменецкий Д.А. Диффузия и теплопередача в химической
кинетике. М.: Наука, 1967, 1987.
10. Зельдович Я.Б., Барнеблатт Г.И., Либрович В.Б. и Махвиладзе Г.М.
Математическая теория горения и взрыва. М.: Наука, 1980.
5.
Горение – это сложный физико-химическийпроцесс, при котором превращение
вещества сопровождается интенсивным
выделением тепла, ярким свечением и
тепломассообменом с окружающей средой.
6. ИСТОРИЯ РАЗВИТИЯ ЗНАНИЙ О ГОРЕНИИ
• люди началипользоваться огнем для
обогрева и
приготовления пищи
600 тысяч лет назад
• получать огонь – 30
тысяч лет назад
7.
Порох – Китай, Япония - IX век8. Огню отводилось значительное место в ранних мифах и легендах, например, в греческом мифе о Прометее, похитившем огонь у богов и
отдавшем его людям.9.
Огонь — наиболее динамичная,изменчивая из всех стихий,
первоначало мира, в то время
как вода — лишь одно из его
состояний.
Огонь сгущается в воздух, воздух
превращается в воду, вода — в
землю («путь вниз», который
сменяется «путём вверх»). Сама
Земля, на которой мы живём,
была некогда раскалённой частью
всеобщего огня, но затем —
остыла.
Геракли́т Эфе́сский
(544—483 гг. до н. э) —
древнегреческий
философ-досократик
10.
Одна из первых теорий,объясняющих
сущность
процесса горения - теория
флогистона. Иоганн Иоахим
Бехер, 1703 г
Процесс горения
заключается в разложении
вещества на флогистон и
остаток – землю.
11. Роберт Бойль считал, что при нагревании металлов «огненная материя» соединяется с металлами и превращает их в окалину. Так как
вес окалиныбольше веса металла, из
которого она получена, то,
по
мнению
Бойля,
флогистон имеет вес.
Роберт Бойль
(1627-1691)
12. Ломоносов М.В. 1711-1765
Закон сохранениямассы вещества
(Ломоносов -1756 г,
Лавуазье - 1773 г).
Ломоносов М.В.
1711-1765
Антуа́н Лора́н Лавуазье́
1743-1794
13. Майкл Фарадей 1791 - 1867
История свечи (1861)Майкл Фарадей
1791 - 1867
14. Ро́берт Ха́тчингс Го́ддард (1882—1945 ) один из пионеров современной ракетной техники
Эра жидкостных ракетных двигателей - 1926Ро́берт Ха́тчингс Го́ддард
(1882—1945 ) один из пионеров
современной ракетной техники
15. Разработка в России ракет ГИРД-9 и ГИРД-10, первый запуск 17 августа 1933г
Королев С.П.1907-1966
Тихонра́вов М.К.
1900-1974
16. Никола́й Никола́евич Семёнов (1896-1986), единственный советский лауреат Нобелевской премии по химии (получил в 1956 году
Открытие Семеновым Н.Н. в 1928 г цепныхразветвленных
реакций,
играющих
определяющую роль в горении и взрыве.
Никола́й
Никола́евич
Семёнов
(1896-1986),
единственный
советский лауреат Нобелевской
премии по химии (получил в 1956
году
совместно
с
Сирилом
Хиншелвудом)
17. Зельдо́вич Я́ков Бори́сович (1914-1987)
Теория распространения пламени• Установление связи между скоростью
распространения пламени и кинетикой
химических реакций
• Условия поджигания смеси
накаленной поверхностью,
определение фронта распространения
пламени и др.
• Механизм химич. реакции в
детонационной волне,
обосновывающий расчет скорости и
давления детонации.
Зельдо́вич Я́ ков Бори́сович
(1914-1987)
18. Основные области применения горения
• Тепловые электростанции на горенииугля, жидкого топлива.
• Печи для получения стали, цветных
металлов, стекла, керамики, цемента,
сажи углерода.
• Двигатели для автомобилей, самолетов,
ракет, судов.
• Артиллерия, стрелковое оружие и
другое вооружение.
• Взрывные работы.
• Уничтожение мусора, отходов, вредных
веществ.
19.
• В настоящее время горение является основнымисточником энергии.
• Более 85% потребляемой энергии в мире имеет
своим источником горение, большинство
современных технологий основано на
использовании горения.
• Количественное описание этого явления
представляет не только чисто научный интерес,
но также имеет большое практическое значение.
20.
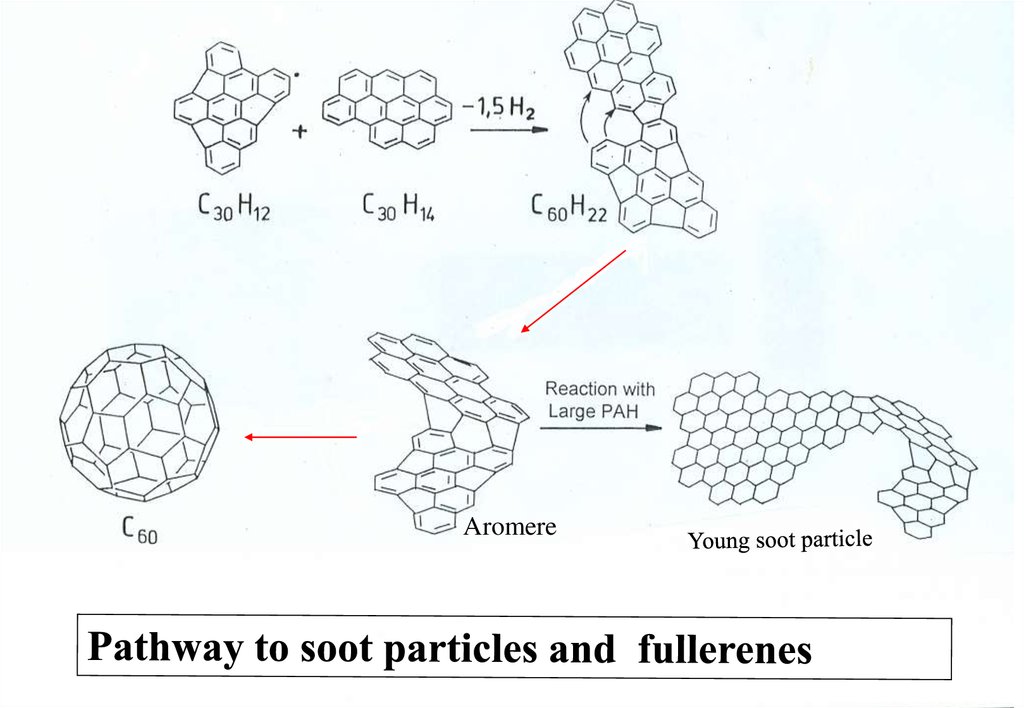
Formation of Flame Ions, Cluster, Nanotubes and Soot inHydrocarbon-Flames
.
H. Jander, H.Gg. Wagner
Institut für Physikalische Chemie der Universität
Tammannstr. 6, 37077 Göttingen, Germany
21.
.Aromere
22.
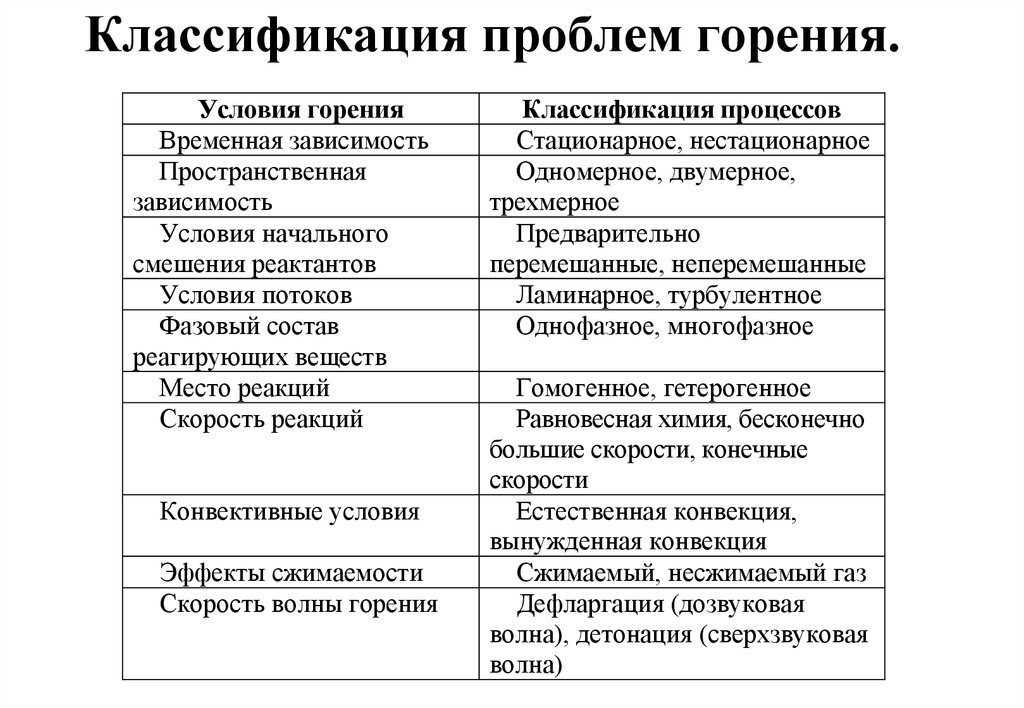
.23. Классификация проблем горения.
Условия горенияВременная зависимость
Пространственная
зависимость
Условия начального
смешения реактантов
Условия потоков
Фазовый состав
реагирующих веществ
Место реакций
Скорость реакций
Конвективные условия
Эффекты сжимаемости
Скорость волны горения
Классификация процессов
Стационарное, нестационарное
Одномерное, двумерное,
трехмерное
Предварительно
перемешанные, неперемешанные
Ламинарное, турбулентное
Однофазное, многофазное
Гомогенное, гетерогенное
Равновесная химия, бесконечно
большие скорости, конечные
скорости
Естественная конвекция,
вынужденная конвекция
Сжимаемый, несжимаемый газ
Дефларгация (дозвуковая
волна), детонация (сверхзвуковая
волна)
24. Процедуры разработки теоретической модели
1. Укажи общие цели модели2. Разработай физическую модель, основанную на понимании
главных механизмов и подходящих предположениях
(гипотезах)
3. Сконструируй главные рамки математической модели,
используя подходящие уравнения сохранения и транспорта
4. Проведи анализ порядков величин, чтобы упростить модель
5. Задай другие компоненты модели – начальные и граничные
условия, константы скорости, термодинамические и
транспортные свойства
6. Сделай математическую модель безразмерной,
идентифицируй безразмерные параметры .
7. Исследуй способность модели генерировать точное решение
для простых предельных случаев
8. Сравни теоретическое решение с экспериментом для
подтверждения модели
25. Основные соотношения в теории горения
Уравнение состояния для идеального - рV= nRT,где р – давление [Па], V – объем [м3], n – число молей [моль], T – температура
[К], R – универсальная газовая постоянная (R = 8,314 Дж/(моль K)).
Для смеси идеальных газов справедлив закон Дальтона:
1 N
p ni RT
V i 1
где N – полное число компонентов смеси
Сохранение масс. Химическую реакцию можно записать как
N
M
i 1
i
N
i
i
i M
i 1
где Мi – химический символ элемента, νi – стехиометрические
коэффициенты. Например, СО + 1/2О2 → СО2, здесь
М1 = CO, М2 = O2, М3 = CO2;
1 3 1; 2 1 / 2;
3 1 2 0.
26. Массовый баланс для одностадийной реакции
NW
.
i 1
i
i
N
i
i W
i 1
где Wi – молекулярный вес i-й компоненты смеси.
Определение долей реактантов
Массовая доля i-го реагента Yi с массой mi
причем
Yi 1.
i
Аналогично, мольная доля
mi
Yi
mi
i
Xi
ni
.
ni
i
Топливо-окислитель отношение
масса топлива
F /O
.
масса окислителя
Стехиометрический коэффициент (equivalence ratio)
F /O
( F / O ) st
27. индекс st соответствует стехиометрической реакции, например: CH4 + 2O2 → CO2 + 2H2O. Для бедных топливом смесей < 1; для
индекс st соответствует стехиометрической реакции,например:
CH4 + 2O2 → CO2 + 2H2O.
Для бедных топливом смесей < 1;
для стехиометрических смесей = 1
для богатых топливом
> 1.
Стандартная теплота образования
H
0
f
[ккал/моль] теплота, необходимая, чтобы один моль
вещества был образован из элементов при
стандартных условиях (Т = 298,16 К, Р = 1 атм);
.индекс f означает образование из элементов,
Надстрочный индекс “0” означает стандартные
условия
28. СТАНДАРТНЫЕ ТЕПЛОТЫ ОБРАЗОВАНИЯ ВЕЩЕСТВ
ВеществоАтом кислорода О (г)
Окись азота NО (г)
Молекула кислорода О2 (г)
Двуокись азота NO2 (г)
Озон О3 (г)
Атом водорода Н (г)
Молекула водорода Н2 (г)
Вода Н2О (г)
Закись азота N2O(г)
Н2О (ж)
NH (г)
Радикал НО2 (г)
NH2 (г)
Перекись водорода Н2О2 (ж)
Аммиак NН3 (г)
Гидроксил ОН (г)
ΔНf0 ккал/моль
59,5
21,6
0
8,0
34,0
52,1
0
–57,8
19,5
–68,3
81,2
3,9
42,3
–44,7
–11,0
9,3
29. Теплота реакции
Рассмотрим реакциюM M
N
i 1
N
i
i
i 1
i
i
Теплота реакции при стандартных условиях при температуре Т0:
H r , T0 i H 0f ,M i i H 0f ,M i
i
(х)
i
Во многих случаях требуется определить ΔНr при некоторой
температуре T2 , если известна теплота реакции при температуре
Т1. В этом случае имеем два равновесных состояния (ΔН)А =
(ΔН) В. Таким образом, можно записать:
H исх. вещ. H r , T2 H прод. H r , T1
N
T2
i 1
T1
H исх. вещ. i c p , M i dT
N
T2
i 1
T1
H прод. i c p , M i dT
30.
NT2
N
T2
H r , T2 H r , T1 i c p, M dT i c p, M dT
i 1
i 1
i
(хх)
i
T1
T1
H r , T2 H r , T1 ( H T H T ) прод. ( H T H T ) исх. вещ
.
Используя (х), (хх), а также приняв р = 1 атм.,
2
1
2
Т1 = Т0 = 298,16 К и обозначив Т ≡ Т2, получим:
H r , T
0
0
i H f , M i i H f , M i
i
i
T2
N
c
i
i 1
H r , T
T1
p, Mi
dT
N
T2
i 1
T1
i c p , M i dT
или:
T
T
N
0
0
i H f ,M i c p , M i dT i H f ,M i c p , M i dT
i 1
T1
i 1
T1
N
1
31.
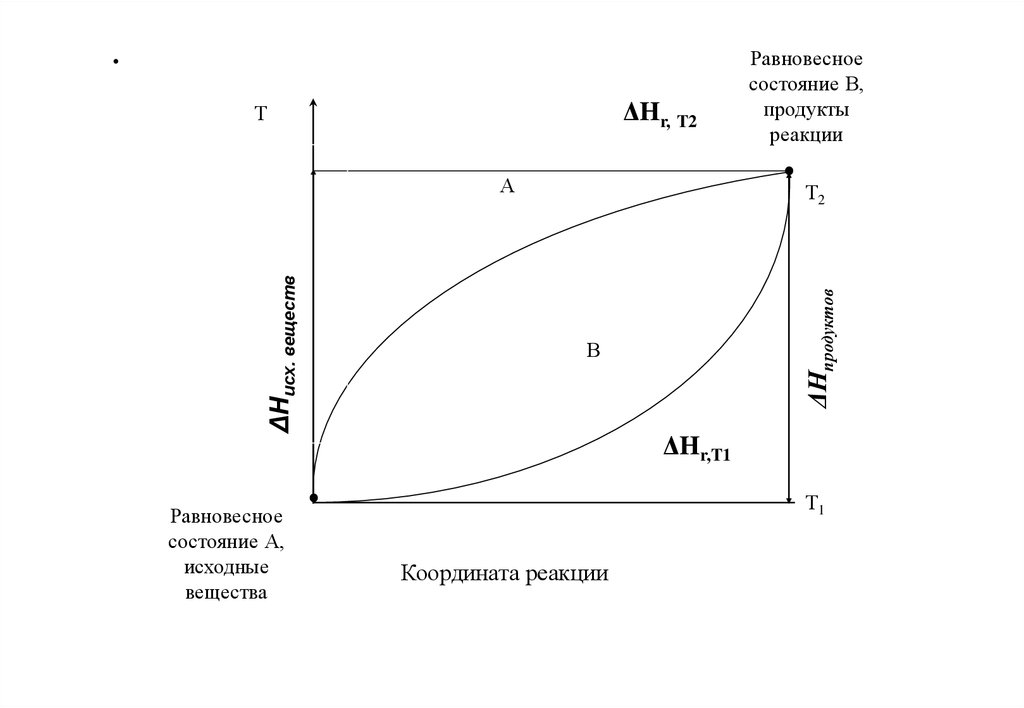
.ΔHr, T2
Т
Равновесное
состояние А,
исходные
вещества
Т2
ΔНпродуктов
ΔНисх. веществ
А
Равновесное
состояние В,
продукты
реакции
В
ΔHr,T1
Т1
Координата реакции
32.
Расчет адиабатической температуры пламениЕсли реагирующие вещества находятся при
температуре Ti, тогда баланс энергии примет вид:
N
H
j 1, прод.
N
0
H T0i H 00 H T00 H 00 H 0f T
j 1, исх. вещ.
N
H T0f H 00 H T00 H 00 H 0f T
0
C H T0 H 00 H T0 H 00
j 1
f
0
B H 0f T , j H 0f T , j
N
N
0
j 1
0
A H T0 H 00 H T0 H 00
j 1
j
j
j
N
j 1
i
0
H A B C
j
В адиабатическом процессе ΔН= 0
33.
Пример 1. Найти теплоту реакции окисления этана С2Н6.С2Н6 + 3,5O2 2CO2 + 3H2O.
ΔН = Σνi΄΄ΔHf Mi0 – Σνi΄ΔHf Mi0 = 2ΔHf CO20 + 3ΔHf H2O0 –
– ΔHf
C2H6
0–0
= –2 ∙ 94 – 3 ∙ 57,8 – (–20,24) = –341,16 ккал.
Пример 2. Определить адиабатическую температуру пламени
метановоздушной смеси состава: 1 моль метана + 15 молей воздуха
и концентрации продуктов без учета их диссоциации:
1 CH 4 15 0,21O2 0,79 N 2 1 CO2 2 H 2O( g ) 3 N 2 4 O2
34.
Решение. Уравнения сохранения элементов:С:
1 1 1 ;
O: 15(0,21∙2) = 2 1 2 2 4 ;
N: 15(0,79∙2) =
H:
3 ;
4 2 2
Решая эти уравнения, получим значения для 1 , 2 , 3 , 4 .
Адиабатическая температура пламени может быть
вычислена, с учетом того, что ΔН = 0, и следующего
уравнения:
35.
00
H i H f ,M i i H f ,M i i H Ti H T298
i
i
i
Mi
i H T f H T298
Mi
i
0.
Выражение в квадратных скобках есть ΔНr. Заметив, что
H T H T = 0, так как Ti = T298 и что H 0f = 0 для O2 и N2, получим
i
298
1 H
0
f , CO2
11,85 H
2 H 0f , H 2O( g ) 1 H 0f , CH 4 ( g ) 1 H T f H 298
2 H T f H 298
H 2O( g )
Tf
H 298
N2
CO2
1,15 H T f H 298
O2
= 0,
36.
ΔНr = 94,054 2 57,798 17,895 191,755 ккал .Предположим, что Тf = 2000 К и, используя данные из
таблиц, получим для второго члена
1 21901,89 СО2 2 17262 Н2О 11,85 13422 ,5 N2 1,15 14148 ,2 О2 231,753 ккал.
Предположив, что Тf = 1700 K, для второго члена
получим
1 17582 СО 2 13738 Н О 11,85 10861 N 1,15 11467 О 186,952 ккал.
2
2
2
2
Интерполируя, находим Тf = 1732 K.
37.
УЧЕТ ДИССОЦИАЦИИ ПРОДУКТОВ РЕАКЦИИПриведенный выше метод вычисления приемлем только, если Тf
< 1200 K. При более высоких температурах продукты реакции
диссоциируют и образуются другие соединения. Так, описанную
реакцию следовало бы заменить на
1 CH 4 15 0,21O2 0,79 N 2 1 CO 2 2 H 2O( g ) 3 N 2 4 O2 +
N
CO
NO
e
...
5 NO 6 H 7OH 8O + 9
10
11
12
В этом случае нужно к указанным выше уравнениям добавить
уравнения равновесия по реакциям, содержащие константы
равновесия.
N2 + O2 2NO
CO + ½O2 СО2
O2 2O
N2 2N
H2O ½H2+OH H2O H+OH
H2 2H
NO NO++ e-
38. Химический состав системы в равновесии
Рассмотрим обратимую реакцию:N
M
i 1
i
N
i
M
i
i
i 1
При условии, что все компоненты находятся в газообразном
состоянии, в состоянии равновесия при постоянном давлении можно
записать выражение для константы равновесия:
pi ,e
K P
i 1 p0
N
( i i' )
где pi,e – парциальное давление компонентов системы в равновесии,
p0 – общее давление в системе, p0= pi
39.
По определению, свободная энергия Гиббса:G ≡ H - TS
В химических процессах одновременно действуют два
противоположных фактора — энтропийный (TΔS) и энтальпийный (ΔH).
Суммарный эффект этих противоположных факторов в процессах,
протекающих при постоянном давлении и температуре, определяет
изменение энергии Гиббса (G):
ΔG = ΔH – TΔS
Если энергия Гиббса в исходном состоянии системы больше, чем в
конечном, то процесс принципиально может протекать (ΔG<0),
если наоборот (ΔG>0) — то не может.
Если ΔG=0,
равновесия.
то
система
находится
в
состоянии
химического
40.
Существует соотношение, связывающее изменение свободнойэнергии Гиббса в ходе химической реакции с её константой
равновесия:
GP0
K P exp(
)
RT
или
Gp0 RT ln K p
позволяющее находить состав системы в равновесии
41.
Пример 3. Рассмотрим реакцию окисления метана принедостатке кислорода
CH4+1.5O2=CO+2H2O,
которая благодаря реакции водяного газа
СО + Н2О = СО2 + Н2
идет по уравнению
СН4 + 1,5О2 (1 – )CO + (2 – )H2O + CO2 + H2.
Необходимо
найти
соотношения
для
нахождения
равновесного состава и определения адиабатической
температуры пламени.
42.
KPpCO2 pH 2
pCO pH 2O
nT ni (1 ) (2 ) 3
2
1
; X CO2 X H 2 ;
; X H 2O
3
3
3
2
1
; PCO2 / P PH 2 / P ;
; PH 2O / P
PCO / P
3
3
3
2
2
P
2
3
KP
2
1
1 2
P
P
3 3
f (KP ) f (KP (T ))
Тогда
X CO
(А)
43.
Для химической реакции в адиабатической системеCH4+1.5O2=(1- )CO+(2- )H2O+ CO2+ H2
Можно записать уравнение сохранения энтальпии
N
N
N
i 1
i 1
i 1
H i'' ( H 0f )i i' ( H 0f )i i'' H i
Tf
|
298
N
i' H i
i 1
298
|
Ti
0
44.
Это выражение можно переписать для индивидуальныхсоединений:
(1 ) H 0f ,CO (2 ) H 0f ,H2O H 0f ,CO2 H 0f ,CH 4 H 298 HTi
1.5 H 298 HTi
O2
(1 ) HT f H 298
HT f H 298
CO2
CO
(2 ) HT f H 298
HT f H 298
H2
0
H 2O
CH 4
(Б)
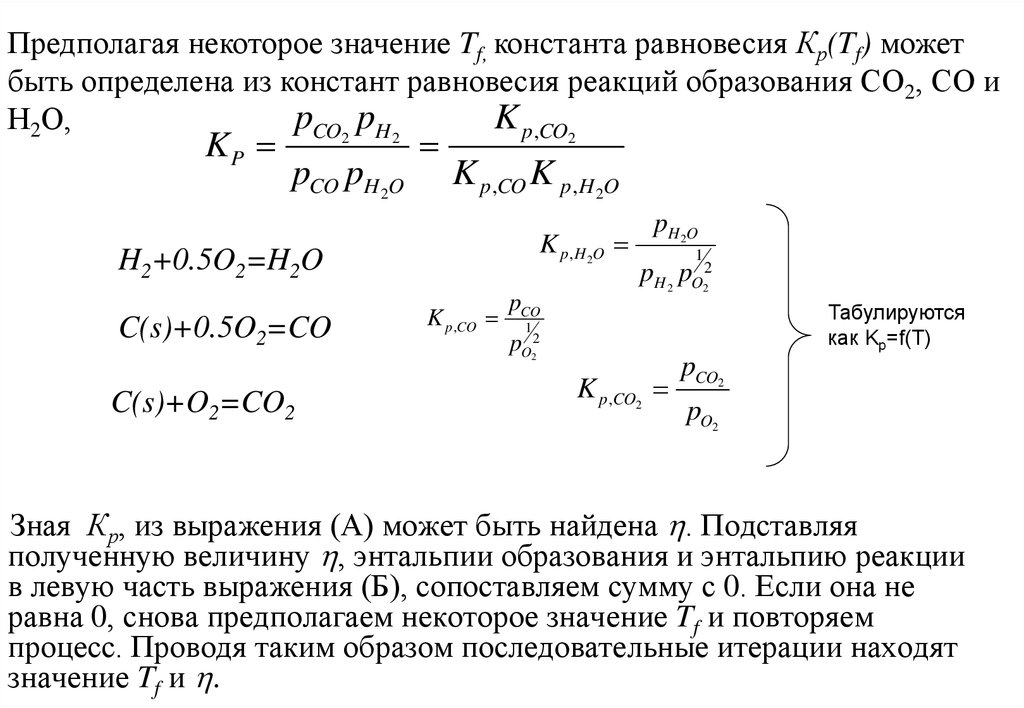
45.
Предполагая некоторое значение Tf, константа равновесия Кр(Tf) можетбыть определена из констант равновесия реакций образования СО2, СО и
pCO2 pH 2
K p ,CO2
Н2О,
KP
pCO pH 2O
K p ,CO K p ,H 2O
K p ,H 2O
H2+0.5O2=H2O
C(s)+0.5O2=CO
C(s)+O2=CO2
K p ,CO
pCO
pH 2O
1
pH 2 pO22
Табулируются
как Kp=f(T)
1
pO22
K p ,CO2
pCO2
pO2
Зная Кр, из выражения (А) может быть найдена . Подставляя
полученную величину , энтальпии образования и энтальпию реакции
в левую часть выражения (Б), сопоставляем сумму с 0. Если она не
равна 0, снова предполагаем некоторое значение Tf и повторяем
процесс. Проводя таким образом последовательные итерации находят
значение Tf и .



























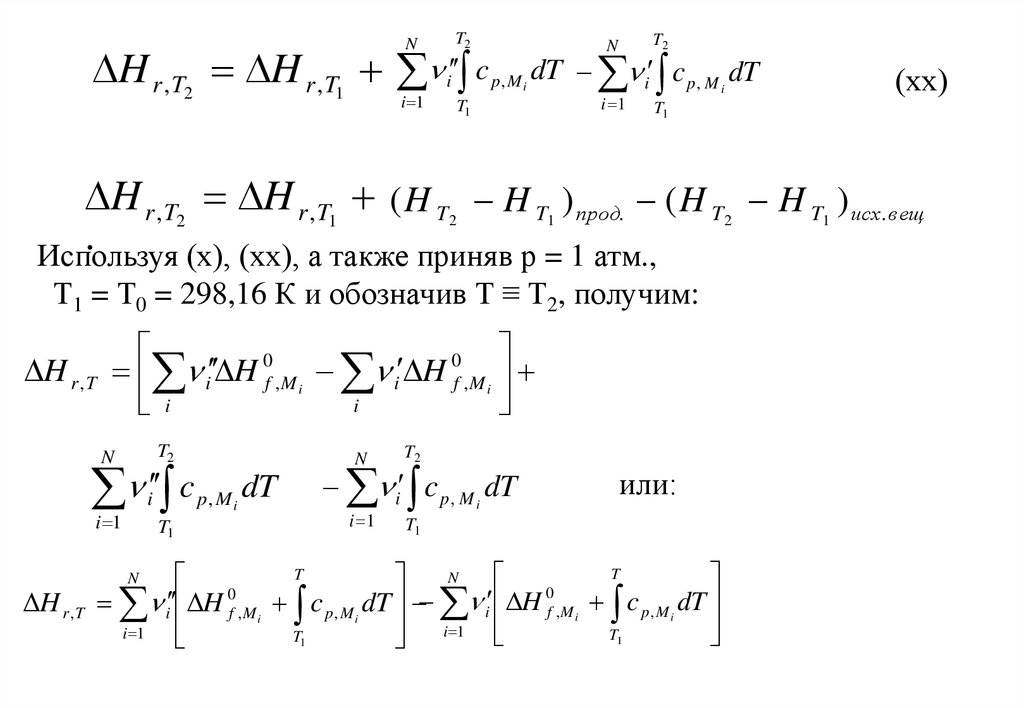



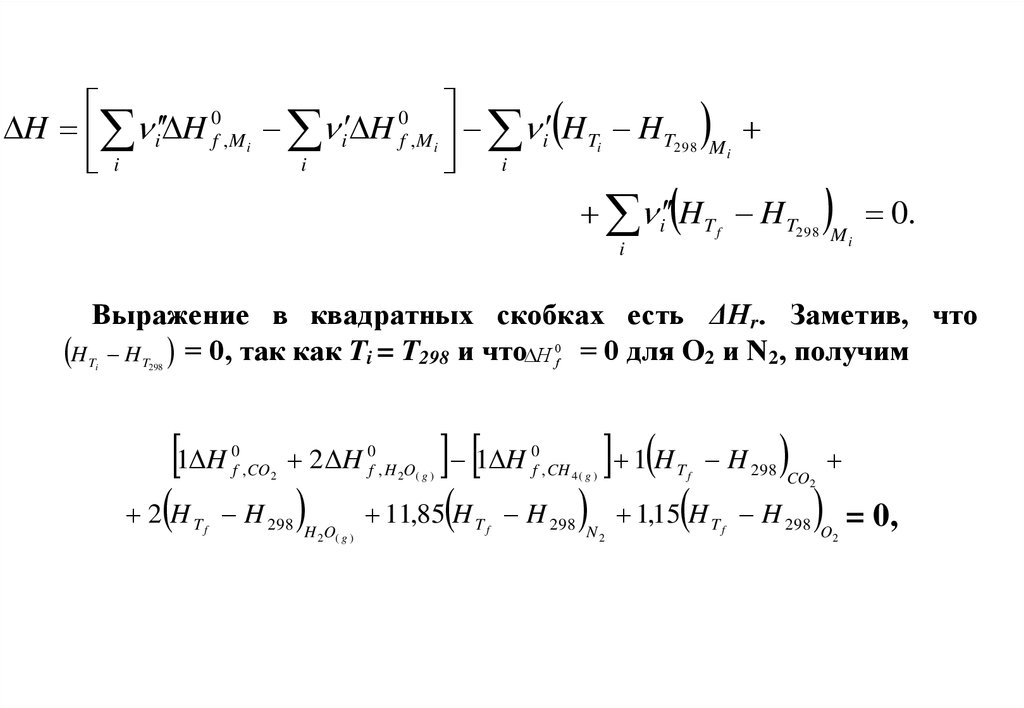









 chemistry
chemistry








