Төртұштықтардың кірістік, сипаттамалық кедергілері. Беріліс тұрақтысы. Таралу, өшу және фаза коэффициентері

1. Төртұштықтардың кірістік, сипаттамалық кедергілері. Беріліс тұрақтысы. Таралу, өшу және фаза коэффициентері. Пассивті

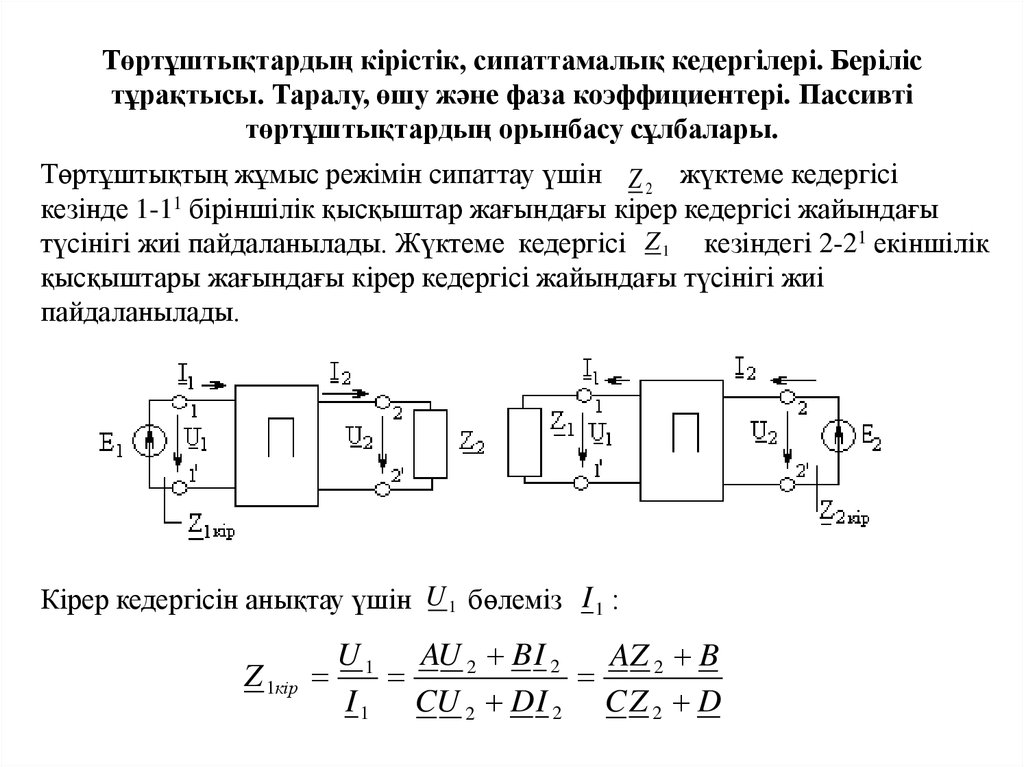
төртұштықтардың орынбасу сұлбалары.
Төртұштықтың жұмыс режімін сипаттау үшін Z 2 жүктеме кедергісі
кезінде 1-11 біріншілік қысқыштар жағындағы кірер кедергісі жайындағы
түсінігі жиі пайдаланылады. Жүктеме кедергісі Z 1 кезіндегі 2-21 екіншілік
қысқыштары жағындағы кірер кедергісі жайындағы түсінігі жиі
пайдаланылады.
Кірер кедергісін анықтау үшін U 1 бөлеміз I 1 :
Z 1кір
U 1 AU 2 B I 2
AZ 2 B
I 1 CU 2 D I 2 C Z 2 D

2.

Кірер кедергісі 2-21 қысқыштары жағынан:
Z 2 кір
U 2 DU 1 B I 1 D Z 1 B
I 2 CU 1 AI 1 C Z 1 A
Іс жүзінде Z 1кір және Z 2 кір үшін басқа да өрнектерді жиі пайдалануға
болады. Мысалы,
Z 1кір
B
B
Z
Z
2
1
Z 2к Z 2
Z Z1
A A
D D
Z 1б
Z 2 б 1к
, Z 2 кір
.
D
A
C
Z 2б Z 2
C
Z 1б Z 1
Z2
Z1
C
C

3.

Төртұштықтының сипаттамалық параметріне толқындық немесе
сипаттамалық кедергі және берілістің сипаттамалық түрақтысы жатады. Егер
төртұштықтылардың коэффициенттері бір-біріне тең болса A D , ол
төртұштықтылардың симметриялығын көрсетеді.
U 1 AU 2 B I 2
;
I 1 CU 2 D I 2
Егер төртұштықтының кірер кедергісі, толқындық кедергісіне тең болса,
онда төртұштық жүктемемен келісімді болып саналады. кедергісін
төртұштықтының сипаттамалық кедергісі дейміз. Сипаттамалық кедергі
қызметін толқындық кедергісі атқарады.
Z 1кір
U 1 AU 2 B I 2
AZ 2 B
I 1 CU 2 D I 2 C Z 2 D
, онда сипаттамалық кедергі:
ZC
AZ C B
.
CZ C D

4.

Z C C Z C D AZ C B,
B
.
C
Z C C Z C D AZ C B, Z C
2
Егер симметриялы төртұштықтының шыгар қысқыштарын кірмелік етіп, ал
кірерін – шықпалық етіп жасаса, онда сипаттамалық кедергі өзгермейді.
Егер төртұштық сипаттамалық кедергіге жүктелген болса:
U2
B
B
U 2 A BC ,
U 2 A
U 2 A
U 1 AU 2 B I 2 AU 2 B
ZC
ZC
B
C
I 1 CU 2 D I 2 C I 2 Z C D I 2 I 2 C Z C A I 2 A BC .
Кірердегі және шығардағы кернеулердің және токтардың қатынастары
бірдей:
U1 I1
U2
I2
A BC .
Егер бұл қатынас нақты болса, онда ол төртұштық арқылы энергия берілісі
кезінде кернеудің (және токтың) неше рет кемитінін көрсетеді. Яғни,
төртұштықтың өндіретін кернеуі (тоғы) әлсізденеді. Егер бұл қатынас
комплексті болса, онда модулі (өлшемі) - әлсізденуін анықтайды, ал
аргумент – фаза өзгерісін анықтайды.

5.

Көпшілік жағдайда кернеулердің және токтардың әлсізденуін, логарифмдік
бірлік бойынша өрнектейді, яғни кернеулердің және токтардың
қатынастарының натурал логарифмін анықтайды. Сондықтан
қабылдайтынымыз:
U1 I1
U
I
e g , g ln 1 ln 1 .
U2 I2
U2
I2
Мұндағы g екінші сипаттамалық параметр деп саналады және берілісті
сипаттамалық берілістің тұрақтысы немесе беріліс өлшемі дейміз. Бұдан
былай беріліс өлшемін, кернеулердің және токтардың қатынасы арқылы
емес, олардың көбейтінділерінің қатынастары арқылы көрсеткен дұрыс:
U1 I1
e2g
U2 I2
, сондықтан,
e g A BC , g ln A BC a jb
g
1 U1 I1
ln
2 U2 I2
беріліс тұрақтысы.

6.

- кернеудің және токтың абсолюттік мәнінің әлсіреуін көрсетеді де,
төртұштықтың сипаттамалық (өзіндік) өшуі немесе өшу тұрақтысы деп
аталады. Ол непермен өлшенеді. b - шамасы, кірердегі және шығардағы
кернеулердің (немесе токтардың) арасындағы фаза айырымына тең. Ол
сипаттамалық фаза немесе фазалық тұрақтысы деп аталады және радианмен
өлшенеді.
Пассивті төртұштықтылардың балама сұлбалары.
Пассивті төртұштықтарды баламалы Т-тәрізді және баламалы П-тәрізді
сұлбалар ретінде көрсетуге болады.
1. Т-тәрізді сұлба:
a
U 1 AU 2 B I 2
I 1 CU 2 D I 2
- А түріндегі теңдеулер.
U 1 U Z1 U Z 3 I 1 Z 1 I 2 Z 2 U 2
I1 I 3 I 2 I 2
Z U
(I 2 Z 2 U 2 )
Z
U
I 2 I 2 2 2 I 2 1 2 2 ;
Z3
Z3 Z3
Z3 Z3
Z
1
I1
U 2 I 2 1 2 CU 2 D I 2 ;
Z3
Z 3

7.

C және D
параметрлері: A 1 Z 1 ; B Z1 Z 2 Z 1 Z 2
Z
Z
3
3
Егер теңдеулердің коэффициенттері белгілі болса, Т-тәрізді сұлбаның
параметрлерін (кедергілерін) табамыз Z 1 , Z 2 , Z 3 , керісінше Т-тәрізді
сұлбаның параметрлері берілсе, теңдеулердің коэффициенттерін табамыз:
Z3
1
;
C
Z1
A 1
;
C
Z2
D 1
C
2. П-тәрізді сұлба:
U 1 AU 2 B I 2 ;
I1 CU 2 D I 2 ;
I3 I 2
U2
.
Z2
Z
U
U Z
U 1 U 2 I 3 Z 3 U 2 I 2 2 Z 3 U 2 I 2 Z 3 2 3 U 2 1 3 Z 3 I 2 AU 2 B I 2 .
Z2
Z2
Z2

8.

A және B :
I1
A 1
Z3
;
Z2
U1
U
U
I3 1 I2 2
Z1
Z1
Z2
B Z 3.
U2
Z
U2Z3
U 2 1 3 I 2 Z 3
I2Z3
U
Z2
Z2
I3
I2 2
Z1
Z1
Z2
Z
1
U 2 1 3
Z
Z
1
Z
I Z
Z3
1
2
2
I 2 1 3 CU 2 D I 2 .
I 2 2 3 U 2
Z1
Z1
Z1 Z1Z 2 Z 2 Z1
Z1
C және D параметрлері:
1
Z3
1
C
;
Z1 Z1Z 2 Z 2 Z1
Z3
D 1
;
Z1
Егер төртұштықтың коэффициенттері А,В,С,D берілген болса П-тәрізді
сұлбаның кедергілерін анықтауға болады: Z 3 B
B
B
Z2 B
Z
A 1
; A
; A Z2 Z 2 B; Z2 A 1 B.
2
A 1
Z2
Z2
D
Z1 B
;
Z1
D Z1 Z 1 B;
Z1
B
;
D 1