Similar presentations:
Układy logiczne
1. Układy logiczne
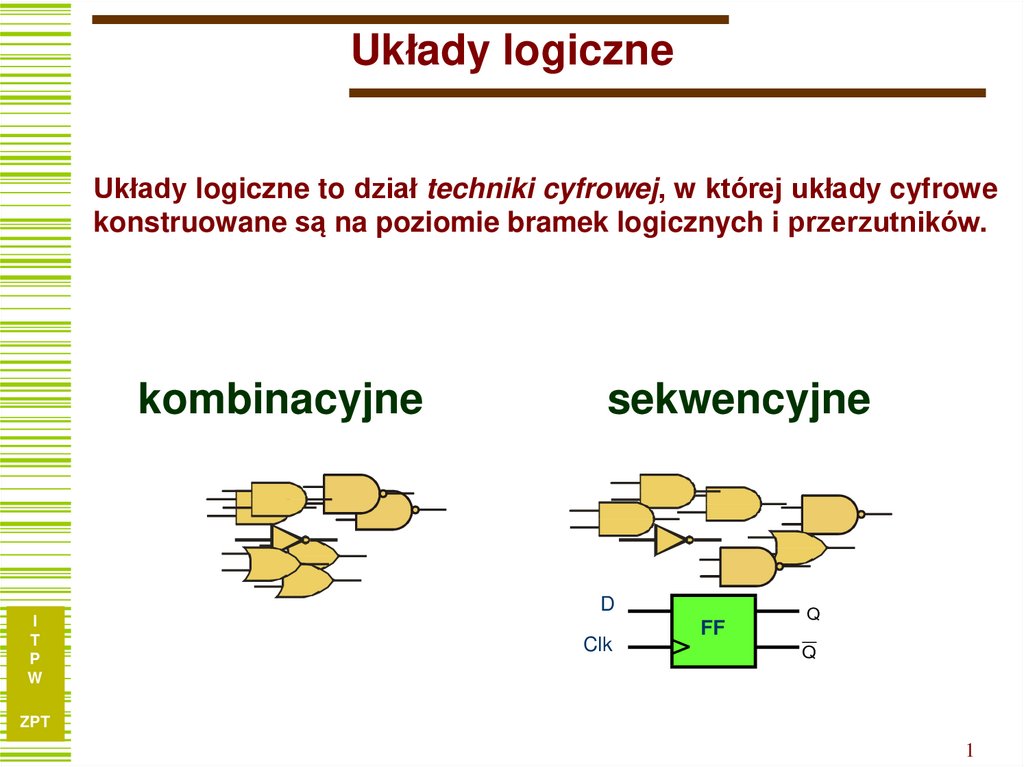
Układy logiczne to dział techniki cyfrowej, w której układy cyfrowekonstruowane są na poziomie bramek logicznych i przerzutników.
kombinacyjne
sekwencyjne
D
I
T
P
W
Clk
FF
Q
Q
ZPT
1
2. Slajd 2
Pojęcia podstawoweAlgebra Boole’a
…
I
T
P
W
ZPT
2
3. Slajd 3
Dwuelementowa algebra Boole’aAlgebra Boole’a jest modelem matematycznym operacji na sygnałach
binarnych reprezentujących sygnały elektryczne o dwóch wartościach: 0 lub
1. Wartości te są przyporządkowane dwom poziomom napięcia
wytwarzanego przez (elektroniczne) układy logiczne. Najczęściej przyjmuje
się, że napięciu wysokiemu jest przyporządkowana wartość sygnału 1,
natomiast napięciu niskiemu – wartość 0.
u(t)
Wysoki poziom = 5 V
Niski poziom = 0 V
Ciąg bitów .....
I
T
P
W
t
.... 0
1
0.....
ZPT
3
4. Slajd 4
Dwuelementowa algebra Boole’aAlgebra Boole’a jest algebrą z trzema operacjami na
dwuwartościowych argumentach, które przyjmują wartości: 0 i 1.
Rezultaty tych operacji są także dwuwartościowe.
Te trzy operacje to:
- suma logiczna (suma boolowska, alternatywa, lub),
- iloczyn logiczny (iloczyn boolowski, koniunkcja, i),
- negacja (inwersja, nie).
I
T
P
W
Dwie pierwsze operacje
jednoargumentowa.
są
wieloargumentowe,
a
trzecia
jest
ZPT
4
5. Slajd 5
Operacja sumy logicznej (OR)……jest zdefiniowana następująco: jeżeli co najmniej jeden z
argumentów jest równy 1, to wynik jest równy 1, zatem suma
logiczna jest równa 0 tylko dla przypadku, gdy wszystkie argumenty
są równe 0.
0+0=0
0+1=1
1+0=1
1+1=1
I
T
P
W
Bramka OR
a
b
c=a+b
gdzie + oznacza operację OR
ZPT
5
6. c = a • b
Operacja iloczynu logicznego (AND)……jest zdefiniowana następująco: wynik iloczynu jest równy 1, wtedy i
tylko wtedy, gdy wszystkie argumenty przyjmują wartość 1.
0•0=0
0•1=0
1•0=0
1•1=1
I
T
P
W
Bramka AND
a
b
c=a•b
gdzie • oznacza operację AND
ZPT
6
7. Slajd 7
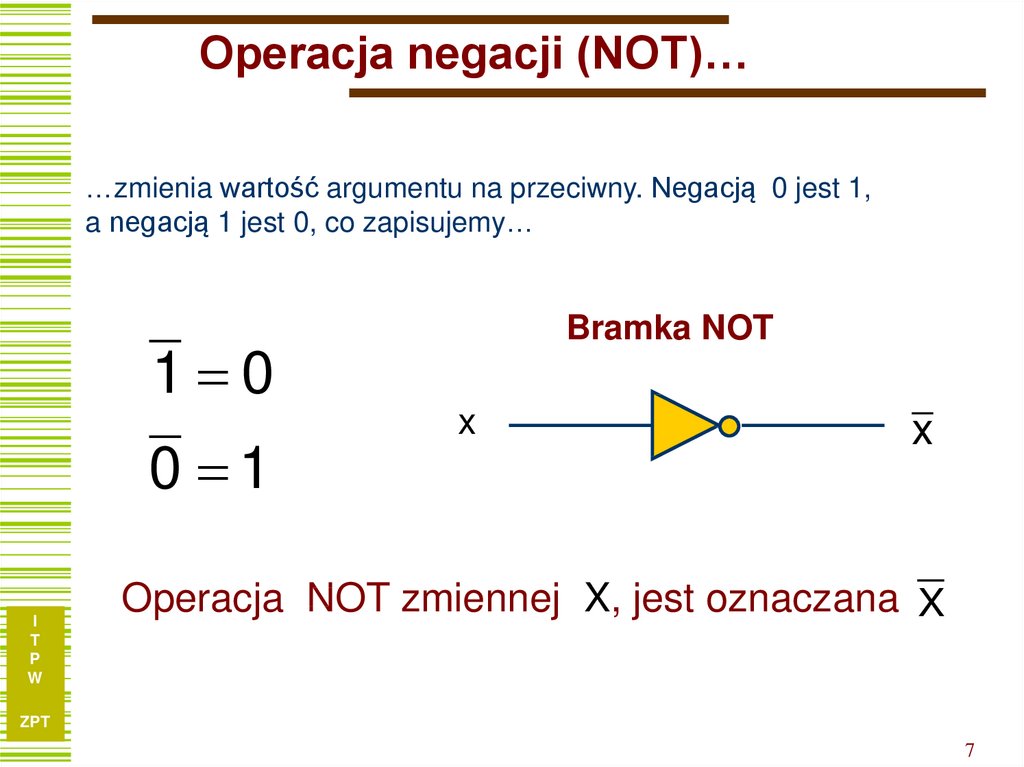
Operacja negacji (NOT)……zmienia wartość argumentu na przeciwny. Negacją 0 jest 1,
a negacją 1 jest 0, co zapisujemy…
Bramka NOT
1 0
0 1
I
T
P
W
x
x
Operacja NOT zmiennej X, jest oznaczana X
ZPT
7
8. Prawa i własności algebry Boole’a
Własności stałycha+0=a
a 0=0
a+1=1
a 1=a
a a 1
Własności negacji
a a 0
Podwójna negacja
a a
Idempotentność
a+a=a
a a=a
I
T
P
W
ZPT
8
9. Prawa i własności algebry Boole’a c.d.
Przemiennośća+b=b+a
a b=b a
Łączność
a + (b + c) = (a + b) + c
a (b c) = (a b) c
Rozdzielność
a + b c = (a + b) (a + c)
a (b + c) = a b +a c
Prawa De Morgana
y a b a b
y a b a b
I
T
P
W
ZPT
9
10. Wyrażenie boolowskie
Wyrażenie boolowskie to formuła, w której zmienneboolowskie połączone są operatorami: + (OR),
(AND), (NOT) X
Przykład:
a+b+c•d+e
a+b(d+e)
a+b+cd+e
Kropkę często pomijamy
Kolejność operacji:
I
T
P
W
ZPT
1. NOT
2. AND
3. OR
(Może być zmieniona przez stosowanie nawiasów).
10
11. Iloczyn kartezjański
Iloczynem kartezjańskim zbiorów A i B , oznaczanym A × Bnazywamy zbiór wszystkich par uporządkowanych (a, b), takich że
pierwszy element pary należy do zbioru A (a A), natomiast drugi
do B (b B).
A B a, b : a A, b B
Przykładzik
{0, 1}3
I
T
P
W
ZPT
000
001
011
010
110
111
101
100
11
12. Funkcja boolowska
Funkcją boolowską zmiennych binarnych x1,... ,xn nazywamyodwzorowanie:
f: X Y
gdzie:
X Bn = {0,1} {0,1} ... {0,1},
Y Bm
n-razy
Jeżeli X = B n, to funkcję nazywamy zupełną; w przeciwnym przypadku
jest to funkcja niezupełna, zwana również funkcją nie w pełni
określoną.
Reprezentacje:
I
T
P
W
ZPT
Tablica prawdy
Formuła (wyrażenie) boolowskie
... i wiele innych sposobów opisu (np. BDD)
12
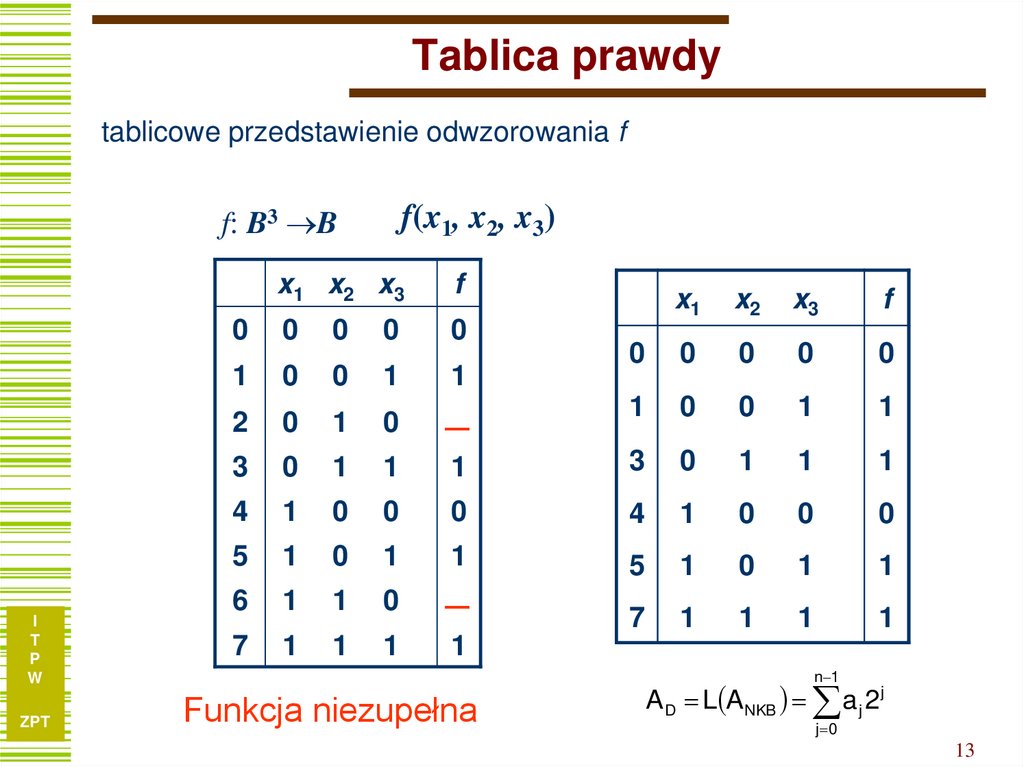
13. Tablica prawdy
tablicowe przedstawienie odwzorowania ff: B3 B
I
T
P
W
ZPT
f(x1, x2, x3)
x1 x2 x3
f
0
0
0
0
0
1
0
0
1
1
2
0
1
0
3
0
1
4
1
5
x1
x2
x3
f
0
0
0
0
0
1
0
0
1
1
1
0
─
1
3
0
1
1
1
0
0
0
4
1
0
0
0
1
0
1
1
5
1
0
1
1
6
1
1
0
1
─
7
1
1
1
1
7
1
1
1
1
n 1
Funkcja niezupełna
AD L ANKB a j 2 j
j 0
13
14. Tablica prawdy...
n 1A D L A NKB a j 2 j =
j 0
= an-1 2n-1 +....+ a2 22 + a1 21 + a0 20
(0101)B = 0 23 + 1 22 + 0 21 + 1 20 = 5D
(1010)B = 1 23 + 0 22 + 1 21 + 0 20 = 10D
I
T
P
W
ZPT
14
15. Uproszczony zapis tablicy prawdy
IT
P
W
x1
x2
x3
f
x1
x2
x3
f
0
0
0
0
0
0
0
0
0
0
1
0
0
1
1
1
0
0
1
1
2
0
1
0
0
2
0
1
0
─
3
0
1
1
1
3
0
1
1
1
4
1
0
0
0
4
1
0
0
0
5
1
0
1
1
5
1
0
1
1
6
1
1
0
1
6
1
1
0
─
7
1
1
1
1
7
1
1
1
1
f = (1, 3, 5, 6, 7)
f = [1, 3, 5, 7, (2, 6)]
ZPT
15
16. Wyrażenie boolowskie
Znacznie wygodniejsza w praktyce jestreprezentacja funkcji boolowskich w
postaci wyrażenia boolowskiego.
I
T
P
W
ZPT
16
17. Wyrażenie boolowskie - przykład
x1x2
x3
f
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
f x1x2x3 x1x2x3 x1x2x3 x1x2x3 x1x2x3
f x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3
I
T
P
W
Ogromne znaczenie formuł boolowskich ...
ZPT
17
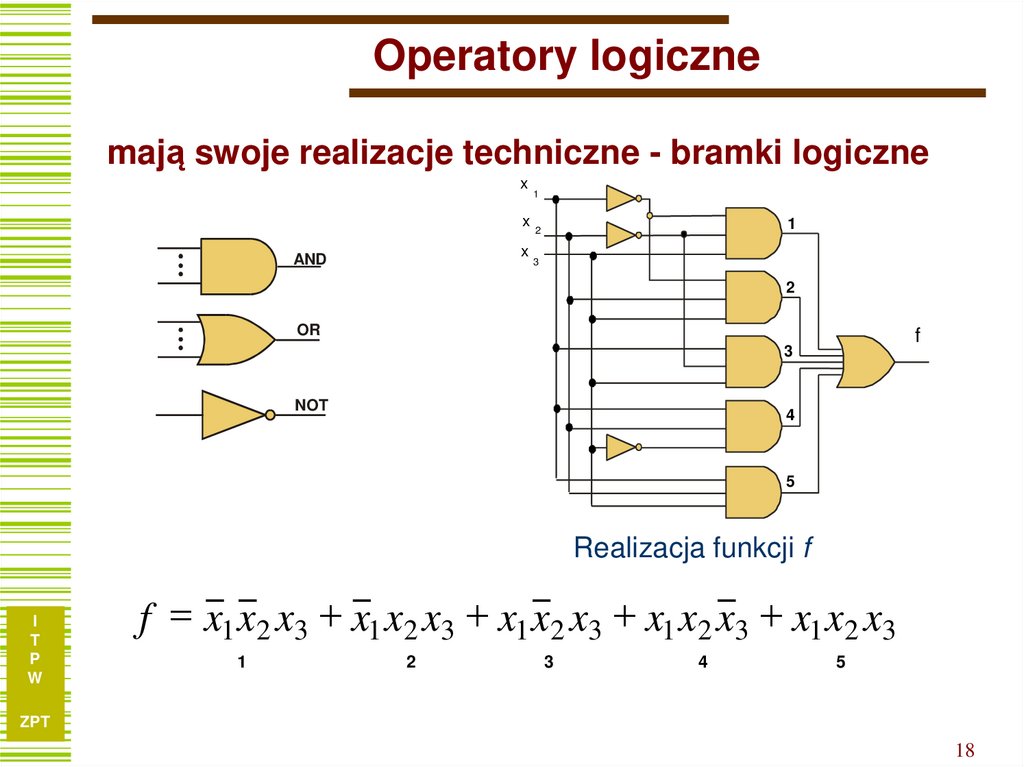
18. Operatory logiczne
mają swoje realizacje techniczne - bramki logicznex
x
x
AND
1
1
2
3
2
OR
f
3
NOT
4
5
Realizacja funkcji f
I
T
P
W
f x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3
1
2
3
4
5
ZPT
18
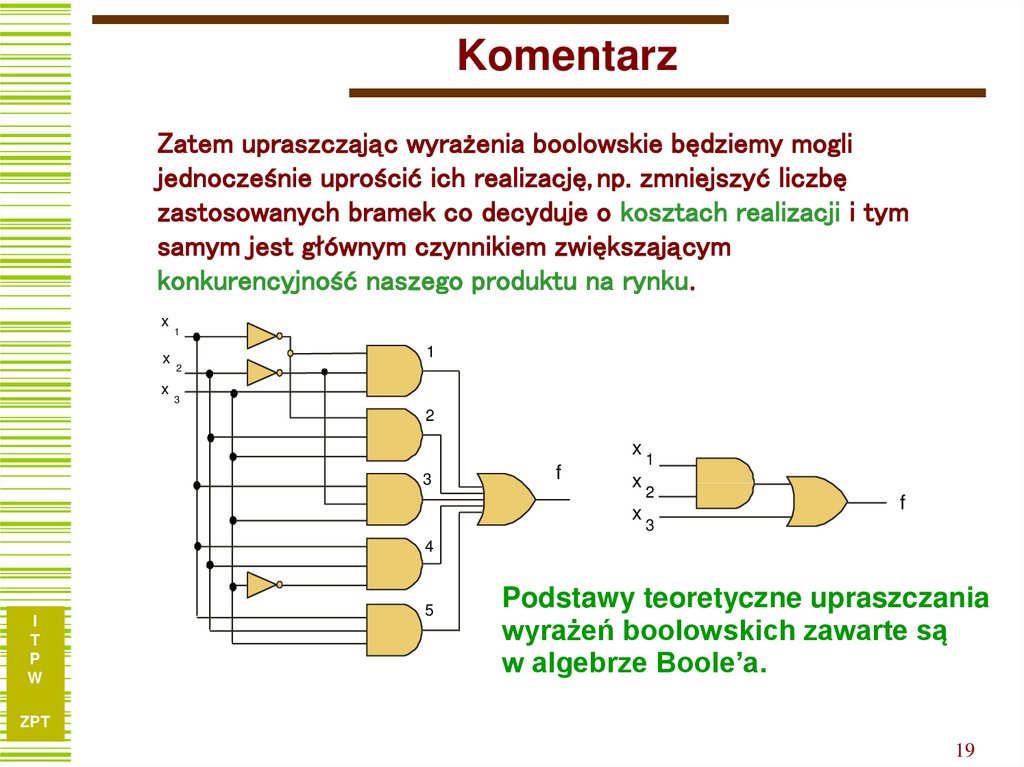
19. Komentarz
Zatem upraszczając wyrażenia boolowskie będziemy moglijednocześnie uprościć ich realizację, np. zmniejszyć liczbę
zastosowanych bramek co decyduje o kosztach realizacji i tym
samym jest głównym czynnikiem zwiększającym
konkurencyjność naszego produktu na rynku.
x
x
x
1
1
2
3
2
x
3
f
x
x
1
2
f
3
4
I
T
P
W
5
Podstawy teoretyczne upraszczania
wyrażeń boolowskich zawarte są
w algebrze Boole’a.
ZPT
19
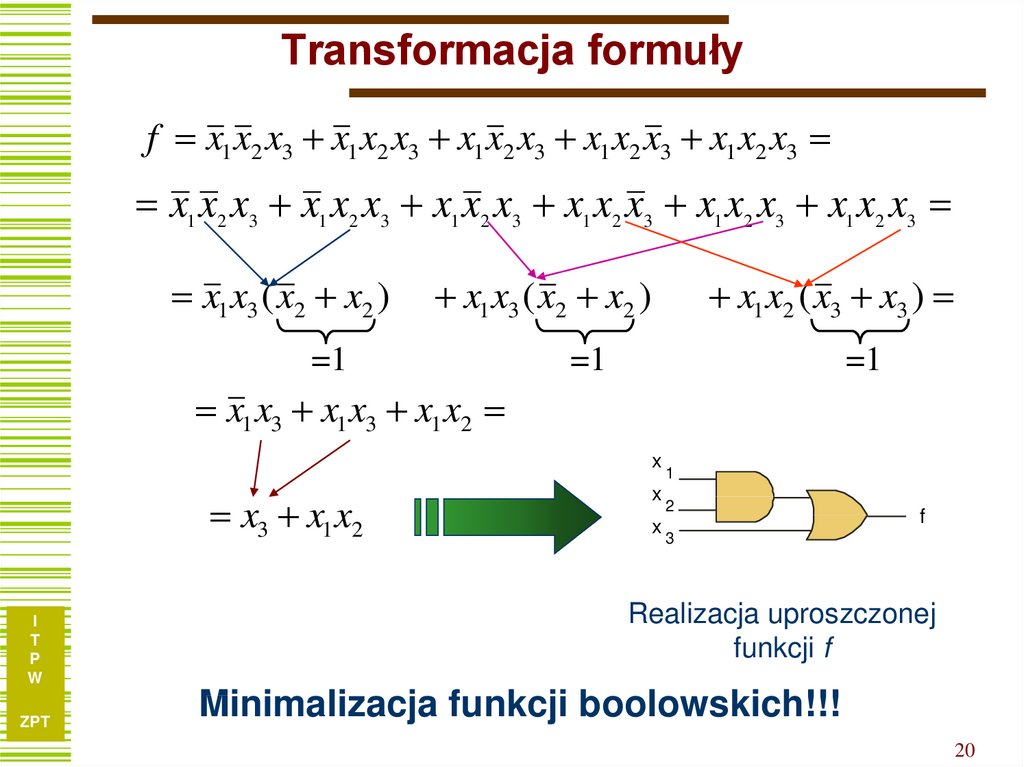
20. Transformacja formuły
f x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3 x1 x2 x3
x1 x3 ( x2 x2 )
x1 x3 ( x2 x2 )
=1
x1 x2 ( x3 x3 )
=1
=1
x1 x3 x1 x3 x1 x2
x
x3 x1 x2
I
T
P
W
ZPT
x
x
1
2
f
3
Realizacja uproszczonej
funkcji f
Minimalizacja funkcji boolowskich!!!
20
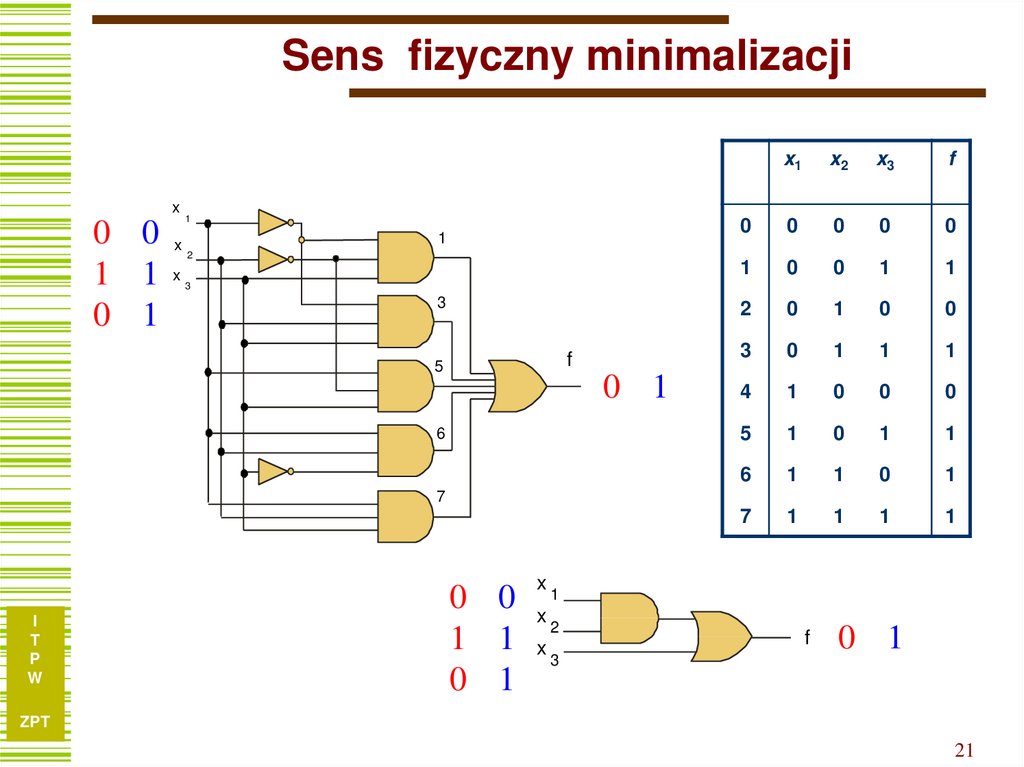
21. Sens fizyczny minimalizacji
x0 0
1 1
0 1
x
x
1
1
2
x1
x2
x3
f
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
3
3
f
5
0 1
6
7
I
T
P
W
0 0
1 1
0 1
x
x
x
1
2
3
f
0 1
ZPT
21
22. Postaci (formy) kanoniczne
Kanoniczna postać sumacyjna(suma iloczynów)
Kanoniczna postać iloczynowa
(iloczyn sum)
I
T
P
W
ZPT
22
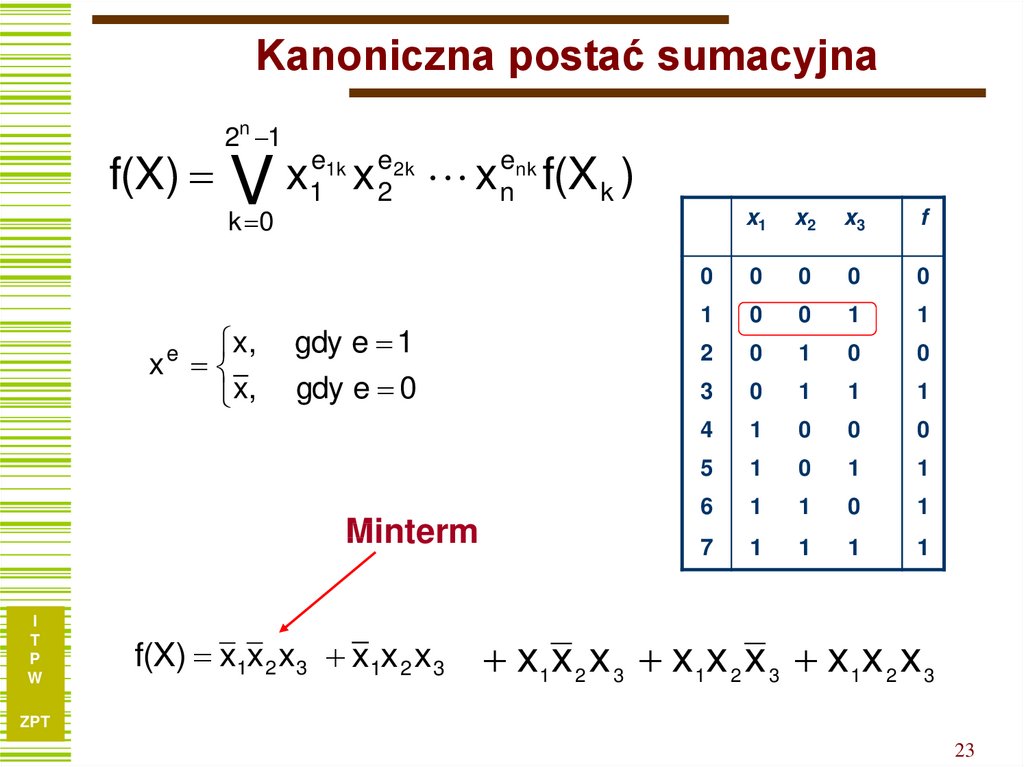
23. Kanoniczna postać sumacyjna
f(X)2n 1
Vx
k 0
x,
xe
x,
e1k
1
x
e 2k
2
x f(X k )
gdy e 1
gdy e 0
Minterm
I
T
P
W
f(X) x1x 2 x 3 x1x 2 x 3
enk
n
x1
x2
x3
f
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
x 1x 2 x 3 x 1x 2 x 3 x 1x 2 x 3
ZPT
23
24. Kanoniczna postać iloczynowa
f(X)x
2n 1
k 0
x,
e
x
x,
e1k
1
x e22k x nenk f(X k )
gdy e 0
gdy e 1
Maxterm
I
T
P
W
x1
x2
x3
f
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
f (x1 x 2 x 3 ) ( x1 x 2 x 3 ) ( x x x )
1
2
3
ZPT
24
















 mathematics
mathematics








